四自由度串联机器人用电磁作动器设计*

2022-04-12魏国莲李积元

传感器与微系统 2022年4期

魏国莲，李积元

(1.青海高等职业技术学院机电工程系，青海海东 810799； 2.青海大学机械工程学院，青海西宁 810500)

0 引言

目前，利用电磁原理的电磁作动器(electro-magnetic actuator，EMA)已被广泛应用于多种工程应用领域，证明了其准确性和可靠性[1～4]。除了常用的EMA技术外，近期人们开始尝试开发各种新型的作动器，用于解决某些复杂的工程问题。

例如，EMA已被用于作业空间有限的微型机器人应用[5,6]。Tehrani等人[7]研究了用于药物输送和治疗应用的微型机器人，以引导血管中的磁性纳米颗粒。该微型机器人由EMA驱动，可以完成微创手术等任务。Choi等人[8]开发了一种新型EMA，由该EMA驱动的微型机器人能够按照预定的轨迹在三维空间中移动。Li等人[9]还开发了一种梯度增强型EMA来精确驱动微型机器人移动到目标位置。Zou等人[10]提出了一种新颖的EMA并制造出受昆虫启发的扑翼机器人。这种微型机器人的重量为80 mg，翼展为3.5 cm，能够产生足够的推力起飞。但是，上述研究中的EMA均存在通用性较差的问题，仅适用于某些特殊场景的微型机器人应用，无法满足多样化应用的需求。

针对上述问题，本研究的主要贡献是提出了一种新颖的小型模块化双轴EMA，可适用于多种应用场景。所提EMA的模块化特性可以将多个作动器模块连接在一起，从而提供了更多潜在的应用。例如，如果串联多个模块可以用来生成蛇形机器人。如果以并联结构连接，则可以用来生成四足机器人。该机器人具有可操作性强、重量轻、体积小等特点。

1 双轴电磁作动器设计

1.1 模块设计

所提双轴EMA由两个垂直的框架(一个固定框架和一个移动框架)组成，并通过另一个自由移动框架连接在一起。该自由移动框架悬挂在两个轴上，允许绕x轴和y轴旋转。电磁线圈连接在固定和移动框架上。每个线圈大约有820匝，电阻为58 Ω。为了集中和保持线圈所产生的磁场，线圈内部安装了一个软铁轭。一个5 mm3的永磁体固定在自由移动框架中。在这项研究中使用了钕磁铁[11]，因为它是目前为止具有最强磁力的商业可用永磁体。在每个模块的两端使用另一个内置磁铁，以便与其他模块连接。单个双轴EMA模块如图1所示。

图1 单个双轴EMA模块

1.2 工作原理分析

单个EMA模块主要由两个正交方向的电磁线圈和一个固定在自由移动框架上的永磁体组成。通过驱动任意一个线圈，自由移动框架可围绕相应的轴旋转。所提EMA的驱动原理主要是利用载流线圈和永磁体产生洛伦兹力F。洛伦兹力产生的原理如图2所示。

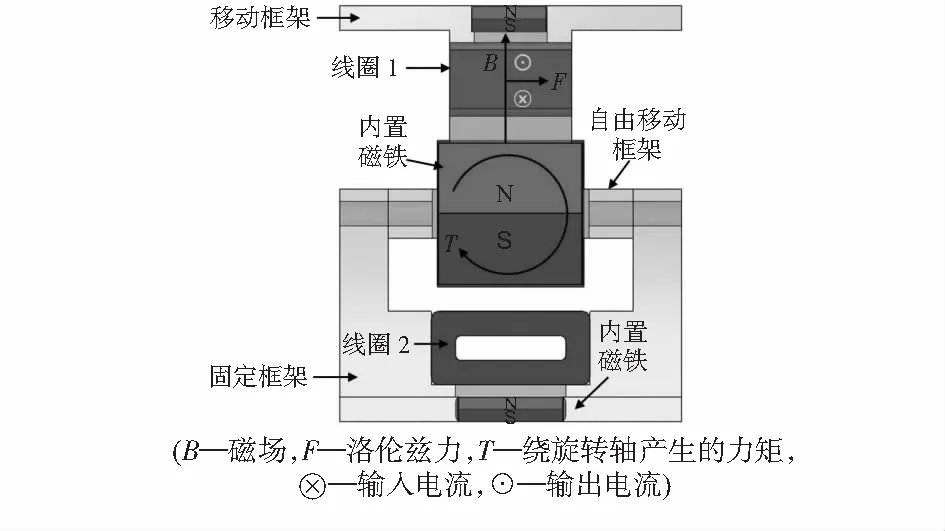
图2 洛伦兹力产生的原理

通过改变提供给线圈的电流方向，可以改变所产生洛伦兹力F的方向。因此，通过激励线圈1，自由移动框架绕轴Z0旋转。同样，通过激励线圈2，自由移动框架可以绕轴旋转。

EMA的动力学方程与文献[12]中直流电机的动力学方程相似。因此，作动器的动力学方程可以写成

J+Tm=Te

(1)

Tm=Kmθ

(2)

Te=KtI

(3)

V=RI+Ke

(4)

式中J为作动器的质量转动惯量;，和θ为角加速度、角速度和旋转角;Tm为将永磁体旋转到默认位置的恢复力矩;Te为基于线圈产生的磁场将永磁体旋转到一定角度的力矩;Km为恢复力矩常数;Kt为磁力矩常数;I为施加到线圈上的电流;V为施加的电压;R为线圈电阻;Ke为反电动势常熟。

旋转角度与施加电压的关系如下

(5)

所提EMA模型类似于直流电动机(即音圈电机)。直流电机的主要特点是输出力矩与施加的电流成正比，如式(3)所示。

1.3 特性分析

为了验证所开发作动器的性能，进行了有限元仿真和实测分析。单个EMA模块的有限元仿真结果如图3所示。

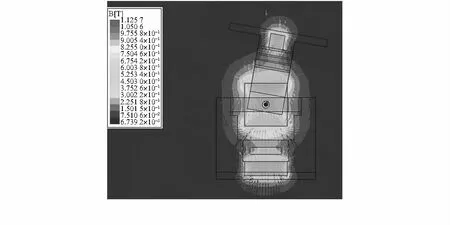
图3 单个EMA模块的有限元仿真结果

使用载荷传感器和激光传感器来测量力矩和旋转角。使用函数发生器来提供激活线圈所需的电流。产生的转矩结果如图4所示。

图4 相对于外加电流产生的转矩结果

仿真结果表明，该作动器可以达到100 mN·m的力矩。而实测表明，在相同的外加电流下，只能达到80 mN·m。此外，该作动器的旋转角可以达到10 °(≈0.2 rad)。仿真结果与实测结果之间的差异是由于机械误差和不同的材料性能造成的。

2 机器人设计与运动学分析

2.1 机器人设计

可以将多个所提EMA模块连接在一起，以产生多自由度机器人。因此，在这项研究中，通过内置磁铁将两个双轴EMA模块连接在一起形成了一个四自由度机器人。机械结构如图5所示。

图5 四自由度机器人的机械结构

装配后的机器人体积仅为15 mm×15 mm×40 mm，两个模块的总质量仅为6 g。机器人连杆长度是l1=10 mm，l2=20 mm，l3=10 mm。由于采用模块化的设计，机器人的自由度可以增加到2的倍数，即每个模块可用的关节数。然而，串联模块的最大数量受到EMA产生的最大力矩的限制。考虑到产生的最大力矩为100 mN·m，那么所提EMA最大能够保持(3个模块×3 g)垂直于1 m长的力臂。

2.2 正向运动学分析

在给定机器人关节角值的情况下，正向运动学被用来求出末端执行器的位置和方向。在图6所示坐标系上，为四自由度机器人确定了标准的Denavit-Hartenberg(D-H)参数[13]，如表1所示。

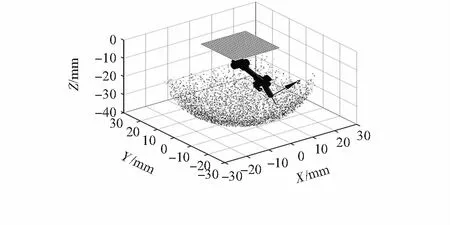
图6 四自由度机器人的工作空间

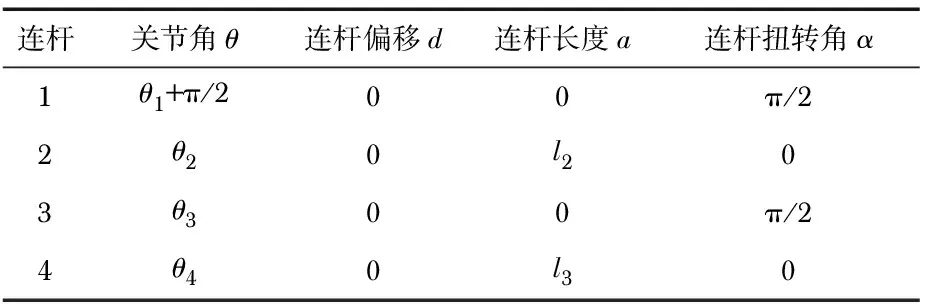
表1 四自由度机器人的D-H参数

每个关节的齐次变换矩阵可由式(6)计算得到

(6)

式中θi为第i个关节处的关节角，di为第i个关节处的连杆偏移，αi第i个关节处的连杆长度，αi第i个关节处的连杆扭转角。

(7)

由于四自由度机器人是顶置式的的机器人(即向下)，所以,机器人底座的坐标系从默认的O-XYZ变换为O0-X0Y0Z0，如图6所示。底座变换矩阵Tb可以通过在式(6)中代入θ=-π/2，d=-10，α=-π/2和a=0来获得

(8)

在关节角限制为±π/4时,四自由度机器人的工作空间如图6所示。

2.3 逆运动学分析

求解逆运动学问题在机器人应用中通常很重要，因为它用于确定实现预定义末端执行器姿势(位置和方向)所需的关节变量。这个问题通常比正运动学问题更复杂，因为它涉及到一个多变量的非线性方程的求解。在本研究中，使用代数方法解析地获得了逆运动学问题的封闭解。使用这种通用的解决方案，机器人可以在工作空间内实现任何所需的姿态。该解通过求解式(9)得到

(9)

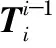
(10)

式中 (X,Y,Z)为末端执行器的位置，rij为末端执行器方向矩阵的元素。

因此，可以得到关节角的逆运动学封闭解，如下所示

θ1=arctan2(Y-l3r21,l3r31-l1-Z)

(11)

θ4=arctan2(-r21cosθ1-r31sinθ1,

-r22cosθ1-r32sinθ1)

(12)

θ2+θ3=arctan2(r23sinθ1-r33cosθ1,-r13)

(13)

(14)

θ3=(θ2+θ3)-θ2

(15)

为了验证该逆运动学解，进行了仿真试验。在此仿真中，末端执行器围绕全局Z轴旋转一个角度(φ=2π rad)，在XY平面中以固定的方向形成一个圆形轨迹。

该圆形轨迹是随机选择的，以验证使用获得的逆运动学解跟踪工作空间内任何预定义轨迹的能力。描述末端执行器在整个轨迹中方向的旋转矩阵Ro为

(16)

该预定义轨迹的半径为

(17)

根据该公式，半径R与末端执行器在Z方向上的位置直接相关。因此，该机器人末端执行器在Z方向距离为-39.6 mm的情况下，可以在XY平面上实现半径为3.97 mm的圆。实现该圆形轨迹所需的关节角如图7所示。

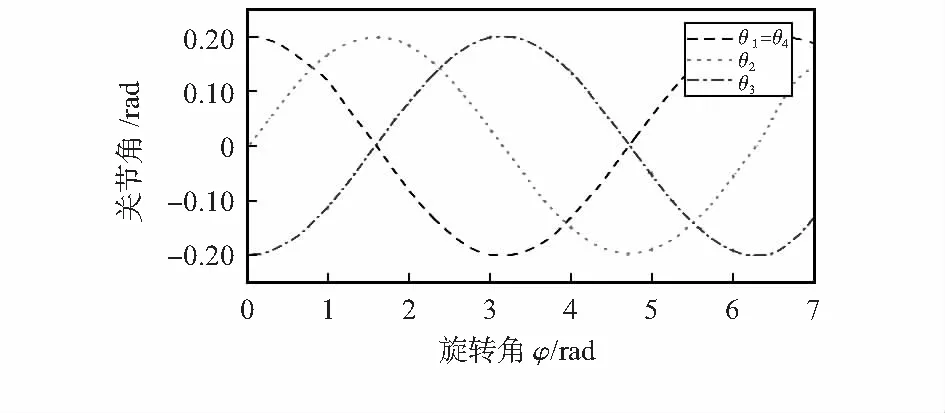
图7 圆形轨迹所需的关节角

3 实验结果

3.1 实验设置

本实验使用真实的机器人在三维空间中沿着圆形轨道运动，重复了在仿真中进行的相同测试场景。该样机由丙烯腈—丁二烯—苯乙烯(ABS)材料通过3D打印技术制成。使用Arduino Due单片机通过电机驱动器来控制机器人的方向和位置。此外，使用带有按钮和下拉电阻器的面包板来模拟不同的测试场景。实验设置如图8所示。

图8 实验设置

由于该机器人是一个微型系统，尺寸有限，而且很难在每个关节上安装内部传感器来检测末端执行器的位置。因此，在本研究中，使用非接触式传感器(1 600万像素数码相机)来检测末端执行器的位置。两个摄像机分别安装在机器人的前端和侧面，以便能够在3D空间中找到末端执行器的位置。末端执行器上标有一个蓝色的小球，通过图像处理技术更容易辨别。四自由度开环控制系统框图如图9所示。

图9 四自由度开环控制系统框图

3.2 开环跟踪测试

通过对关节施加适当的输入信号(由正弦函数生成)，如图7所示。末端执行器的位置将为沿圆形轨迹移动。采用MATLAB来实现末端执行器的目标检测和目标跟踪，具体使用了Shi J等人[15]开发的最小特征值算法来寻找特征点。目标跟踪则采用Gehrig D等人[16]提出的EKLT(Event Kanade Lucas Tomasi)特征跟踪算法，在前视和侧视摄像机获取的视频中跟踪末端执行器。末端执行器的实际轨迹如图10所示。

图10 末端执行器的实际轨迹

样机生成的轨迹比仿真生成的路径要小，主要原因是仿真分析没有考虑重力的影响。此外，样机中存在的摩擦力限制了运动，主要原因是该样机由低成本的3D打印技术制造而成，表面光洁度较差。然而，虽然仅采用简单的开环控制系统，所生成的环形轨迹在大多数情况下仍能获得良好的响应，只是在某些位置存在一定的误差。总体而言，尽管存在这些机械误差，样机的性能仍然是合理的，验证了所设计机器人的操作理念。