龟型耐压壳设计及屈曲数值分析
2022-04-12朱镇扬连雪海
李 凯,朱镇扬,连雪海
(1.江苏科技大学 机械工程学院,江苏 镇江 212000;2.中电科(宁波)海洋电子研究院有限公司,浙江 宁波 315040)
0 引言
长江是我国重要的运输河流,但目前面临繁重的生态环境修复任务,急需使用潜水器代替人工完成高危的水下工作。而耐压壳作为潜水器的关键结构,发挥着承受水压、保护内部元件的作用,占潜水器总质量的1/4~1/2。
现有耐压壳多为球形,虽然强度高,但空间利用率低,且在受载时对缺陷敏感。PAN等发现球形壳易在理论值压力的1/4~1/3处发生失稳,因此潜水器只能通过增大半径拓展空间,但又会带来水阻力增大的问题。基于海龟外壳生物特性设计的耐压壳与球形壳相比,具有以下优势:外形呈流线型,具有较小水阻力;扁平状结构使其具有更高的稳定性,有助于在湍急的江水中保持平衡;曲率相对小,空间利用率高,可使潜水器搭载更多功能模块。
为此,本文进行龟型耐压壳的设计,研究等屈曲设计下的壳体厚度变化规律,最后基于数值法进行屈曲分析。
1 耐压壳设计
海龟外壳扁平,中间宽、两端窄,截面上呈椭圆弧状。在此基础上,考虑用椭球形壳与球形壳的结合相拟合。在直角坐标系下,本耐压壳由方程(1)绕轴旋转180°而成,见图1。图中:为椭圆半长轴;为椭圆半短轴;为圆心与圆心′之间的距离;为圆的半径;′为圆心;为椭圆与圆的切点;为椭圆上点,坐标为(cos,sin);为以为半径的圆上的点,坐标为(cos,sin);为以为半径的圆上的点,坐标为(cos,sin);与互为垂线,为垂足;为∠′。
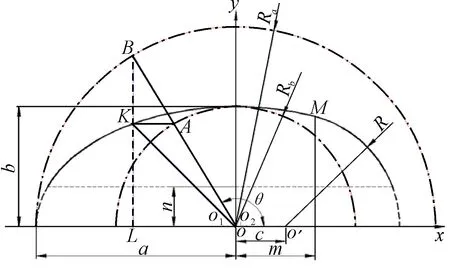
图1 耐压壳几何参数
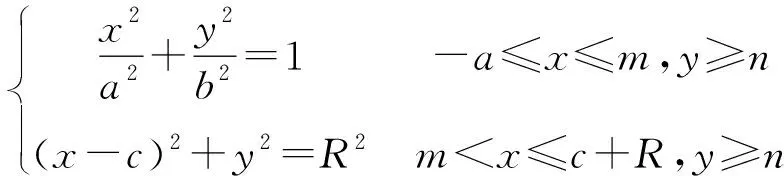
(1)
式中:为椭圆与圆方程相交的横坐标;为所截取壳体部分距原点的纵坐标。
选择耐压壳基本参数为:为200 mm,为120 mm,为50 mm,为110 mm,为80 mm,为40 mm。
耐压壳等厚设计会导致安全裕度过剩,同时浪费原材料,成本高。等屈曲变厚设计可以减少壳体材料的使用,在降低成本的同时,又保证良好的抗压和抗冲击能力。壳体由椭球壳部分与球壳部分共同组成,模型见图2。
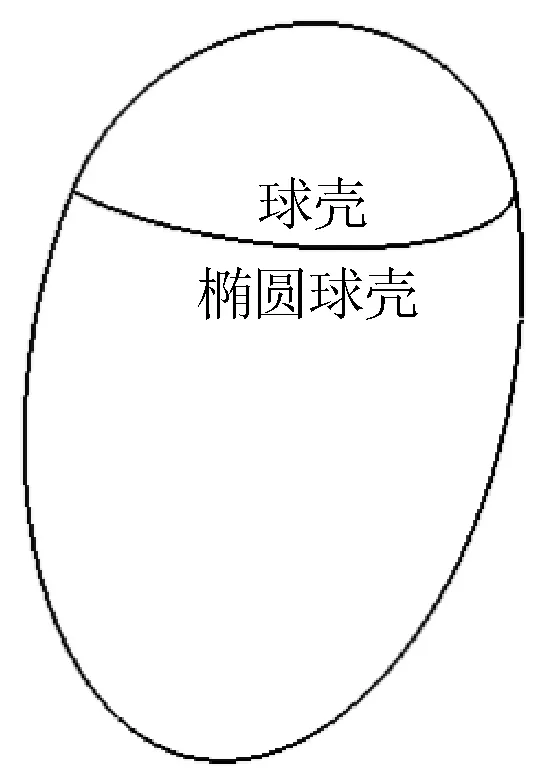
图2 耐压壳模型
对于椭球壳部分,椭球体第一曲率半径、第二曲率半径的表达式在通过椭圆参数方程:
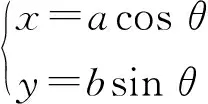
(2)
简化后,可表示为
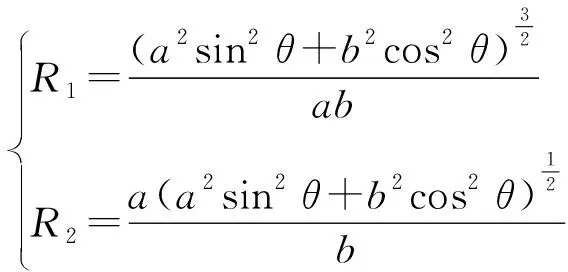
(3)
在线性范围内,根据Mushtari的屈曲理论公式,屈曲载荷可以用下式计算:
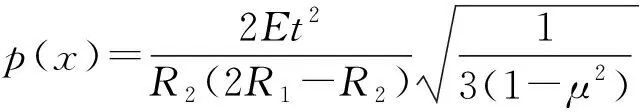
(4)
对于球壳部分,Zoelly的经典屈曲理论公式,屈曲载荷可以用下式计算:
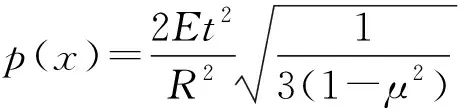
(5)
式中:为弹性模量;为泊松比;为壳厚。
现对椭球壳部分等屈曲变厚,将式(3)代入式(4),反解出,得等屈曲椭球壳厚度表达式:
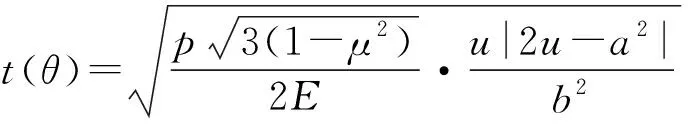
(6)
式中:=sin+cos;为壳体所受到的水压,由于壳体自身的垂直高度(-)与水深相比可以忽略不计,因此取定值。
通过求导,发现以下厚度变化规律:
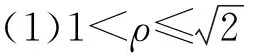
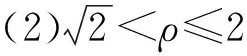
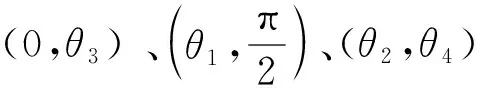
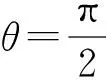
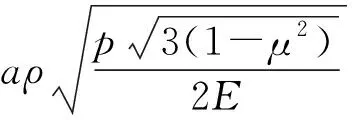
(7)
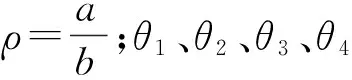
现对球壳部分等屈曲变厚,对式(5)反解出,得等屈曲椭球壳厚度表达式:
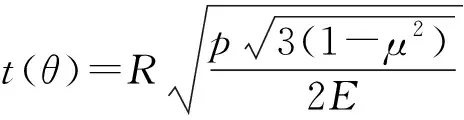
(8)
在水压、材料和半径确定时,()为常数。
2 屈曲数值分析
2.1 数值模型
在设计中,考虑到长江流域水深,要求耐压壳能够承受50 m深的水压,相应水压=0.49 MPa,并取安全系数=1.5。选择树脂材料,其性能参数为:=2 400 MPa,屈服强度[]=33.22 MPa,泊松比=0.41,=3.6 mm。采用前处理软件ANSA对网格进行划分。应力分析模型多采用四边形壳单元,共获得13 791个网格,见图3。
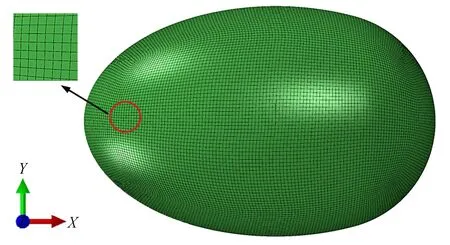
图3 网格划分
考虑到安全系数,对壳体外表面施加均布载荷=0.735 MPa。约束定义:限制底部边界所有节点的平移和旋转的自由度,即===0且===0。
2.2 数值计算结果分析
利用ABAQUS软件对耐压壳模型进行线性屈曲求解,得到前2阶屈曲模态。前2阶模态云图见图4。在线性屈曲分析下,耐压壳模型临界屈曲载荷为0.79 MPa,高于水压0.735 MPa,材料符合要求。通过云图发现,屈曲容易发生在壳体的上下及中间部分。由于材料制造过程存在初始缺陷,真实部件可能在低于理论值的载荷下发生屈曲,因此线性屈曲分析下的临界载荷相对偏大。
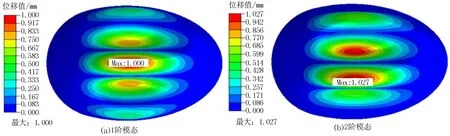
图4 前2阶模态云图
采用ABAQUS软件的Riks算法进行非线性屈曲分析,其应变云图见图5。由图5可知:在非线性屈曲分析下,其临界屈曲载荷为0.76 MPa,高于水压0.735 MPa,材料符合要求。其他结论与线性屈曲分析相同。
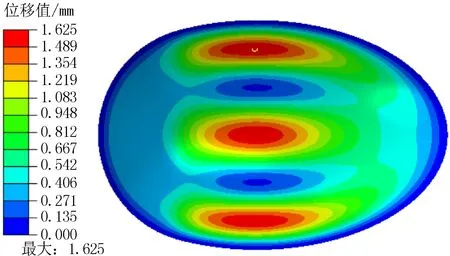
图5 应变云图(弧长=1.41)
3 结论
(1)由壳体厚度表达式可知,无论椭圆率在哪个范围,椭球形壳体部分的厚度在=π/2处取最大值,球形壳体部分的厚度为常数。
(2)基于数值法的屈曲分析结果表明,龟型耐压壳的上下及中间部分为壳体的薄弱环节,最容易发生破坏。
