新高考背景下复习策略分析——以圆锥曲线问题为例

许智超

(扬州大学数学科学学院,225002)

2019年,教育部考试中心研制并发布《中国高考评价体系》，提出 “一核”、“四层”、“四翼”等要求，结合2020年最新修订的《普通高中数学课程标准》的相关要求，对2020年新高考的设计与命题工作具有十分重要的指导意义[1][2].

2020年山东试点启用新高考I卷.2021年江苏、湖北、河北、广东、湖南、福建六省加入启用新高考I卷.对考生而言, 试卷的不同导致复习备考上的侧重点也将会有所不同;而对教师来说在新高考背景下，如何改进复习教学也是一场全新的挑战.

本文选择2021年新高考I卷、2020年新高考I卷中的圆锥曲线试题，按照思想方法进行分类,分析新高考背景下圆锥曲线命题的变与不变，并据此给出新高考背景下圆锥曲线的复习策略与教学分析.

一、基于思想方法分类的真题分析

1.圆锥曲线基本概念与公式的直接应用

例1(新高考2020年I卷)已知曲线C:mx2+ny2=1.

(A)若m>n>0,则C是椭圆,其焦点在y轴上

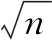
(D)若m=0,n>0,则C是两条直线

2.圆锥曲线问题中的函数与方程思想

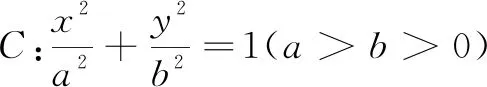
(1)求C的方程;

(2)点MN在C上,且AM⊥AN，AD⊥MN,D为垂足,证明:存在定点Q,使得|DQ|为定值．

①

分析此题第(2)问是2020年的压轴题.从题型来看是考生熟悉的定点定值问题，所以离不开直线与圆锥曲线的基本模式: 联立直线与圆锥曲线方程——利用韦达定理建立交点坐标与参数间数量关系——化简参变量函数——建立某个主变量(如面积)函数或点斜式直线方程等[3].通过对直线MN的方程的分析可以得出其过定点P, 进一步发现所要寻找的点Q在直线AP上，从而得出答案.对于考生来说，除了以上所说的寻找定点P，解决这道题目最大的障碍就是其复杂的运算过程考虑到此题安排在最后一题，大部分考生会出现时间不够的情况，无疑增加了解题的难度.

3.与其他知识内容的综合运用

例3(新高考2021年I卷)如图2，已知O为坐标原点，抛物线C:y2=2px(p>0)的焦点为F,P为C上一点，PF与x轴垂直,Q为x轴上一点,且PQ⊥OP, 若|FQ|=6，则C的准线方程为______．

二、基于真题分析的复习备考建议

1.加强圆锥曲线概念与公式的掌握

熟悉并掌握圆锥曲线的基本概念与基本公式是最终解答问题的根本.在教学过程中，注重知识的生成过程，帮助学生理解掌握基本概念与基本公式;而在复习阶段，有意识地引导学生收集并记住一些常见的二级结论与二级公式，可以节约时间与有效提高正确率.如21年的解答题第(2)问，用斜率和横坐标表达两点之间距离.

2.熟练利用函数与方程思想

尽管新高考试题的问题和研究对象都可能发生变化，但解决问题的基本方法是类似的，在变中寻找不变，尤其是解答题都要经历一个设参、联立、利用韦达定理消参的过程.其实，在解题教学课上初次出现时，就应要求学生对此有一个基本认识.而在备考复习阶段，则要专门训练达到熟练的地步

3.在求解过程中注意与其他内容产生知识联结

圆锥曲线主要考查的是圆锥曲线的相关知识，但不仅仅只考查圆锥曲线.2021年的第5题涉及了基本不等式，第14题需要利用相似三角形来求解长度，2020年解答题所要求的定点与定长其实就是圆心与半径.一些非圆锥曲线知识经常出现在解决圆锥曲线的问题中，尤其是几何图形的相关内容，比如三角形、特殊的四边形、圆的相关性质往往可以成为解题的突破口