基于改进K-means算法的电力短期负荷预测方法研究

荀 超，陈伯建，吴翔宇，项康利，林可尧，肖 芬，易 杨

(1.国网福建省电力有限公司，福建 福州，350000；2.国网福建省电力有限公司电力科学研究院，福建 福州，350000；3.国网福建省电力有限公司经济技术研究院，福建 福州，350000；4.福州大学电气工程与自动化学院，福建 福州 350108)

随着电网智能化程度和信息化程度的不断提高，由电网维修和运行产生的数据不断增加，对大数据处理和存储提出了更高的要求，增大了管理大数据的难度，导致在信息传输、系统可靠性、信息存储和集成等方面增加了智能电网面临的挑战[1-2]。电网建设、电力营销和电力设备等产生的数据是智能电网中主要存在的电力数据，通过对这些电力数据进行分析，可以对电力短期负荷进行预测，从而保障智能电网的运行性能[3-4]。当前电力短期负荷预测方法存在预测效率和精准度不高的问题，需要对预测方法进行深入的分析和研究[5]。文献[6]提出基于集合经验模态分解(ensemble empirical mode decomposition，EEMD)和神经网络的电力短期负荷预测方法，通过EEMD样本熵分解原始的电力负荷大数据，融合各子序列的预测结果，实现电力负荷大数据的短期预测；文献[7]提出基于径向基函数神经网络(radical basis function，RBF)的电力短期负荷预测方法，该方法利用主成分分析法消除冗余信息，提取电力负荷大数据的特征向量，在RBF网络中结合历史负荷数据和提取的特征向量建立负荷大数据预测模型，实现电力负荷大数据的预测；文献[8]提出基于改进随机森林的电力短期负荷预测方法，采用遗传算法优化随机森林决策树，利用优化后的随机森林决策树实现电力负荷大数据的预测；文献[9]提出基于深度学习的多特征短期电力负荷预测，对比了多种算法下短期电力负荷预测结果的情况，选择最佳算法进行负荷预测。但以上方法均忽略了对其进行聚类处理，导致预测耗时较长、短期负荷预测精度需进一步提高。

为解决上述现有方法中存在的问题，进一步提高电力短期负荷预测的效率和精度，本文提出一种基于改进K-means算法的电力短期负荷预测方法。基于改进K-means算法的数据分类，采用循环神经网络(recurrent neural networks，RNN)模型，在RNN循环神经网络模型中输入最优权值，实现大数据环境下的电力短期负荷预测，可提高预测的效率和短期负荷预测精度。

1 基于改进K-means算法的数据分析

K-means算法核心思想：将n个数据对象划分为K个类，并且使每类中的所有数据对象到该类的聚类中心点的平方和最小，但其聚类时间比较长，为实现对数据的快速聚类，保留K-means算法的效率同时将K-means的应用范围扩大到离散数据，其K-means改进算法的计算过程如下。

1)从整个样本X中，令I=1，在X中随机挑选K个数据对象作为初始聚类中心mj(I)，其中，j=1,2,…,K。

2)设d(i,j)为K个聚类中心mj(I)与电力负荷大数据样本X中每个对象xi之间的距离，即

d(i,j)=

(1)

利用式(1)寻找d(i,j)的所有(i,j)取值对应的欧式距离中最小的欧式距离d，在聚类中心mj(I)相同的簇Sj中存储对象xi[10]。

3)设mj(I+1)为新聚类中心点，即

(2)

式中Nj为数据对象在第j个类中的数目。

4)设置判断准则，判断是否满足准则，如果满足则进行下一步，如果不满足则转到步骤2中。

5)输出电力负荷大数据的聚类结果。通常情况下利用判断准则对是否终止循环进行确定，即①聚类中心点相同，当第I次迭代和第I-1次迭代获得的划分结果相同时，认为划分合理，结束迭代；②离散度准则函数，当第I次迭代对应的聚类离散度与第I-1次迭代对应的聚类离散度之间的差值小于计算得到的收敛极限值时，认为划分合理，停止迭代[11]。聚类离散度函数为

(3)

设置收敛极限值ξ，当|Jc(I)-Jc(I-1)|<ξ时，停止迭代。

对其聚类方法进行改进，通过混沌理论优化自由搜索算法进行计算，具体过程如下。

①通过随机值策略获得初始化种群，即

x0ji=Xmini+(Xmaxi-Xmini)rji(0,1)

(4)

式中i为第i个变量；j为第j只个体，j=1,2,…,m，其中m为个体数目；n为搜索空间在Elman网络中对应的维数，即变量在目标函数中的总数；Xmini、Xmaxi分别为第i维变量在Elman网络中存在的最小值和最大值；rji(0,1)为随机数。

②设Pj为信息素，其计算式为

(5)

Sj=Smin+(Smax-Smin)rj(0,1)

(6)

式(5)～(6)中Smin为灵敏度对应的最小值，存在Smin=Pmin；Smax为灵敏度对应的最大值，存在Smax=Pmax。利用计算得到的初始信息素，获得初始搜索结果[12]。

③设xOj为灵敏度，其计算式为

(7)

在新一轮中，根据式(7)计算的结果，在Elman网络中选择搜索的起始点。

④经过初始化处理后，个体在Elman网络中随机产生T个坐标，得到最佳适应度坐标，即

(8)

式中t为当前搜索过程中的搜索小步；Rji为搜索空间中第j个体在Elman网络中的空间邻域搜索范围，其取值范围为Rji∈[Rmin,Rmax]。

⑤在适应度优劣的基础上确定普通粒子和精英粒子[13]。基于改进K-means算法的电力短期负荷预测方法通过Tent映射确定精英粒子，即

(9)

通过式(9)获得K个点对应的混沌点列，原精英粒子在Elman网络中的位置对应适应度值最好的点。

⑥释放信息素，并存储最佳个体。

⑦设置终止条件，若符合设置的终止条件，则输出搜索结果。

2 电力短期负荷预测方法

图1 RNN循环神经网络结构Figure 1 Structure diagram of RNN recurrent neural network

设w1i,j、w2i,j、w3i,j分别为节点从输出层到隐层、从隐层到输入层、从输入层到输出层对应的权值；M为输入Elman网络的节点数量，本文中输入Elman网络的节点数为300；N为输出Elman网络的节点数量，输出Elman网络的节点数为100；L为隐层中存在的节点数量，本文取该节点数量为400。

(10)

(11)

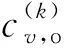
(12)

(13)

根据输出向量构建训练指标函数，即

(14)

当紫薯粉的添加量为40%、黄油添加量为50%、柠檬酸添加量为0.4%的条件下，白糖添加量分别为10%、15%、20%、25%、30%，研究白糖添加量对紫薯酥性饼干品质影响，感官评分结果（见图3）。白糖添加量在20%的感官评分最高，紫薯饼干甜度的来源一方面是添加的白糖甜度，另一方面是紫薯粉本身的甜度，所以紫薯酥性饼干中白糖的添加量要低于普通饼干中白糖的添加量。当白糖的添加量小于20%时，饼干甜味较淡，上色效果不均匀，且口感较硬，当白糖的添加量大于20%时，饼干过甜，边缘易出现焦糊现象。因此选择白糖添加量为20%。

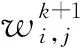
(15)

(16)

(17)

(18)

(19)

3 电力短期负荷预测过程

基于改进K-means算法的电力短期负荷预测方法的预测流程如图2所示。

图2 电力短期负荷预测流程Figure 2 Flow chart of power load short-term forecasting

电力短期负荷的预测过程如下。

1)利用K-means聚类算法对电力负荷大数据进行聚类处理，获得训练样本，构建RNN网络拓扑结构。

2)对种群进行初始化处理。

3)通过个体解码计算对应的初始权值，在训练样本数据的基础上对RNN神经网络进行训练，将期望和预测输出误差作为个体适应度值ftj，即

(20)

式中E为期望输出误差；K为常数。

4)搜索、计算个体对应的灵敏度Sj和初始信息素Pj，通过对比结果对连接权值进行优化。

5)设置终止条件，对输出的负荷预测值与电力负荷的实际值进行判断比较。若满足预先设定的最小误差，则停止迭代。判断是否满足条件，若满足则进行下一步，若不满足则返回步骤3中。RNN神经网络中存在的初始权值通过混沌自由搜索算法进行优化，获得最佳权值[15]。

6)负荷预测。在RNN神经网络中输入最权值作为优化参数组合，获取最优初始权值，实现电力短期负荷的预测。

4 实验与结果

为了验证基于改进K-means算法的电力短期负荷预测方法的整体有效性，在Matlab平台上进行测试。输入Elman网络的节点数量为300，输出Elman网络的节点数量为100，隐层中存在的节点数量为400。负荷预测样本数量为1 000个。对基于EEMD-样本熵和Elman神经网络的文献[6]方法、基于大数据简约及PCA改进RBF网络的文献[7]方法与本文方法进行对比测试，对比不同方法预测电力负荷大数据消耗的时间，测试结果如图3所示。

由图3中的数据可知，在多次迭代中本文方法预测电力负荷大数据消耗的时间均少于文献[6]和文献[7]方法消耗的时间。因本文方法采用改进后的K-means算法对电力负荷大数据进行了聚类处理，获得了大量训练数据，减少了预测消耗的时间，提高了预测效率。

图3 不同方法的时间消耗Figure 3 Time consumption of different methods

为进一步验证方法的整体有效性，采用上述方法进行电力负荷大数据预测测试，分别对正常工作日负荷(周一到周五)、休息日负荷(周六、周日)、节假日负荷这些不同类型日负荷的预测结果，并与另外2种方法比较，进一步验证本文方法在提高短期负荷预测的精度方面的优势。对比结果如图4～6所示。

图4 工作日负荷预测结果Figure 4 Working day load forecast results

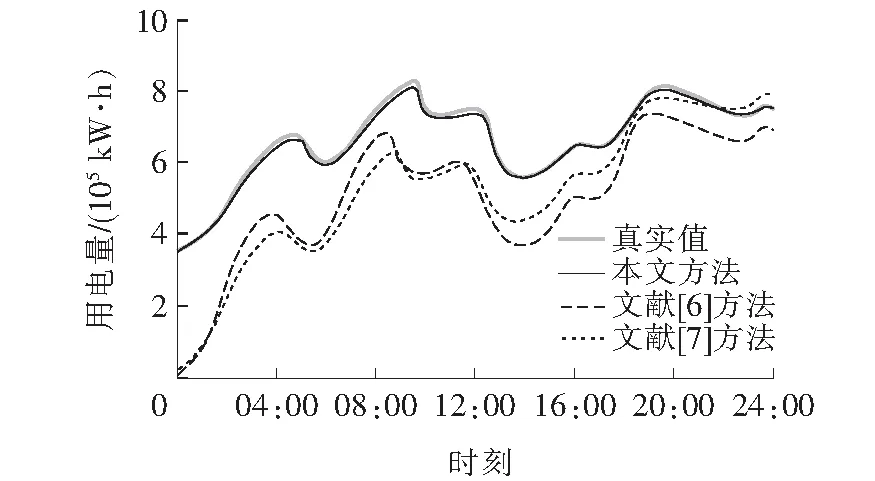
图5 休息日(周六、周日)负荷预测结果Figure 5 Rest days (Saturday and Sunday) load forecast results

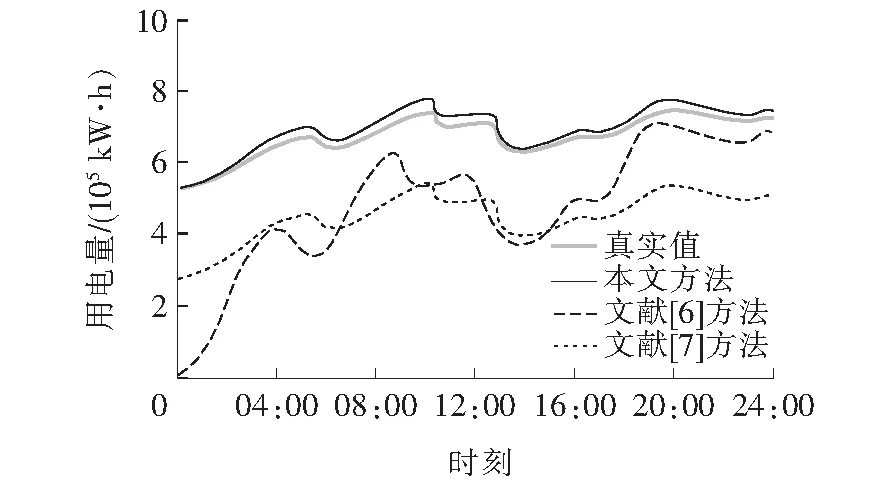
图6 节假日负荷预测结果Figure 6 Holiday load forecast results

分析图4～6中的负荷预测对比曲线可知，采用本文方法获得的预测曲线与真实值曲线相差不大，精度始终接近96%。文献[6]、[7]的精度最高为92%，此方法获得的预测曲线与真实值曲线之间的差距较大。因为本文方法利用K-means聚类后获得的训练样本对RNN神经网络进行训练，通过混沌自由搜索算法获得最佳权值，实现电力负荷大数据的精准预测，验证了本文方法的预测精准度。

为进一步验证方法的聚类处理后的效果，在1 000个数据样本中，选取100个样本数据，数据样本通过五角星形状、三角形状以及圆形表示。分别采用上述几种方法进行测试，对比不同方法预测电力短期负荷大数据聚类结果，如图7所示。

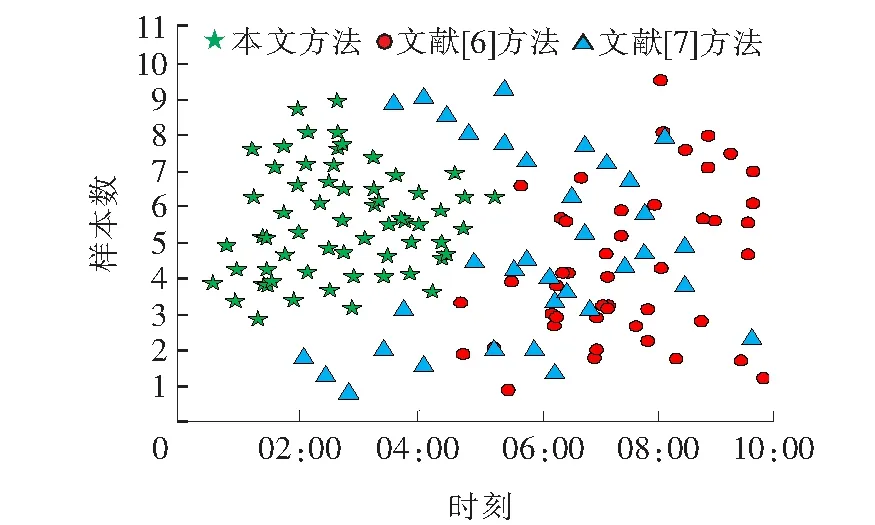
图7 不同方法的聚类结果Figure 7 Clustering results of different methods

分析图7中的数据可知，采用本文方法获得的数据紧密聚集，聚类性较好，采用文献[6]、[7]方法获得的数据比较分散，聚类性较差。因为本文采用混沌理论优化自由搜索算法进行聚类优化，通过改进后的K-means算法对电力负荷大数据进行了聚类分析。

5 结语

电力负荷大数据的复杂性随着电力系统的发展不断增加，目前电力负荷大数据的预测方法已经难以满足电力系统的需求，使电力负荷大数据预测成为目前亟需解决的问题。当前电力短期负荷预测方法存在预测效率低和预测精准度低的问题，现提出一种基于改进K-means算法的电力短期负荷预测方法，利用改进后的K-means算法对电力负荷大数据进行分类处理，通过RNN神经网络高效、精准的实现电力负荷大数据的预测，可以满足现有电力系统无法解决负荷大数据复杂性的需求，提高短期负荷预测的精度，为电力系统的发展奠定了基础。