WSN中基于强化学习的能效优化任务处理机制

张明杰 朱江

（重庆邮电大学通信与信息工程学院，移动通信教育部工程研究中心，移动通信技术重庆市重点实验室，重庆 400065）

1 引言

物联网（internet of things，IoT）时代的来临促进了无线传感器网络（wireless sensor network，WSN）的部署，由于WSN 现有以及潜在的广泛应用，使其被确定为当今最重要的技术之一［1］。但因为计算能力和电池容量的限制，无线传感器通常无法有效处理复杂的计算任务，因此，如何提升计算能力和能量效率是WSN 研究的热点领域。国内外对于无线传感器能量效率的研究主要分为资源的合理调度［2-4］以及运用能量收集技术（energy harvesting，EH）对无线传感器进行充能［5-8］。

为了满足更多场景下任务处理需求，将边缘计算与WSN 相结合。移动边缘计算（mobile edge computing，MEC）能够在网络边缘为用户提供计算卸载和数据缓存，为用户提供更加高效的存储和传输。采用基于边缘计算的任务卸载技术可提高任务处理效率［9］。然而，在边缘计算中，将整个计算任务卸载到边缘计算服务器的方式能效不高，因此某些任务应由本地计算执行［10］。文献［11］定义了一种卸载优先级函数，将部分任务卸载到边缘进行计算。在满足时间延迟的前提下，提出有效的卸载决策以最小化能源成本是一个关键问题［12-15］。通过对缓存器内任务的部署，可以有效提升任务处理过程中的能量利用率，降低网络能耗［16-17］。

将WSN 与边缘计算结合后，数据能够得到处理，但二者的自组织能力以及对于环境的适应性有限，为解决相应问题，国内外学者采用人工智能［18］方法对传感器不同的任务卸载场景进行智能调度，降低了系统能耗。文献［19］提出了一种基于强化学习的隐私感知卸载方案，应用Dyna算法框架提供模拟卸载以加快学习过程，从而提高计算性能。文献［20］针对具有EH 的IoT 设备提出了一种基于强化学习的卸载方案。文献［21］采用二进制卸载策略的无线MEC 网络，提出了基于深度强化学习的DROO 在线卸载算法框架，降低了计算复杂度。文献［22］提出了一种自适应睡眠/唤醒调度方法，在不牺牲数据包传递效率的情况下，节省每个节点的能量。然而，上述工作主要集中在提升传输速率和降低计算复杂度，较少有学者考虑物理层以及数据链路层参数对系统能量消耗的影响。但相关参数对系统能效的提高有着重要的意义。

为了提高无线传感器设备系统的任务处理能效，本文研究了基于能效的任务处理机制，主要工作如下。

（1）建立了基于马尔可夫决策过程的任务处理机制。物理层以及数据链路层的最佳控制角度考虑任务本地计算和边缘计算能量的联合优化，通过智能优化代理得到任务到达缓存区后取出的本地计算任务量和卸载任务量，保证任务得到有效处理的同时得到近似最优的系统能效。

（2）利用强化学习代理通过贪婪策略进行动作探索和利用从而获得最佳的卸载策略。针对在线学习收敛速度慢的问题，A3C 算法采用异步训练框架加快学习收敛速度。

2 系统模型

图1是多个无线传感器网络的节点进行任务处理的模型，每个无线传感器buffer 的处理情况都和节点2相同。每个无线传感节点采集到的数据被封装成待处理的任务，存储在内部的缓存器中。每隔相同的时间段（时隙），节点从缓存器内取出一定数量的任务进行处理：即一部分任务卸载到边缘服务器进行处理，一部分由传感器消耗自身资源进行本地处理。

当有任务卸载到边缘服务器进行处理，在每个时隙内，各个无线传感节点会以CDMA 的方式将任务数据发送到边缘服务器端。因此，系统采用的是以时隙为时间单位的时分多址与CDMA 混合的多址方式。一个节点经历的无线信道干扰取决于其他节点采用的传输功率（详见4.3节）。每个节点根据其缓存区内任务数量和测得的信道状态独立地学习其任务处理策略。

单个无线传感器节点与边缘服务器的任务处理框图如图2 所示。设缓存器长度为L，λ为一帧内任务到达缓存器的平均到达率，λ服从泊松分布。某一帧开始时节点i缓存器内任务量为为从缓存区内取出的任务数量，取出的任务数量分成本地计算以及边缘计算两部分，则有

δ={ACK，NACK}为边缘服务器反馈的接受确认信息，成功接收为ACK，失败则返回NACK，I{·}为指示函数，括号内为真，函数值返回1，否则返回0。

在传输之前，可以通过发送导频信息获得边缘计算服务器端反馈的信道状态信息（channel state information，CSI）。智能控制代理观察缓存区内任务量以及前一次传输的信道增益，在此基础上，决定从缓存区取出多少任务进行本地计算和卸载以及获得相应的最佳传输功率和调制级别，使任务得到有效处理的同时近似最大化系统能效。若某信道的任务数据被成功接收，接收机将反馈确认消息ACK，否则反馈失败消息NACK。没有被成功发送的任务数据将被重发。

3 能耗分析

任务处理过程中，所消耗的能量主要由三部分构成，分别为本地计算能量、卸载能量以及从边缘服务器下载任务处理结果所耗能量。由于计算结果下载能量相较于本地计算能量以及计算卸载能量可以忽略不计，本文暂不考虑。

3.1 本地计算能耗

本地计算能量消耗取决于本地计算任务量以及无线传感器节点的计算能力，假设CPU 频率在每个节点处为固定值，Ci为节点i计算1比特数据需要的CPU 周期数，Pi为该节点进行本地计算每个CPU周期的能量消耗，则节点i一帧内本地计算总能耗表达式为

3.2 卸载所耗的能量

在本地计算时间不能满足时延约束的情况下，将多余任务卸载到边缘服务器进行计算。任务卸载所采取的传输功率取决于强化学习代理所做的决策。卸载所消耗的能量如下式所示：

4 基于MDP的任务处理机制

将基于系统能效的任务传输调度机制建模为马尔科夫决策过程，其状态、行为、状态转移概率以及回报函数被定义为(S，A，P，R)四元组。

4.1 状态集S

包含所有可能状态的状态空间，在本文中，状态空间定义为关于缓存区任务量、信道增益的聚合状态，其中为节点i缓冲区内的任务量，γi为卸载任务时节点i信道的信道增益。

4.2 行为集A

包含所有可能行为的行为空间，在本文中，行为空间定义为智能控制代理根据状态空间选取的调制等级和发射功率以及从缓存区取出的任务量，表示为状态空间由信道增益以及缓存器内任务数量构成，每转换到一个新的状态会得到信道增益以及缓存器当前任务数量参数，根据两个参数，行为空间根据奖励函数选择出最优的从缓存区取出的任务数量、调制等级以及发射功率，当缓存器内任务数量多时，需要使用高的调制等级增加传输吞吐量以满足任务处理需求。为节点i从缓存器内取出的任务量，mi为节点i根据状态选择的调制等级（BPSK-8PSK）为节点i相应调制 等级的发射功率。

4.3 状态转移概率P

使用有限状态马尔可夫信道对无线信道动态进行建模［23-24］，将等效信道增益划分为有限数K个区间，0=Γ0＜Γ1… ＜ΓK，信道增益在ΓK-1到ΓK间则称为状态k，在服从瑞利衰落的信道中，γ呈指数分布，概率密度函数为p(γ)=1/γ0exp(-γ/γ0)，其中γ0是平均信道增益。

稳态概率为

状态转移概率为

其中N(Γ)=是电平交叉函数，fd是最大多普勒频率。πk为状态sk下选择行为ak的概率。

任务成功分组传输概率为

令K表示成功发送所需的重传次数，设每次传输都是独立的，则K的概率质量函数为

得到了成功分组传输概率以及信道状态转移概率，相应的节点状态转移以及转移概率为

传输成功：

传输失败：

4.4 奖励函数R

在WSN 的应用中，能耗、吞吐量以及时延都是非常关键的因素，在最小化能源消耗的同时，如果任务处理数量太少或延时太大都是不可接受的。因此，采用总消耗的能量成功处理的任务量作为目标函数。从缓存区内取出的任务分为本地计算以及卸载到边缘两部分分别进行处理。系统的目标函数为每总消耗能量的成功任务处理数量，则一帧内效用函数表达式为

式（11）中PΓ(Γi，m)为任务成功分组传输概率，效用函数的单位为任务处理数量每焦耳。假设卸载一个任务所包含数据的信息比特为Lb与添加错误解码代码后的任务数据信息比特为L。传输速率为Rbbit/s。传输消耗能量为

由于任务到达速率的不同，不可预知下一状态即将到达多少任务量，如果任务量过多，而采用的卸载策略卸载任务量小，则根据当前缓存区内所剩余的任务数量对当前奖励函数进行惩罚，迫使当前状态时，选择卸载任务量更大的行为。为了最小化缓存区溢出的可能性，将缓存处理成本合并到奖励函数中，提高服务质量（Quality of Service，QoS）。奖励函数表示为

奖励函数前一项为每单位总能量消耗后任务成功处理量。后一项是缓存区处理成本，权重ε在防止缓冲溢出的同时，使得缓存处理成本降低。奖励函数由贝尔曼方程驱动，通过循环迭代的方式获得计算回报值R(s，a)。

由于需要的是最大化每个用户总消耗能量的长期平均任务处理量，因此关注于每个阶段的平均奖励，表示为：

式（13）中π(sk)为sk状态下采取的策略，E(·)为取均值。

5 求近似最优解

在已知状态转移概率以及信道状态完美的情况下，对于任何马尔科夫决策过程，存在一个最优策略π*，优于或至少不差于所有其他策略，根据已知的缓存区任务数量通过策略迭代选择出最佳即使得价值函数最大的调制等级以及发射功率，带入效用函数中可以得到相应状态下的最优能效值，不同状态下的得到的能效值不同，对所有状态下的最优能效值求平均，得到平均最优能效。本文仿真之所以能得到最优值，其实是假设预知某个状态时，选择相应行为能获得最优能效，然而在大部分场景中，这个假设难以成立，即难以获得状态转移概率，以及完美的信道状态，故采用强化学习算法得到接近最优的平均能效值。

本节中运用Asynchronous Advantage Actor-critic算法解决MDP 每个阶段的平均回报值。相较于AC算法、Dyna 算法以及DROO 算法，A3C 算法利用同时在多个线程里面分别和环境进行交互学习的方式，算法框架如图3所示，每个线程即代表根据不同的信道增益以及缓存区任务数量，选择不同的从缓存区取出任务数量、调制等级以及发射功率后，与环境交互得到该线程的回报值。每个线程都学习出自己的成果，最后把所有子网络的学习成果汇总起来，整理保存在一个公共的全局网络中，并且，子网络会定期从公共网络中学习成果回来指导自己和环境之后的学习交互。回避了相关性过强的问题的同时还做到了异步并发的学习效果。由于A3C 算法中各个子线程相互独立，对单个子线程进行分析可推广至全局。

算法的本质为更新相对状态值函数h(s)以及平均奖励值ρ，建立本文贝尔曼驱动方程为

状态值更新与奖励值更新可表示为

通过贝尔曼驱动方程，可以消除对状态转移概率的需求，相对状态值函数具体更新过程为

平均奖励值更新与上式相似

式（16）、（17）中αk与βk决定了状态值函数和平均回报值的当前和未来预估的权重。式R(sk，π(sk)) +hk+1(sk+1)-hk(sk)-ρk称为TD error（time slot error），其指导着学习过程，确定状态值函数和平均奖励的学习率。

算法初始化时随机进入一个状态sk，则选择行为的概率服从均匀分布，为了选出奖励函数更大的行为，算法设定了偏好值，其更新公式为

式中ηk决定了偏好值的学习率。算法中初始偏好值p(sk，ak)=0，∀s∈S，∀a∈A，算法最初会统一选择每个动作的概率，随着迭代的进行，通过增加选择该特定动作的偏好值来确定导致相对状态值函数增加的行为的优先级。相反情况下，如果TD error 为负时，通过降低其偏好值而受到惩罚，导致相对状态值函数减小。

完整的A3C 算法如表1 所示，由于A3C 是异步多线程的，在此给出任意一个线程的算法流程。首先初始化全局网络参数，然后将全局网络同步到所有子线程Actor 与Critic 网络，子线程经过参数学习迭代后，将最优的学习效果同步到全局网络，同时，更新所有子线程的学习参数为当前最优全局参数。

表1 A3C算法Tab.1 A3C algorithm

Actor根据概率选择决策，条件概率越大的状态行为被选择到的可能性就越大。算法最初开始时每个动作被选中的概率均等，Actor在初始阶段可能选择任何可用的动作，这也称作探索阶段，与所有的强化学习算法相似，A3C 算法在学习过程也需要经过平衡探索和利用的步骤。利用阶段的意义在于搜索平均奖励最大化的决策，而探索步骤的意义在于尝试所有可能的最佳决策，避免陷入局部最优解。

6 仿真结果与分析

6.1 参数设置

本次实验使用的电脑主频为3 GHz，内存为8 GB，处理器 为Intel（R）CORE（TM）i5-8500（四核），故仿真设置子线程数为4，电脑的操作系统为Windows 10，使用的仿真平台为Matlab R2019a 以及Python 3.7.9 版本，神经网络模型为使用Python 中的torch 库搭建的网络模型，模型中参数如表2 所示。本次实验将本文所提算法与Dyna 算法、DROO算法、AC 算法进行对比。在对比算法中，系统参数与本文算法采用相同设置，采用自适应调制方式以及固定发射功率pt=0.8 Watt。

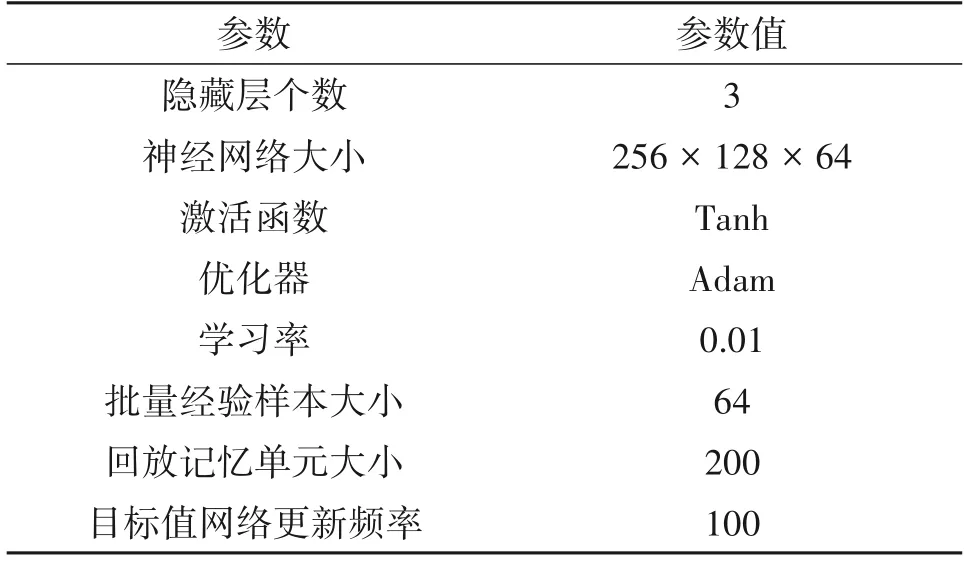
表2 神经网络参数设置Tab.2 Neural network parameter setting

本节中使用表3中所设的参数来构建仿真，仿真过程中状态集为行为集为

表3 仿真参数Tab.3 Simulation parameters

A3C算法初始化参数值αk=0.05，βk=0.005，ηk=0.01，ε=0.6，计算1 比特数据需要的CPU 周期数Ci∈[500，1500] cycle/bit，计算每个CPU 周期的能量消耗Pi∈(0，20 × 10-11) J/cycle，二者均服从均匀分布，节点计算能力Fi∈{0.1，0.2，…，1}GHz。将最佳解决方案与A3C 算法学习的策略作比较。一个任务所包含数据的信息比特为Lb=80 bit，添加错误解码代码后的任务数据信息比特为L=100 bit。将强化学习策略与最佳策略进行比较，证实了学习策略接近最优策略。将学习策略与简单策略也进行了简单比较，可以看出强化学习算法显著提高了平均任务处理量能效。将本文任务处理机制与其他文献中的任务处理机制相比较，本文提出的任务处理机制得到的平均能效明显更高。

6.2 实验结果分析

图4表示了多节点情况下A3C算法在平均任务到达速率λ=2.0 时学习到的每消耗1 毫焦耳能量平均处理的任务数，简称为节点学习值，A3C 算法能跟踪控制概率的变化，从而获得接近最优策略的能力。

在图4 中可以看出，学习到的毫每焦耳平均任务处理数非常接近最佳每毫焦耳平均卸载任务数。评估了多节点方案中独立A3C 算法的性能，用3 个节点与一个边缘服务器通信来模拟多节点系统，节点1 是最近节点，节点3 是最远节点，在此方案中，靠近边缘服务器的节点将具有更高的任务处理能效，因为它实现相同的任务处理量所需要的能量较少。

图5 表示了在不同的任务到达速率λ的情况下，A3C 学习策略与简单策略分别所实现每消耗1毫焦耳能量平均卸载的任务数。运用简单策略所得到的平均能效值称之为简单值。在简单策略中，代理选择最高可能的调制方式同时选择出给定调制方式的情况下达到预定义信号干扰比（SIR）的发射功率。应用简单策略情况下，当缓冲器中只有1 个任务时，发射机选择二进制相移键控（BPSK）进行发送，当队列中分别有2 个任务和多于3 个任务时，发射机选择正交相移键控（QPSK）和8PSK 进行发送。对于每个调制，发射机选择发射功率以实现固定的预定义SIR。对于BPSK 到8PSK，分别使用（6，10，15）dB 作为预定义的链路信噪比。由于服务器端接收任务数据的概率并非100%，传感器端未收到服务器端返回的ACK 信令，则需要重新发送任务数据，如果任务成功接收概率过低，重发次数过多，消耗能量越大，故需要满足特定任务成功接收概率，而预定义的SIR 的任务分组成功正确接收概率可以达到80%以上。

从图5 中可以看出，在任务到达速率低时（λ≤1），两种策略的所达到的平均任务处理能效差距不大，但随着任务到达率提升，A3C 算法相较于简单策略所提升的平均能效显而易见。

图6 表示了在不同任务到达率情况下，采用A3C 学习策略、Dyna 算法框架、DROO 算法框架以及简单策略所达到的平均能效值。

从图6 中可以看出，在相同的平均任务到达速率情况下，A3C 算法学习到的值非常接近最优策略值，并优于DROO、Dyna 框架所学习到的值，并在高任务到达速率时，每消耗总能量能达到2～3 倍简单策略所能达到的任务处理数量。

因此，所提任务处理机制具有更高的能量效率。最优策略由于需要了解信道转换概率和数据包到达率，在实际应用中可能不可行，A3C算法不需要获得相应转换概率却仍然能获得近似最优的任务处理量。

图7 表示了相较于传统算法，A3C 算法带来的收敛速度上的提升。为了方便比较，在传统算法中也采用本文的任务处理机制，便于观察在能达到相同的任务处理平均能效的情况下的收敛速率。

考虑单节点的情况下AC 算法、DROO 算法、Dyna 算法以及A3C 算法收敛速度，从图中可以看出，在相同的任务处理数量以及相同的参数设置下，A3C学习到的平均能效在迭代了3000次后开始收敛，而Dyna算法学习到的平均能效收敛在7000次左右，而DROO 以及AC 算法则需要接近8200 次迭代才能收敛，从图中可以看出，A3C 算法的收敛速度相较于传统算法得到了明显的提升。各算法达到行为收敛的时间如表4所示。

从表4中亦能看出，A3C算法收敛时间快于其他算法。A3C 算法虽然提升了学习收敛速率，但在计算方面也更加复杂，A3C 算法计算复杂度为O(N)，子线程越多，收敛速度越快，但复杂度也会越大，应根据实际情况调整子线程的数量，以满足用户需求。

7 结论

本文将无线传感器网络中任务处理的能效问题建模为MDP，从物理层以及数据链路层参数最佳控制角度着眼于无线传感器将任务本地计算以及卸载到边缘进行计算过程，保证任务得到有效处理的同时近似最大化系统能效，用强化学习方法进行求解。文章比较了本文方案与其他方案的能量效率，有明显的提升。在未来的工作中，将考虑把多节点系统中节点间的独立学习扩展为联合学习以及无线传感器的能量供应情况。