上行免调度NOMA系统中基于遗传算法的扩频矩阵优化方法
2022-04-11刘惠莹何雪云孙林慧
刘惠莹 何雪云 孙林慧
(南京邮电大学通信与信息工程学院,江苏南京 210003)
1 引言
随着海量机器类通信(Massive machine-type communications,mMTC)或大规模物联网(Internet of things,IoT)成为第五代乃至以后的蜂窝系统关键应用场景之一[1],免调度非正交多址接入(Non-Orthogonal Multiple Access,NOMA)[2]系统因其在信令开销、系统容量方面的优势而引起广泛关注。在上行免调度NOMA 场景下,文献[3]基于活跃用户集动态变化的假设,利用相邻时间段的传输数据相关性提出一种改进子空间追踪算法来解决联合信道估计(Channel Estimation,CE)和多用户检测(Multiuser Detection,MUD)问题;文献[4-5]构造稀疏帧结构传输模型且假设一帧时间内活跃用户集不变,在多重测量矢量压缩感知(Compressive Sensing,CS)[6-7]框架下各自提出重建算法来解决联合CE 和MUD 问题。文献[5]由于采用高斯随机矩阵作为扩频矩阵,系统性能有待提升。本文提出一种基于遗传算法[8]的扩频矩阵优化方法来获得优化的部分傅里叶矩阵,仿真结果表明,使用优化的部分傅里叶矩阵与使用文献[5]中的高斯随机扩频矩阵相比,可以在不增加扩频序列长度的情况下提高NOMA系统的信道估计和多用户检测性能。
在基于多重测量矢量CS 框架的免调度NOMA系统中,扩频矩阵正好对应于压缩感知模型中的恢复矩阵。我们可以利用压缩感知中的恢复矩阵优化准则来对NOMA 系统中的扩频矩阵进行优化。判断一个恢复矩阵能否很好地重建稀疏信号,目前已有一些经典判定准则:Candes,Tao 等学者提出的有限等距性质(Restricted Isometry Property,RIP)[9-10]准则;Donoho 等学者在文献[11]中提出的比RIP 更易于实现的判定准则,文中定义了恢复矩阵互相关的概念,并且得出互相关值越小越利于稀疏信号重建的结论。为了实现的方便,本文选择最小化恢复矩阵互相关准则,利用遗传算法选出合适的部分傅里叶矩阵来作为扩频矩阵。文献[12]采用同样的思路优化MIMO-OFDM 系统中用于信道估计的导频符号位置。作者将傅里叶矩阵的行间隔作为构造个体的基因对象,且为了提高遗传算法的搜索能力提出一个“完善操作”:对每次迭代得到的前十个最优个体的个别基因再次变异,以此来寻找更优个体。由于文献[12]的个体构造方法在遗传算法搜索过程中容易产生超出行索引范围的无效个体,本文的遗传算法在沿用“完善操作”的同时,提出一种“按组编码”的个体构造方式,避免了无效个体的产生,搜索性能明显提升。
2 基于多重测量矢量CS 框架的免调度NOMA系统模型
假定在免调度NOMA 系统的上行信道中基站与用户均为单天线,用如图1 所示的稀疏帧结构传输模型来传输数据。图1 中N表示发送端用户总数,在一帧的Jd+1 个时隙中,第1 个时隙用来发送导频向量xp=(xp,1,xp,2,…,xp,N)T,剩余Jd个时隙分别用来发送数据符号向量其中第j个时隙的数据符号向量表示为任意一个白格表示对应时隙的对应用户为非活动状态,在帧结构中默认发送符号为0。从图1 中可以看出在一帧时间内,只有部分用户是活跃的,且用户状态在一帧中保持不变。
假定信道为平坦瑞利衰落,扩频序列的扩展因子为M,若设发送导频符号均为1,则导频段接收信号对应的测量矩阵即为扩频矩阵,此时导频段与数据段的接收信号可以合并表示,具体表达式如下:
式中,S∈CM×N,X∈CN×J,Z∈CM×J,Y∈CM×J,其中J=Jd+1。由于h与具有相同的支撑集,若用户k处于激活状态,则向量h与的第k行将为非零值,否则将均为零值。因此式(2)建模为一个多重测量矢量CS 模型,矩阵X各列具有联合稀疏性,稀疏度等于激活用户的数量。而扩频矩阵S对应于压缩感知理论中的恢复矩阵,下面我们提出一种遗传算法对矩阵S进行优化,优化的准则就是最小化恢复矩阵互相关值。
3 基于遗传算法的扩频矩阵优化方法
在遗传算法中首先要确定适应度函数的形式和选择编码方式(即个体构造方式)。
由最小化恢复矩阵互相关准则可知,在压缩感知中,恢复矩阵的互相关值μ{S}越小,越利于精准重建稀疏信号。本文遗传算法的目标就是寻找到互相关值μ尽可能小的扩频矩阵,故定义适应度函数为扩频矩阵互相关值μ的倒数。其中互相关值μ{S}定义如下:
其中,N是恢复矩阵S的总列数,si表示S的第i列,而‖si‖则表示对si求单位l2范数。
关于编码方式,文献[12]提出固定选择傅里叶矩阵第一行,用两两之间的行间隔来进行编码,比如抽取傅里叶矩阵的1,4,8,14,19,27行,则编码为34658,编码位数总是比抽取的行数少一。由于此种编码方式只对行间隔的值进行约束,在最后映射到对应行索引时,可能会出现超过傅里叶矩阵行索引范围的值,此时该个体即为无效个体。
为了避免无效个体的产生,提高遗传算法搜寻效率,本文提出一种按组编码的个体构造方式,具体步骤如下:
1)将一个N行N列的傅里叶矩阵W的所有行索引打乱分成L组,每组分到的行索引数量相等,记为T,T=将第i组行索引构成的集合表示为Bi={bi1,bi2,…,biT},其中bit是矩阵W的某一行索引,i=1,2,…,L,t=1,2,…,T。
2)为了得到一个M行N列的扩频矩阵,需要从每组分到的行索引中各抽取a=M/L个行索引。对从Bi的T个元素中抽取a个元素的g=种可能结果进行数字编码,记为1,2,…,g。
3)在B1,B2,…,BL中都进行抽取a个元素的操作,并对抽取结果进行编码,编码结果用集合φ={φ1,φ2,…,φL}表示,其中φi为区间[1,g]内的整数,表示集合Bi的抽取结果编码。最终构成的集合φ就是遗传算法的一个个体。
完整的遗传算法步骤如下:
1)遗传算法初始化。设置参数:种群尺寸Ps,个体长度Len=L,初始迭代次数iter=1,用按组编码的个体构造方式随机生成Ps个个体,构成初始种群{φi,i=1,2,…,Ps}并计算每个个体的适应度f,将最大的适应度及其对应个体分别保存在变量fm和向量Fm中。
2)执行遗传算法的采样选择、离散重组、基因变异操作。其中个体被选择的概率Sprob=0.9,个体对间重组概率Cprob=0.7,基因变异概率Mprob=0.006 且变异的边界范围设置为1 ≤φi≤g。
3)计算得到的子代个体适应度,用基于适应度的方法将所有个体插入当前种群代替最不适应的父代个体,获得一个尺寸仍为Ps的新种群。
4)执行“完善操作”。选择当前种群适应度最大的前10 个个体和Fm中保存的个体,对每个个体进行以下操作:
a)在个体包含的L个编码结果中选出最大和最小的编码,再将最大编码分别减小1,2,3,4,同时将最小编码分别增大1,2,3,4,获得4个新个体;
b)在个体包含的L个编码结果中随机选择一个,将其分别增大和减小1,2,3,获得6个新个体;
c)在原个体和其新生的10个个体中,选择适应度最大的个体来取代原个体。
5)计算当前种群中所有个体以及Fm中保存个体的适应度,选择最大适应度个体更新fm和Fm。
6)判断是否停止迭代:当fm累计不变次数达到λ,进入步骤7),否则,iter=iter+1,进入步骤2)。
7)由Fm中的L个编码值映射到L个组的行索引抽取结果,再根据得到的个行索引提取出傅里叶矩阵W的对应行,将其按行拼接成M×N的部分傅里叶矩阵,即扩频矩阵Sopt。
虽然在步骤2)中由于编码方式的特点不会产生无效个体,但是在步骤4)的完善操作中,随着对个体基因的增加/减小,可能会出现基因值大小超出有效范围的情况,此时需要对在有效范围外的基因值进行±g的操作使其回到有效范围。在步骤6)中,将每次迭代后的fm与前次进行比较,若保持不变,则fm累计不变次数加1;若发生改变,则fm累计不变次数归为1。当fm累计不变次数达到λ,则停止迭代,其中λ为设置的停止迭代阈值。
4 仿真结果和分析
本文仿真分为两部分:第一部分用本文提出的遗传算法对NOMA 系统的扩频矩阵进行优化,第二部分基于文献[5]中的系统模型和所提算法,仿真分析使用我们优化后的扩频矩阵相对于文献[5]中使用的高斯随机矩阵所带来的性能改善。各项仿真均是在有4 GB RAM 和2.3 GHz 的Inte(lR)Core(TM)I5-6200U CPU 的联想笔记本上运行Matlab2018a 完成的。
4.1 遗传算法仿真结果分析
本节以优化维度为32 × 256 的扩频矩阵为例,比较以下三种算法可获取的最小互相关值μ的大小以及算法收敛性:(1)按行间隔编码经典遗传算法;(2)文献[12]提出的带“完善操作”的按行间隔编码遗传算法;(3)本文提出的带“完善操作”的按分组编码遗传算法。仿真过程中,三种遗传算法以下参数设置均相同:种群大小Ps=100,个体被选择的概率Sprob=0.9,个体对间重组概率Cprob=0.7,基因变异概率Mprob=0.006,迭代停止的门限值λ=300。
在按组编码遗传算法中,将傅里叶矩阵W∈C256×256的行索引集合{1,2,…,256}中元素随机均分为L=32 组,则每组有T=256/32=8 个行索引,为了最后能够拼成维度为32 × 256 的部分傅里叶矩阵,我们需要在每组的8 个行索引中选择a=32/32=1 个行索引,共有g==8 种可能选择结果。所以个体长度Len=L=32,基因变异边界范围1 ≤φi≤8。而其余两种按行间隔编码的遗传算法中,个体长度设置为31,基因变异边界范围设置为[3,15]。
三种算法在不同迭代次数下的互相关值的大小分布如图2 所示,从获得的矩阵最小互相关值大小来看,经过数次迭代,三种算法获得的扩频矩阵互相关值分别为0.3037、0.2954 和0.2584。结果表明“完善操作”能使得算法获得更低的互相关值,因为它加大了遗传算法的搜索范围;在同样进行“完善操作”的情况下,按组编码遗传算法比按行间隔编码性能更好。原因如下:第一,按行间隔编码遗传算法在基因变异及完善操作中均可能产生无效个体,影响搜索效率,而按组编码遗传算法只在完善操作部分产生少数无效个体,且通过指定操作可将其恢复成有效个体;第二,按行间隔编码固定了傅里叶矩阵的第一行,相比而言,按组编码使得遗传算法有更大的搜索自由和搜索空间。从算法收敛角度来看,遗传算法在设计时应尽量避免过早收敛导致的“早熟”。在本小节提到的三种遗传算法中,按行间隔编码经典遗传算法、带“完善操作”的按行间隔编码遗传算法、带“完善操作”的按组编码遗传算法收敛速度依次变慢,本文提出来的遗传算法能够通过更多次迭代找到更小的互相关值。
4.2 扩频矩阵在稀疏信号重建算法中的性能分析
本节在文献[5]系统模型下分别使用高斯随机矩阵和优化后的部分傅里叶矩阵作为扩频矩阵,运行文献[5]提出的算法观察二者性能差异。仿真参数设置如下:扩频序列长度为M=32,潜在用户数N=256,活动用户数K=16;在一帧7 个时隙中导频数据占1 个时隙,数据信息发送占6 个时隙;信道为平坦瑞利衰落信道;调制方式为QPSK。算法中参数设置同文献[5],μ值为0.085,阈值参数α=0.9。最终的仿真结果是在5 dB、10 dB、15 dB、20 dB、25 dB、30 dB的信噪比情况下均运行2000次,取平均值,其中不同信噪比对应的算法迭代终止门限值分别设置为0.21、0.07、0.035、0.014、0.0035、0.0014。
本文通过以下四个性能指标来比较系统分别使用优化后的部分傅里叶矩阵和高斯随机矩阵作为扩频矩阵时,系统性能的差别:误符号率(Symbol Error Rate,SER)、成功活跃检测率(Successful Activity Detection Rate,SADR)、归一化均方误差(Normalized Mean Square Error,NMSE)及信道估计和多用户检测算法运行时间。另外,针对前三个性能指标,还比较了使用经典遗传算法获得的扩频矩阵以及使用本文提出的改进遗传算法获得的扩频矩阵二者在性能上的差异。
4.2.1 SER性能分析
本小节比较系统在使用不同扩频矩阵情况下的误符号率性能。
表1给出了系统使用不同遗传算法获得的优化扩频矩阵时的SER 性能,仿真结果表明使用本文所提算法优化获得的扩频矩阵能够使得系统获得更低的SER值。

表1 不同信噪比条件下使用两种部分傅里叶扩频矩阵的SER值比较Tab.1 The Comparison of SERin the case of two partial Fourier spread spectrum matrix under different SNR
接下来对系统使用本文所提遗传算法优化获得的扩频矩阵和使用文献[5]中的高斯随机扩频矩阵的误符号率性能进行比较。仿真结果如图3 所示,在信噪比分别为5 dB、10 dB、15 dB、20 dB、25 dB、30 dB 的情况下,随着信噪比的增加,系统使用优化后的部分傅里叶扩频矩阵,相比使用高斯随机扩频矩阵,误符号率下降越多。比如当信噪比为10 dB 时,使用优化后的部分傅里叶扩频矩阵得到的系统SER 值为2.891 × 10-2,相比使用高斯随机扩频矩阵得到的系统SER值3.955×10-2,降低了26.9%;而当信噪比为25dB时,使用优化后的部分傅里叶扩频矩阵得到的系统SER 值为4.307 × 10-3,相比使用高斯随机扩频矩阵得到的系统SER 值1.589 × 10-2,降低了72.89%。考虑所有信噪比取值时的仿真结果,使用本文所提遗传算法优化的扩频矩阵得到的系统SER值平均降低了52.14%。
4.2.2 SADR性能分析
本小节比较系统在使用不同扩频矩阵情况下的成功活跃检测率,即正确检测出来的活动用户数与总的活动用户数之比。
表2给出了系统使用不同遗传算法获得的优化扩频矩阵时的SADR 性能,仿真结果表明使用本文所提算法优化获得的扩频矩阵能够使得系统获得更高的SADR值。
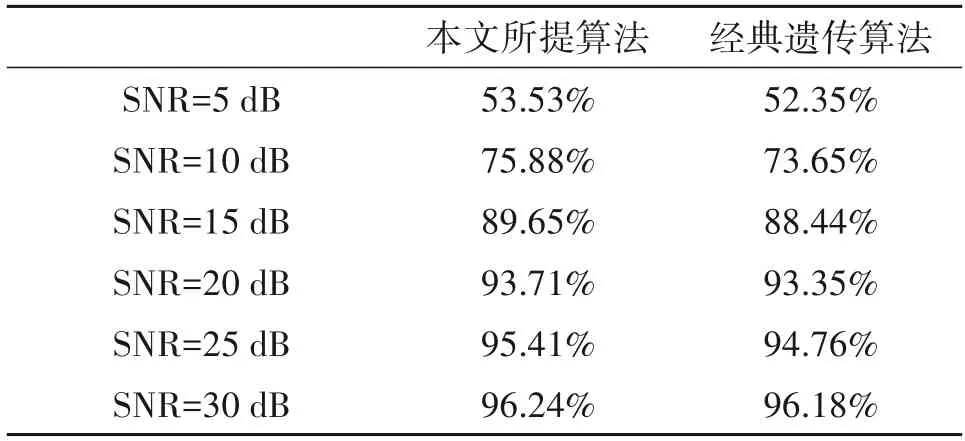
表2 不同信噪比条件下使用两种部分傅里叶扩频矩阵的SADR值比较Tab.2 The Comparison of SADR in the case of two partial Fourier spread spectrum matrix under different SNR
接下来对系统使用本文所提遗传算法优化的扩频矩阵和使用文献[5]中的高斯随机扩频矩阵的成功活跃检测率性能进行比较。仿真结果如图4 所示,在信噪比分别为5 dB、10 dB、15 dB、20 dB、25 dB、30 dB 的情况下,系统使用优化后的部分傅里叶扩频矩阵均能得到更高的SADR值。比如当信噪比为15 dB 时,使用优化后的部分傅里叶扩频矩阵得到的系统SADR 值为87.19%,相比使用高斯扩频矩阵得到的系统SADR 值为72.59%,提高了14.6%。考虑所有信噪比取值时的仿真结果,使用本文所提遗传算法优化的扩频矩阵得到的系统SADR 值平均提高了12.14%。
4.2.3 NMSE性能分析
本小节比较系统在使用不同扩频矩阵情况下的信道估计性能。若用h表示信道系数向量,h^ 表示信道系数向量估计值,G表示仿真次数,则信道估计的归一化均方误差NMSE表示如下:
表3给出了系统使用不同遗传算法获得的优化扩频矩阵时的NMSE 性能,仿真结果表明使用本文所提算法优化获得的扩频矩阵能够使得系统获得更低的NMSE。
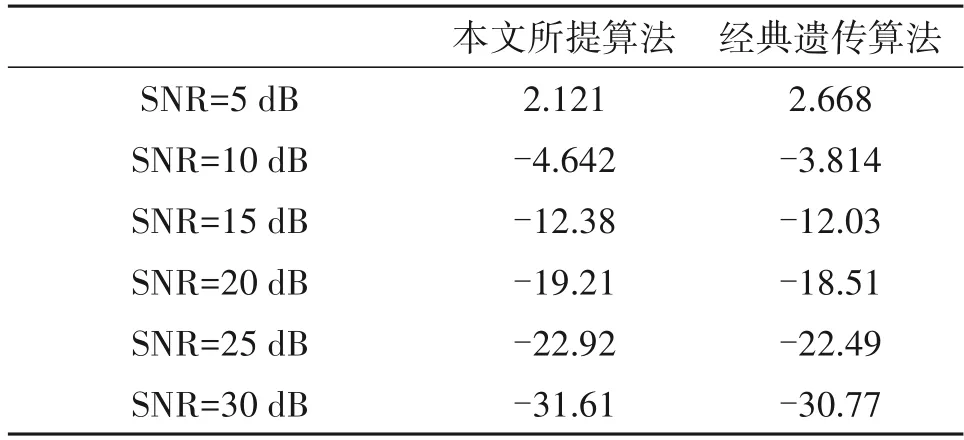
表3 不同信噪比条件下使用两种部分傅里叶扩频矩阵的NMSE值比较(单位:dB)Tab.3 The Comparison of NMSE in the case of two partial Fourier spread spectrum matrix under different SNR(unit:dB)
接下来对系统使用本文所提遗传算法优化的扩频矩阵和使用文献[5]中的高斯随机扩频矩阵的信道估计性能进行比较。最终的仿真结果如图5所示,在信噪比为5 dB、10 dB、15 dB、20 dB、25 dB、30 dB 时,系统使用优化后的部分傅里叶扩频矩阵均能得到更低的NMSE 值。比如在信噪比为20 dB处,使用优化后的部分傅里叶扩频矩阵得到的系统NMSE 值为-14.37 dB,相比使用高斯随机扩频矩阵得到的系统NMSE 值-2.476 dB,降低了11.894 dB。考虑所有信噪比取值时的仿真结果,使用本文所提遗传算法优化的扩频矩阵得到的NMSE 约降低10 dB左右。
4.2.4 运行时间比较
本小节比较系统在使用不同扩频矩阵情况下,基于不同信噪比运行2000 次后的信道估计和多用户检测平均每次运行时间。
仿真结果如图6所示,在所有信噪比条件下,系统使用优化后的部分傅里叶扩频矩阵均得到更少的平均运行时间。比如在25 dB 处,使用优化后的部分傅里叶扩频矩阵得到的平均运行时间为0.0308 s,相比使用高斯随机扩频矩阵的平均运行时间0.0418 s,减少了0.011 s。考虑所有信噪比取值时的仿真结果,使用本文所提遗传算法优化后的扩频矩阵得到算法的平均运行时间,相比使用高斯扩频矩阵,平均减少了0.0116 s。另外,使用不同遗传算法优化获得的扩频矩阵时,系统信道估计和多用户检测所花时间基本一致。
5 结论
本文提出了一种基于遗传算法的部分傅里叶矩阵优化方法来解决上行免调度NOMA 系统中的扩频矩阵设计问题。与解决同类问题的遗传算法不同之处是——我们提出了一种按组编码的新个体构造方式:将傅里叶矩阵行索引随机均分成L组,从每组选出数量固定且相等的若干索引,分别对每组内所有可能出现的选择结果用码字1,2,3,…表示,并依此对L个组的选择结果进行编码,从而构成遗传算法的个体。仿真结果表明,在基于多重测量矢量CS 框架下的NOMA 系统中,使用优化后的部分傅里叶矩阵作为扩频矩阵,相比高斯随机扩频矩阵,能够获得更优秀的激活用户联合数据检测和信道估计性能,且运行时间大大减少。
