小波分析辅助GPS-R潮位反演

明 眉，岳东杰，朱少林

小波分析辅助GPS-R潮位反演

明 眉，岳东杰，朱少林

(河海大学 地球科学与工程学院，南京 211100)

针对使用全球定位系统反射信号测量技术（GPS-R）分离海面直射信号时，低高度角情况下、低阶多项式方法容易出现偏差的问题，提出了一种利用小波分析方法去除直射信号的海面潮位反演算法。通过美国华盛顿州SC02测站2016年年积日（DOY）第92—97天连续6 d观测数据进行验证，结果表明，使用改进的小波分析方法，能够更好地拟合信噪比变化情况，获得更高精度的卫星反射信号；潮位反演精度在L1波段有较小的降低，而在L2波段反演精度有明显的提升。

全球定位系统；小波分析；潮位监测；信噪比；卫星反射信号

0 引言

全球气候变暖现象带来的冰川融化、海平面高度上升，使得潮位监测变得更加重要。传统的潮位监测方法是通过验潮站的验潮仪和水尺来记录来潮位变化的，但由于地壳运动的影响，结果存在误差，卫星测高作为监测潮位的另一种方法，可以以较高的精度实现大范围潮位监测，但是在近海区域，因受海岸影响，其监测精度较低。全球定位系统反射测量技术（global positioning system reflectometry，GPS-R）是一种利用全球定位系统（global positioning system, GPS）卫星反射信号的波形、幅值、相位和频率等参量的变化，来反演反射面物理特性的技术。目前在雪深探测、反演土壤湿度、植被变化、风暴潮等多个领域得到了广泛的应用，并取得了较高的监测精度[1-4]。GPS-R技术在监测地球表面物理特性方面，具有全天候、成本低、信号资源丰富等优势，得到了国内外学者的广泛关注。GPS-R技术在潮位监测方面，已经取得了不少研究成果。文献[5]利用GPS-R技术在湖面开展了水位测量研究工作，实验结果表明可以获得±3 cm的水位监测精度[5]。文献[6]使用单颗卫星信噪比（signal-to-noise ratio，SNR）观测值，研究海平面潮位变化，获得了±27 cm的监测精度[6]。文献[7]为了获取测站1 d、15 d、1 a的潮位变化，对岸基连连续运行参考站（continuously operating reference stations, CORS）的信噪比观测数据进行处理，结果表明全球卫星导航系统反射测量技术(global navigation satellite system reflectometry，GNSS-R)得到的潮位信息与验潮站实测值高度相关，较差约为10 cm[7]。文献[8]利用小波分解方法提取海面反射信号，去除其他信号对反演潮位的影响；文献[9]利用经验模态分解方法分析信噪比数据，提取反射信号，试验结果验证了这两种方法均在一定程度上提高了反演潮位的精度。文献[10]提出基于小波分析原理的卫星反射信号分离模型，卫星反射信号的分离精度能够得到有效提高，提高了土壤湿度的反演精度[10]。文献[11]使用小波分析的方法对采集的大洋山单天线GNSS信号数据进行处理，主要使用小波去噪方法，处理了含噪声源的信号，实验结果证明了小波分析方法的可靠性与有效性[11]。文献[12]提出利用小波变换分析方法获取GNSS信噪比序列的瞬时频率，从而获得瞬时潮位值，实验结果表明，小波分析方法反演潮位值的精度能达分米级，并且反演潮位时间分辨率优于经典法和加窗法，但是这种方法不能脱离经典法单独使用[12]。

在以往使用GNSS-R反演潮位的研究中，通常使用低阶多项式拟合的方法去除直射信号，这种方法的优点是整体拟合性较好，分离直射信号后的反射信号，其反演潮位精度可达分米级。但是低阶多项式方法在分离直射信号时，没有充分考虑可能存在的部分时段拟合不准确的问题。小波分析能够在时域和频域方面同时局部化的特点，已经在图像去噪、获取信号趋势等领域得到了广泛的应用[10]，文献[10]将小波分析的分离方法应用于土壤湿度反演分析，没有考虑不同频率波段对SNR序列反演结果的影响。本文通过小波分析方法，去除信噪比数据序列中的直射信号分量，以获得高精度的卫星反射信号，实现高精度的GPS-R潮位反演。本文以美国华盛顿州弗赖迪港（Friday Harbor）的SC02测站观测数据为例，分别处理L1波段和L2波段的观测数据，反演获得高精度的潮位信息。

1 原理与方法

1.1 GPS-R反演水面高度原理

在一般GPS定位测量中，多路径效应作为影响GPS定位精度的主要误差源，需要尽可能地降低其影响，但是在GPS-R应用中，因为多路径效应的存在，导致单天线卫星接收机中接收到的信号实际上是直射信号和反射后的合成信号[13]。

信号质量通常是用信噪比来衡量，当信号功率为P，而噪声功率为时，信噪比表示为

式中，NR为信噪比值，单位为dB。在使用信噪比值反演潮位时，需要对其进行单位转换，转换为线性单位（V·V-1）为

图1为PRN20卫星多路径值和信噪比值随着卫星高度角变化的情况。

图1 PRN20卫星的高度角、多路径值和信噪比值变化

由图1可得，随着高度角的增加，多路径效应降低，但在低高度角时，反射信号更容易被接收机接收，从而使得多路径效应明显，直射信号和反射信号的干涉现象突出，信噪比值有明显的振荡。

涅温斯基（Nevinski）和克拉尔松（Larson）提出一种近地面直射反射组合信号功率表达式[14]，即

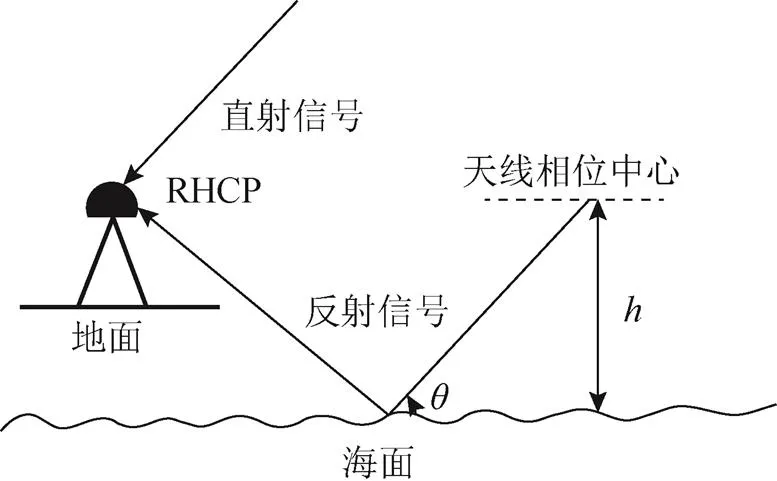
图2 GPS-R反演海面高度原理

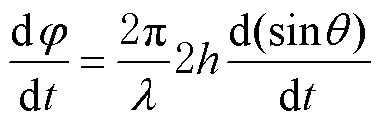
文献[15]研究发现，卫星反射信号与高度角存在的正（余）弦关系[15]为

式（8）的频率可以通过对反射信号进行频谱分析获得，这里的反射信号是指原始信噪比数据，经分离直射信号后的SNR残差序列，也就是式（7）中的NRm。对NRm频谱分析时，自变量为高度角正弦值，为非均匀采样，使用传统的快速傅里叶变换(fast Fourier transform，FFT）无法分析，所以本文使用洛姆-斯卡格尔周期图（Lomb-Scargle periodogram, LSP）谱分析方法来分析NRm，获得反射信号的主频率，根据式（8）计算得到水面到接收机天线的垂直反射距离。LSP谱分析处理的信号是经直射分量分离后的NRm，可见现在利用卫星反射信号获取海面高度时，直射信号的分离很重要。

潮位反演过程中，分离直射信号常用的方法是使用低阶多项式拟合趋势项，去除直射信号分量，这种方法的缺点是简单地认为直射信号在SNR序列中呈现出二阶多项式趋势，没有考虑这种方式是否会去除序列中的有用信息。因此，采用二阶多项式拟合的方法，可能可能会出现计算模型偏离实际的情况。

1.2 小波分解原理

格罗斯曼（Grossmann）提出的小波变换分解方法，是对满足条件的信号使用不同尺度函数逐次逼近，获得一系列近似表达式，得到多尺度平滑信号表达式，不同的尺度对应不同的频率[16]。在反演水面高度问题中，信号为SNR序列，对小波分解后得到的小波系数进行重构，可以分别得到信号的低频和高频部分，分解算法[17-18]为

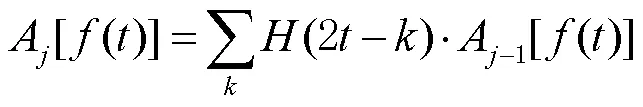
式中：和为重构小波滤波器；A为重构得到的低频信号。

2 实验分析

2.1 试验数据及方案

本文选取布设在美国华盛顿州SC02站，2016年年积日（day of year, DOY）第92—97天的数据进行分析，该站属于板块边界观测（plate boundary observatory，PBO）网络计划项目。SC02测站周边环境如图3所示，站点安装天宝（Trimble）NETRS接收机，并配备Trimble TRM29659.00天线，本文选择距离该测站359 m的Friday Harbor验潮站验潮仪每6 min获取的实测数据作为参考数据。利用SC02站的GPS L1波段和GPS L2波段观测数据，设计两种试验方案对比分析不同方法反演水位的精度：1）低阶多项式拟合方法分离直射信号；2）小波分解方法分离直射信号。

图3 SC02站的环境

由于测站观测数据L1波段和L2波段观测质量不同，L1波段的观测质量较好，多路径效应影响较低，SNR值较大，而L2波段则反之；所以分别使用L1和L2波段的观测数据进行海面潮位反演。

2.2 反演精度分析

首先通过尔特克利布（RTKLIB）软件对导航文件和测站观测文件进行处理分析，分别获得L1波段和L2波段的高度角、方位角以及SNR观测值信息。卫星高度角和方位角范围的选择，对反演精度的影响较大。为了获得更高时间分辨率的反演结果，结合SC02测站的实际观测环境，本文选择的高度角区间为5～13°，方位角区间为50～240°。首先对SC02测站观测数据进行筛选，区分观测序列的上升弧段和下降弧段，从而得到符合条件的SNR序列。在获得SNR序列后，根据反演潮位的处理步骤，分别使用低阶多项式拟合和小波分析分离直射信号，获得反射信号NRm序列。然后对得到的NRm进行LSP谱分析，获得主频率，根据频率与反演高度的关系求得反演高度。最后统一验潮站和SC02站的高程基准，将反演高度转换到验潮站的高程基准。图4为信噪比反演潮位信息处理流程图。

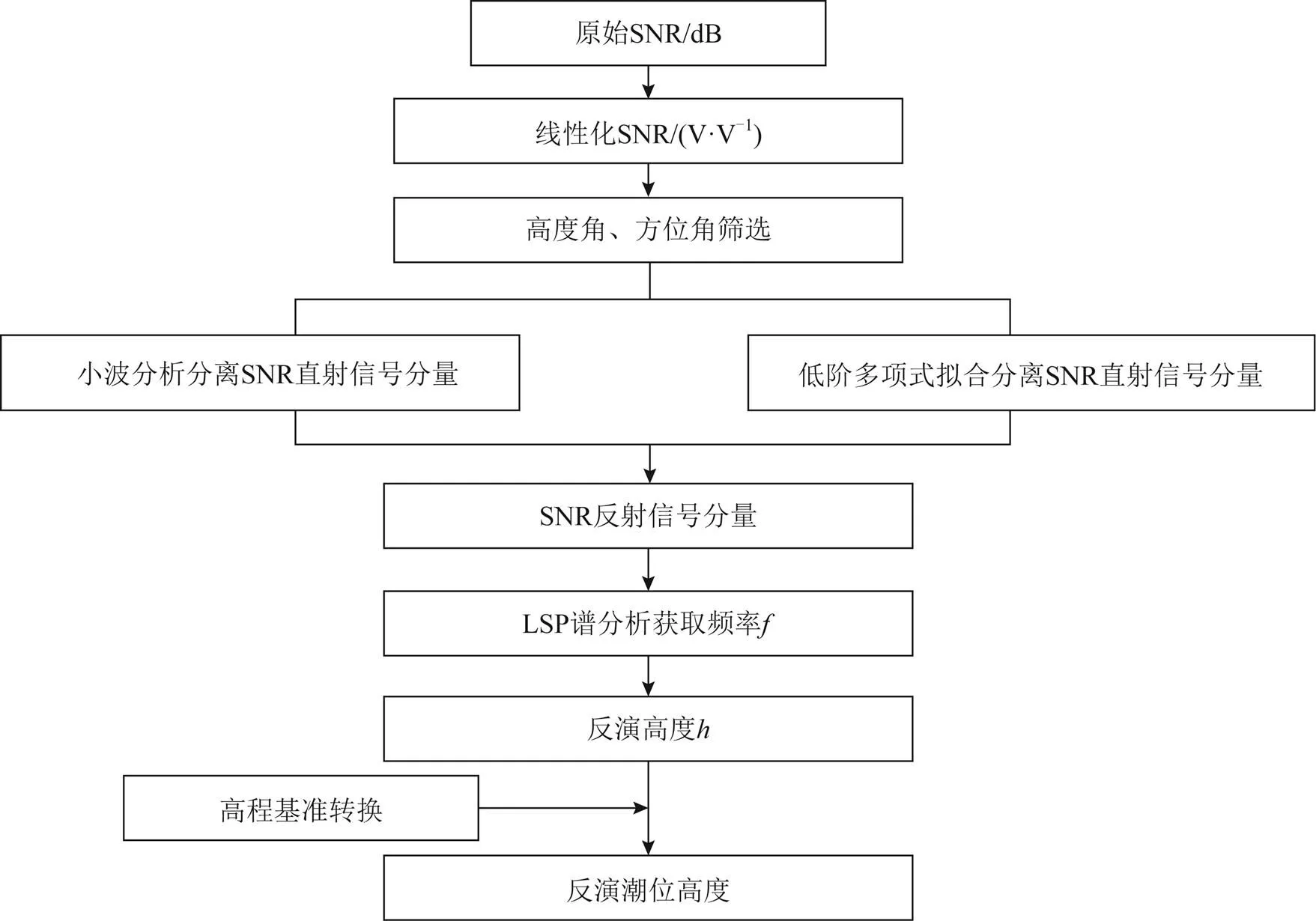
图4 信噪比反演潮位信息处理流程

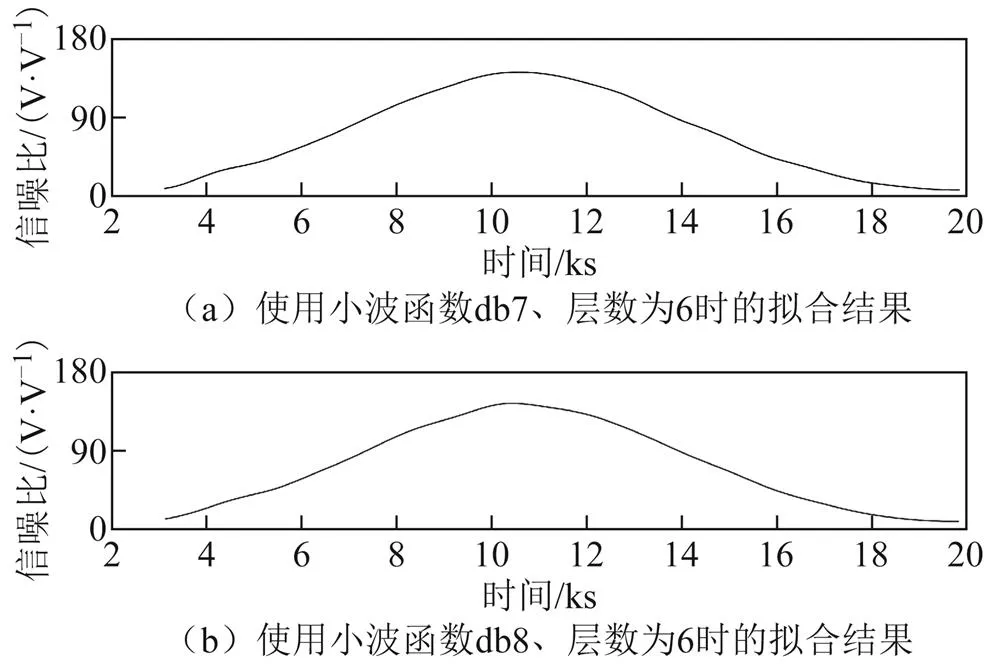
小波分析获取趋势项的关键在于小波函数和层数的选取。因此，先通过多次实验分析，选择最优的小波函数和层数。不同的小波函数和层数拟合趋势项的结果如图5和图6，图5为使用不同小波函数、层数为6，拟合信噪比序列趋势项的结果，图6为使用小波函数db10，不同层数拟合信噪比序列趋势项的结果。使用不同小波函数和层数拟合趋势项，根据潮位反演流程计算反演潮位值。经比较得出，使用小波函数db10，层数为6时，反演结果精度最可靠。

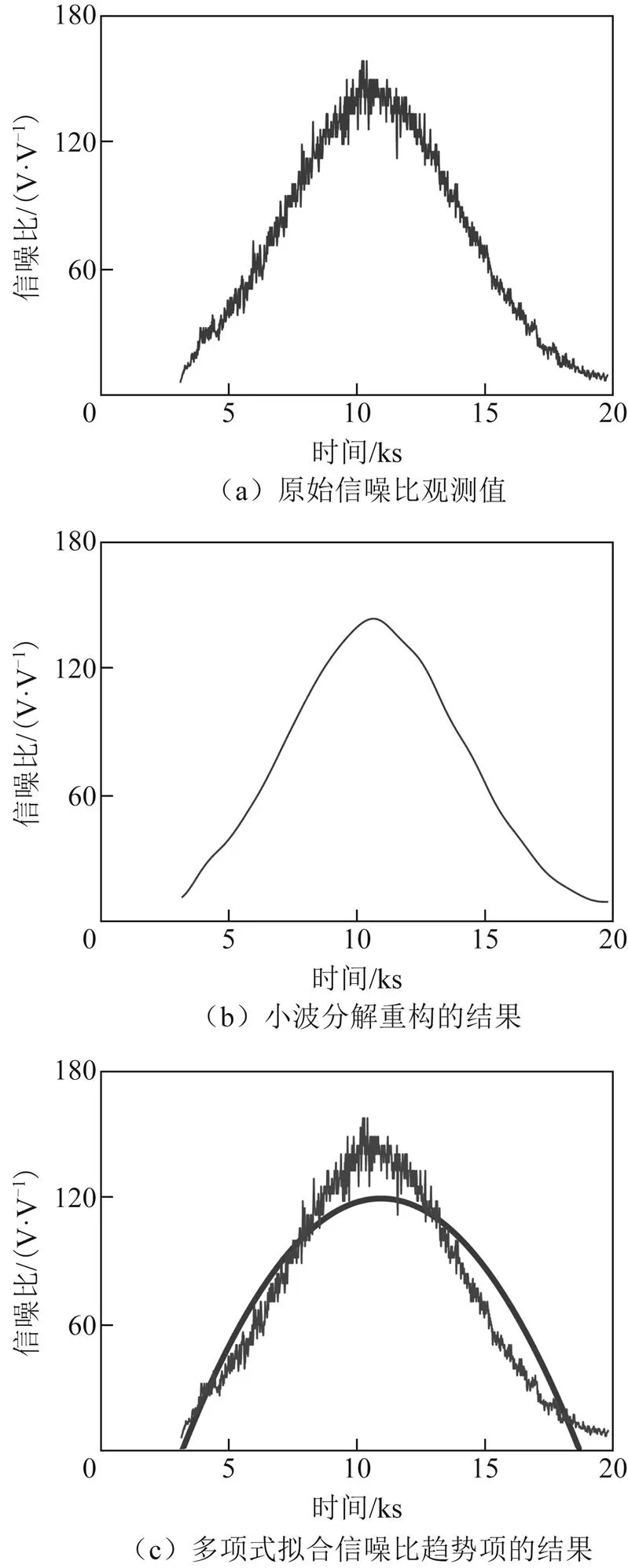
使用小波函数db10，层数为6拟合信噪比序列变化趋势，其拟合结果见图7。图7（a）为一段历元信噪比原始观测值序列，图7（b）为使用小波分解重构趋势项得到的结果，图7（c）为使用二阶多项式拟合得到的结果，图7（d）为使用小波分析拟合得到的结果。对比分析可以得出，采用低阶多项式方法拟合时，在低高度角时出现了明显的偏差，不能准确地反映信噪比的变化情况，而小波分析可以很好地反映序列变化趋势，在低高度角区间，也能更好地拟合信噪比序列。

对L1波段和L2波段的SNR序列进行处理，获得两个频率波段的潮位反演结果，并采用均方根误差（root mean square error, RMSE）和平均绝对值误差（mean absolute error, MAE）进行精度评价，RMSE和MAE的计算公式为

为了评价反演潮位值的精度，将验潮站验潮仪获得的潮位值与反演得到的潮位值之差作为较差，限于篇幅，只随机给出2016年年积日第93天L1波段和L2波段部分时刻，使用不同方案的反演结果。表1为L1波段反演潮位较差对比结果，表2为L2波段反演潮位较差对比结果，表中时间系统使用的是协调世界时（universal time coordinated，UTC）。可以看出，使用小波分析分离直射信号的方法处理L1波段数据时，反演结果精度并没有明显提升，而且部分时刻误差有所增大；而处理L2波段数据时，结果精度有明显提升，粗差的数量也有所降低。

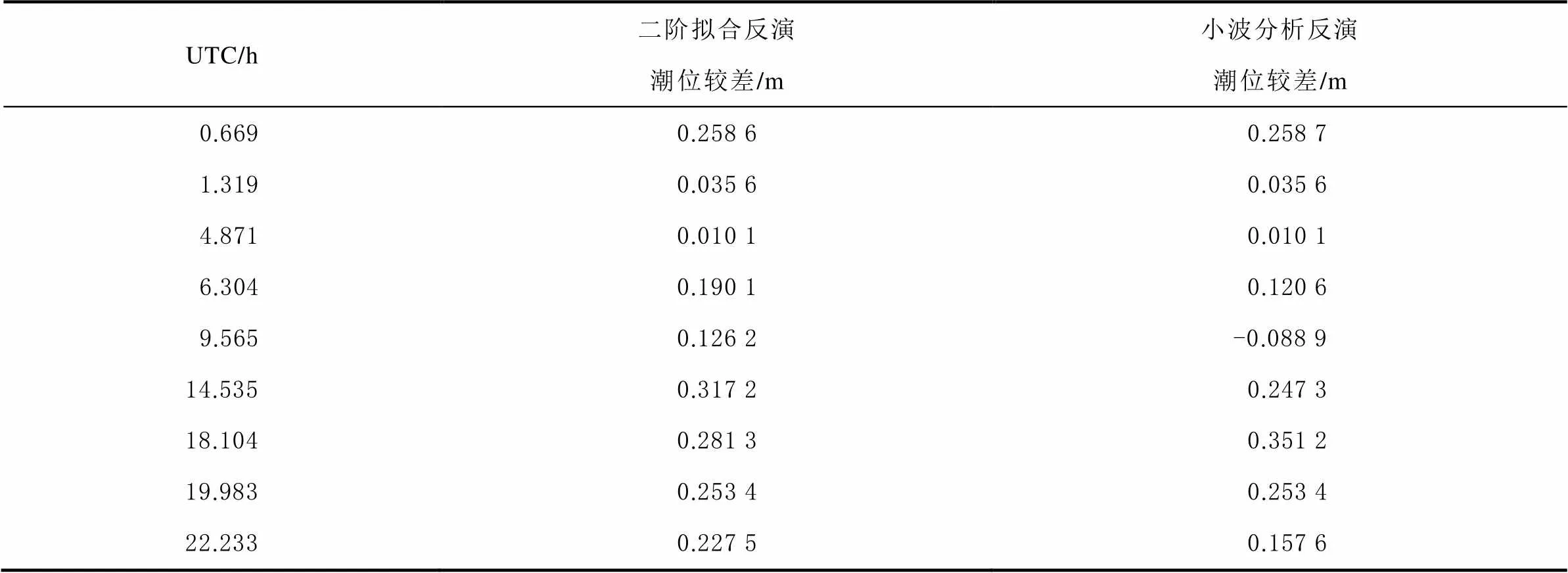
表1 L1波段反演潮位较差统计

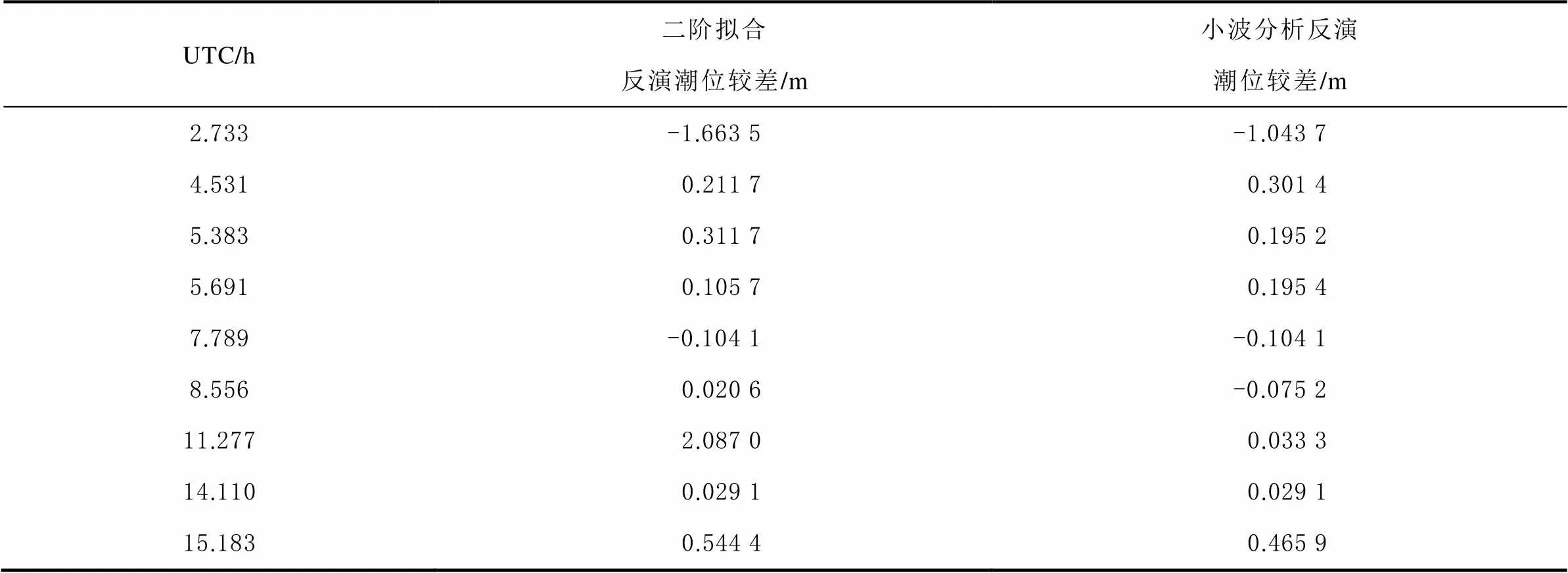
表2 L2波段反演潮位较差统计

表3为L1波段分别采用二阶拟合方法和小波分析方法去除直射信号的6 d反演结果精度，表3中每一天的均方根误差和平均绝对误差是通过将这一天的全部时刻反演潮位结果，根据其公式计算得到的。由于L1波段的SNR值较大，多路径效应影响较低，使用不同方法分离直射分量，对结果精度的影响不明显，但统计6 d的数据得出，小波分析分离直射信号得到均方根误差总体提高了5.98%，平均绝对误差总体提高了5.45%，精度总体上呈下降趋势。表4为L2波段不同年积日分别使用二阶拟合和小波分析方法去除趋势项的反演结果精度，可以看出小波分析去除趋势项均方根误差总体上得到了降低，最高降低了39.41%，总体上降低了7.71%，平均绝对误差最高降低了25.74%，总体降低了5.94%，在反演精度较低时，使用小波分析去除趋势项，可以降低粗差的出现，大大提高反演的可靠性。从表3和表4的对比可以得出，L1波段观测数据反演潮位精度比L2波段反演潮位精度高。小波分析分离直射信号方法处理L1波段并不能使精度提高，反而会造成小幅度地降低，但是处理L2波段时，精度能够得到明显提高，所以在使用SNR数据反演潮位精度较低时，可以使用小波分析方法辅助提高反演精度。

表3 L1波段反演结果精度统计 单位：m

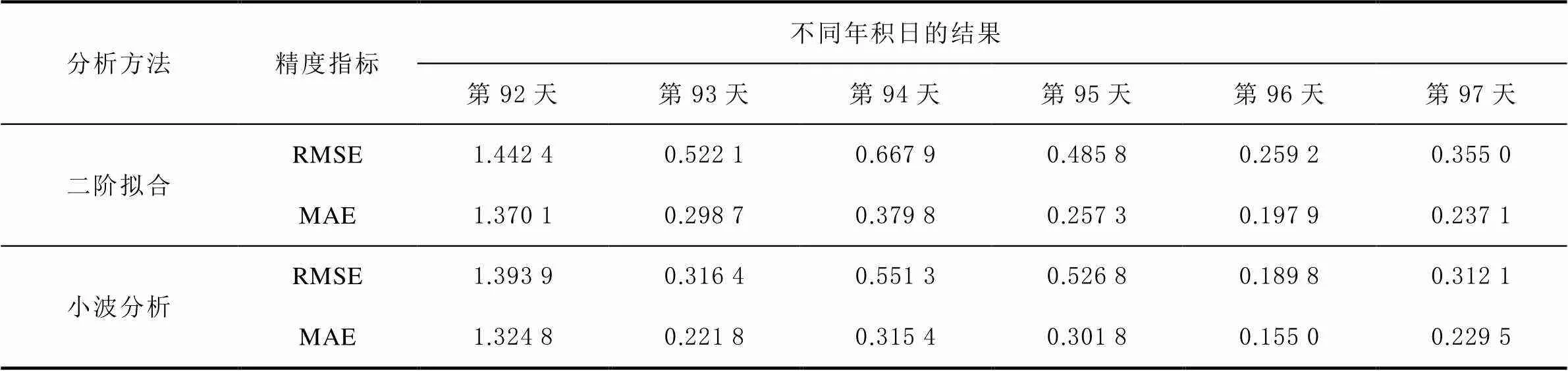
表4 L2波段反演结果精度统计 单位：m

3 结束语

本文提出了一种基于小波分析的GPS-R海面潮位反演方法，通过小波分析方法有效地分离SNR序列中的直射信号分量，以获得高精度的卫星反射信号。本文数据来自SC02站GPS L1波段和GPS L2波段的信噪比数据。在拟合SNR趋势项时，分别采用小波分析方法和二阶多项式拟合方法进行海面潮位反演。结果表明：在低高度角范围时，二阶多项式拟合方法在分离直射信号分量时，容易出现偏差；而小波分析方法可以有效地去除直射信号，能够更好地反映SNR序列的变化趋势。L1波段和L2波段SNR反演潮位的精度有较大的差别，小波分析方法对二者的潮位反演精度有不同程度的提升。小波分析方法对L1波段数据的反演结果精度降低，小波分析分离直射信号得到的均方误差总体提高了5.98%，平均绝对误差总体提高了5.45%；而对L2波段数据的反演精度有明显提升，6 d的均方误差总体降低了7.71%，其中最高可以降低39.41%，平均绝对误差总体降低了5.94%，最高降低了25.74%。下一阶段的研究将分析趋势项在不同高度角范围的变化情况，以此来确定不同高度角范围对趋势项拟合的影响。

[1] GUTMANN Ethan D, LARSON Kristine M, WILLIAMS Mark W, et al. Snow measurement by GPS interferometric reflectometry: an evaluation at Niwot Ridge, Colorado[J]. Hydrological Processes, 2012, 26(19): 2951-2961.

[2] LARSON K M, SMALL E E, GUTMANN E, et al. Using GPS multipath to measure soil moisture fluctuations: initial results[J]. GPS Solutions, 2008, 12(3):173-177.

[3] SMALL E E, LARSON K M, BRAUN J J. Sensing vegetation growth with reflected GPS signals[EB/OL]. [2021-06-16]. http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.1072.723&rep=rep1&type=pdf.

[4] PENG D, HILL E M, LI L, et al. Application of GNSS interferometric reflectometry for detecting storm surges[EB/OL].[2021-06-16]. https://dr.ntu.edu.sg/bitstream/10356/81377/1/Peng2019_Article_ApplicationOfGNSSInterferometr.pdf.

[5] 吴继忠, 杨荣华. 利用GPS接收机反射信号测量水面高度[J]. 大地测量与地球动力学, 2012, 32(6):135-138.

[6] NAKASHIMA Y, HEKI K. GPS tide gauges using multipath signatures[J]. Journal of the Geodetic Society of Japan, 2013, 59(4):157-162.

[7] 张双成, 南阳, 李振宇,等. GNSS-MR技术用于潮位变化监测分析[J]. 测绘学报, 2016(9):1042-1049.

[8] WANG Xiaolei, ZHANG Qin, ZHANG Shuangcheng. Water levels measured with SNR using wavelet decomposition and Lomb–Scargle periodogram[J]. GPS Solutions, 2018, 22(1): 1-10.

[9] ZHANG S, LIU K , LIU Q, et al. Tide variation monitoring based improved GNSS-MR by empirical mode decomposition[J]. Advances in Space Research, 2019, 63(10):3333-3345.

[10] 任超, 张志刚, 梁月吉, 等. 基于小波分析辅助GPS-IR反演土壤湿度研究[J]. 大地测量与地球动力学, 2020, 40(1): 77-81.

[11] 王杰, 何秀凤, 王笑蕾, 等. 小波分析在 GNSS-IR 潮位反演中的应用[J]. 导航定位学报, 2020, 8(2): 82-89.

[12] 苏晓容, 张云, 韩彦岭, 等. 岸基GNSS单天线潮位高度小波分析反演[J].导航定位学报,2019,7(4): 87-93.

[13] 张双成, 戴凯阳, 刘凯, 等. GPS-MR技术用于降雪厚度监测研究[J]. 地球物理学进展, 2016, 31(4): 1879-1884. DOI: 10.6038/pg20160461.

[14] NIEVINSKI F G, LARSON K M. Forward modeling of GPS multipath for near-surface reflectometry and positioning applications[J]. GPS Solutions, 2014, 18(2): 309-322.

[15] CHEW C C, SMALL E E, LARSON K M, et al. Effects of near-surface soil moisture on GPS SNR data: development of a retrieval algorithm for soil moisture[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(1):537-543.

[16] GROSSMANN A, MORLET J. Decomposition of hardy functions into square integrable wavelets of constant shape[J]. Siam Journal on Mathematical Analysis, 1984, 15(4): 723-736.

[17] 罗甘, 梁月吉, 黄仪邦. 基于双树复小波的变形监测数据去噪分析[J]. 大地测量与地球动力学, 2018, 38(9):958-963.

[18] 王旭, 王昶. 一种改进小波阈值去噪方法的研究[J]. 大地测量与地球动力学, 2011, 37(10):1038-1041.

Tide level inversion using wavelet analysis assisted GPS-R

MING Mei, YUE Dongjie, ZHU Shaolin

（School of Earth Science and Engineering, Hohai University, Nanjing 211100，China）

Aiming at the problem that the low-order polynomial method is prone to deviation when the Global Positioning System-Reflectmetry (GPS-R) technology is used to separate the direct signal from the sea surface at low altitude, a sea surface tide inversion algorithm using wavelet analysis method to remove the direct signal is proposed. The results show that the improved wavelet analysis method can better fit the change of signal-to-noise ratio and obtain more accurate satellite direct signal; the accuracy of tide level inversion is slightly reduced in L1 band, but it is improved in L2 band.

global positioning system; wavelet analysis; tide level monitoring; signal to noise ratio; satellite reflected signal

P228

A

2095-4999(2022)02-0126-08

明眉，岳东杰，朱少林. 小波分析辅助GPS-R潮位反演[J]. 导航定位学报, 2022, 10(2): 126-133.（MING Mei, YUE Dongjie, ZHU Shaolin. Tide level inversion using wavelet analysis assisted GPS-R[J]. Journal of Navigation and Positioning, 2022, 10(2): 126-133.）

10.16547/j.cnki.10-1096.20220216.

2021-07-09

明眉（1997—），女，山东菏泽人，硕士研究生，研究方向为GNSS反射信号。

岳东杰（1966—），女，山东梁山人，博士，教授，博士生导师，研究方向为测绘数据处理。