碳纳米管/碳纤维增强复合材料层合板低速冲击响应和破坏的数值模拟*
2022-04-11文鹤鸣
王 敏,文鹤鸣
(中国科学技术大学中国科学院材料力学行为和设计重点实验室,安徽 合肥 230026)
纤维增强树脂基(fibre reinforced plastics, FRP)复合材料具有比强度高、比模量高、可设计性强、耐高温、耐疲劳等特性,已被广泛应用于航空、航天、武器、船舶、交通、建筑等领域。FRP 层合板是主要的结构形式,应用范围也最广泛,然而传统的FRP 层合板各向异性严重,垂直于纤维方向的力学性能较低,抗分层能力弱,限制了其优势性能的充分发挥。
随着纳米材料的发展,一些基于纳米填料改性的复合材料增韧技术受到了关注。碳纳米管(carbon nanotube, CNT)是最典型的纳米填料,它可作为基质富集区域的增强材料而分散在基体中。当裂纹扩展至碳纳米管附近时,碳纳米管横亘在裂纹前端,通过桥联作用抑制裂纹扩展(裂纹桥接),裂纹继续扩展将涉及路径偏转或碳纳米管的脱黏、拔出、断裂,引起开裂能的耗散,从而提高FRP 复合材料的断裂韧性。同时,碳纳米管的加入还增强了纤维和基体间的界面强度,改善了FRP 层合板中的应力分布。以碳纳米管(纳米级)、纤维(微米级)、聚合物基体制备的多尺度复合材料,不仅具有抗冲击损伤、抗分层等优异的力学性能,而且还具有吸波、隐身、防雷击等优点,这进一步扩大了FRP 复合材料的应用潜力。
关于CNT 基体改性对CFRP 力学性能影响的研究发现,CNT/CFRP 复合材料的强度、模量、断裂韧性、界面剪切强度和层间剪切强度等都有不同程度的提高。Tarfaoui 等利用ABAQUS 软件的基于Hashin 准则的FRP 本构模型,对CNT/CFRP 层合板的开孔拉伸实验进行了数值模拟,考虑不同含量CNT 对CFRP 的力学性能(模量和强度)的影响,模拟结果与实验载荷-位移曲线吻合较好。而CNT/CFRP 层合板在冲击载荷作用下响应和破坏的数值模拟,目前尚未见相关报道。
本文中,拟对CNT/CFRP 层合板的冲击响应和破坏进行数值模拟。首先,基于文献[7-9]的研究,引入基体增韧因子、残余强度因子,改进损伤耦合方程,建立新的FRP 动态渐进损伤模型,以描述碳纳米管基体改性为FRP 带来的增韧效果;然后,利用所建立的模型并结合黏结层损伤模型,对CNT/CFRP 层合板在低速冲击作用下的响应和破坏进行数值模拟,并与实验数据进行比较;最后,利用建立的模型,进一步研究冲击速度对FRP 层合板冲击响应的影响。
1 FRP 动态渐进损伤模型
由于纳米填料(如碳纳米管)的尺度是纳米级、纤维的尺度是微米级,将这两种增强相建立为一个模型是不现实的。另外,传统的FRP 渐进损伤本构模型描述的复合材料行为偏弹脆性,没有考虑CNT 改性带来的增韧效果。因此,仍将纳米填料改性的纤维增强树脂基复合材料视为宏观上的正交各向异性材料,引入基体增韧因子、残余强度因子,改进损伤耦合方程,建立可描述复合材料韧性行为的新FRP 动态渐进损伤模型。
1.1 损伤准则
纤维增强树脂基复合材料的失效模式原则上可以分为纤维失效和基体失效两种,每种失效又因不同的加载方式而存在不同的模式。基于Yen的损伤准则思路,针对编织纤维增强树脂基复合材料,考虑3 类纤维损伤(面内的纤维拉/剪损伤、面内的纤维压缩损伤、厚度方向的纤维压溃)和2 类基体损伤(面内的基体剪切损伤、厚度方向的基体拉/剪损伤)。这里,给出相关变量和材料常数:损伤因子f,当f≥ 1 时相应模式的损伤开始发生;拉伸强度、、;压缩强度、、;纤维剪切强度、;基体剪切强度S、S、S。其中,下标、、分别代表3 个材料主方向。
(1)面内的纤维拉/剪损伤
纤维方向的拉伸载荷以及横向冲击作用下厚度方向的剪切载荷会使纤维拉直、基体损伤,进而造成纤维断裂。与基体材料相比,纤维的刚度和强度更大,纤维方向上的应力主要通过纤维传递,基体的损伤几乎不会削弱纤维中拉伸应力的传递。因此,面内的拉剪损伤起始由纤维决定,经纱纤维和纬纱纤维的损伤因子分别为:

式中:为库伦摩擦角。厚度方向剪切作用下的基体损伤和厚度方向的压缩应变ɛ相关,遵循Coulomb-Mohr 理论。
需要指出,式(6)~(7)中的与文献[9]中的有不同的意义。在文献[9]中,作为分层修正系数,仅在描述厚度方向基体拉/剪破坏的损伤准则中添加,用于描述FRP 层间弱界面影响,通常大于1。而在本文中,将引入黏结层损伤模型来讨论层间分层情况,只作为基体增韧因子,添加至描述基体损伤的项(模式6~7),用于描述CNT 基体改性对FRP 的增韧效果,通常小于1。
1.2 损伤软化及损伤耦合
纤维增强树脂基复合材料层合板达到上述损伤准则的阈值后,材料的应力和刚度并不迅速下降为零,而有一个逐渐累积退化的过程。通常假设,FRP 层合板的损伤演化由模量的逐渐退化导致失效。在有限元计算中,仅用模量退化描述的损伤演化行为,会产生应变集中从而导致计算结果强烈的网格依赖性。Xin 等引入单元特征尺寸(δ=),采用应力-位移关系取代通常情况下的应力-应变关系来描述材料的损伤演化过程,该方法能在一定程度上解决单元敏感性问题。本文中,损伤演化过程也采用应力-位移关系。
纤维和基体损伤是根据方向区分的,实际上只是某一方向的损伤由纤维或基体主导。例如,纤维方向的拉伸失效,虽由纤维断裂不断累积造成,但基体同样也发生破坏。通常,树脂基体的失效应变比增强纤维的失效应变高很多,因此,在纤维断裂后,载荷会从纤维转移至纤维基体界面,断裂的纤维从基体中拔出也将吸收一部分能量。纳米填料加入FRP 的树脂基体中,为纤维基体界面提供了更有效的载荷传递,界面剪切强度提高,最终,纤维拔出阶段载荷强度提高。本文中,在Xin 等的线性损伤软化的基础上,引入残余强度因子描述断裂纤维从基体中拔出过程的吸能。对纤维的损伤演化采用图1(a)所示的双线性软化形式,其中段为损伤开始前的弹性阶段,段为纤维逐渐断裂的过程,段则为断裂纤维从基体中拔出的过程。另外,由于基体损伤主导方向的强度较低,这部分损伤通常开始早、发展快,为避免基体损伤发展过快而主导最终的破坏,对基体的损伤演化采用如图1(b)所示的演化形式,相当于=1。如=0,则退化为原线性软化形式。
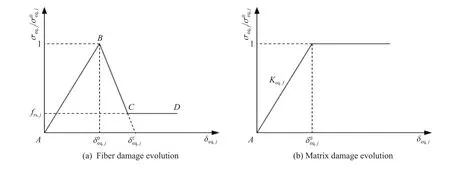
图1 损伤演化示意图Fig. 1 Schematic diagrams of damage evolution

不同损伤模式的等效位移和等效应力的计算方法见表1。

表1 等效位移和等效应力Table 1 Equivalent displacement and equivalent stress
FRP 复合材料不同模式的损伤演化不是完全独立的,他们存在相互作用,因此引入损伤变量ω,表示受到不同破坏模式ϕ协同作用后模量的缩减程度。在MAT162、FRP 本构模型中,不同模式下的损伤以加和的形式耦合(ω=qϕ),这样损伤耦合形式预测的损伤量偏高,基体损伤主导了最后的破坏,这是不够准确的。因此,本文中提出了乘积式耦合:

其实,原加和形式的损伤耦合就相当于提取了式(11)的一阶近似,在损伤为小量时,两者是等价的,而对于损伤很容易达到1 情况(如冲击、侵彻等),采用乘积形式的损伤耦合形式更合理。

1.3 失效准则
考虑FRP 单层板的各向异性,与MAT162 类似,以下3 种失效准则用于有限元模拟中的单元删除:(1)基于最大应变准则的纤维拉伸失效,当ɛ≥ɛ或ɛ≥ɛ时,单元删除;(2)基于体应变的拉伸和压缩失效,当ɛ≥或ɛ≤时,单元删除;(3)基于等效应变的畸变单元删除,当≥时,单元删除。
1.4 应变率效应

另需指出的是,本文中模型适用于一般的FRP 层合板,为了本构模型的完整性,考虑了应变率效应。但对下面数值模拟验证所采用的CFRP 层合板,由文献[7]得知CFRP 应变率效应不敏感,因此在数值模拟中,取动态增强因子=1,即经验参数=1。
2 黏结层损伤模型
蒋振等提出了考虑应变率效应的黏结层损伤模型,该模型基于B-K 失效准则,引入与FRP 本构模型中相同形式的动态增强因子,考虑牵引力-位移关系中刚度与强度的应变率效应,混合模式下的分层损伤通过损伤变量描述。黏结层损伤模型的具体介绍见文献[10]。
3 有限元模型与材料参数
Soliman 等对4 种MWCNTs(multi walled carbon nanotubes)含量的碳纳米管改性编织碳纤维增强树脂基复合材料进行了5 种能量下的落锤冲击实验。本文中,根据实验中的描述,建立了有限元模型,如图2 所示。落锤系统简化为直径12.7 mm、质量14.93 kg 的球头弹;靶板尺寸为50 mm×50 mm×2.7 mm,单层板厚度为0.27 mm,共10 层,层与层之间通过偏置方法插入了零厚度的Cohesive 单元,FRP 单元与Cohesive单元是共节点的。在满足求解精度的条件下,为了提高计算效率,对靶板进行如下形式的网格划分:冲击影响区域(约2 倍弹径)30 mm×30 mm 范围内单元较密(面内尺寸为0.5 mm×0.5 mm)、外围较疏(面内尺寸为1 mm×1 mm),中间采用蝴蝶型网格过渡。弹体和FRP 单层板用C3D8R 单元创建,黏结层用COH3D8 单元创建。靶板四周施加固定约束,弹体设置为刚体,弹体与靶板间采用通用接触,摩擦因数设为0.2。对弹体施加的速度分别为1.42、1.8、2.0、2.85 和4.0 m/s,用以模拟能量分别为15、24、30、60 和120 J 的落锤冲击实验。
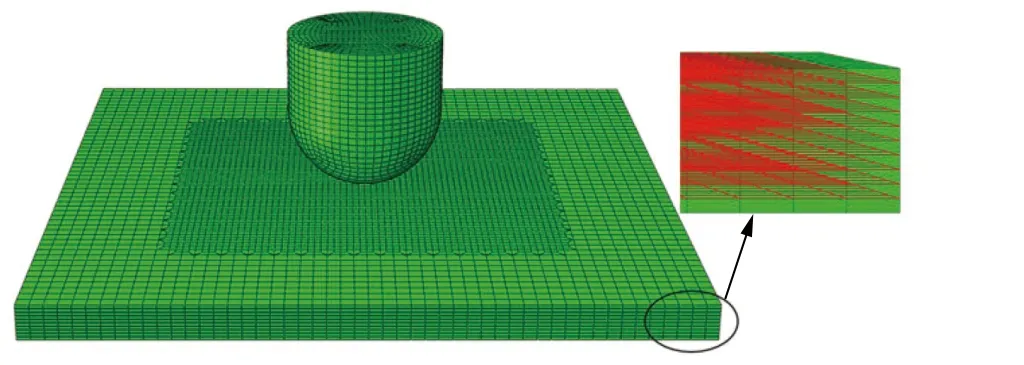
图2 冲击载荷下 CFRP 层合板的有限元模型Fig. 2 Finite element model for CFRP laminates under impact loading
本文中新的FRP 本构模型及文献[10]中的黏结层损伤模型,通过用户材料子程序(VUMAT)编程实现并嵌入到有限元软件ABAQUS 中,用于碳纳米管改性碳纤维增强复合材料冲击实验的模拟。下面简单介绍模型中相关材料参数的确定。
表2 为CFRP 单层板的材料参数,这些参数来源于文献[12-14],暂未考虑碳纳米管改性对CFRP 层内强度和模量的影响,因而在算例中,这部分参数是相同的。表3 为反映碳纳米管改性对CFRP 影响的材料参数,包括基体增韧因子、残余强度因子、失效参数ɛ、ɛ、、、,这些参数通过试算确定,不考虑经纱和纬纱纤维的不同,认为ɛ和ɛ相等。

表2 CFRP 单层板的材料参数Table 2 Parameters for CFRP laminate
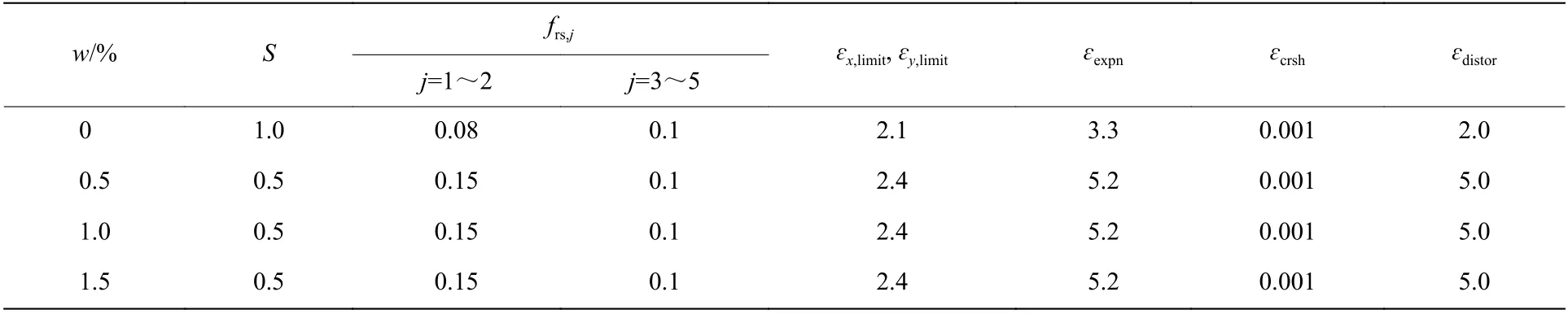
表3 CNT/CFRP 材料参数Table 3 Parameters for CNT/CFRP laminates
在分析大量实验数据的基础上,给出了CNT/FRP 层间剪切强度随CNT 含量变化的规律,如图3 所示。可以看出,当CNT 含量不超过2.0%时,CNT/FRP 的层间剪切强度与CNT 的质量分数成近似线性关系,可以用经验公式表达:

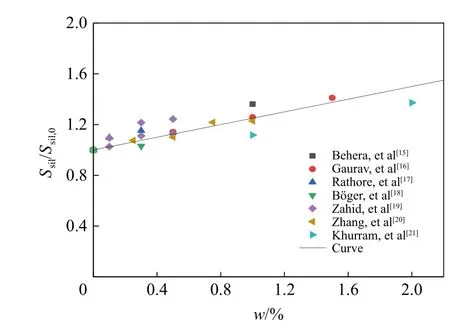
图3 CNT 含量对CNT/FRP 层间剪切强度的影响Fig. 3 Effect of CNT content on the intelaminar shear strength

图4 不同CNT 含量黏结层模型的牵引力-位移关系Fig. 4 The traction-separation law in the cohesive element model with different CNT contents

表4 黏结层单元参数Table 4 Parameters for cohesive elements
4 结果与讨论
图5 为数值模拟得到的载荷-位移曲线与实验的比较,图中红线为数值模拟结果,黑线为实验曲线。实验结果显示: MWCNTs 含量0.5%、1.0%和1.5%的CFRP 层合板在能量15、24、60 和120 J 冲击下的峰值载荷是相近的,均约为2.8 kN,只有能量30 J 冲击下MWCNTs 含量1.0%和1.5%的CFRP 层合板峰值载荷有所差别(3.5 kN),Soliman 等未给出合理解释。由图可以看出,数值模拟预测的峰值载荷、平台长度都与实验结果吻合较好。总体来看,新建立的FRP 本构模型能够较准确地描述碳纳米管基体改性对CFRP 的增韧效果,这种增韧效果主要体现为冲击响应过程中载荷在达到峰值后维持一段时间不变即在载荷-位移曲线中呈现一段平台,本文中提出的模型能较好地描述这个现象。另外,本文中还未考虑碳纳米管改性对CFRP 层内强度和模量的影响,若考虑则会得到与实验更吻合的模拟结果。
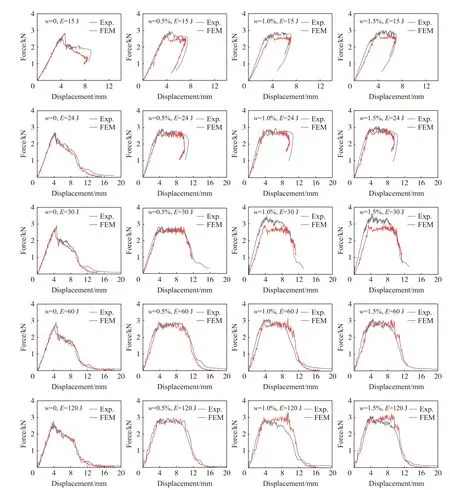
图5 数值模拟的载荷-位移曲线与实验[11]的比较Fig. 5 Comparison of the force-displacement curves between numerical simulation and experiment[11]
图6 为数值模拟的破坏形貌的正面图和侧面图与实验结果的比较。由图可以看出,模拟结果与实验相同,靶板形成鼓包,背面呈现十字形破坏。

图6 数值模拟的破坏形貌与实验[11]的比较Fig. 6 Comparison of the damage morphologies between numerical simulation and experiment[11]
图7 为数值模拟的MWCNTs 含量0.5%的CFRP 层合板在能量120 J 冲击下的破坏历程。由图可以看出,破坏的各阶段与载荷-位移曲线的特征相对应。在冲击过程中,先是冲击面的压缩损伤(见图7(a)),接着是冲击背面开始的自下而上发展的拉伸损伤(见图7(b)),拉伸损伤集中在各层的十字形区域;在压缩损伤与拉伸损伤在中间层汇集前,接触力不断增大,当两种损伤在中间层汇集时,接触力达到峰值(见图7(c)),对应载荷-位移曲线平台起点;而后损伤继续在面内扩展,此过程接触力维持几乎恒定(见图7(d)),对应载荷-位移曲线的平台段;当冲击背面开始拉伸破坏(见图7(e))删除单元时,对应载荷-位移曲线平台终点;随着自下而上的拉伸破坏,单元相继被删除,接触力逐渐减小,直至完全穿透(见图7(f)~(h))。

图7 数值模拟的破坏历程Fig. 7 Damage histories obtained by numerical simulations
图8~9 分别为数值模拟的能量15 和120 J 冲击下不同含量MWCNTs 增韧CFRP 层合板的层间损伤云图。由图8 可以看出,当冲击能量较低不足以穿透CFRP 层合板时,随着MWCNTs 含量的增加,层间界面的分层损伤面积逐渐减小。而当冲击能量较高CFRP 层合板被穿透时,分层将承担一部分吸能。由图9 可以看出:相较于CFRP 层合板,MWCNTs/CFRP 层合板分层面积增大,因此吸能增多;但是,随着MWCNTs 含量增加,分层面积逐渐减小,最大分层面积出现在中性层及其附近的层间界面5-6(CFRP 层合板总共有10 层,界面5-6 刚好就对应中性截面)。经分析,当弹体穿透到中性层时,中性层以下FRP 因面内拉伸损伤而难以承受面外压缩载荷,弹体继续前进将造成中性层附近的层间界面撕裂,直到层合板的未打穿部分因为面内拉伸破坏,最终被穿透。

图8 冲击能量为15 J 时不同MWCNTs 含量CFRP 层合板的分层形貌Fig. 8 Delaminations of CFRP laminatses with different MWCNTs content under the impact energy of 15 J

图9 冲击能量为120 J 时不同MWCNTs 含量CFRP 层合板的分层形貌Fig. 9 Delaminations of CFRP laminates with different MWCNTs content under the impact energy of 120 J
为进一步探讨冲击速度对CNT/CFRP 冲击响应的影响,在CNT 含量0.5%、冲击能量120 J的算例中,保持其他参数不变,只改变弹体密度和冲击速度,实现相同冲击能量下不同冲击速度的加载。图10 为相同冲击能量不同冲击速度下的载荷-位移曲线,可以看出,随着冲击速度的提高,载荷-位移曲线的首次峰值载荷提高,平台后端上翘。图11 为不同冲击速度下FRP 层合板中间三层的最终层内损伤云图,为辨别拉伸和压缩破坏,不显示变形。中心圆形的损伤由压缩造成,十字形损伤则由拉伸引起。可以看出,随着冲击速度的增大,CFRP6 中心压缩损伤区域逐渐减小,穿透该层涉及更多的拉伸撕裂。因此,冲击速度会影响FRP 层合板压缩和拉伸破坏的比例,相同冲击能量下,更大的冲击速度会造成更多的拉伸破坏。
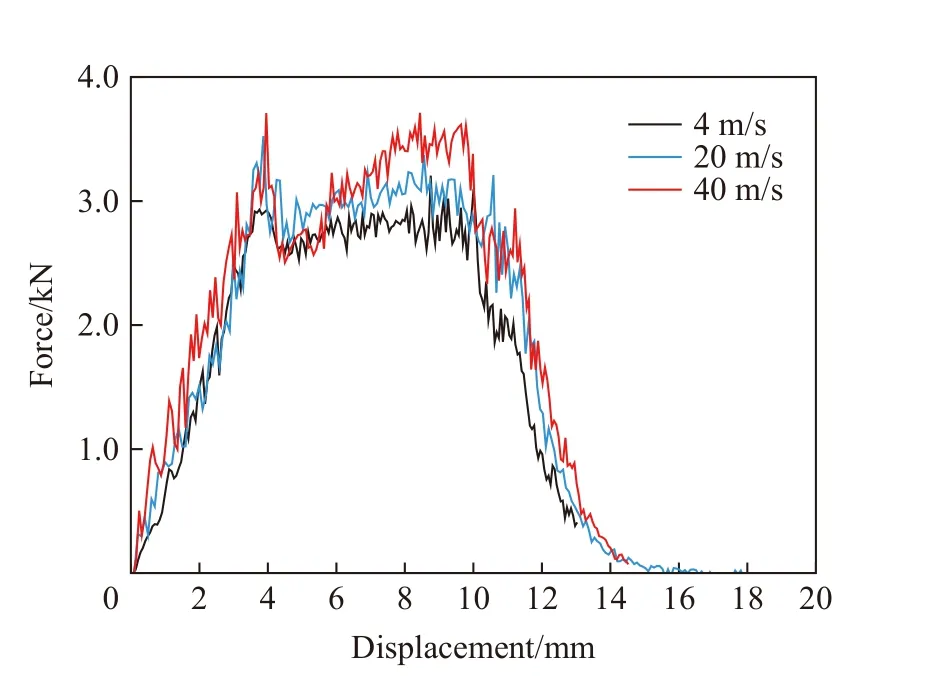
图10 冲击能量为120 J 时不同冲击速度对CNT/CFRP 冲击载荷-位移曲线的影响Fig. 10 Effect of impact velocity on the impact load-displacement curve for CNT/CFRP under the impact energy of 120 J
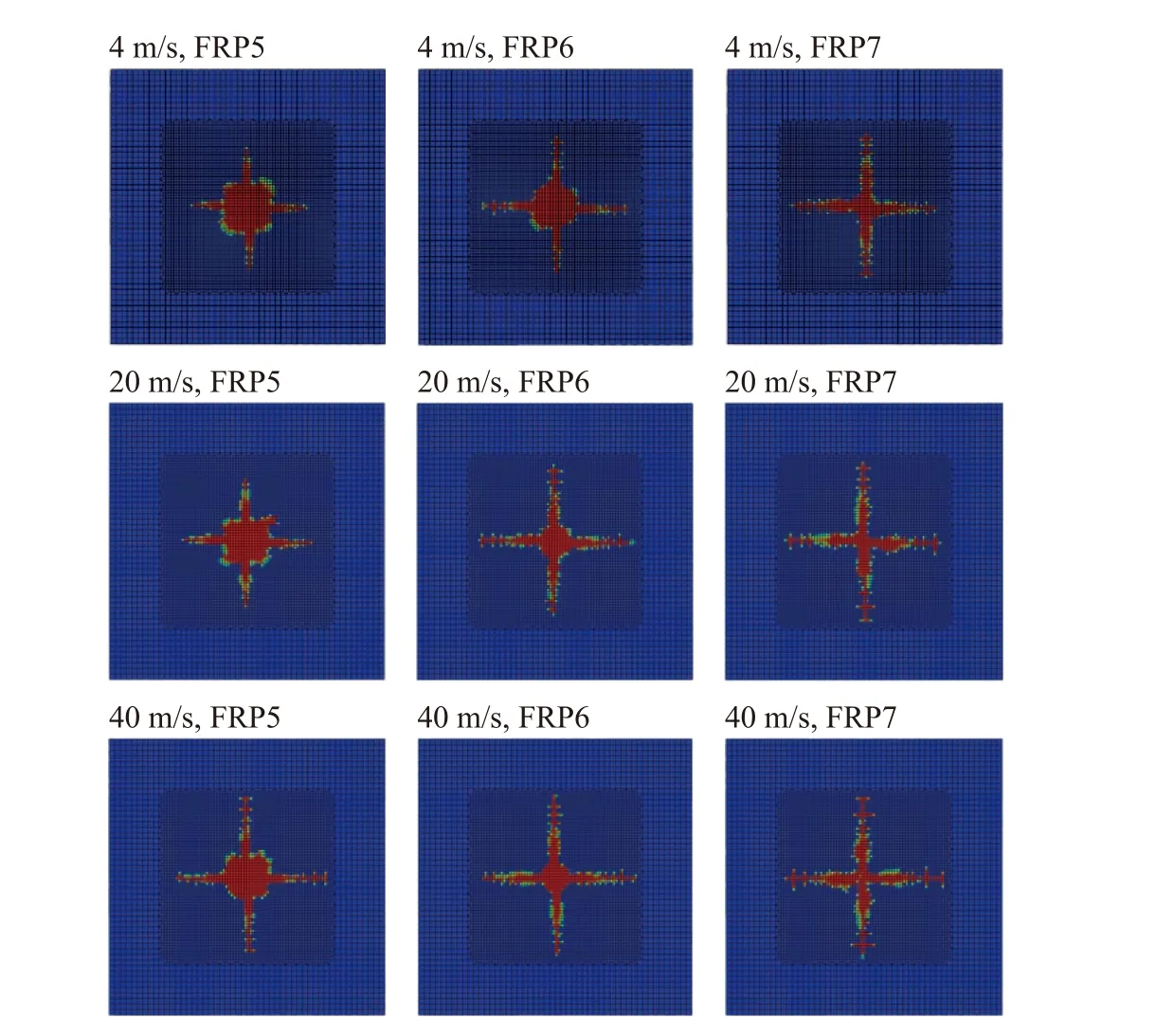
图11 冲击能量为120 J 时下不同冲击速度对CNT/CFRP 损伤的影响Fig. 11 Effect of impact velocity on the damage of CNT/CFRP under the impact energy of 120 J
5 结 论
对碳纳米管/碳纤维增强复合材料(CNT/CFRP)层合板低速冲击下的响应和破坏进行了数值模拟。基于先前的研究工作,引入基体增韧因子、残余强度因子并改进损伤耦合方程,建立了新的FRP 动态渐进损伤模型,该模型能够描述纳米填料掺入纤维增强复合材料基体后的增韧效果。将模拟结果与文献[11]中的相关实验结果进行了比较,并讨论了冲击速度的影响。结果表明:新建立的FRP 本构模型能够预测CNT/CFRP 层合板在低速冲击载荷作用下的响应、破坏过程和分层形貌,模拟得到的载荷-位移曲线和破坏形貌与实验较好吻合;冲击速度会影响CNT/CFRP 层合板拉伸和压缩破坏的比例,相同的冲击能量下,更大的冲击速度会造成更多的拉伸破坏。
