飞机机翼油箱晃振仿真与全尺寸试验验证

2022-04-09王东林陈良斌

工程力学 2022年4期

王东林，安丽，胡豪，马松，李明，陈良斌

(1. 中国民用航空沈阳航空器适航审定中心，沈阳 110043；2. 大连理工大学工业装备结构分析国家重点实验室，大连 116024；3. 江西洪都航空工业集团有限责任公司，南昌 330024；4. 中航通飞研究院有限公司，珠海 519040)

飞机飞行过程中，机翼油箱液体表面受扰动或激励产生绕飞机纵向的晃动，因气动紊流和发动机转子工作发生沿挂点的振动[1−2]。晃动与振动常同时发生，形成晃振，使机翼油箱出现连接件松动、渗油、局部磨损或断裂等现象，造成经济损失和人员伤亡。出于飞行安全考虑，飞机适航审定需要合理评估飞行过程中机翼油箱的晃振响应[3]。

现行飞机适航审定多基于全尺寸机翼油箱晃振物理实验，提出了诸多试验方案和试验标准等[2,4−5]。王轩等[1]给出了飞机机翼油箱结构晃振试验台设计，满足晃振动力学分析与控制的要求。叶休乃[4]综述了飞机油箱的晃动或晃振试验，建议制订适合我国的飞机油箱晃动及晃振试验标准。翟冰冰等[5]结合适航要求，提出了飞机滑油箱晃振试验各参数的确定方法。Kim等[6]研究了急转和加速运动下的油箱晃振对油箱内部件和油箱蒙皮的影响，给出油箱适航实验方案和结果。Rajamani等[7]和Golla等[8]基于物理实验研究了匀加速和周期激励下的液舱晃荡，分别给出了自由液面和晃动噪音的变化趋势。Diego等[9]实验确定了激励频率对储箱壁面压力的影响，认为低频激励下，晃动行为控制壁面应力的发展。全尺寸试验虽能准确反映油箱晃振行为，但存在代价高、周期长等问题，不利于飞机适航审定和概念设计。

数值仿真基于力学理论模拟复杂结构变形和失效行为，具有经济快速和复用性强等特点，潜在应用于机翼油箱晃振适航审定[10−11]。Elena等[12]研究圆柱形储液箱在水平和竖直激励下的振动，并给出合理的隔板设计。Lin和Wang[13]分析单向水平激励下的圆形RC液箱的液面晃动规律，确定了液箱的最大晃动波幅。秦念等[14]采用半解析法研究了水平激励下不同截面柱形储液罐内液体晃动的固有频率及晃动响应特点。尹立中等[15]研究了规则矩形储液箱在受俯仰激励情况下流固耦合系统动力学特征。李威锋[16]根据航标规定工况建立油箱流固耦合模型，研究了载液量、晃动幅值以及晃动频率对结构危险位置应力的影响。吴早凤等[17]得到了整体油箱液面在晃动过程中可近似为准静态现象以及油箱结构应力响应与激励载荷时程趋势一致等结论，为油箱结构设计及试验提供了参考。刘文夫等[18]、管官等[19]、唐亮等[20]和袁雄飞[21]分别针对独立液舱、C型液货舱、LNG液舱和机翼油箱等晃荡开展数值分析，有效指导工程实际。方治华等[22]开展燃油箱系统流固耦合振动分析，指出载液量是影响燃油箱系统振动频率的主要因素。张鹏飞[23]开展燃油箱振动分析，基于应力与变形考量给出结构改进方案。宝鑫等[24]开展储液结构动力学响应分析，指出频率和载液量影响动力学反应峰值。徐文雪和吕振华[25]针对储液减振器开展三维流固耦合数值分析，并考虑了固体结构改变的影响。江勇等[26]和许贺等[27]也开展了储气/液结构的流固耦合分析，为相应结构设计和工艺优化提供技术支持。已有数值仿真较好研究了油箱晃振行为，但多集中于具有简单规则几何结构的油箱开展趋势分析，未能反映真实非规则油箱结构晃振响应，且较少与全尺寸试验比较验证仿真的有效性。

本文以某整体机翼油箱组为研究对象，开展非规则油箱晃振分析，考虑晃/振动频率、幅值和载液量等因素，基于流固耦合和复合材料分析，预测油箱应变和评估结构安全。开展全尺寸机翼油箱晃振试验，验证机翼油箱晃振数值仿真的有效性。基于数值仿真和全尺寸试验结果，给出机翼油箱应变随油箱载液量、晃动幅值与频率、振动幅值与频率变化的响应规律，揭示机翼油箱晃振失效机理，为飞机适航审定提供有效指导性意见。

1 机翼油箱晃振数值仿真

本文以如图1所示的在机翼上间隔分布的6个非规则形状油箱为研究对象，机翼蒙皮采用碳纤维预浸布和泡沫组成的夹芯铺层结构。将三维CATIA模型在Hypermesh中完成固体域的简化、抽壳和网格剖分，然后在ANSYS Workbench中生成流体域网格。参考《正常类、实用类、特技类和通勤类飞机适航审定规定》，施加0.8 mm振幅的振动载荷和以每分钟20个整循环的速率绕与机身轴线平行的轴沿水平面上、下各15度的晃动载荷。基于数值仿真结果分析载液量、晃/振动频率和幅值对油箱壁面应变水平和失效逆储备因子的影响。

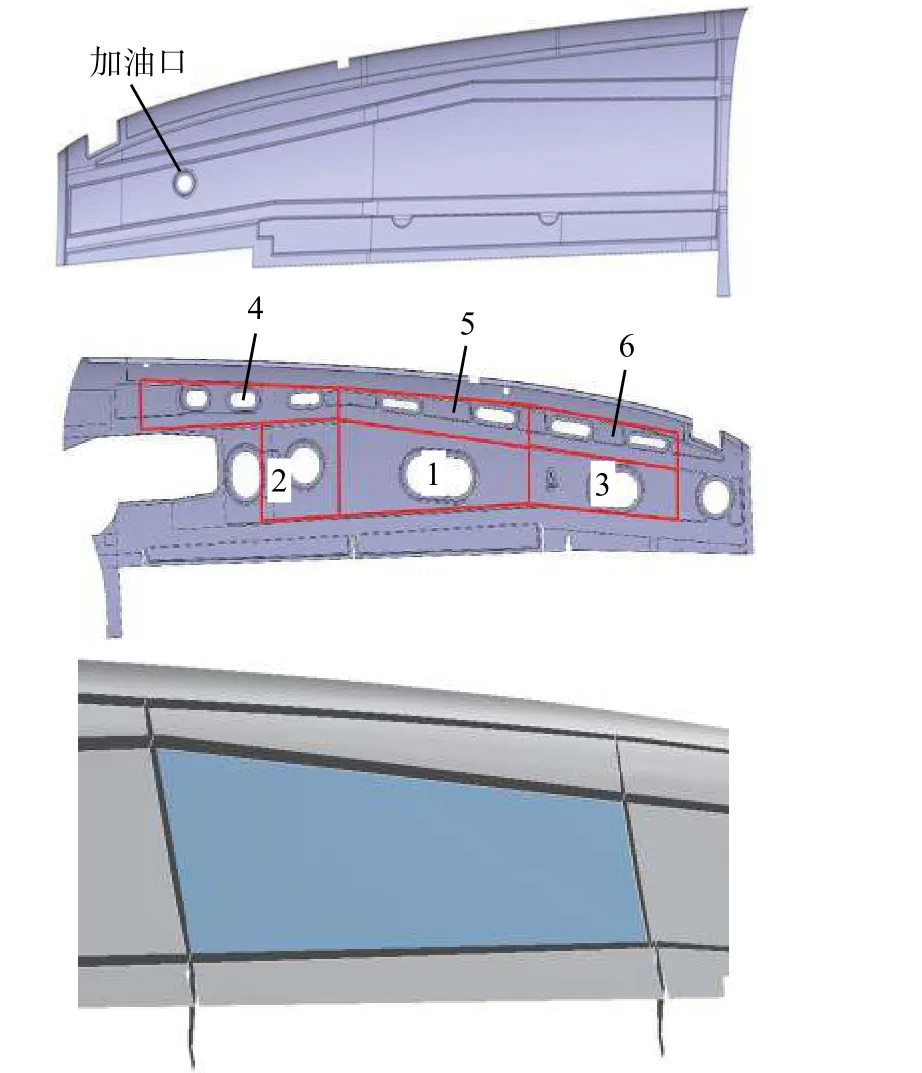
图1 非规则形状机翼和重点关注油箱区域有限元模型示意图Fig.1 Schematic illustration of irregular-shaped wing and finite element model of key fuel tank

1.1 晃动数值分析

本文不考虑气体可压缩性，并假设液体为不可压缩粘性流体，空气与液体间存在自由界面，晃动过程中空气与液体体积分数守恒；不考虑结构大变形引起的流体域变化，仅考虑单向流固耦合开展瞬态分析。使用流体体积法(Volume of Fluid, VOF)跟踪气/液自由表面演变。粘性流体与油箱壁面间采用无滑移边界条件。

机翼油箱内液体晃动的控制方程包括雷诺时均Navier-Stokes方程(RANS方程)、湍流模型方程和体积分数方程，RANS方程中的质量守恒方程为：

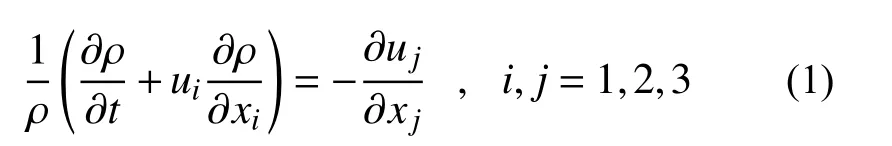
式中：ρ 为密度；ui(i=1,2,3) 为x、y、z三个方向上的时均速度。

RANS方程中的动量方程为：

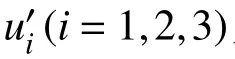
表征自由液面的VOF方程为：

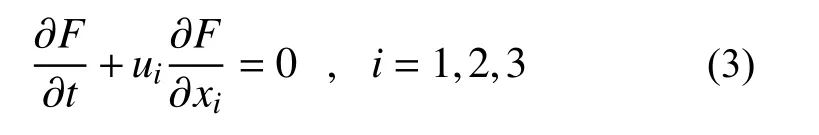
利用商用软件ANSYS Workbench，开展液体晃动分析得到液体对油箱壁面的压力，对机翼整体进行瞬态分析，得到晃动过程中机翼油箱壁面的变形和应变信息。流固耦合交界面使用SIMPLE(Semi-Implicit Method for Pressure-Linked Eqaution)算法保证收敛速度。

晃动数值分析需要对流体域和固体域进行离散网格划分。使用四边形壳单元描述机翼油箱固体域，使用六面体网格描述燃油流体域。固体变形分析快速收敛，时间成本低。流体分析在数值模拟过程中占主导地位，其计算精度和效率取决于流体域网格量和时间步长。因此，有必要找到满足计算精度要求的流体域最小网格量和最大时间步长，提高计算效率。本文分别考虑不同密度流体域网格量和时间步长，以高密度网格量和小时间步长计算结果为参照系，以流体域左/右/底面在液体晃荡过程中感受的压力合力和最大压力为指标，选取各指标计算误差均小于3%的流体域网格量和时间步长开展流固耦合分析。

1.2 振动数值分析

将液体作为附加质量作用于对应油箱下蒙皮上，使用模态叠加法开展机翼油箱振动分析，在模态解的基础上解耦求解动力学方程，基于模态坐标响应开展线性变换确定机翼油箱在物理坐标下的结构振动响应。

不考虑系统阻尼影响的多自由度系统的动力学方程为：

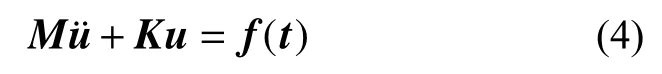
式中：M为质量阵；K为刚度阵；u为位移向量；f(t)为激振力。式(4)对应的特征频率方程为：

式中：ω为固有频率；φr为特征向量。基于模态结果可线性叠加特征向量确定模态叠加法假设位移矢量u：

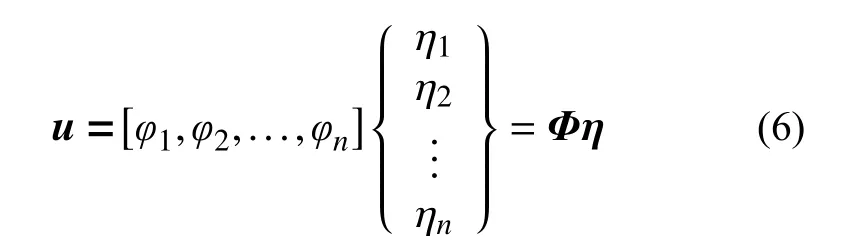
式中： Φ为模态振型矩阵；η为模态坐标。特征向量正交性使得式(5)可转换至模态坐标系下，从而实现动力学方程的解耦，通过求解模态坐标得到位移矢量。模态坐标系下，动力学方程为：

式中：模态质量阵M∗=ΦTMΦ，模态刚度阵K∗=ΦTKΦ ，激振力f∗(t)=ΦTf(t)。

1.3 晃振数值分析

晃振激励下机翼油箱响应复杂，既包含了相对独立的低频晃动成分和高频振动成分，也包含了晃动和振动耦合成分。晃振耦合增加了数值分析的难度和计算代价。晃动不引起油箱壁面较大变形，振动不引起自由液面剧烈变化，相对于振动，时间周期长的晃动可视为准静态过程。这些特性使得振动与晃动可解耦处理，从而将晃振视为晃动和振动响应的叠加[16−17]，大大简化了晃振数值仿真。

为了验证晃振解耦的正确性，对晃振实验进行测点频幅分析。以工况6为例，如图2所示可知油箱晃振响应集中在晃动激励的倍频(0.64 Hz)和振动激励的倍频(29.85 Hz和59.68 Hz)上，而晃动和振动耦合响应对油箱壁面最大主应变的贡献较小，可忽略不计。因此，本文将晃振解耦，视为晃动与振动响应的叠加的做法是合理的。

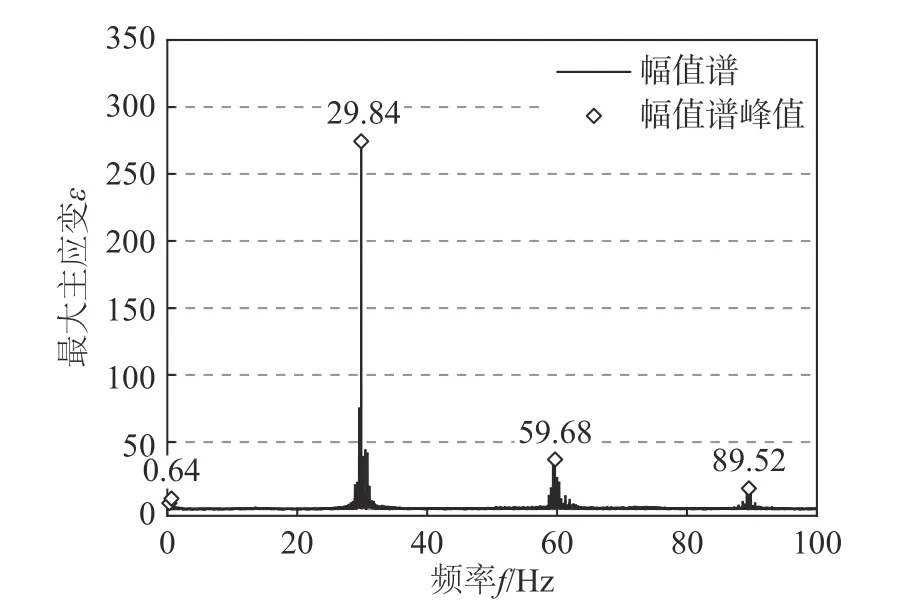
图2 晃振响应频谱分析Fig.2 Frequency-response analysis for a sloshing and vibration case

1.4 油箱复合材料壁面失效分析

机翼油箱的复合材料壁面破坏是损伤累积并最终扩展至结构整体破坏的过程。目前复合材料层合板破坏准则，主要有最大应变准则、最大应力准则、Tsai-Hill准则、Tsai-Wu准则等。本文使用最大应变准则评估油箱壁面的失效情况。

最大应变准则认为当某区域主方向的正应变或剪应变超过某一阈值时就发生失效，其判别式为：

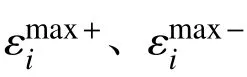
2 机翼油箱全尺寸晃振试验

如图3所示，选取某机型右机翼整体油箱和左机翼前后梁对称面至左机翼1000 mm的梁段作为试验件，试验件结构重量150 kg，并对所有油箱进行隔段密封处理。试验件通过夹具紧固于振动台台面上，保证了机翼燃油箱与机身的连接刚度。晃动激励由作动筒与橡皮绳拉动夹具和机翼施加，振动由振动台通过转轴连接机翼施加。试验所需的载荷施加、信号处理、数据采集等设备如表1所示。晃振试验工况如表2所示，其中晃幅±10°是指机翼绕水平转轴上下各10°，振幅0.8指全幅0.8 mm，晃频20次/min指以每分钟20个整循环的速率绕与机身轴线平行的轴摇晃油箱，载液量1/3或2/3是指油量占其油箱容积比，共振频率(R)由试验件加水后扫频确定。每个工况试验时长为响应稳定后持续10 min。测定振动位移和主应变的采样频率均为500 Hz。

图3 全尺寸机翼油箱晃振试验示意图Fig.3 Illustration of sloshing and vibration qualification test for wing fuel tank

表1 试验设备Table 1 Experimental instruments

表2 机翼油箱晃振试验工况Table 2 Sloshing and vibration cases for wing fuel tank

机翼油箱晃振试验中，振动位移测点布置在刚度较大且有利于反映机翼整体振动的位置，如上蒙皮外表面梁肋交界处等。应变测点分布如图4所示，基于数值仿真结果选取时程响应中应变较大且几何/应变梯度变化不明显的区域，考虑一定间隔半径确定应变测点位置。应变测点数据后处理包括不合理数据点的剔除、最小二乘法进行趋势项的消除、数据滤波和基于应变分量给出最大主应变。

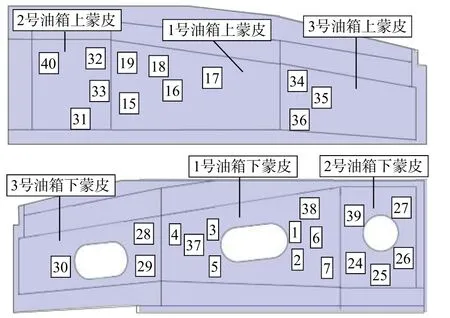
图4 油箱上下蒙皮应变测点分布示意图Fig.4 Illustration of strain gauge distribution on the top and bottom skins

3 结果与讨论

本文研究晃动、振动和晃振等工况下机翼油箱应变幅值随载液量、晃/振动幅值和频率等变化的时程响应，考量数值仿真在适航审定中替代全尺寸试验的可行性，预测机翼油箱危险区域，揭示机翼油箱失效机理，为适航审定提供指导性意见。为降低问题复杂度，本文仅考虑中间1号油箱充液，但本文工作可方便拓展至各油箱非均匀载液工况。

3.1 晃动分析

以表2所示的晃动工况1为例，提取1号主油箱下蒙皮贴片点(4号、5号和37号)对应的最大主应变时程曲线如图5所示。数值仿真(实线)与全尺寸试验(散点)得到的最大主应变时程曲线的幅值与周期一致，均出现了主峰与次峰，较好反映了机翼油箱的晃动时程响应。表2各晃动工况下的应变测点的最大主应变峰值变化趋势如图6所示，仿真(实线)与实验(散点)主应变峰值结果相吻合，以工况1为例，最大误差仅为8.5 µε，远远小于重点关注的载液油箱附近测点数据(3号测点为118 µε)。由图5的主应变时程曲线和图6的主应变峰值变化趋势可知，数值仿真替代全尺寸试验用于适航审定对于晃动工况是可行的。

图5 晃动工况1油箱部分贴片点最大主应变时程曲线Fig.5 Time-history curves of maximum principal strains for strain gauges for the sloshing case 1

数值仿真与全尺寸试验存在的晃动分析数值误差对机翼油箱壁面失效影响较小。如图5所示的晃动时程响应中，数值与实验存在波形误差，由数值仿真中将真实加载简化为光滑正弦激励导致。但油箱壁面失效受应变峰值决定，此波形误差可忽略不计。如图6所示的主应变峰值误差多出现在空载油箱(2号和3号油箱)贴片点，在实验扰动下产生较大的数值噪音。但此处应变幅值较低，油箱壁面失效分析时存在较大的安全裕度，误差可忽略不计。

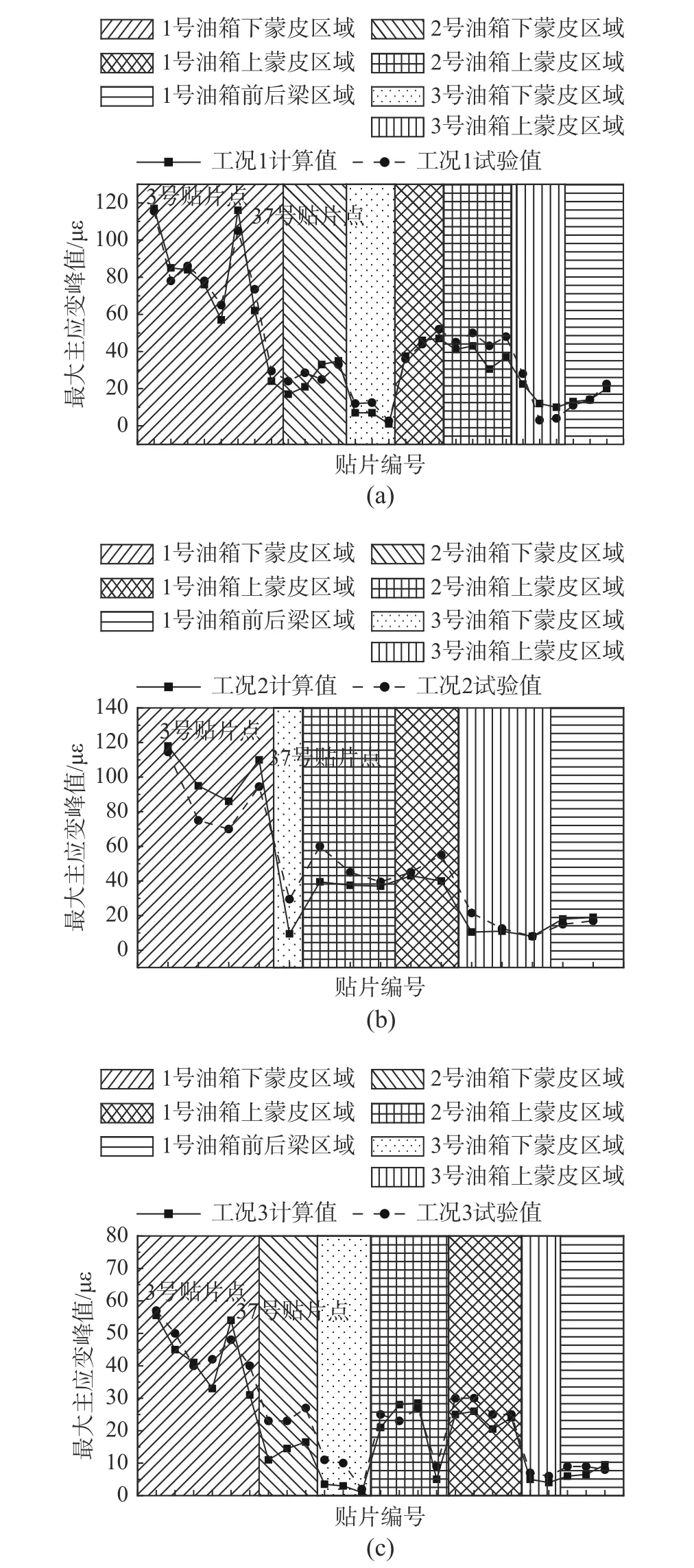
图6 晃动工况机翼油箱应变测点最大主应变峰值分布Fig.6 Peak values of maximum principal strains in wing fuel tanks for sloshing cases

决定机翼油箱失效的主应变峰值受晃动频率、载液量等因素影响。如图6所示，对比不同晃动工况可知，增加晃动频率和减少载液量导致晃动加剧，整个载液部分对下蒙皮的压力降低，但上蒙皮还未呈现明显的晃动液体拍打效果。因此，随着晃动频率的增加和载液量的减少，占主导的载液油箱下蒙皮应变呈降低趋势，但上蒙皮受影响较小。同时，主应变峰值的最大值均发生于主油箱下蒙皮近翼梢侧(3号和37号测点)，几乎不受晃动频率和载液量影响。需要说明的是，如图6所示，从工况1到工况2，晃动频率增加，主应变峰值最大值对应的3号和37号测点应变数值均有下降，而3号和37号之间测点应变数值均有不同程度上升，说明晃动频率增加使得结构整体变形均匀，对机翼的破坏性减小。

3.2 振动分析

振动试验扫频与数值仿真结果如表3所示。1/3载液量时，试验如图3所示，自转轴向右延伸部分及安装夹具会造成质量分布扰动，导致数值结果略高于试验数据。但需要指出的是，此影响随着载液量的增加而不断削弱。当载液量为2/3时，数值仿真与全尺寸试验给出吻合的结果，验证了数值仿真代替全尺寸试验描述机翼油箱振动行为的可行性。

表3 不同载液量模态分析与试验结果对比Table 3 Comparison between modal analysis results and experimental solutions for different fuel loads

机翼油箱的共振频率和受迫振动响应受油箱载液量影响。如表3所示，随着载液量的增加，整体质量增加，造成基频降低。如图7所示，增加载液量，结构重心向翼梢侧移动，共振频率激励下的受迫振动响应越大，从而工况4 (2/3载液量)的主应变峰值远大于工况5 (1/3载液量)的主应变峰值。与图6所示的晃动响应不同，图7结果表明，振动工况下主应变峰值的最大值均发生于1号载液油箱下蒙皮近翼根侧(6号和38号贴片点)，且振动工况下的主应变峰值比晃动工况增加了一个数量级，可知振动引发的应变峰值在晃振分析中应占据主导地位。此外，如图7所示，数值仿真与全尺寸试验给出一致的不同区域最大主应变峰值，说明数值仿真能够准确地描述结构振型与预测受迫振动最危险位置，将数值仿真应用于快速适航审定可行性强。

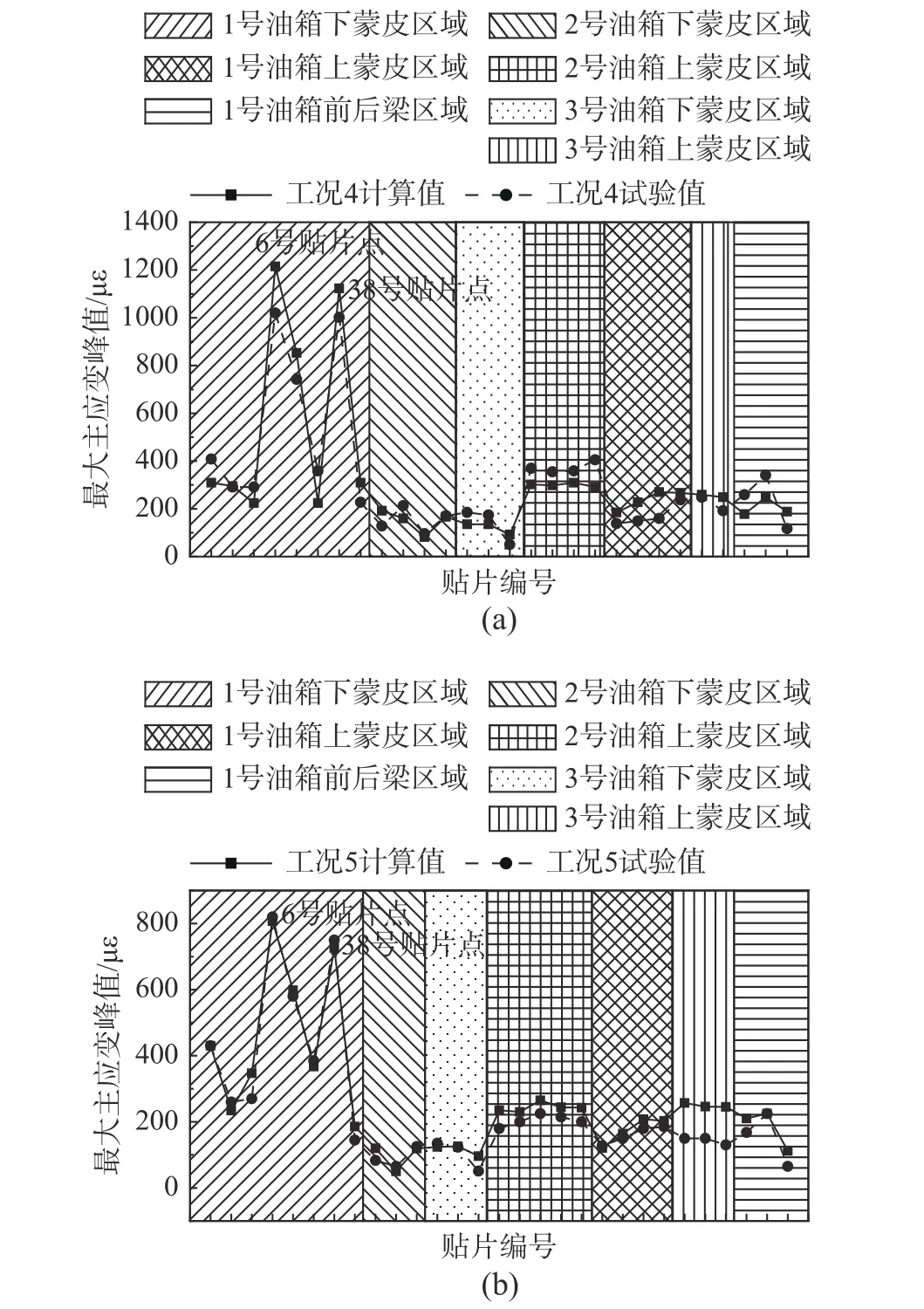
图7 振动工况机翼油箱贴片最大主应变峰值分布Fig.7 Peak values of maximum principal strains in wing fuel tanks for vibration cases

3.3 晃振分析

机翼油箱晃振分析结果如图8所示，数值仿真(实线)与全尺寸试验(散点)给出一致的主应变峰值幅值和趋势，不但说明将晃动与振动解耦可以经济有效地描述机翼油箱晃振行为，还证明数值仿真替代全尺寸试验预测晃振响应的可行性。

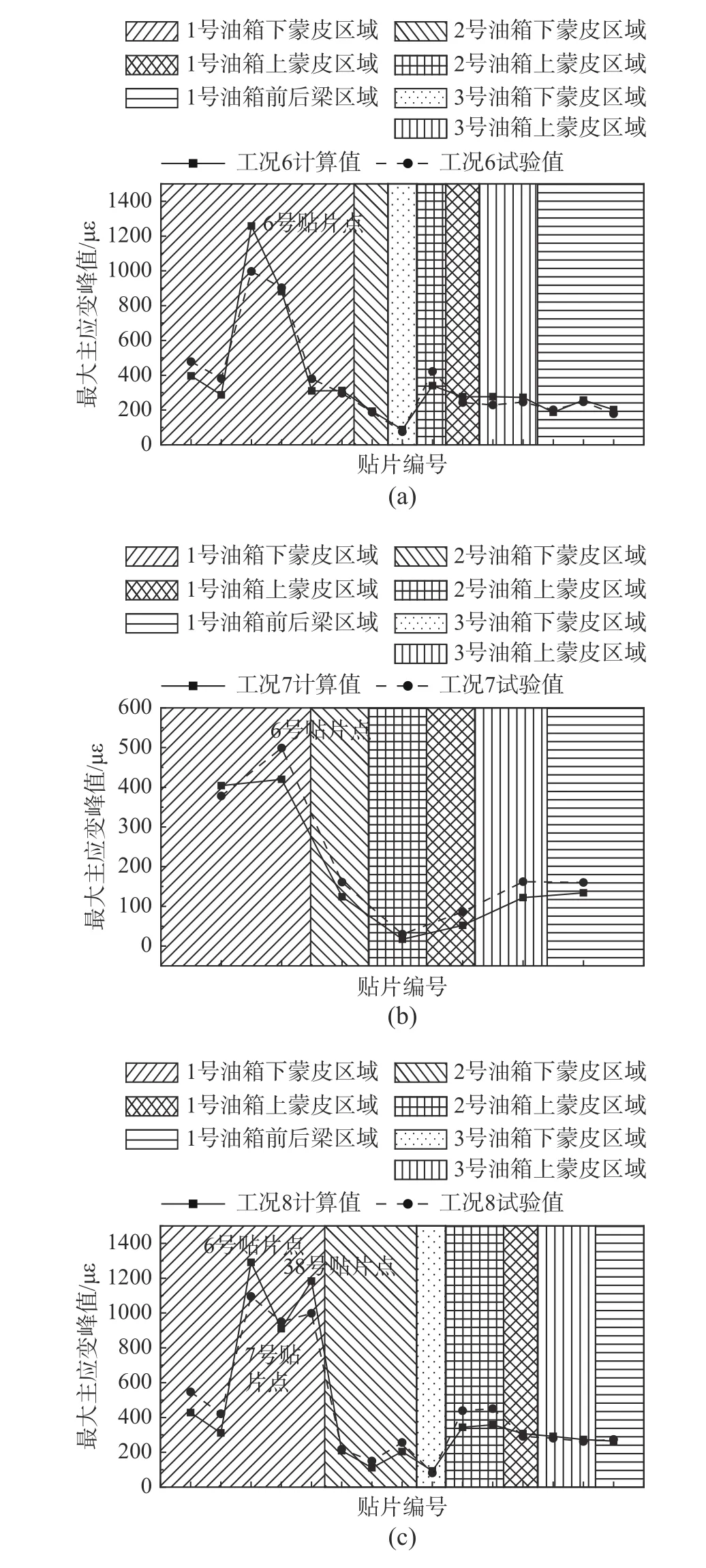
图8 机翼油箱贴片点最大主应变峰值分布Fig.8 Peak values of maximum principal strains in wing fuel tanks for sloshing and vibration cases

决定机翼油箱失效的主应变峰值受晃/振动频率和幅值、载液量等因素影响。分析晃振工况6～工况9可知，当激励频率远离共振点10 Hz时，油箱上、下蒙皮应变值总体降低，1号载液油箱段降低比较显著，说明共振对系统响应的影响占主导。晃幅的增加对共振频率激励工况几乎没有影响(工况6和工况8)，而对非共振激励(工况7和工况9)影响较大，上、下蒙皮应变变化剧烈，并引起主应变峰值位置变化。说明共振条件下，振动因素起主导作用，而在非共振激励下，晃动影响相对凸显。工况8和工况10比较可知，共振频率激励下的振幅增加，机翼油箱上、下蒙皮应变均大幅增加，下蒙皮尤其明显。同时共振激励提高了液体运动的惯性，晃动因素的影响也进一步增加，引起主应变峰值位置变化。此外，工况6和工况11对比可知，载液量的减少有效降低了油箱壁面应变幅值，尤其是下蒙皮应变，并对壁面应变分布造成一定影响。

3.4 失效分析

机翼油箱壁面采用碳纤维预浸布和泡沫等复合夹芯结构，本文选取结构稳定响应某时刻的机翼油箱应变结果，利用最大应变准则进行失效分析，给出如图9所示的逆储备因子(Inverse Reserve Factor, IRF)云图，IRF定义如式(9)所示，IRF值越大代表结构越容易失效。可以看出，最易破坏的位置在1号油箱盖与蒙皮连接处和38号贴片点附近位置，次危险区域在靠近翼根处6、7贴片点附近位置。这些危险区域建议加强处理并在适航审定中重点考查。

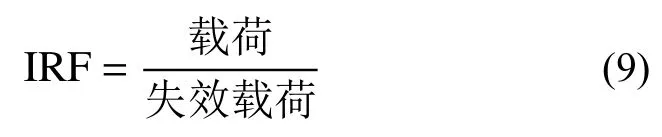
本文同时还考虑了Tsai-Wu、Tsai-Hill、Hoffman和Hashin等复合材料失效准则，如图9所示。Tsai-Wu、Tsai-Hill、Hoffman和Hashin准则下结构IRF分布趋势相似，对应的IRF最大值均在0.35左右，最易发生破坏的位置在38号贴片点附近。最大应变准则的IRF峰值为0.616，说明相同载荷下基于最大应变准则考虑结构更容易失效，最大应变准则评估晃振机翼油箱复合结构失效更为保守。