一种面向异质性时空场数据分析的张量模型

李 冬 双，滕 玉 浩，罗 文,4，俞 肇 元,4*

(1.江苏省作物遗传生理国家重点实验室/江苏省作物栽培生理重点实验室，扬州大学农学院，江苏 扬州 225009;2.江苏省粮食作物现代产业技术协同创新中心，扬州大学，江苏 扬州 225009;3.南京师范大学虚拟地理环境教育部重点实验室，江苏 南京 210023；4.江苏省地理信息资源开发与利用协同创新中心，江苏 南京 210023)

0 引言

地理时空场是空间位置参照和时间参照与属性域之间的连续映射，表征了空间和时间上的连续演化现象。多样的地理要素及其时空演变使地理时空场表现出明显异质性特点[1]，这种异质性体现在维度异质性和分布异质性两方面。其中维度异质性指时间维度、空间维度和属性维度在长度上往往是不均等的，如对于长时间观测序列，时间维上的数据长度则显著大于空间维上的数据长度；分布异质性主要受空间、时间和属性的不同影响，使地理数据在不同区域内呈现出分布不均匀性、空间非均匀性和时间非平稳性，从而表现出结构异质性特征[2]。异质性时空场数据的处理和分析已成为时空场数据分析的热点[3]。

现有时空场数据模型主要包括时空立方体模型、点云模型和参数化模型3类[4]。时空立方体模型可看作是由一系列规则栅格堆叠而成的多维矩阵，该类数据模型在规则时空场表征上有优势，但在时空场对象检索、不同维度重组以及数据分析等方面的复杂度较高[5]；点云模型类似于时空点对象，为包含多个属性值的多维点集结构，该类模型可有效进行维度扩展和组合，但由于各质点间关系模糊、结构性差，不利于复杂的时空特征分析方法的构建[6]；近年来，基于参数的场表达与分析在物理学、工程应用等领域得到较大发展[7,8]，参数化模型多适用于结构规律性强、机理过程相对明确的时空场的表征，但地学时空场数据往往表现出显著的多尺度叠加的异质性特征，机理过程不明确，导致参数化模型在地理时空场表达中应用不多[9]。上述3类时空场模型多立足于对现有空间数据模型的时域拓展，在高维数据表达以及异质性的时空数据分析支撑方面尚显薄弱。

张量是矩阵的高维扩展，可用于多变量、多坐标系统对象的统一表达，是进行地理时空场数据组织的有效工具。张量结构的多维表达特性为时空场数据的表达提供了原生数学支撑。张量分解则通过对张量数据进行投影映射，利用线性或层次化的结构将高维时空场转换成低维的张量、矩阵或向量[10,11]，实现对时空场中数据特征的解析和提取，可以挖掘不同维度数据间整体的耦合作用关系，并有效支撑时空场数据的组织和特征分析，已广泛应用于地理时空场数据特征提取、组织管理以及可视化分析等方面[12,13]。然而，经典的张量分解模型主要利用矩阵化方式进行降维，进而在降维矩阵上通过诸如矩阵分解等方法进行特征提取。准确的张量分解多依托于两类假设：1)观测数据在不同维度上的数据长度相对一致[14]，该假设是为保证张量矩阵化后，不会因为矩阵在不同维度上数据长度差异过大导致矩阵分解获得的特征存在明显偏差；2)观测数据的数值分布相对均一，不存在显著的结构差异或突变[15]，该假设可保证在张量矩阵化后，矩阵分解方法可提取出稳定的特征分量。但异质性的地理时空场数据多难以满足上述两类假设，影响张量在异质性地理时空场数据分析中的适用性[16]。

从数据投影和数据分块的视角对此类数据进行局部拆分，进而利用张量算子建立从局部到整体的特征分析框架，是解决异质性张量特征分析问题的可行途径。但数据的拆分不仅需要考虑原始时空场数据的组织管理，还需要考虑不同的数据投影或拆分结果，以及在张量分解过程中产生的过程数据的组织与管理。因此，从拆分的视角构建异质性时空场数据的张量数据模型易导致时空场数据模型构建的复杂性，需要在现有张量分析的基础上，通过有效的数据组织和变换，建立适用于异质性时空场数据分析的张量模型。鉴于此，本文将张量引入异质性时空场数据模型设计，研究基于张量的异质性时空场数据的组织表达方法，结合不同类型的异质性时空场数据特点，基于面向对象设计不同类型的异质性时空场数据类、类中包含的属性和操作以及不同类之间的逻辑关系，以期实现面向异质性时空场数据分析的张量模型构建；在此基础上，以维度非对称数据和结构异质数据特征提取为案例，分析所构建模型对支撑异质性时空场特征提取的优势。

1 基于张量的时空场数据组织与操作

1.1 基于张量的时空场数据组织模型

基于张量的时空场数据组织模型需要考虑时空场数据所具有的维度不规则和分布不规则的特性(图1)。对于维度非对称数据，其不仅具有常规时空场数据的多维特性，且各维度数据长度差异较大。因此，为能从多维度联合解析，同时也能有效兼顾各维度的差异性，可以引入维度集合拆分的思路。对于给定的张量形式表达的时空场数据A∈RX×Y×T，其数据维度集合{X,Y,T}可拆分为不同的维度组合{X,Y},{X,T},{Y,T}。原始张量数据可以被投影到这些不同维度组合上，形成一系列的维度子空间进行数据组织。这些维度子空间不仅包含所有可能的维度组合，同时还可以从局部维度视角透视原始数据。由于这些维度子空间维度较低，且其各维度上的数据长度相较于原始数据更加均衡，因此，综合不同维度子空间透视原始数据，可以削弱维度不规则对于数据整体特征揭示的影响。

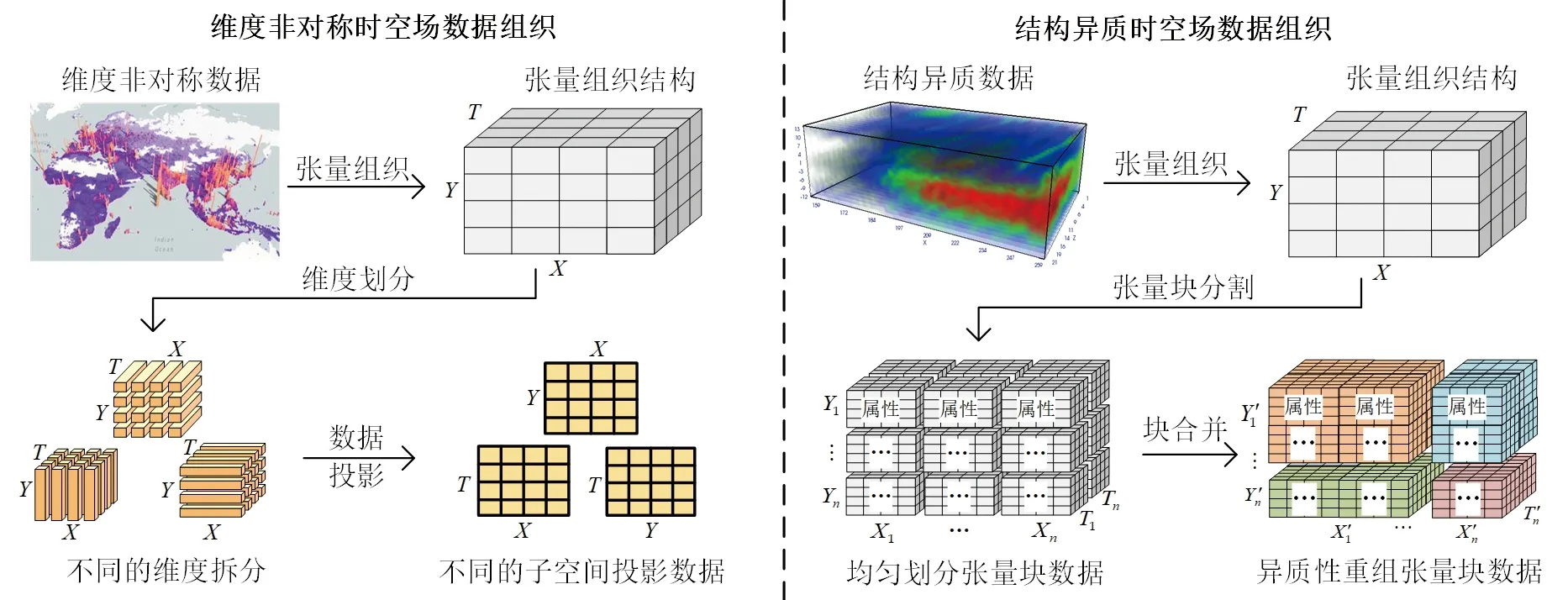
图1 基于张量的异质性时空场数据组织Fig.1 Tensor-based organization of heterogeneous spatial-temporal field data

对于结构异质时空场数据，其不仅具有常规时空场数据的多维特性，而且其各个局部结构差异较大，因此，需要有效兼顾数据整体的多维性和内部结构的差异性。借鉴数据划分—合并的思想有助于降低数据内部分布的异质性。对于张量表达的时空场数据A∈RX×Y×T，可将其分割成大小一致的子张量块{A1∈RX1×Y1×T1,A2∈RX2×Y2×T2,…,An∈RXn×Yn×Tn},构建子张量块相似度度量ρi,i+1=similarity(Ai,Ai+1)，similarity( )为相似度计算函数，由于数据的分量既可以是向量形式，也可以是矩阵形式，因此所使用的相似度计算函数可以分别采用余弦相似度和皮尔逊相关系数等实现，并结合相似性阈值(α)将子张量块合并。张量块的合并是一个迭代过程，合并的张量块会根据判断准则决定是否继续与相邻块合并。具体而言，若ρi,i+1≥α，则Ai={Ai,Ai+1}，即将子张量块数据沿着某维度追加;若ρi,i+1<α，则Ai和Ai+1仍然组织为独立的两块。基于上述规则对原始数据进行重组后，其每个局部子张量块数据内部的特征相似，而相邻子张量块的特征差异较大。因此，可以在每个局部子张量上进行特征分析，而后合并获得整体张量的特征结构。

1.2 基于张量的数据操作与分析流程

以张量为基础，构建具有灵活的维度运算特性和高维特征分析能力的张量算子，可以有效支撑张量的数据操作和运算。面向异质性时空场数据操作，本文构建了表1所示的张量数据操作算子，其中张量的维度拆分、数据投影和相似度计算等算子主要用于实现异质性时空场数据的子空间构建、张量分块、张量合并等操作。考虑到高维相似度测算通常较为困难，本文设计的相似度算子首先利用张量分解得到低维特征分量，进而通过分量间相似度计算函数估计高维数据的相似度。数据投影算子类似于二维矩阵中的特征分解，对于高维数据，则可利用张量分解算子实现高维异质数据各维度特征的提取，进而利用张量重构算子实现对异质性时空场数据不同维度的透视[17]。相较于传统的矩阵分析，基于张量分解的数据操作可以避免传统方法中诸如数据向量化造成的维度灾难[18]。通过在张量框架下构建异质性时空场数据的数据操作算子，可降低由时空场数据特性差异导致的数据操作复杂性。

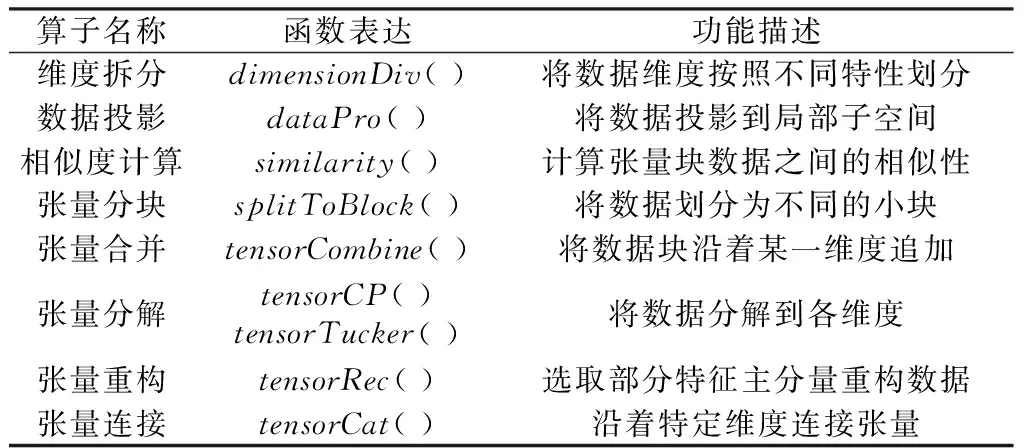
表1 基于张量的数据操作Table 1 Tensor-based data manipulation

以张量算子为基础，构建异质性时空场组织管理和时空分析的流程如图2所示。在数据组织方面，将观测到的异质性时空场数据，根据时空特征组织成高阶张量的形式，依据不同异质性时空场的类型，构建出对应类型的组织模型；在数据操作方面，将张量分块、合并等操作贯穿于整个数据组织和分析过程中，通过算子定义的方式实现各类张量操作的函数化和算子化，以适应不同类型时空场数据的操作；在数据分析方面，利用张量分解得到异质性时空场数据沿经度、纬度、时间的变化特征，利用张量积运算即可重构出经度与纬度、经度与时间、纬度与时间上的特征分布。

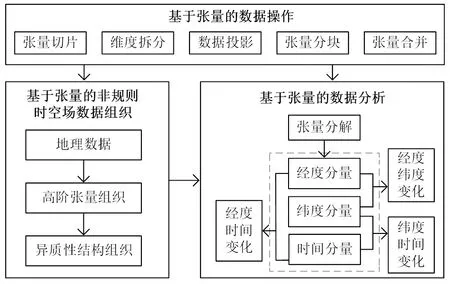
图2 数据模型构建流程Fig.2 Data model building process

2 异质性时空场数据模型设计与实现

由于异质性时空场数据的张量表达在不同类型数据之间存在差异性，为简化不同数据之间处理和操作的难度，利用面向对象思想中的封装、继承与多态等特性进行异质性时空场数据模型的构建。首先，由于异质性时空场数据的结构比较复杂，且涵盖不同类型，需要根据规则化的数学描述对不同类型的异质性时空场数据进行完备的张量描述，其不仅能够描述常规张量的特性，还应包含一些典型的异质性特征，以便后续在这个规范化的数学描述体系上架构分析方法。再者，考虑到异质性时空场数据的结构特殊性，常规的张量分析方法无法直接应用，一个可行的方法是利用算子构建，将异质性时空场数据尽可能地规则化，在此基础上，考虑将其与常规张量分析方法相结合，构建适用于异质结构张量的数据分析方法。本文定义了数据模型中的类、类中包含的属性和操作以及不同类之间的逻辑关系，即异质性时空场数据模型的UML(Unified Modeling Language)(图3)。

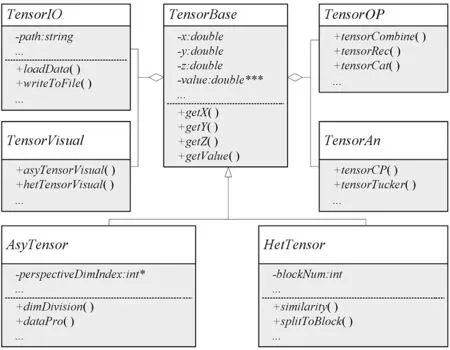
图3 异质性时空场数据的UML图Fig.3 UML diagram of heterogeneous spatial-temporal field data

该数据模型中，异质性时空场数据模型通过基类TensorBase、文件操作类TensorIO、数据操作类TensorOP、数据分析类TensorAn与数据可视化类TensorVisual实现对时空场数据的传输、计算分析与可视化；继承基类TensorBase，衍生出两个子类，分别为维度非对称张量类AsyTensor以及结构异质张量类HetTensor。其中，基类TensorBase通过众多变量实现对异质时空场的描述，并聚合TensorIO、TensorOP、TensorAn与TensorVisual类实现对异质时空场的计算和分析，继承基类的子类可以对方法进行继承或重写，为不同数据类型提供统一的接口；文件操作类TensorIO包含数据的读入与输出;数据操作类TensorOP贯穿于整个数据模型的建立过程中，包含张量重构、合并、连接等运算；数据分析类TensorAn定义了常用的特征提取方法，如张量Tucker分解、张量CP分解、主成分分析等，用于异质性时空场规则化之后的特征提取。子类AsyTensor以及HetTensor分别用于存储维度非对称和结构异质时空场数据，其不仅继承或重写了基类TensorBase的属性与方法，还包含具有自身特点的方法，如非对称数据的维度拆分方法dimDivision( )以及结构异质数据的数据合并方法tensorCombine( )等。最后利用数据分析类TensorAn中定义的方法，完成对异质性时空场数据的特征提取，并通过算子的重载以满足不同类型张量分析的算法。具体实现流程(图4)为：通过文件操作类TensorIO获取数据，根据异质性类型，通过调用对应子类中的方法，将异质性时空场组织成规则的张量，进而通过TensorAn中定义的分析方法完成异质性时空场的特征提取。

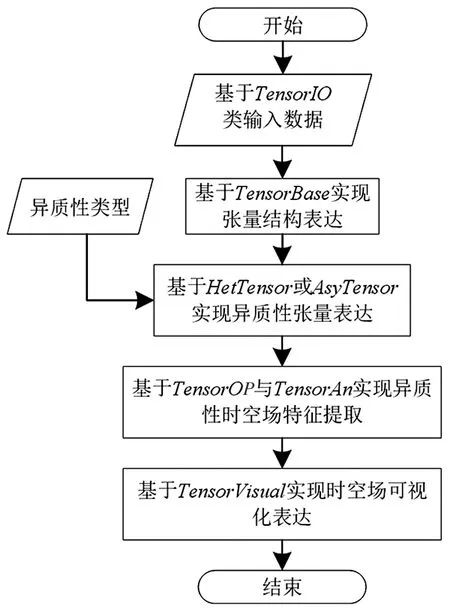
图4 异质性时空场数据分析步骤Fig.4 Steps for analysis of heterogeneous spatial-temporal field data

3 应用案例

3.1 数据组织

基于C++语言建模与构建分析系统，编写基于张量的异质性时空场数据模型以及相关操作方法，构建系统底层API；GUI层基于Wxwidgets架构，并利用VTK(Visualization Tool Kit)实现基于张量的异质性时空场数据的可视化表达。为验证本文提出的基于张量的异质性数据模型的优势，选取NOAA(https://psl.noaa.gov/data/20thC-Rean/)发布的多气候模型融合形成的气象再分析气候模式数据构建验证实验。NOAA再分析数据只是数据本身，实验分别对维度非对称数据和异质性数据进行建模，其对应数据模型中AsyTensor类和HetTensor类，并将基于张量的数据模型的分析方法与基于传统时空数据模型的分析方法进行对比。

3.2 异质性时空场数据分析

面向典型的异质性时空场数据，基于TensorIO读取数据。依据输入时空场的异质性类型，将原始数据组织成对应类型的子类张量，并调用子类中对应的方法完成数据的规则化，进而调用TensorAn中的方法完成特征提取，如张量CP分解tensorCP( )、张量Tucker分解tensorTucker( )等。

3.2.1 维度非对称时空场数据分析 对于维度非对称时空场数据，为便于构建不同维度组合下的子空间，应尽可能多选取数据集的维度数。本文选取包含经度维、纬度维、高度维和时间维的四维数据集(空间分辨率为2°×2°)，并将其存储为(经度×纬度×高度×时间)时空场数据Air1∈R180×90×24×756，该数据空间与时间维度上数据长度差异较大，存在明显的维度非对称性。维度非对称时空场数据的特征提取方法(算法1)实现流程为：首先将原始时空场数据按照不同维度组合进行切片，然后计算切片数据的信息熵并进行数据降维，得到不同维度组合下的子空间，应用主成分分析等方法得到降维后各子空间数据的特征结果。

算法 1:维度非对称时空场数据的特征提取方法

Input:Spatio-temporal field data (STField) with imbalanced dimensions,the dimensions that need to be analyzed.

Output:A series of features ofSTFieldfrom the dimensional perspectivesI,J...

1.slice=tensorSlice(STField,I,J…);//沿着给定的维度I,J…切割数据STField

2.entropy=getEntropy(slice);//计算切割后数据的信息熵

3.reduction=tensorReduction(STField,I,J…,entropy);//降低数据维度，使降维后数据只与给定的维度有关

4.feature=PCA(reduction);//对降维后数据应用主成分分析

5.returnfeature;

为验证本文维度非对称数据模型的优势，将基于维度子空间组织的特征分解与直接基于原始数据的特征分解进行对比。其中，Air_Tucker与Air_CP分别为直接对原始数据进行张量Tucker分解与张量CP分解的结果，Air_PCwx为对基于维度子空间组织的张量分解结果。为验证这些特征分量与厄尔尼诺南方涛动(ENSO)事件的对应性，选取表征ENSO事件强度的MEI(Multivariate ENSO Index)分别与所提特征分量进行对比，并计算对应的相关系数。从特征曲线对比看(图5)，本文方法提取的特征曲线在周期和走向上与MEI指数的对应性较好，Air_PCwx、Air_Tucker和Air_CP与MEI的相关系数分别为0.697、0.259和0.137，表明本文方法可以更精确地解析ENSO信号。但CP分解在2001年以后，曲线走向与MEI相比发生明显偏差；Tucker分解在1950-1965年之间，较MEI指数呈现出较大的偏差。

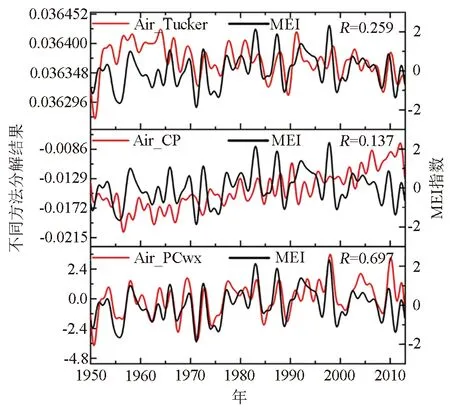
图5 不同方法的分解结果对比Fig.5 Decomposition result comparison of different methods

3.2.2 结构异质时空场数据分析 对于结构异质时空场数据，为便于数据块切割，从简单的三维数据进行尝试。因此，选取的时空场数据集在高度上只取表层(空间分辨率为2.5°×2.5°)，并将数据集存储为(经度×纬度×时间)时空场数据Air2∈R144×73×365。由于该数据是多年平均数据，容易受全年不同时期的气候事件影响，在时间上呈现出结构异质的特点。构建结构异质时空场数据的特征提取方法(算法2)实现流程为：首先将原始数据切割为一系列的数据块，并计算相邻块之间的相关系数，根据相关系数结果和给定的阈值，将数据块进行重组(图6)。由于重组后数据块的内部结果相对一致，因此在每个重组数据块上应用张量分解可以很好地提取出该类数据的整体特征，同时也有助于消除由数据差异导致的估计偏差问题。

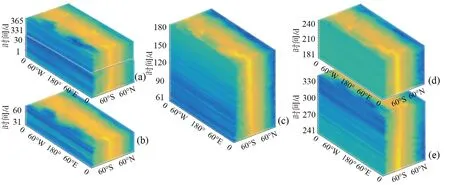
图6 异质性时空场数据组织Fig.6 Organization of heterogeneous spatial-temporal field data

算法2:结构异质时空场数据的特征提取方法

Input:Spatio-temporal field data (STField)with heterogeneous structure

Output:A series of features of the sub-tensor block ofSTField

1.block1,block2,block3,…,blockn=tensorDivide(STField);//将数据STField切割为一系列的块

2.p1,2,p2,3,…,pn-1,n=similarity(block1,block2,block3,…,blockn);// 计算相邻数据块之间的相似性

3.subTensor1,…,subTensorn=tensorCombine(block1,block2,…,blockn,p1,2,p2,3,…,pn-1,n);// 根据相似性重组数据块

4.int i=0;//对重组后的数据块单独应用张量分解

5.whileiisthenumberofsubTensordo

6.feature=tuckerDecp(subTensori);

7.add feature tofeatrueList;

8.returnfeatrueList;

为验证本文结构异质时空场数据模型的优势，将基于张量块数据模型的张量分解(简称为局部分解)和直接基于原始数据的张量分解(简称为整体分解)结果进行对比，并绘制这两种分解结果在各维度上的相对误差率如图7所示。从误差的整体比较看，局部分解结果在时空维度上的相对误差率均小于全局分解的相对误差率，说明基于所构建的分块数据模型的张量分解可以显著提高异质性变化显著数据的特征估计的准确性，且误差分布更平稳。

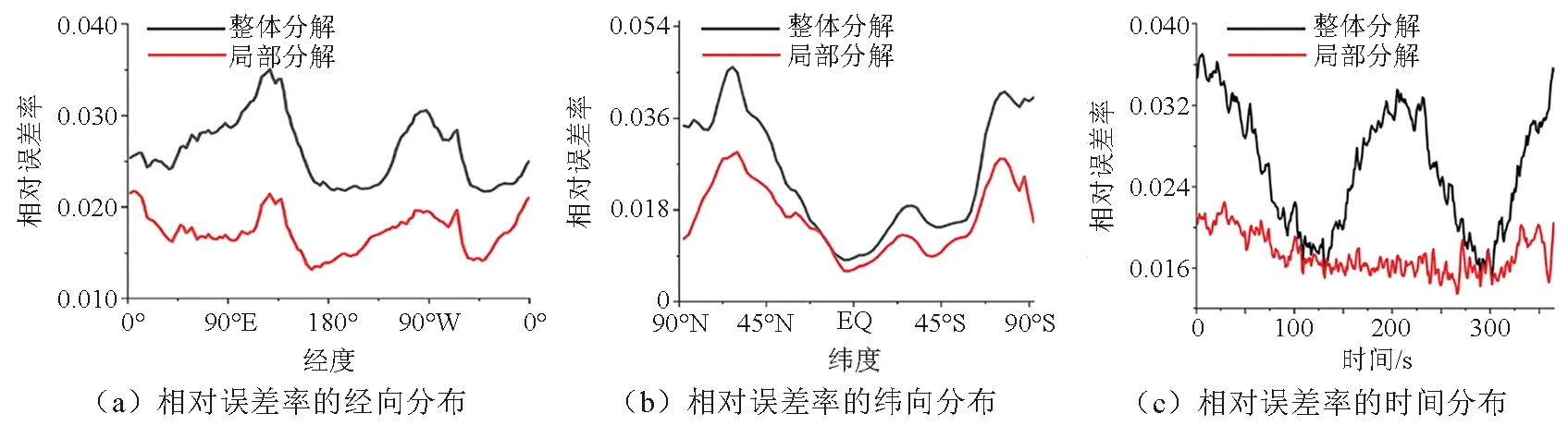
图7 不同分解方法的相对误差率对比Fig.7 Relative error rate comparison of different decomposition methods

从上述两类典型的非规则时空场数据的分析流程看，相较于传统张量分析，基于所构建数据模型的时空分析方法在原始张量分解基础上，增加了数据切片、分块、合并等复杂度较低的数据操作，此类操作的计算复杂度相较于张量分解过程中所涉及的大型矩阵的计算复杂度几乎可以忽略不计。从时间复杂度上看，对维度非对称张量计算复杂度影响较大的主要是子空间划分的规则和规模。仅就本文所使用数据的分析结果看，Air1数据的维度非对称张量分解虽较传统的张量分解耗时多2.01 s，但对ENSO等复杂信号的揭示更加精确。 而对异质性时空场数据，其计算复杂度主要与数据分块的模式(分块数和分块的大小)有关，其中数据分块模式取决于数据的异质性特征，即依赖于具体的数据。在本文设计中，分块模式需要根据相似度计算函数和相似性阈值确定。仅就本文所使用数据的分析结果看，Air2数据的最佳分块数是5，总的分块及分解时间为2.27 s，整体分解时间为5.88 s。整体效率的提升是由于切割之后的张量数据块更小，每块在张量分解时耗时更短。因此，分块张量分解不仅对原始数据逼近得更加精确，而且比传统张量分解耗时少。

4 结语

本文针对现有张量分析在支撑异质性时空场数据所面临的特征估计偏差等问题，利用张量结构对高维数据的支撑特性和张量算子的维度融合特性，从局部到整体的分析视角出发，建立了涵盖张量子空间和张量块结构的异质性时空场描述模型和操作算子。结合面向对象思想设计了不同类型的异质性时空场数据类、类中包含的属性和操作以及不同类之间的逻辑关系，构建了异质性时空场数据模型。基于气象再分析实验案例表明，该数据模型可有效支撑异质性时空场数据的组织，而且在支撑时空场数据分析方面，比传统张量方法的特征估计精度更高。

本文所提数据模型直接面向高维异质时空场数据，为异质性较强的时空统计方法的高维推广提供了有利借鉴。在应用支撑上、可为机器学习、关系推断和微弱信号的提取和滤波，以及更精细数据的时空分区、耦合关系计算和作用机制的计算等领域提供方法借鉴。未来继续突破的工作包括：1)数据的异质性特征测度体系构建；2)地理时空场异质性类型的自动识别和分类；3)融合数据特征的异质性时空场数据的自动分块策略构建。