基于球缝模型优化反演的裂缝储层评价新方法

刘诗琼， 石强， 汤继周， 刘堂晏*， 赵文君， 陈鹏

1 西南石油大学油气藏地质及开发工程国家重点实验室， 成都 610500 2 同济大学海洋地质国家重点实验室， 上海 200092 3 中国石油勘探开发研究院， 北京 100083

0 引言

绝大部分裂缝储层实际上都包含裂缝和孔隙两个基本的储层储集和渗流的空间.在真实的裂缝储层中，裂缝的形态、数量以及裂缝和孔隙之间的配置关系千变万化、裂缝的形态发育非常复杂，这些因素的相互作用，导致准确客观评价裂缝储层非常困难.评价裂缝储层的主要内容包括裂缝孔隙度、裂缝形态及空间展布、裂缝与孔隙的配置关系等.由于裂缝形态，以及裂缝与孔隙的配置关系异常复杂，到目前为止，尚无精确解析数学模型完成以上相关的裂缝储层评价与计算分析.从裂缝储层评价方法属性的角度进行分类，可以分为三类，数值统计分析、模型模拟分析和人工智能分析.数值统计分析的研究方法，主要使用大量的各种数据，采用统计方法研究裂缝储层的发育规律.Nazemi 等(2021)把目标储层按照沉积序列关系分成8个亚类型，之后，按每个亚类分别确定各自的饱和度指数(n)，采用这样的裂缝储层评价方法，可以显著提高裂缝储层的计算饱和度精度.Golsanami等(2020)用实验的方法，研究岩石弹性参数、Archie公式参数之间的关系，以及岩石弹性参数对于裂缝发育的影响.在岩石物理实验数据研究和三维颗粒流体代码(Particle Flow Code 3D，PFC3D)数值模拟的基础上，发现杨氏模量与岩石胶结指数之间具有很好的相关性.Nazemi、Golsamami等的研究工作可以归属为数值统计分析的研究方法.在致密含气储层中，裂缝和断层的发育形式、发育程度和分布范围对于形成页岩气的优势通道具有至关重要的作用.在多数情况下，裂缝渗透性对于储层流体的渗流能力起到主要的控制作用，而孔隙渗透性对于储层流体的渗流能力只有次要的控制作用(Rashid et al.，2021).正是由于储层裂缝系统的极端复杂性，采用传统的数学解析方法不能有效描述裂缝形态和空间展布的渗流特征，Silva等(2021)建议采用拓扑学的方法，研究储层中裂缝发育形态和分布规律，其研究证明裂缝系统内部的相互连通程度和方式，对于储层的综合渗透率具有非常显著的作用.考虑张开裂缝的宽度，可以预测裂缝改善渗透率的产液剖面(Nabiei et al.，2021).裂缝性储层发育，还经常与页岩气及致密气的工业开采措施有关，而页岩气或致密气的价值，取决于单位储层岩石中的含气丰度及页岩气“甜点”的展布范围(夏宏泉等，2021)，所以，根据单井解释的含气储层及页岩气“甜点”必须具备一定的展布范围，致密气及页岩气开采才具有工业价值.聂永生等(2013)关注了这个问题，由于测井数据本身的局限性，测井数据难以描述井筒周围1.5 m以外的裂缝发育形态，把地震、测井、岩心结合起来，建立裂缝发育体系的三维模型，该三维模型对裂缝发育强度、裂缝发育角度及裂缝发育形态(闭合/张开)、裂缝渗透率进行了全空间的刻画.地层微电阻率扫描图像(FMI)也是一种评价裂缝储层的有利手段，结合常规测井资料，可以根据FMI图像区分裂缝的发育类型(闭合裂缝、张开裂缝)、地层的层理面.Boersma等(2020)及张立安等(2020)报道了类似的研究工作，其主要内容是利用FMI刻画裂缝的发育形态和张开度.另外，井壁上裂缝纵横比也是刻画裂缝延展范围的关键参数.应用声波测井资料，基于Gassmann模型，反演得到裂缝孔隙纵横比谱分布，根据裂缝孔隙纵横比谱计算的裂缝孔隙度较真实地反映裂缝的发育形态，与电成像测井刻画的裂缝特征比较吻合(陆云龙等，2019).Salifou 等(2021)基于孔隙类型划分的方法，将储集空间划分为裂缝、基质孔隙(matrix porosity)和孔洞孔隙(Vugs)，综合常规测井和成像测井，建立了针对塔里木研究工区的裂缝储层评价模型.模型模拟分析的研究方法，主要特点是抽取裂缝储层的主要刻画参数，采用正演反演的方法，建立刻画裂缝储层的模型，并依据模型的计算结果开展储层发育特征评价.Ren等(2020)采用有限元的方法，模拟储层岩石在地下应力场和钻井泥浆柱压力共同作用下，井周裂缝的生成和扩展方式.Ren等(2020)和Tang 等(2018, 2019)研究发现，杨氏模量和泊松比是裂缝延展的主要控制参数.Taghipour等(2021)从天然气开发导致地层压力损失的角度，研究重新注气维持储层压力，并引起断层重新活动的程度和活动方式.Ren、Tang和Taghipour等人的研究可以归属于模型模拟这一类的研究方法.人工智能的分析方法，主要采用深度学习、自适应反演等新型研究方法，展开裂缝储层评价，近10年来，这类研究方法日趋活跃.在简化或不简化模型参数的情况下，机器学习、人工智能是裂缝储层评价的有效手段(刘坤等，2018；陈芊澍等，2021).

分析现有的研究报道，发现研究人员主要从整体上、宏观上刻画储层裂缝的发育形态和展布区间，缺乏从微观上研究裂缝发育形态、裂缝发育程度的文献报道.核磁测井作为一种新型高技术含量的测井方法，其对于裂缝发育形态和储层孔隙空间非均质性、渗滤特征具有很好的刻画能力.

本文研究把裂缝储层中的孔隙形态归结球形孔和裂缝两种基本类型，提出了基于球缝模型的裂缝储层评价模型.根据这一模型，发展了针对核磁测井回波优化反演的算法，计算得到裂缝储层的孔隙结构参数.在本次研究的工区中，孔隙结构参数与储层岩心分析物性参数具有较好的相关性，并能刻画实际产层的裂缝发育特征，在页岩气甜点识别、以及在射孔选层和压裂改造层位优选等研究工作中均具有很好的应用前景.

1 球缝模型及刻画方程

首先，把裂缝储层的基本储集空间归结为球形孔和裂缝两种基本类型，然后，由裂缝与球形孔叠加成球缝模型(图1).根据球形孔和裂缝尺寸配置关系的变化，形成核磁回波反演布点的计算方法.在此基础上，形成核磁回波的优化反演算法，并根据优化反演结果，计算裂缝宽度、球形孔半径，以及裂缝和球形孔的数量分布等.即在优化反演的基础上，实现考虑孔隙结构的裂缝储层定量评价.

图1 球缝模型参数关系

如图1所示，裂缝与球形孔组成球缝模型，可以推导球缝模型的描述公式：

(1)

其中，h为球冠的高度，μm；Rf为裂缝的半宽度，μm；Rs为球形孔的半径，μm；Cd为裂缝半宽度与球半径的比值(Rf/Rs)，无量纲；r为球冠的底圆半径，μm；Ss为球冠的表面积，μm2；Vs为球冠的体积，μm3；T2i，T2max，T2min分别为核磁回波反演布点的第i个横向弛豫时间、最大和最小横向弛豫时间，ms；Rei为等效球的半径，μm；ρ2为横向弛豫率，cm·ms-1.

(2)

从方程(2)可以看出，Rs是Re、Cd的函数.根据方程(1)，用T2的布点值方程计算Re.那么，计算Rs唯一的未知数是Cd.当Cd确定后，Rs、Rf均可用方程(1)计算出来，即可以确定储层的孔隙结构.

在确定Rs、Rf后，分别计算球缝模型中的球形孔、裂缝的表面积和体积(方程(3))，因为每个球缝模型包含2个球冠(图1)，所以，球形孔表面积和体积分别是球冠表面积和体积的2倍.

(3)

有2个特殊情形需要单独加以考虑.首先，Cd=1时，模型退化为全裂缝，相应模型方程修改为：

(4)

其次，当Cd=0时，球缝模型退化为纯球形孔，可以得到退化球缝模型的描述方程：

(5)

球缝模型的算法流程是：

首先，应用方程(1)中的T2i表达式，计算一个初始的核磁回波反演布点值.

第二步，假设一组Cd值，根据T2i划定分组区间，应用方程(2)和方程(1)，计算每个分组区间Rs和Rf.

第三步，针对每个分组区间，联合方程(1)和方程(3)，计算每个分组区间中的Vs、Vf、Ss和Sf.

第四步，应用表面弛豫的计算公式(6)，重新计算每个分组区间的横向弛豫时间布点值，

(6)

第五步，反演核磁回波数据，并计算反演拟合的均方差：

(7)

式中，σ为反演拟合方程的均方差，无量纲；i为回波的采集序号；Yi为第i个观测的核磁回波信号，无量纲；j为核磁回波反演的布点个数序号，可改变；Aj为T2谱分布的相对幅度，无量纲；M为采集回波的个数，本文M=2048;T2j为第j个分组孔隙的横向弛豫时间，ms；ti为第i个回波采样的时刻，ms.

第六步，重复第二步至第五步，并记录每次重复反演回波信号与拟合方程之间的均方差.当均方差达到最小值时，与Cd数据组对应的Rs、Rf，就是岩石样品内部孔隙结构的最优描述参数.

从建立球缝模型的优化反演算法可知，设计不同类型的Cd数据组，并力求使设计的Cd数据组反映岩石内部真实的孔隙结构，是实现球缝模型优化反演核磁回波的关键.薛苗苗等(2014)在讨论球管模型优化反演核磁回波的研究中，提出一种Cd路径扫描的方法，确定每个孔隙分组中的Cd值.本文用此方法确定球缝模型优化反演的分组Cd值(图2).

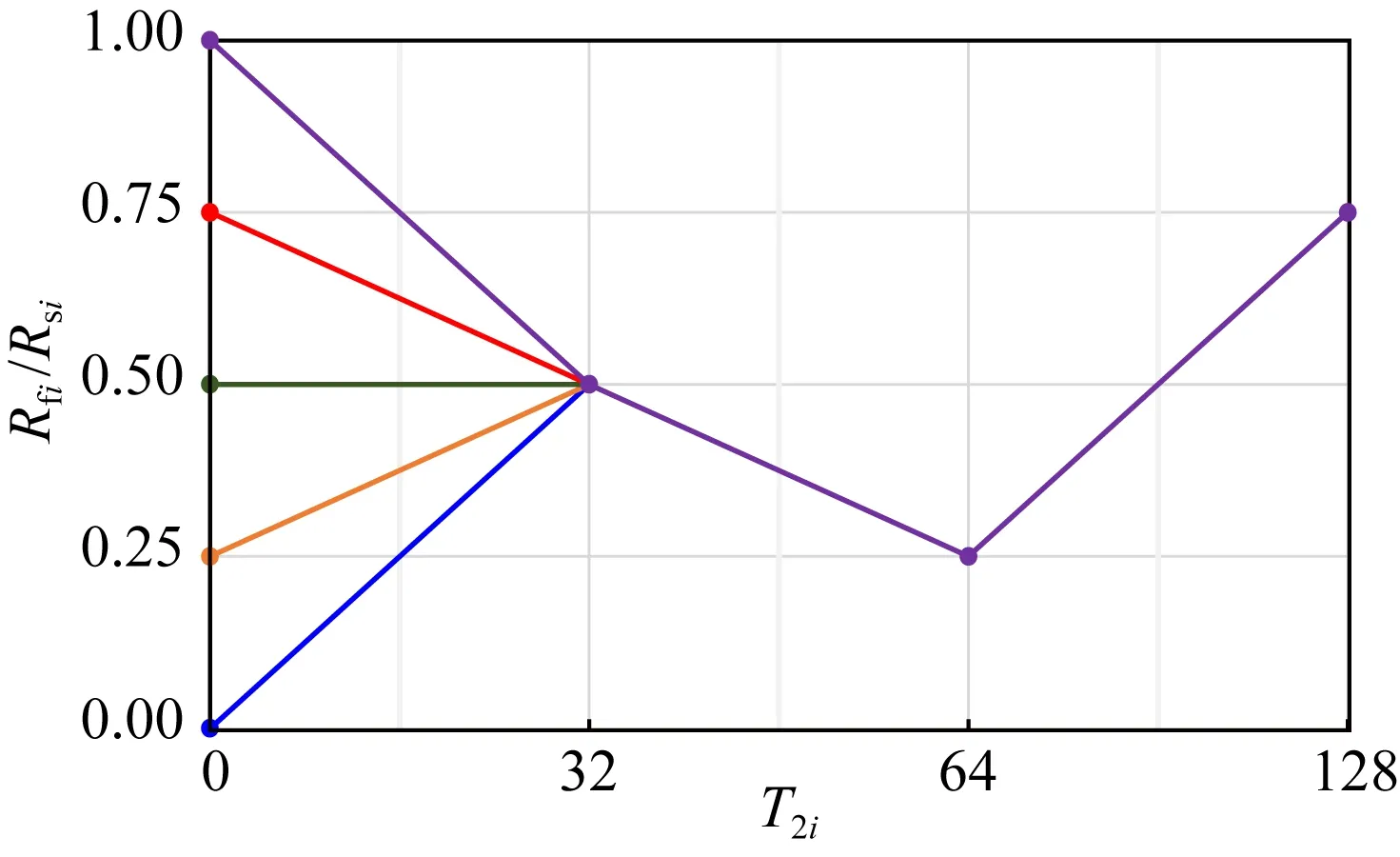
图2 球缝模型优化反演寻优路径示意图

图2中横轴是布点的编号，纵轴是Cd值.如果采用128个反演布点，图中每一条折线的横轴坐标值就是布点的编号，纵轴坐标值就是Cd值.当沿任一折线从左向右扫描时，折线上每个布点编号对应的纵坐标，就是该分组中裂缝与球形孔匹配的Cd值.沿不同的折线从左向右扫描，即假设岩石中具有不同孔隙结构形态.当沿着某一条折线确定的分组Cd值，计算得到横向弛豫时间(T2)的反演布点，在这个布点值下反演核磁回波数据，回波数据与拟合方程之间的误差达到最小值时，这个孔隙分组的Cd值就近似刻画了岩石内部的实际孔隙结构，即裂缝与球形孔之间的匹配关系(刘堂晏等，2006).

根据图1的球缝模型概念图，当裂缝的宽度大于等于球形孔直径时，规定Cd=1，为球缝模型的第一个退化形式，即纯裂缝模型；当裂缝宽度为零时，根据Cd值的定义得到：Cd=0，为球缝模型的第二个退化形式——纯球形孔模型.当Cd值定义域位于[0,1]之间时，根据Cd值的物理意义和Cd路径扫描的方法，应用优化的Cd路径扫描结果，可定性判断岩石中的孔隙结构.即Cd路径接近1时，说明储层中裂缝增加；Cd路径接近0时，说明岩石中球形孔增加.本文用此方法，定性判断岩石中孔隙结构的变化.

2 实用反演算法简介及实现流程

NMR数据处理重要步骤之一是根据核磁回波数据反演得到T2弛豫时间分布.通常，岩石T2弛豫时间分布是一个连续函数，为简化计算，将T2弛豫时间离散化，王为民等(2001)提出多指数模型拟合核磁回波数据的反演算法(方程(8)).

Y1=f1e-t1/T2,1+f2e-t1/T2,2+…+fne-t1/T2,n,

Y2=f1e-t2/T2,1+f2e-t2/T2,2+…+fne-t2/T2,n,

⋮

Ym=f1e-tm/T2,1+f2e-tm/T2,2+…+fne-tm/T2,n,

(8)

其中，Y1,Y2,…,Ym为核磁回波幅度标准值，无量纲；m为核磁回波的个数；T2,1,T2,2,…,T2,n为横向弛豫时间反演布点值，ms；n为横向弛豫时间反演的布点个数；f1,f2,…,fn为T2谱分布的幅度值，无量纲；t1,t2,…,tm为核磁回波的采集时刻，ms；A为反演系数矩阵.

写成矩阵形式：Y=AF.核磁回波数据的反演结果证明，由于系数矩阵A具有很大的条件数(conduction number)，核磁回波数据的微小扰动，都能造成方程解的极大波动，因此，求解这个方程是一个严重的病态问题(翁爱华等，2003；谢然红等，2009).

2.1 Tikhonov-TSVD法

Tikhonov正则化方法(Butler et al.，1981；Hansen and O′Leary，1993；Regińska，1996)是目前解决病态问题应用最为普遍的一种方法，其估算准则为：

OF=‖Af-d‖2+ε‖Lf‖2=min.

(9)

该目标函数兼顾数据方差项和模型长度项联合确定最小值，其中，ε为正则化因子，控制残差和解的约束大小的权重.很多情况下，可以把“L”型曲线的拐点位置作为ε值的选择依据(王飞飞等，2016).将该目标函数对f求偏导数，并令其为零，得到正则化解：

freg=(ATA+εI)-1ATd.

(10)

不考虑正则化因子，则正则化解变成最小二乘(LS)解：

fLS=(ATA)-1ATd.

(11)

一般采用奇异值分解(SVD)算法求解方程(10)或方程(11)(王为民等，2001；姜瑞忠等，2005；林峰等，2009)，但是，奇异值衰减非常快，其结果是：观测数据中很小的误差都将使得最小二乘解显著地偏离真实值.实际测量的回波数据一般信噪比不高，因此，在实际计算过程中，可以设置一个阈值，将小于阈值的奇异值赋值为零，增加最小二乘解的稳定性，达到消除方程病态的目的(图3).

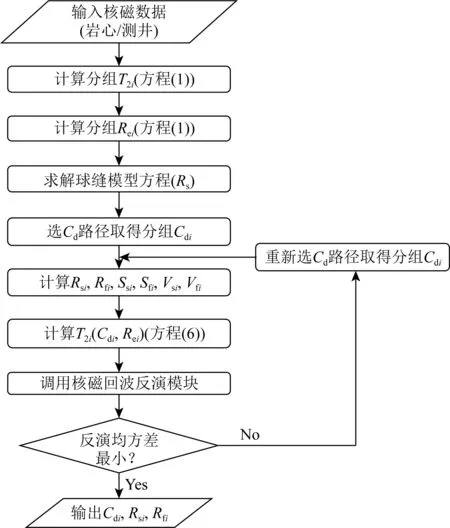
图3 核磁回波反演算法

就孔隙分组的物理意义而言，T2谱分布的幅度对应孔隙分组的相对份额，所以，孔隙分组的数值必须大于或等于零，即方程(10)确定解的全部分量值大于或等于零.对于出现小于零的分量值，需要去掉该孔隙分组对应的反演矩阵系数列，并重新计算方程(10)解，直到全部的解分量大于或等于零(王为民等，2001；姜瑞忠等，2005；林峰等，2009).

2.2 球缝模型优化反演实现流程

将建立的球缝模型优化算法(图3)及Cd路径的扫描方法，写成优化反演程序，实现球缝模型优化反演核磁测井回波数据，得到储层孔隙结构参数(图4).

3 球缝模型优化反演算法的应用

在研究工区应用球缝模型优化反演算法，对12口井的核磁回波数据进行处理，得到储层球形孔谱和裂缝谱，再基于这两种谱计算球形孔均值半径、裂缝宽均值、球形孔和裂缝的分选系数、球形孔和裂缝的峰态等孔隙结构相关的参数(罗蛰潭和王允诚，1986，图4).

3.1 孔隙结构参数与储层物性的关系

在对核磁回波完成优化反演之后，得到孔隙结构参数：球形孔均值半径、裂缝宽均值半径、球形孔和裂缝的分选系数、球形孔和裂缝的峰态等(图4).研究孔隙结构参数与岩心分析物性参数之间的关系，以及对储层物性的刻画方式，提出基于核磁孔隙结构参数评价储层物性的评判标准.优质储层的主要标准如下：

(1)裂缝T2谱分布位置偏右、总幅度为高值；

(2)裂缝宽度均值较大；

(3)裂缝分选好，分选系数低，峰态值在1附近.

如图4，在Moux-21井3820.0～3829.0 m段具有较大裂缝宽度(谱分布靠右，裂缝宽度均值大)，且具有较强的谱幅度，说明裂缝发育较丰富，Cd路径图显示：路径具有明显的向上偏移特征.该井段强裂缝谱分布与计算渗透率均具有很好的对应性.

图4 Moux-21井球缝模型优化反演

3.2 孔隙结构参数与储层物性参数及生产数据的关系

将球缝模型优化反演得到的孔隙结构参数与岩心分析物性参数、目标层段的生产数据进行了对比分析，球缝模型计算的孔隙结构参数与岩石的物性实验分析数据以及储层的生产测试数据呈较好的相关性.

图5a是Moux-17井龙王庙组品质因子与球孔均值半径之间的关系.从数据整体分布趋势上可以发现，球孔均值半径增加，储层的品质因子迅速下降.但是，数据点分布缺乏规律性.究其原因，球孔半径增加，储层品质因子迅速下降的物理机制是：当球孔半径增加时，挤占了裂缝的发育空间，从而导致储层的渗流能力迅速下降.对图5a进行分析研究发现，数据点的分布呈两种不同程度的指数关系变化，分别对变化趋势相同的点再做图(图5b、图5c)进行分析，发现品质因子与球孔半径之间的关系非常清晰且相关性明显变好.

图5 Moux_17 井层段储层品质因子与球孔均值半径的相关分析

图5b是图5a矩形框内数据，可以拟合得到品质因子与球孔均值半径之间的关系式：

(12)

其中，Rsm为球形孔均值半径，μm；K为渗透率，mD；φ为孔隙度；R为相关系数.

图5c是图5a矩形框外数据，可以拟合得到品质因子与球孔均值半径之间的关系式：

(13)

尽管图5b和图5c得到不同的参数拟合关系，但反映趋势变化是一致的，即球形孔均值半径增加均导致品质因子降低.另外，图5b参数相关性很好，而图5c参数相关性很差，说明图5b和图5c数据点对应储层段的均质性存在差异，图5c储层岩石的孔隙空间具有更强的非均质性.图5b数据点分布规律性很好，说明对应储层岩石的孔隙和裂缝尺寸属于有规则的变化，即裂缝均值宽度与球形孔均值半径具有相同的变化方向，即同步增加或减小.图5c数据点相关性很差，说明对应层段球形孔均值半径与裂缝均值宽度在数值上的变化缺乏规律性，裂缝的空间排列可能是杂乱的.

分析研究品质因子与裂缝均值宽度、球形孔分选系数、裂缝分选系数之间的相关性，发现品质因子与这些孔隙结构参数之间的关联性均不明显.其主要的原因是，品质因子着重刻画储层的整体品质和渗流特征，基于球缝模型计算的孔隙结构参数，着重刻画储层的局部微观渗流孔隙和裂缝特征.如果储层物性整体具有比较明确的变化规律性，则品质因子与球缝模型的孔隙结构参数形成比较好的相关关系；如果储层具有非常强烈的非均质性，且孔隙、裂缝尺寸无规律变化，则品质因子与孔隙结构参数之间相关性变差，甚至完全没有关系.

在已经完成核磁优化反演的12口井中，研究对比孔隙结构参数与岩心实验分析数据、储层测试产量之间的关系，目的是验证孔隙结构参数对储层物性的刻画效果.图6给出了Moux_17井孔隙结构参数与岩心实验分析数据、储层流体测试产量之间的对比分析，该井剖面是白云岩，普遍具有比较强的储层物性非均匀性.裂缝发育段的岩心实验分析渗透率可达1.0 mD(1 mD=0.987×10-3μm2)左右，非裂缝发育段的岩心分析渗透率在0.05 mD左右，长弛豫时间的强振幅裂缝谱与岩心实验分析的高渗透率具有对应的关系，即优化反演的裂缝谱特征与岩心实验分析结果是对应的.在4609.0～4673.0 m深度段进行流体生产测试，产气39万方/天.该井段球缝模型优化反演的孔隙结构参数显示：在测试深度段，至少有三个井段出现了明显的长弛豫时间的强振幅裂缝谱，与其对应的Cd路径普遍向上偏移，两者都表明该井段存在较为丰富的大张开度裂缝发育带，故该井段测试获得较高气产量.

图6 孔隙结构参数与储层测试结果的对比分析(Moux-17井)

图7是Moux_204井球缝模型优化反演计算孔隙结构参数与测试层段的产量对比.该井在4655.0～4685.0 m深度段进行了产能测试，天然气产量为116万方/天.该井段优化反演的孔隙结构参数显示：在测试井段具有三段长弛豫时间的强振幅裂缝谱，表明存在丰富的大张开度裂缝发育带，因此该井段测试获得高产气量.

图7 孔隙结构参数与储层测试结果的对比分析(Moux-204井)

综上所述，球缝模型优化反演的孔隙结构参数与储层岩心的实验分析数据、储层的实际测试流体产能是一致的.

4 讨论与结论

本文建立了评价裂缝储层的球缝模型，并完成基于球缝模型的核磁回波优化反演算法，编写了该套优化反演算法的实用化核磁测井处理程序.对12口井核磁回波进行优化反演处理，得到裂缝储层的孔隙结构参数(包括球形孔均值半径、裂缝均值宽度、裂缝分选系数、峰态等).将核磁回波优化反演得到的孔隙结构参数与岩心分析的孔渗实验数据、储层测试产量数据分别进行了分析研究.结果发现，部分孔隙结构参数与岩心实验分析数据具有较好的相关性，裂缝谱分布特征与储层测试产能具有较好的相关性，并证实储层的渗流特征与裂缝发育程度有关.结论如下：

(1)分析研究孔隙结构参数与储层物性参数(品质因子)之间的关系，发现品质因子与球孔均值半径具有很好的负相关性.其负相关性与储层的均质性有关，均质性越好，负相关性越强.反之，如果储层存在非常强的非均质性，品质因子与球孔均值半径的相关性变差，甚至没有关系.

(2)长弛豫时间的强振幅裂缝谱与测试井段高产气量具有很好的对应关系.应用球缝模型优化反演结果能够很好地区分裂缝储层和致密层，并揭示裂缝储层的渗流能力与裂缝的发育程度密切相关.

(3)球缝模型优化反演算法的核心是确定Cd值的寻优方法，据Cd值分布位置可以定性判断储层中裂缝和孔隙的相对发育程度.