青藏高原及周边区域岩石圈重力势能及其产生的偏应力场

李忠亚， 胡敏章， 王勇， 汪健2,， 申重阳， 李辉

1 中国科学院精密测量科学与技术创新研究院， 大地测量与地球动力学国家重点实验室， 武汉 430077 2 中国科学院大学， 北京 100049 3 中国地震局地震研究所， 中国地震局地震大地测量重点实验室， 武汉 430071 4 引力与固体潮国家野外观测研究站， 武汉 430071 5 湖北省地震局， 武汉 430071

0 引言

印度和欧亚板块持续碰撞挤压，形成了大规模的青藏高原造山带.青藏高原是全球海拔最高的高原，平均高程4 km以上，被称为“世界屋脊”和“地球第三极”(高原及周边区域地形见图1).地震学和重力学研究表明，青藏高原内部地壳较厚，高原周边区域地壳较薄，且相同深度高原内外密度存在差异(滕吉文，1979；滕吉文等，1983；Molnar, 1988; 沈旭章等，2013；李红蕾等，2017；Shen et al., 2016; Tian et al., 2021).当岩石圈质量存在横向差异时，重力作用会驱使大质量块向小质量块运动，从而影响地表地形和密度结构横向分布不均匀的岩石圈的构造应力场和构造变形(Artyushkov, 1973; Fleitout and Froidevoux, 1982, 1983; Coblentz et al., 1994; Sandiford and Coblentz, 1994; Iaffaldano et al., 2006).因此，青藏高原及周边地区岩石圈显著的横向密度和地表地形变化是产生其构造应力场及形变不可忽视的力源(Jones et al., 1996; Flesch et al., 2001).

图1 青藏高原及周边区域地形，黑线为二级活动地块边界，红线表示喜马拉雅主推覆断裂，蓝色箭头表示水平GNSS速度(Zheng et al., 2017)

单位面积岩石圈柱体重力势能为单位面积质量和其相对参考深度(一般取岩石圈厚度)的高度的乘积沿整个岩石圈积分(Jones et al., 1996)，其大小与岩石圈质量分布和参考位置有关.岩石圈重力势能差即为相邻柱体间因岩石圈地表地形和密度横向变化而引起的重力势能之差.岩石圈重力势能可以根据大地水准面高数据和岩石圈密度结构数据计算.Turcotte和Schubert(1982)推导了重力势能差和大地水准面高之间简单解析公式，该公式在完全均衡条件下成立，且计算结果与大地水准面的滤波方法关系密切(Ghosh et al., 2009).Coblentz 等(1994)给出了不同岩石圈类型的重力势能解析计算公式，后来随着多个地壳模型发布，现在最常用的方法是根据重力势能定义采用密度结构数据计算.现有关于青藏高原及周边区域重力势能计算研究，大多采用Crust 2.0地壳模型和EGM96地球重力场模型(Flesch et al.，2001; Ghosh et al., 2006, 2009, 2013)，且很多研究是从全球尺度来讨论，我们十分必要采用相对较新的Crust 1.0地壳模型和EGM2008地球重力场模型来研究青藏高原及周缘重力势能分布规律.

在地表地形和岩石圈密度结构横向分布不均匀引起的构造应力场计算方面，薄板模型是处理地球重力场与构造应力场之间关系的常用模型，其基本内涵是当岩石圈横向尺度远大于垂向尺度时，可将岩石圈近似为薄板.国际上许多学者是通过求解薄板模型下重力势能和偏应力之间平衡方程来研究重力场和构造应力场之间的关系(Flesch et al., 2000, 2001, 2007; Ghosh et al., 2006, 2009; Jay et al., 2017)，尽管该方法计算量大，求解复杂，然而其平衡方程求解巧妙，不需要流变信息作为先验信息，理论公式严密，这些使得该方法成为处理地球重力场与构造应力场问题的常用方法.国内学者提出了采用重力异常数据(如布格异常)直接计算不同深度构造应力的方法(游永雄，1994；向文和李辉，1999；郭飞霄等，2015；毛经伦等，2019；Xu et al., 2020)，但该方法采用了过多假设近似，大大限制了其应用范围.

精密的现代大地测量技术(如GNSS技术)是研究地壳构造变形的有效手段.Wang等(2001)采用中国大陆GPS观测数据，首次给出青藏高原及周边构造形变特征.随着GNSS技术的发展、相关观测网的布设、测站陆续增多和观测数据不断累积，许多关于青藏高原及其周边构造形变研究成果相继发表(Gan et al., 2007; Liang et al., 2013; Zheng et al., 2017; Jin et al., 2019; Zhang et al., 2019)，丰富的GNSS观测资料和研究成果为构建青藏高原及邻区现今应变场提供了坚实基础.构造大地测量学研究结果表明，岩石圈重力势能差和板块边界作用力是青藏高原构造形变作用力的重要来源(Flesch et al., 2000, 2001; Thatcher, 2009).但已有研究没有定量分析重力势能差产生的构造应力场和现今GNSS应变场之间的关系，因此本文将探讨重力势能差对青藏高原及周缘构造形变的贡献，以便深入认识该区域构造变形方式.

本文基于Crust 1.0地壳模型数据，并在其基础上通过均衡调整机制约束地幔密度，计算青藏高原及邻区重力势能.以研究区域平均重力势能作为参考构造状态重力势能，构建重力势能差模型.利用有限元方法求解重力势能差产生的偏应力场.接着，讨论地球重力场和构造应力场之间关系，并直接利用EGM2008地球重力场模型构建重力势能差及其产生的偏应力场.最后，根据青藏高原及周边GNSS速度场数据计算应变场，分析现今GNSS应变和重力势能差产生的偏应力场之间相关性，探讨重力势能差对青藏高原及邻区构造形变的贡献.本文的研究结果对深入理解青藏高原及周边地区的大地构造动力学和构造形变机制等具有参考意义.

1 方法

应力和重力之间平衡方程为

(1)

式中ρ为密度，σij为应力张量的ij分量(符号为正表示张裂)，gi为重力加速度第i分量，式中采用爱因斯坦求和约记.σij可以表示为

σij=τij+1/3(σxx+σyy+σzz)δij,

(2)

式中τij为偏应力张量的ij分量，δij为Kronecker符号.

当岩石圈横向尺寸远大于其垂向尺寸时，可将岩石圈抽象成薄板(Jones et al., 1996; 许才军和尹智，2014).采用薄板模型研究岩石圈密度结构和地表地形横向不均匀对构造应力场影响时，可通过求解平衡方程研究整个薄板垂向平均偏应力场(Flesch et al., 2000, 2001).为此，将式(2)代入式(1)并将各物理量从地表积分至参考深度L，取参考深度的平均值，有

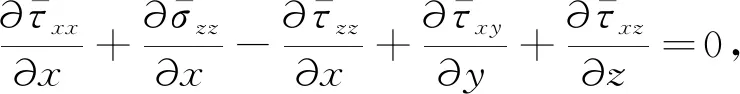
(3)

(4)

(5)

(6)

(7)

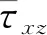
(8)

(9)

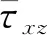
(10)

(11)

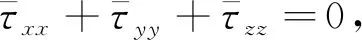
2 数据与计算结果

2.1 数据

研究重力势能横向变化对岩石圈构造应力场的影响需要地表地形数据和岩石圈密度结构数据.本文采用Crust 1.0地壳模型(Laske et al., 2013)数据计算岩石圈重力势能.Crust 1.0地壳模型分辨率为1°×1°，将全球划分为64800个网格，每个网格将地壳分成8层，即水层、冰层、上沉积层、中沉积层、下沉积层、上结晶地壳层、中结晶地壳层和下结晶地壳层.模型提供各层的边界数据和密度数据，同时提供莫霍面以下地幔密度，本文中将该数据作为地幔初始参考值.为了与Crust 1.0模型分辨率一致，本文地表地形数据采用该模型提供的第一层上边界数据.

2.2 未补偿重力势能计算结果

重力势能计算时，岩石圈参考深度L选为100 km(England and Molnar, 1997; Flesch et al., 2001; Ghosh et al., 2006)，在Crust 1.0地壳模型每层内部，密度为常数.莫霍面至参考深度间的地幔部分，其密度仍然采用Crust 1.0模型提供的参考数据.我们根据Crust 1.0地壳模型数据，首先积分计算全球每个格网中心点的重力势能，其余点重力势能通过格网中心点样条插值得到.直接根据Crust 1.0地壳模型数据计算得到的岩石圈重力势能分布见图2，由于该重力势能计算过程中未对Crust 1.0地壳模型提供的地幔参考密度进行改正，称该计算结果为未补偿模型.图2显示，青藏高原及周边区域重力势能总体分布极其不均匀，高重力势能几乎全部集中在青藏高原内部，青藏高原周边区域重力势能相对较低，并且在青藏高原边界附近出现高-低重力势能变化梯度带.重力势能分布特征还呈现与地形正相关特性，即地形高区域重力势能大，反之则为低重力势能分布.研究区域内高重力势能分布主要集中在柴达木—陇西块体和巴颜喀拉块体西部，最大重力势能达到了1579.99 MPa，在拉萨块体西南部和柴达木—陇西块体东部出现次高重力势能分布，但在柴达木盆地、羌塘块体东部和川滇块体南部出现了青藏高原内部相对低重力势能分布.上述分布使青藏高原内部呈现了以高重力势能分布为主、高低重力势能相间的特征，但就青藏高原内部总体分布而言，大致为由西向东重力势能逐渐减少.在塔里木块体、阿拉善块体、鄂尔多斯块体西部、华南块体西北部和印度板块等青藏高原周边区域重力势能较低，最低重力势能位于印度板块内喜马拉雅主断裂西部，其数值为1420.24 MPa.

2.3 考虑均衡补偿的重力势能计算结果

本节将讨论采用均衡补偿机制对Crust 1.0地壳模型提供的地幔初始参考密度数据进行约束改正.常见均衡调整机制有两种方式，即艾里均衡补偿模式和普拉特均衡补偿模式.前者调整方式是海平面以上地形部分盈余质量(或海平面以下亏损质量)以山根(或反山根)形式补偿；普拉特模式则是假设补偿面地形没有起伏，通过改变柱体密度进行均衡补偿.我们在图2未补偿重力势能的基础上分别计算艾里均衡调整和普拉特均衡调整补偿后的重力势能.

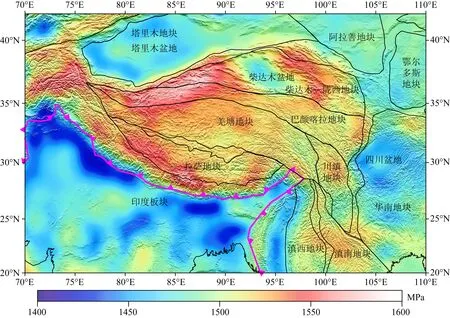
图2 青藏高原及周边区域未补偿重力势能

计算考虑艾里均衡补偿的重力势能，国际上有两种策略：(1)Flesch等(Flesch et al., 2000, 2007; Flesch and Kreemer, 2010)和Jay等(2017)研究青藏高原、北美西部和智利中部重力势能分布时，艾里均衡补偿对重力势能的影响是通过山根或反山根方式计算；(2)Ghosh等(2009)和Neves等(2014)计算艾里均衡补偿的重力势能时，在地表地形中扣除动力地形部分贡献，该方法的不足是容易混淆均衡补偿和岩石圈下部密度差作用(Naliboff et al., 2012).我们计算艾里均衡补偿的重力势能模型时，采用前者，即青藏高原及周缘地形部分盈余质量通过地壳底部插入地幔部分的山根进行补偿，山根的深度采用Crust 1.0地壳模型提供的地形数据、上沉积层密度、下结晶地壳密度和地幔密度等数据计算.计算重力势能时山根的密度采用艾里均衡补偿后的数据，其余数据仍采用Crust 1.0地壳模型结果，由此计算的重力势能分布见图3，我们称该结果为艾里均衡补偿重力势能模型.与图2中未补偿重力势能模型相比，图3重力势能数值稍许减小，其变化区间为1413.22～1533.80 MPa，平均重力势能为1476.04 MPa.艾里均衡补偿的基本观点是海平面以上质量被其下面低密度物质所补偿，因此重力势能计算中加上艾里均衡补偿后数值必然降低.但是，考虑艾里均衡调整后，重力势能整体分布规律并未改变，仍然是青藏高原内部为高重力势能分布区，周边区域重力势能较低.

计算考虑普拉特均衡补偿的重力势能时，我们的计算方法是将海平面以上的盈余质量(或海平面以下亏损质量)通过调整地壳底部至参考深度L间的地幔密度来补偿，然后采用均衡调整后的地幔密度计算重力势能，计算结果见图4，我们称该结果为普拉特均衡补偿重力势能模型.与未补偿重力势能模型相比，普拉特均衡补偿模型重力势能分布特征与其基本一致，但补偿后重力势能数值略微下降，其平均值为1481.50 MPa，变化区间为1415.00～1552.15 MPa，造成该种变化的原因是普拉特均衡调整机制通过地壳底部至参考深度间低密度补偿海平面以上盈余质量，因此会导致重力势能数值比未补偿模型小.比较图3和图4可以发现，两种均衡调整补偿后重力势能分布特征基本一致，但是艾里均衡补偿对于重力势能数值影响更大.

2.4 青藏高原重力势能差产生的偏应力场

求解重力势能横向变化产生的偏应力场，首先需要计算重力势能差，即重力势能与构造参考状态重力势能之差(Flesch et al.,2000,2001; Ghosh et al., 2009).构造参考状态重力势能可采用研究区域重力势能模型的平均值(Coblentz et al., 1994)，将重力势能模型数值减去构造参考状态重力势能即得重力势能差.根据前面构建的三种重力势能模型(图2、图3和图4)分别计算，得到重力势能差，采用FEMCalculation程序(李忠亚，2017)计算了对应的重力势能差产生的偏应力场(图5).未补偿重力势能差产生的偏应力(图5a)分布特征整体表现为地形高的青藏高原内部为张裂应力，青藏高原周边的低地形区域(如塔里木盆地、四川盆地和印度板块北部)则是压缩应力.青藏高原及周缘偏应力数值主要集中在10～30 MPa区间内，最大主张应力方向在青藏高原西部为NNE-SSW，青藏高原中部(拉萨块体中北部与羌塘块体中部和巴颜喀拉块体中部)几乎接近N-S分布，而在青藏高原东部则较复杂，具体表现为东北部由高原中部接近N-S样式逐渐过渡为NNE-SSW，川滇块体、滇南块体北部和滇西块体北部接近E-W方向，在滇南块体南部主要表现为NEE-SWW.在塔里木盆地，重力势能差产生的最大主压应力方向由盆地东边NNE-SSW转变至盆地西边的NNW-SSE，四川盆地最大主压应力方向为NWW-SEE.印度板块东北部至西北部，最大主压应力方向由近N-S 逐渐过渡至NW-SE.将艾里均衡补偿和普拉特均衡补偿两种重力势能差产生的偏应力场(图5b 和5c)与未补偿重力势能差得到的偏应力场比较可知，三种偏应力场分布样式几乎一致，但是经均衡调整改正的偏应力场应力数值变小，艾里均衡补偿和普拉特均衡补偿两种偏应力场模型的最大偏应力数值大小分别是25.96 MPa和25.30 MPa.与未补偿重力势能模型相比，均衡调整使重力势能数值变小并降低重力势能水平变化幅度，最终导致均衡补偿模型求解的偏应力比未补偿模型结果减小.

图3 青藏高原及周边区域艾里均衡补偿后的重力势能

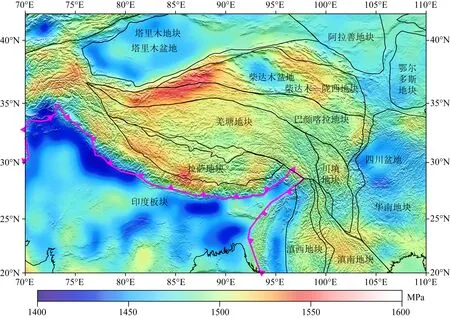
图4 青藏高原及周边区域普拉特均衡补偿后的重力势能

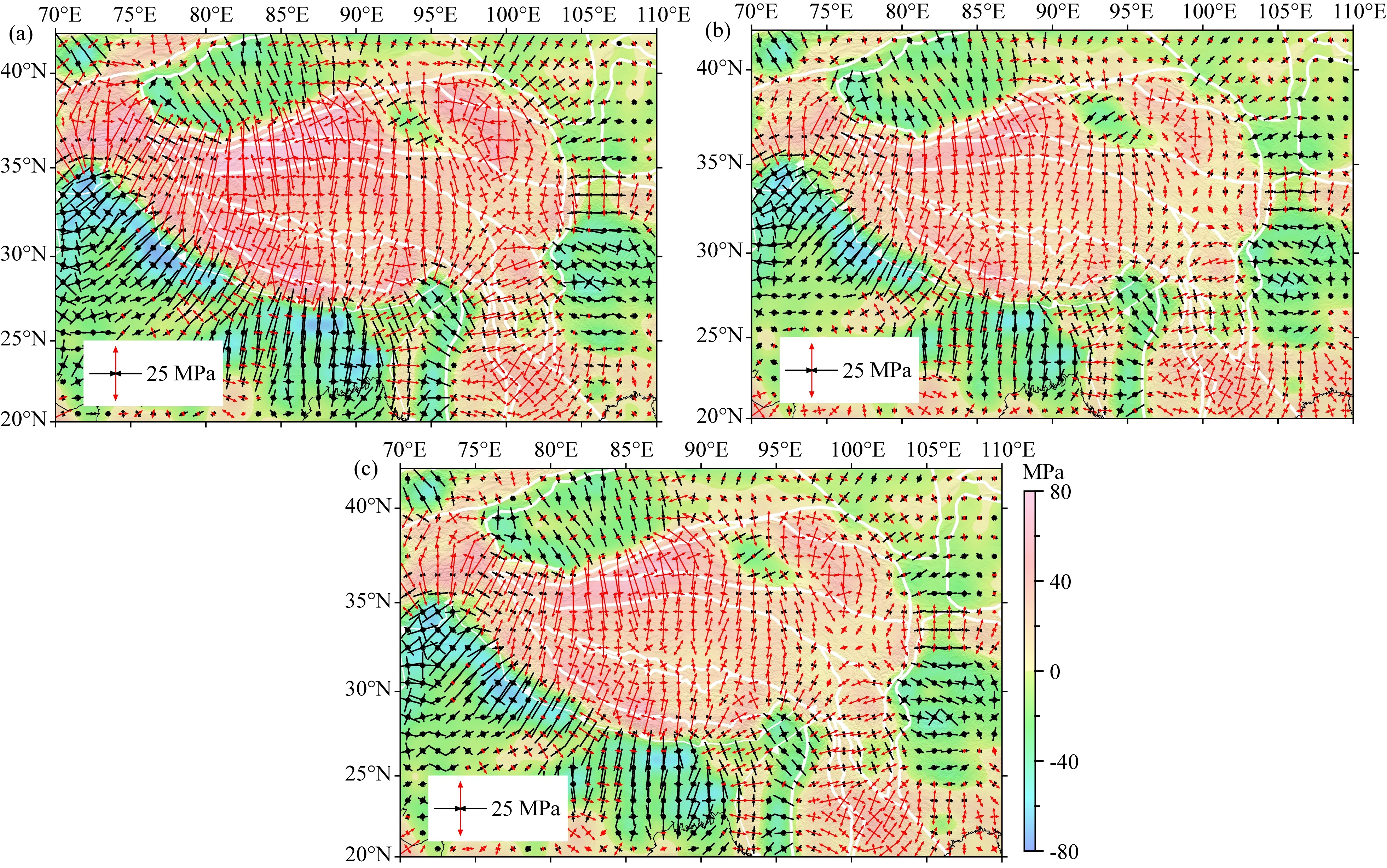
图5 青藏高原及周边区域重力势能差产生的偏应力

3 讨论

3.1 地球重力场和构造应力场之间关系

地球重力是由地球对物体的引力和地球自转产生的离心力的合力，空间域中每一点均有惟一的重力与之对应，即地球重力场.地球重力场反映了地球系统中物质的分布和运动状态，包括地球内部质量、密度的分布和变化和地球物质空间分布、运动和变化.构造应力场表示一定范围内某一瞬时的应力状态(徐开礼和朱志澄，1989)，其时空变化是导致地壳形变、破裂、褶皱等地质现象的直接动因(姚瑞等，2017).地球重力场和岩石圈构造应力场之间联系是：岩石圈密度结构和地表地形横向不均匀，在地球重力场作用下可以产生横向作用力形成构造应力，这种横向作用力在薄板模型下可以用重力势能差定量描述(Turcotte and Schubert, 1982; Jones et al., 1996; Flesch et al., 2000, 2001; Ghosh et al., 2009).国内在20世纪90年代，游永雄(1994)给出了由布格重力异常计算构造应力场的方法.此后，向文和李辉(1999)和Xu等(2020)对该方法进行了发展，但核心思路依然是采用重力异常(如均衡异常)计算构造应力；郭飞霄等(2015)和毛经伦等(2019)采用该方法计算了川西地区水平构造应力场.然而，该方法数理模型不够严谨，具体表现为：用矢量来表示不同深度水平构造应力；将重力水平矢量方向来近似代替构造应力最大主方向，无法表示压缩应力和张裂应力；采用布格重力或均衡重力异常无法考虑地表地形横向差异对构造应力场的贡献.许才军和尹智(2014)对国内外利用重力数据计算构造应力场的研究进展进行了综述，建议构建弹性、黏弹性和弹塑性的利用重力数据计算地壳构造应力应变场的解析模型.本文第1节中阐述了地球重力场和构造应力场之间理论关系，该方法从重力与应力平衡方程出发，基于薄板模型，建立了偏应力和重力势能之间的平衡方程，并在偏应力第二不变量最小约束下求解平衡方程，得到偏应力场，该方法是研究地球重力场和构造应力场之间关系的严密方法.

重力势能差可以采用大地水准面高估算，从而可由重力场模型通过求解第1节的平衡方程得到偏应力场.下面将利用EGM2008地球重力场模型计算青藏高原及周边区域重力势能差及其产生的偏应力场，并将计算结果与第3节中Crutst 1.0 地壳模型结果进行比较.大地水准面高ΔN和重力势能差ΔU之间关系(Sandiford and Coblentz, 1994)为

(12)

式中，g为重力加速度，G为万有引力常数.为与第1节中定义的重力势能一致，通过式(12)计算的重力势能差需要除以岩石圈参考深度100 km.由于Crust 1.0地壳模型分辨率为1°×1°，因此我们将EGM2008地球重力场模型的最大阶次数截取至200.重力场模型低阶次项包含岩石圈下面地球物质对大地水准面的影响，需要扣除其贡献，但两者之间没有一一具体对应关系.Ghosh等(2009)计算全球重力势能差时减去7阶次以下系数，Neves等(2014)研究伊比利亚地区重力势能差时是去除12阶次以下系数.本文将待去除的阶次系数设置在区间[5,15]，然后逐一试算.以高地形重力势能差为正、低地形为负作为筛选条件，最终确定去除10阶次以下系数.采用上述策略，由大地水准面高计算的重力势能差及其产生的偏应力场见图6.青藏高原南部为高重力势能差分布区域，最大重力势能差达到了45.367 MPa，塔里木盆地、柴达木盆地、四川盆地和印度板块北部均为低重力势能差区域.青藏高原内部正重力势能差产生张裂应力，负重力势能差则是压缩应力，应力大小主要分布在1～20 MPa.

对比图5和图6可知，整体上EGM2008地球重力场模型计算的重力势能差与Crust 1.0地壳模型结果较相似，即青藏高原内部除柴达木盆地外均为正重力势能差，青藏高原周边大部分区域重力势能差小于青藏高原内部.但是，两者具体细节分布规律存在较大差异，如EGM2008 地球重力场模型结果最大重力势能差主要分布在青藏高原南端，并向北递减，而Crust 1.0模型在青藏高原西北部和东北部均存在高重力势能差分布.两种模型结果重力势能差分布差异导致偏应力分布存在相应的区别.造成两者细节差异较大的主要原因是，式(12)仅在满足完全均衡条件下才成立(Turcotte and Schubert, 1982; Ghosh et al., 2009)，实测重力结果显示青藏高原并非处于完全均衡状态(张永谦等，2010；陈石等，2011；付广裕等，2015).此外，重力场模型系数的选取对结果有一定影响，但难以在球谐系数中完全分离出岩石圈物质.综上，式(12)表示的方法使用时前提条件较苛刻且对重力场系数选取存在难度，因此该方法只能作为重力势能差的一种近似估算方法.但该方法可直接得到重力势能差，在实际计算中可作为一种独立方法，用于与其他结果比较.

图6 利用EGM2008地球重力场模型计算的青藏高原及邻区重力势能差(a)及其产生的偏应力(b)

3.2 重力势能差产生的偏应力与GNSS现今构造形变

现代空间大地测量观测技术(如GNSS技术)能够精确测量板块之间相对运动，其观测结果可揭示板块之间和板块内部的构造变形方式.我们收集Zheng等(2017)和Kreemer等(2014)发表的青藏高原及其周边共计2576个测站GNSS速度场资料(图1)，利用Shen等(1996)提出的应变计算方法，采用SSPX程序(Cardozo and Allmendinger, 2009)计算了青藏高原及周缘现今应变场.计算结果(图7)表明，青藏高原及其周边区域GNSS现今构造应变场和该地区长期地质构造背景相符合.在喜马拉雅和龙门山等地区以压缩应变率为优势分布，与这些造山带的地壳压缩变形一致；青藏高原内部羌塘块体中南部和拉萨块体中北部存在近东西向张裂应变，与这些区域发育的正断层分布一致；青藏高原周边的华南块体和塔里木块体作为稳定的构造单元，其应变明显小于青藏高原内部.

图7 青藏高原及周边区域GNSS主应变率

青藏高原及周边区域GNSS应变场较好地反映了该地区现今构造形变.为了分析重力势能作为一种构造运动驱动力对于岩石圈构造形变的贡献，我们将重力势能差产生的偏应力场和GNSS应变场进行比较.偏应力场与应变场之间的相关程度可以采用Flesch等(2007)定义的相关系数C来描述，相关系数公式为

(13)

E和T分别表示应变和偏应力第二不变量，ε为GNSS应变张量.相关系数C数值变化范围为[-1,1].相关系数等于1，表示偏应力场和应变场完全匹配，即偏应力场与应变场的压缩张裂样式、偏应力张量与应变张量相对数值大小和主轴方向一致；若相关系数等于-1，则表明偏应力场与应变场负相关；若相关系数为0，则表示偏应力场与应变场不相关.我们分别计算了未补偿、艾里均衡和普拉特均衡三种重力势能差模型产生的偏应力场(图5(a、b、c))与GNSS应变场之间相关系数(图8).三种相关系数模型结果没有显著差别，这主要是因为均衡调整改正均未根本改变重力势能分布规律，进而相应的偏应力场和相关系数均会十分接近.在青藏高原内部，柴达木盆地和川滇块体中南部，重力势能差产生的偏应力场和GNSS应变场呈高相关性，高原内部其余区域两者相关性则较弱，甚至在柴达木—陇西块体东部和拉萨块体南部还呈现负相关特性.青藏高原周缘，如塔里木块体西北部、阿拉善块体南部、鄂尔多斯块体西部、华南块体西北部和喜马拉雅主断裂以南区域的中部和西部，重力势能差产生的偏应力场和GNSS应变场展现较强相关性.偏应力场和应变场之间的相关性主要与两者的压缩张裂样式和主轴方向有关，对比重力势能差产生的偏应力场和GNSS应变场，在相关性强的区域，两者的压缩张裂样式和主轴方向均符合较好.相关性弱甚至负相关区域，如柴达木-陇西块体东部和拉萨块体南部，偏应力分布样式以张裂为主，而应变场最大主方向样式则是压缩.

图8 青藏高原及周缘重力势能差产生的偏应力和GNSS应变之间相关系数

重力势能差产生的偏应力场和GNSS应变场之间相关性强，表明重力势能差对构造形变贡献大，若两者相关性弱则表示构造变形受其他构造驱动力源(如地幔对流产生的牵引力和边界载荷作用等因素)所控制.大量研究结果(张健和石耀霖, 2002; England and Molnar, 1997; Flesch et al., 2001; Ghosh et al., 2006; Ghosh and Holt, 2012; Schmalholz et al., 2014, 2019)指出，重力势能差是青藏高原构造变形必不可少的构造力源.我们研究结果进一步表明，在重力势能数值较大的区域，如青藏高原中西部和东北部，重力势能差对构造形变贡献微乎其微，只有在重力势能横向梯度变化剧烈的区域，如柴达木盆地、川滇块体中南部和青藏高原周缘，重力势能差对构造形变的影响才是不可或缺.

青藏高原周缘的塔里木块体西北部，阿拉善块体南部，鄂尔多斯块体西部、华南块体西北部和青藏高原内部川滇块体中南部，重力势能差产生的偏应力和GNSS应变相关性强，板块运动驱动力在远离欧亚板块边界区域以重力势能的形式影响其构造形变.上述青藏高原周缘区域构造形变较小，而高原内部川滇块体中南部却较大，这与两者岩石圈流变性质有关，前者黏度大，而后者黏度小(石耀霖和曹建玲，2008; Flesch et al., 2001; Jay et al., 2017)，故导致形变差异.喜马拉雅主断裂南端，尽管重力势能差产生的偏应力和GNSS应变相关性强，但是该区域重力势能差产生的压缩应力是北部青藏高原内部高重力势能压缩南部低重力势能的结果，而GNSS压缩应变则是南部印度板块向北部高原俯冲的结果，两种机制作用力方向完全相反.

关于青藏高原构造形变的动力学机制存在不同观点.England和Molnar(1997)认为青藏高原形变遵循重力势能差和应力之间平衡方程，Flesch等(2001, 2007)联合重力势能差和板块边界作用力两种力源解释欧亚碰撞带的动力学过程，Ghosh等(Ghosh et al., 2008；Ghosh and Holt, 2012)则认为重力势能差和地幔对流联合作用控制青藏高原动力学过程.本文上述关于重力势能差产生的偏应力场和现今GNSS应变场之间相关性分析表明，重力势能差在青藏高原及邻区不同区域对形变影响不同.在喜马拉雅地区，印度板块可以克服重力势能差的影响持续俯冲，这表明印度板块驱动力的影响比重力势能差更大.因此，青藏高原构造形变的动力来源至少包含重力势能差和印度板块驱动力.

4 结论

本文基于Crust 1.0地壳模型计算了青藏高原及周边区域重力势能，并根据重力势能差求解了其产生的偏应力场.在此基础上讨论了地球重力场和构造应力场之间关系和重力势能差对青藏高原及周缘构造形变的影响，得出的主要结论如下：

(1)本文以Crust 1.0地壳模型作为青藏高原及周边区域重力势能计算的基本参考模型，在此基础上分别采用艾里均衡和普拉特均衡两种方式对地幔密度进行约束，由此构建青藏高原及周边区域重力势能分布模型.未补偿、艾里均衡补偿与普拉特均衡补偿三种方式计算的重力势能变化范围分别为1420.24～1579.99 MPa，1413.22～1533.80 MPa和1415.00～1552.15 MPa.重力势能与地形呈正相关关系，青藏高原内部重力势能普遍较高，高原四周则为低重力势能分布.高原西北和西南区域为高重力势能聚集区，印度板块北部、塔里木盆地、四川盆地和柴达木盆地是主要低重力势能区域.高原边界重力势能分布表现为正负急剧变化梯度带特征.

(2)以研究区域平均重力势能为构造参考状态重力势能，计算青藏高原及周边区域重力势能差分布，然后求解其产生的偏应力场.地形高的青藏高原内部重力势能差为正，产生偏应力以张裂样式为优势分布；地形低的青藏高原周边重力势能差为负，偏应力以压缩为主要分布特征.青藏高原及周边区域重力势能差产生的偏应力大小主要分布在10～30 MPa.

(3)地表地形和岩石圈密度结构存在横向差异时，在地球重力场作用下可以产生横向构造应力.求解重力势能与偏应力之间平衡方程是研究地球重力场和构造应力场之间关系的有效方法.大地水准面高和重力势能差之间具有简单关系，但其仅在均衡区域才成立，该关系可作为研究重力势能差的独立近似方法.

(4)重力势能横向变化剧烈区域，重力势能差对于构造形变贡献突出.青藏高原内部的柴达木盆地和川滇块体中南部，以及青藏高原周缘的塔里木块体西北部、阿拉善块体南部、鄂尔多斯块体西部、华南块体西北部和喜马拉雅主断裂以南区域的中部和西部，这些地区重力势能差产生的偏应力场和GNSS应变场相关性强，重力势能差对构造形变的影响大.在远离欧亚板块边界的青藏高原北部和东部边缘，板块运动驱动力以重力势能的形式影响构造形变，而在喜马拉雅地区，重力势能差与印度板块俯冲两种机制作用方向相反.

致谢感谢两位匿名审稿专家提出的宝贵意见和Ghosh Attreyee博士、Stamps D. Sarah博士和张倩文同学的有益讨论.