固体物理教学中电子态密度的计算

杜 林，田宏玉，任重丹

(1. 临沂大学 物理与电子工程学院，山东 临沂 276005；2. 遵义师范学院 物理与电子科学学院，贵州 遵义 563006)

在固体物理学和统计力学中，态密度(density of states或简化为DOS)是一个很常见且非常重要的概念.由N个相同原子组成的晶体中，每个原子轨道会形成N个能级.每个能级可以容纳2个不同自旋的电子，从而一共有2N个电子状态.由于N是个很大的数，这些分离的电子状态排列是异常密集的，呈准连续分布，这导致具体讨论单个能级是没有意义的.电子的状态密度可以帮助我们了解晶体中电子态的分布状况.电子的状态密度或态密度为某一能量附近每单位能量区间里的微观状态数目，又叫做能态密度，通常用g、ρ、n或N表示.能量在E～E+ΔE区间的电子能态数可表示为ΔZ=N(E)·ΔE.实验上，费米面附近的电子态密度可以通过光电子能谱、扫描隧道显微镜或电子能量损失谱等方法测量.

由于教学的需要，在常见的教材中[1-5]对电子态密度的计算只涉及简单的模型，如色散关系具有球对称性的自由电子气.而与实际晶体相关的近自由电子情形只给出了计算结果，并没有具体的计算步骤，因此学生很难对常见的晶格结构进行态密度计算.本文将详细介绍如何采用教材中的公式对石墨烯和面心立方晶格的态密度进行计算，从而得到态密度随能量的变化规律以及态密度导数不连续的范霍夫奇点.

1 电子能态密度的计算公式

一般地,在N个电子能级系统中，态密度的定义为

(1)

其中2源于每个能级可以容纳两个不同自旋的电子.考虑到电子能级的准连续性，求和可以转换为积分形式：

(2)

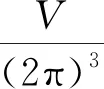
(3)

其中等式右侧指dσ(x)沿g-1(0)的d维曲面积分，三维晶格的电子态密度可以写成曲面积分的形式：

(4)

这是大部分固体物理教材中给出的态密度计算公式，其中dS的积分区域是在第一布里渊区内的等能面S(E)，E(k)是等能面的梯度，其方向垂直于等能面.积分类型为第一类曲面积分，即标量场的曲面积分.由于E(k)在倒空间中是波矢k的周期函数，在布里渊区某些高对称点上E(k)=0，从而导致态密度的一阶导数不连续，这些发散点即是范霍夫奇点.

类似地，二维晶格态密度的一般表达式为

(5)

其中S是二维晶体的面积，dl的积分区域是第一布里渊区内的等能曲线l(E).

2 二维石墨烯的态密度

根据轨道杂化理论，石黑烯的2s轨道和2p轨道形成3个sp2杂化轨道.在紧束缚近似下，二维石黑烯的色散关系为

(6)

其中ε=εsp+J0，εsp是原子的sp2杂化轨道能量，J0是完全重叠积分，J是最近邻重叠积分.根据色散关系可得能量在等能面上的梯度：

(7)

其中已设石墨烯的基矢长度a=1.为了计算电子的态密度，需要在等能曲线上进行积分.等能曲线可以采用下面的方法求得：给定某能量值，让kx遍历整个布里渊区寻找有意义的ky值：

(8)

即ky需要满足条件：-1≤cos(ky/2)≤1.然后把积分元dl投影到x轴，得到

(9)

从而公式(5)求态密度的第一类曲线积分简化为对kx的定积分，积分可以用黎曼和实现.同时kx和ky要限定在第一布里渊区，即

(10)

在进行数值计算时，kx的取值可以通过循环语句实现,kx和ky限定在第一布里渊区可通过判断语句来控制.计算结果如图1所示.

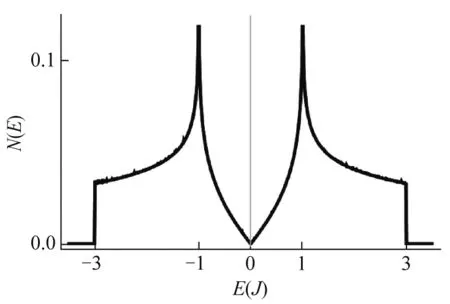
图1 石墨烯的态密度，其中设ε=0，J=1

其中E=0对应着布里渊区的狄拉克点(K和K′)，可看出态密度关于狄拉克点是对称的，这是由于能谱的粒子空穴对称性；此外态密度的导数在E=±1和E=±3处不连续，这分别对应石黑烯布里渊区的两个高对称点M和Γ.

3 面心立方晶格的s带能态密度

面心立方是一种常见的三维晶格结构，很多元素晶体都属于面心立方结构，如金、银、铜等.面心立方晶格s带能带态密度的计算步骤和石墨烯类似，唯一的区别是二维石墨烯的等能区域是曲线，面心立方晶格的等能区域是曲面.在紧束缚近似下，面心立方晶格s态电子能带表达式为

(11)

其中ε=εs+J0，εs为原子的s能级，J0是完全重叠积分，J是最近邻重叠积分，a是面心立方晶格的单胞基矢长度.从E(k)函数关系式可知能量在等能面上的变化率为

(12)

类似地，为了计算s带的态密度,需要在等能面上进行曲面积分.让kx和ky遍历整个布里渊区寻找有意义的kz值即可确定等能面，有

(13)

即kz要满足-1≤cos(kza/2)≤1.根据公式(4)把积分元曲面dS投影到xy平面上,即

(14)

从而公式(4)求态密度的第一类曲面积分化简为对(kx,ky)的二重积分，积分可以通过黎曼和实现.写出面心立方第一布里渊区截角八面体的平面方程后，通过判断语句可把kx、ky、kz限定在第一布里渊区内[9].面心立方晶格态密度的计算如果如图2所示.

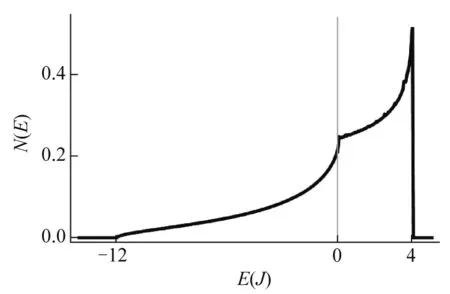
图2 面心立方s带的态密度，其中设ε=0，t=1

可以看出态密度的导数在E=-12、0、4处不连续，这分别对应着面心立方布里渊区Γ、L、M三个高对称点，其中Г处于能带底，Μ处于能带顶.类似地，简单立方、体心立方、六角密排等三维晶格结构的态密度也可以通过上述步骤求得.

4 结论

利用教材中态密度公式本文计算了石墨烯和面心立方晶格的态密度.计算过程凸显了如何把公式程序化，从而进行数值运算.计算思路也有助于学生对其它晶格结构的电子态密度以及声子态密度进行计算.