结合模糊聚类的多示例集成算法

韩海韵，杨有龙，孙丽芹

西安电子科技大学 数学与统计学院，西安 710126

1997年，Dietterich等人[1]在研究分子活性问题时发现：同一种分子在不同的条件下有不同的低能形状，专家只知道该分子具有活性，但不知道是哪一种低能形状对分子的活性起作用。若将有活性分子的全部低能形状都作为正示例，无活性分子的全部低能形状作为负示例，然后用传统监督分类器训练，在预测阶段，会导致很高的假阳性率，为此，Dietterich等人[1]提出了多示例学习。在多示例学习框架下，训练对象是包，一个包中有多个示例，包的标签是已知的，包中示例的标签是未知的，多示例学习的目标是对未知包进行标记。标准多示例假设规定：正包中至少有一个正示例，负包中全部都是负示例。在分子活性预测问题中，分子由包表示，分子的低能形状由示例表示，活性分子对应包的标签为正，无活性分子对应包的标签为负。多示例学习现已应用于更加广泛的领域，如图像分类、文本分类、目标识别、股票预测等。

目前，主要有三类多示例方法：示例空间的方法、包空间的方法、嵌入空间的方法。示例空间的方法认为具有区分度的信息存在于示例之间，训练示例级的分类器，如APR[1]、Diverse Density[2]、mi-SVM[3]、RSIS[4]等；包空间的方法认为具有区分度的信息存在于包之间，把包视为一个整体，定义包之间的距离和相似性，训练包级的分类器，如Citation-KNN[5]、CCE[6]、MinD[7]、BoW[8]等；嵌入空间的方法基于一组示例原型，将包映射到嵌入空间，在嵌入空间中，包由一个特征向量表示，然后用传统的监督算法学习分类器，如MILES[9]、MILIS[10]、MILDM[11]、MILMPC[12]等。

目前许多多示例方法都对数据隐式地做出了假设：（1）正包中正示例的比例；（2）示例的分布。APR算法学习一个超矩形区域，正包中至少有一个示例在该超矩形内，负包中所有示例都不在该矩形内；DD算法学习一个概念点，正包中至少有一个示例离该点很近，负包中所有示例都远离该点，APR和DD都对正示例的分布做出了隐含假设：正示例来自一个紧凑的簇。因此，它们只在单模态分布的数据上效果较好，不适用于多模态分布的数据。Simple-MI[13-14]将包映射为最小最大向量，mi-SVM和MI-SVM[3]的初始阶段，将包表示为其所包含示例的算数平均值，它们都假设了正包中全部都是正示例。SVR-SVM[15]和r-rule[16]估计了正包中正示例的比例，假设正包中正示例的比例在所有包中都是相同的，是一个定值。MILIS要对负示例做高斯核密度估计，当数据量较小时，估计是不准确的。

为解决上述问题，本文提出了基于模糊聚类的多示例集成算法ISFC（instance selection based on fuzzy clustering）。该算法对数据未做任何假设，是一个示例空间的方法，其将聚类和随机子空间的特性与多示例学习相结合，提出“正得分”的概念，降低了示例标签的歧义性，同时考虑到将负包中的负示例分类错误的代价更大，设计了一种改进的Bagging集成[17]策略，此外，该集成策略还解决了正包数量多、负包数量少情况下的类别不平衡问题。

1 相关知识

1.1 随机子空间法

子空间，又叫属性子集，是从初始的高维空间投影生成的低维属性空间。不同的子空间提供了观察数据的不同视角，显然，从不同的子空间训练出的个体学习器必然有所不同。随机子空间算法[18]依赖于输入属性的扰动，从初始属性集中提取出若干个属性子集，再用提取出的属性子集训练不同的基学习器。一方面，随机子空间法使得原始特征信息被充分利用，获得多样化的个体学习器；另一方面，由于属性数量的减少，节省了时间开销，避免了小样本问题，消除了无关和冗余属性对训练过程的干扰。

1.2 模糊C-均值聚类

模糊C-均值（FCM）聚类[19-20]是K-Means聚类的改进算法，它在K-Means的基础上引入了模糊理论，是一个软聚类算法。一般的聚类算法将数据硬划分，类别的划分界限是明确的，数据对象严格地归属于某个类，属于每个类的隶属度取值为0或1的离散值。但在现实世界中，数据对象具有多样性，在性态和类属方面存在着模糊性，通常不完全归属于某个类，而是同时归属于多个类，且属于每个类的程度是不同的。因此硬划分聚类不能很好地反映对象和类别间的实际关系。FCM建立了数据对象与类别归属的模糊不确定描述，对象同时归属于多个类，属于某个类的隶属度取值为[0，1]上的连续值，刻画了其属于每个类的程度，与硬聚类相比，更加客观地反映了数据对象与类别间的关系，提供了更加灵活的聚类结果，提高了聚类效果，与实际更为相符。

FCM是一个如式（1）的优化问题：

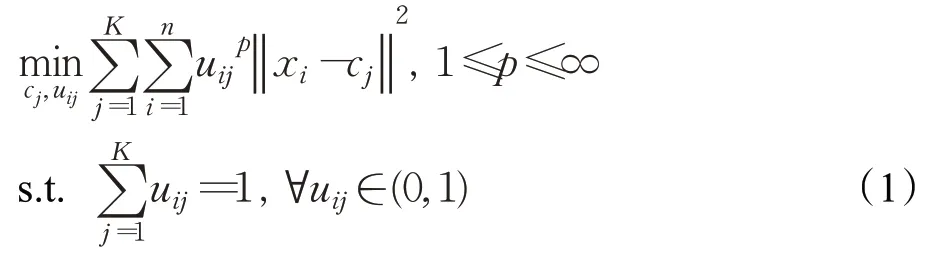
其中u ij表示样本x i属于簇j的隶属度，uij越接近1，则x i属于簇j的可能性越大。K是簇的数量，n是示例的数量，c j是簇j的中心，p是平滑系数，用于控制算法的灵活性。

FCM迭代地计算隶属度u ij和簇中心c j，以找到最佳隶属度划分，迭代的终止条件见式（2）：

其中s是当前的迭代次数，ε＞0是收敛阈值。

最终，可以得到一个隶属度矩阵U∈Rn×K。例如，示例x i的聚类结果对应于隶属度矩阵的第i行[0.2，0.5，0.15，0.15]，表明x i属于第二个簇的可能性最大。

2 结合模糊聚类的多示例集成

2.1 符号说明

D={(B1,L1),(B2,L2),…,(B m,L m)}是训练集，m是包的数量，B i={x i1,x i2,…,x ini}是第i个训练包，n i是第i个包的示例数量，x ij∈Rd是第i个包中的第j个示例，L i是第i个包的标签，Li∈{-1,1}。

2.2 基于方差贡献率的随机子空间

本文使用主成分分析（PCA）[21]对原始数据进行降维，PCA可以得到每个新特征的方差贡献率，方差贡献率表示一个特征包含的信息比例，能够度量一个特征的重要程度。因此，本文基于特征的方差贡献率构造随机子空间，方差贡献率越大的特征，被选为子空间特征的概率越大，方差贡献越小的特征，被选为子空间特征的概率越小。

子空间生成方法如下：

步骤1计算训练数据的协方差矩阵。

步骤2计算协方差矩阵的特征值λi以及对应的特征向量，一个特征向量对应一个新的特征方向，特征值用来描述对应特征方向包含的信息量。

步骤3计算第i个新特征的方差贡献率：

将其作为第i个新特征的权重，可以得到一个特征选择概率分布cr=(cr1,cr2,…,cr r)。

步骤4基于特征选择概率分布cr，选择特征子集。

一方面，该子空间的生成方法是高效的，因为特征重要性的评估，不需要花费额外的计算开销，而是重复利用了PCA时得到的方差贡献率；另一方面，生成的子空间是有效的，因为子空间是基于特征选择概率cr，而不是等概率生成的，包含信息越多的特征，越重要的特征，被选择的可能性越大。因此，与完全随机子空间相比，基于方差贡献率生成的子空间刻画数据的能力更强、更准确，各子空间之间也具有差异性，在其内训练学习器，效果可以得到保证。该子空间生成方法的伪代码见算法1。

算法1基于方差贡献率的随机子空间

输入：训练集D，保留的方差比例α，选择的特征比例β

输出：生成的随机子空间H

2.将数据居中Z=D-1·μT

4.计算特征值(λ1,λ2,…,λd)=特征值(Σ)

5.forr=1,2,…,ddo

7.end

8.降维，选择最小的r，使得f(r)≥α

9.用式（3）计算r个新特征的方差贡献cr=(cr1,cr2,…,cr r)

11.基于特征选择概率cr，从r个新特征中随机地选择h个特征，得到子空间H

2.3 示例的正得分

聚类是在对象无标记信息的情形下，基于对象之间的相似性，将对象分组的方法。多示例学习中，正包中示例标签是未知的，因此，可以通过聚类挖掘示例的信息。数据并不总是严格地属于某个分组，FCM聚类算法能够得到每个示例属于每个簇的概率，因此该算法中示例和簇的关系，与实际相符。但由于缺少数据的先验信息，如类别、形状、密度等，一次聚类的结果往往不佳，在不同的子空间对数据进行聚类，能够从不同的角度观察数据，得到更全面的信息。

正得分用于衡量示例标签为正的可能性，其借助了聚类和随机子空间法，并结合了负包中全部都是负示例这一基本多示例假设。正得分的基本思想如下：聚类后，对于正包中的一个示例，如果它所在的簇，大部分的示例来自负包，则表明它与负示例的相似度较高，那么其标签为负的可能性较大；反之，如果它所在的簇，只有很少的示例来自负包，则表明它与负示例的相似度较低，那么其标签为负的可能性较小。

正得分的计算方法如下：

步骤1用算法1生成R个随机子空间H1,H2,…,H R，H i⊆F，其中F是全空间。

步骤2将训练包中的所有示例在子空间H1,H2,…,H R上投影，然后在每个子空间中将示例用FCM聚类。在每个子空间中，示例都被划分为K个簇。

步骤3计算每个子空间的每个簇中，示例来自正包的比例。

对于子空间Ht中的第n个簇，示例来自正包的比例是：

其中：

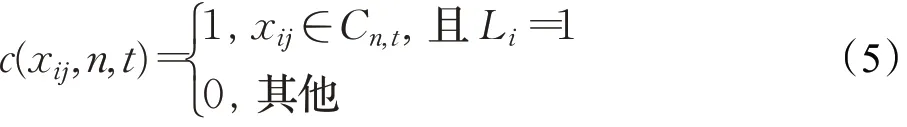
C n,t是在子空间Ht中聚类后，属于第n个簇的示例集合， |C n,t|是该集合的大小。

对于某一个子空间中的某一个簇，如果该簇中所有的示例都来自正包，那么P n(t)=1；如果该簇中所有的示例都来自负包，那么P n(t)=0。

步骤4计算示例x ij的正得分S ij：

其中：

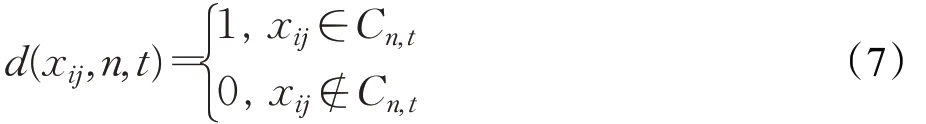
u(x ij,n,t)是在子空间H t中用FCM算法聚类后，示例x ij属于第n个簇的隶属度。

正得分用来评估示例标签为正的可能性，正得分越高，示例标签为正的可能性就越大，因此其降低了包中示例标签的歧义性。在目标识别和目标追踪等领域，只知道包的标签是不够的，还需要知道包中哪个示例最有可能是正例，此时，包中正得分最高的示例，就是寻找的目标。计算正得分的伪代码见算法2。

算法2正得分的计算

输入：训练集D，簇的数量K，子空间的数量R

输出：正得分S ij

1.fort=1,2,…,Rdo

2.用算法1生成子空间H t，然后将训练包中的示例在子空间Ht上投影，投影后，用FCM算法对示例进行聚类

3. forx ij∈Ddo

4.forn=1,2,…,Kdo

5.在子空间Ht聚类后，用式（4）计算第n个簇中，示例来自正包的比例Pn(t)，同时，得到示例xij属于第n个簇的隶属度u(x ij,n,t)

6.end

7.end

8.end

9.forxij∈Ddo

10.用式（6）计算x ij的正得分S ij

11.end

2.4 包代表示例的选择策略

从每个正包中选出一个示例，从每个负包中选出合适数量的示例，作为包的代表示例，然后将它们作为基分类器的训练子集，代表示例的标签是其所属包的标签。代表示例选择策略的基本思想如下：正包中至少包含一个正示例、一个假阳性和一个假阴性的示例都不一定导致错误的包标签；而负包中全部都是负示例，一个假阳性的示例一定导致错误的包标签[22-23]，所以，应尽可能地保证负包中的负示例被正确分类。

正包和负包中都是越“正”的示例，即正得分越高的示例，被选为代表示例的可能越大。对于正包来说，尽量避免了从中选出负示例；对于负包来说，其内全部都是负示例，理论上，负包中所有示例的正得分都很低，本文仍然给予与正类相关性更强的那些示例更大被选的可能性，这样能够迫使训练出的决策边界移向正类，尽量保证负示例被正确分类。

根据上述策略选择包的代表示例之前，需要借助一个soft-max函数，将示例的正得分S ij转化为一个[0，1]之间的概率值，该值表示示例被选为代表示例的概率，称为选择概率。选择概率与正得分是正相关的。对于任意一个包，其内包含的所有示例的选择概率的和为1，在包Bi中，示例x ij被选择的概率为P ij：

其中τ＞0是温度参数。当τ趋近于∞时，包中每个示例被选择的概率几乎相等；当τ趋近于0时，正得分最高的示例被选择的概率趋近于1，正得分最低的示例被选择的概率趋近于0。

2.5 集成设计

设计了一个Bagging集成的变体，由于支持向量机（SVM）的性能较好，所以将其作为基分类器。根据2.4节中的代表示例选择策略，为每个基分类器提供不同的训练子集。一般情况下，正包和负包中都选择一个示例；在正包数量多、负包数量少的情况下，灵活地从每个负包中选择合适数量的示例，从每个正包中仍然选择一个示例，这样在数据的层面上，解决了此种类别不平衡问题。因为负包中只包含负示例，所以无论从负包中选出多少示例，都不会导致错误的训练集，而严格地限制从每个正包中选择一个示例，是为了尽可能地避免从正包中选出负示例，从而防止训练出的分类器错误地标记负示例。

各基分类器的训练数据是基于示例选择概率被随机选择的，一方面，随机性保证了各基分器之间的差异性；另一方面，基于示例选择概率，而不是等概率，保证了各基分类器的质量。

2.6 包标签的预测

首先，每个基分类器为每个示例预测一个标签，第k个基分类器预测示例x ij的标签为yij,k，y ij,k∈{-1,1}；其次，采用简单平均法，结合各基分类器的预测结果，确定示例xij的最终决策值y ij，yij∈R。

其中M是集成规模；然后，根据标准多示例假设，确定包B i的最终决策值y i，y i∈R。

最后，将包Bi的决策值与0进行比较，确定包Bi的标签L i。

2.7 算法步骤

综上所述，本文提出的ISFC算法主要涉及5个步骤：

步骤1（生成子空间）基于特征的方差贡献率，生成多个随机子空间。

步骤2（计算示例的正得分）在生成的子空间，用模糊C-均值将训练示例聚类，再根据聚类结果，计算每个示例的正得分，评估示例标签为正的可能性。

步骤3（计算示例的选择概率）将示例的正得分转换为选择概率，为尽可能地避免从正包中选出负示例和将负包中的负示例分类正确，正包和负包中的示例，都是正得分越高，选择概率越大。

步骤4（抽取训练子集）基于示例选择概率，从每个包中随机选出代表示例，作为基分类器的训练子集，代表示例的标签是其所属包的标签。

步骤5（确定包最终的标签）采用简单平均法，结合各基分类器的结果。

ISFC算法的完整伪代码见算法3。

算法3结合模糊聚类的多示例集成算法

训练阶段

输入：有标记的训练包B l，集成规模M，子空间的数量R，子空间选取的特征比例β，簇的数量K，温度τ

输出：集成分类器C

1.用算法2计算每个示例xij的正得分Sij

2.用式（8）将正得分Sij转换为选择概率

3.C=Ø

4.fork=1,2,…,Mdo

5.基于示例选择概率Pij从每个正包中选择一个示例，从每个负包中选择合适数量的示例，构成训练子集S k，然后用S k训练基分类器C k

6.C=C⋃Ck

7.end

测试阶段

输入：未标记的测试包B u，集成分类器C

输出：预测的标记L u

1.fork=1,2,…,Mdo

2.forxij∈Budo

3.用基分类器Ck预测示例xij的标签y ij,k，然后用式（9）计算示例xij的决策值y ij

4.end

5.end

6.Lu=Ø

7.forB i∈Budo

8.用式（10）计算包B i的预测值yi，用式（11）确定包B i的标签L i

9.Lu=L u⋃L i

10.end

3 实验及分析

本文共进行了6组实验。实验一将ISFC与其他7个多示例算法进行了比较；实验二验证了正得分和代表示例选择策略的有效性；实验三验证了集成设计的有效性；实验四验证了方差贡献率度量的有效性；实验五分析了ISFC的参数敏感性；实验六分析了随机性对ISFC性能的影响。此外，还对ISFC算法进行了时间复杂度分析。

3.1 数据集

本文针对4个不同的任务：药物分析活性预测（Musk1、Musk2、Atom、Bonds、Chains），图像分类（Tiger、Elephant、Fox），文本分类（新闻组N.g.1、N.g.2、N.g.6、N.g.10、N.g.11、N.g.13、N.g.18）和火车挑战（EastWest），在16个多示例基准数据集上进行了实验，表1描述了它们的相关细节信息。特别地，Atoms、Bonds、Chains数据集中正包数量是负包数量的2倍，是类别不平衡问题。新闻组数据集（N.g.）中，正包中正示例的比列很低，约为3%左右[24]。

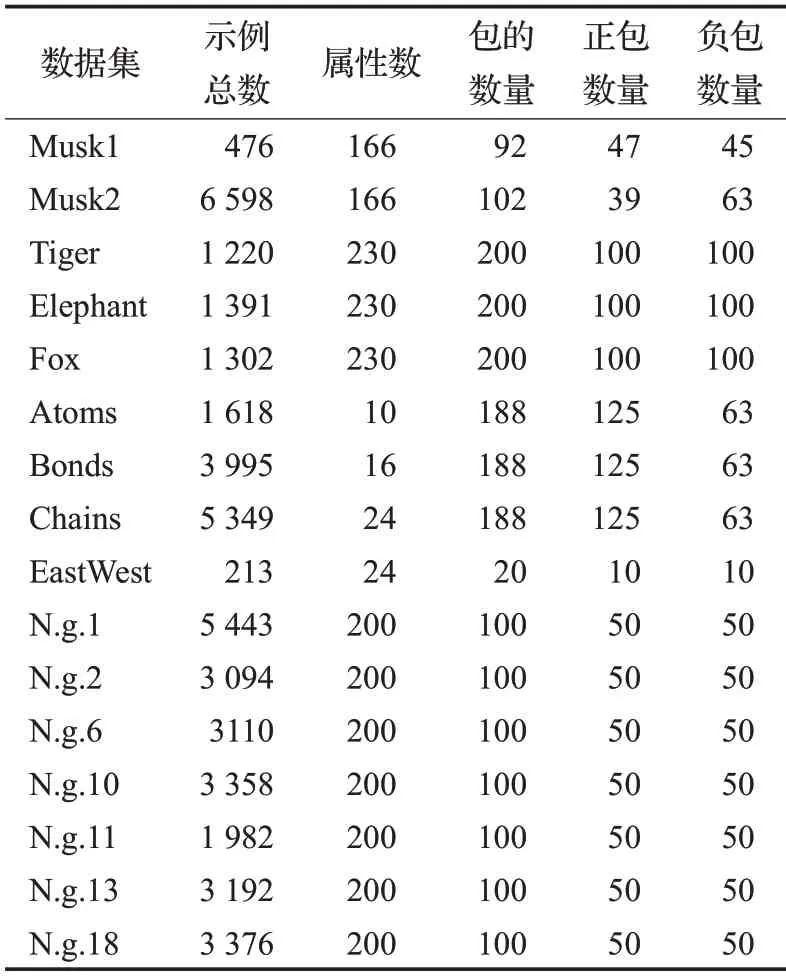
表1 实验数据集Table 1 Experimental datasets

3.2 实验设置

为避免所选数据的偏倚，在除EastWest的其他15个数据集上进行10次10折交叉验证，EastWest数据集包的数量较小，若同样采用10次10折交叉验证，会产生相同的训练和测试数据，所以EastWest数据集进行了9次5折交叉验证。本文报告了在所有测试数据上准确率和ROC曲线下的面积（AUC）的平均值，还报告了准确率95%的置信区间。

对比算法为Citation-KNN、MILBoost[25]、Simple-MI、CCE、K-means-encoding（BoW）、RSIS和MILDM。选择Citation-KNN，因为它是经典的包空间方法；选择Simple-MI，因为它假设正包中全部都是正示例；选择MILBoost，因为它是经典的多示例集成算法；选择CCE和BoW，因为它们都使用了聚类方法，此外，CCE也有SVM的集成过程；选择RSIS，因为它与ISFC也降低了示例标签的歧义性，ISFC是其改进算法；选择MILDM，因为它是性能很好的嵌入空间方法，优于当前大部分嵌入空间方法。

3.3 实验结果及分析

3.3.1 ISFC与其他多示例算法对比

表2和表3分别报告了算法的准确率和AUC，表2的最后一列是准确率的95%置信区间，两表的最后一行都是基于度量指标的算法平均排名。

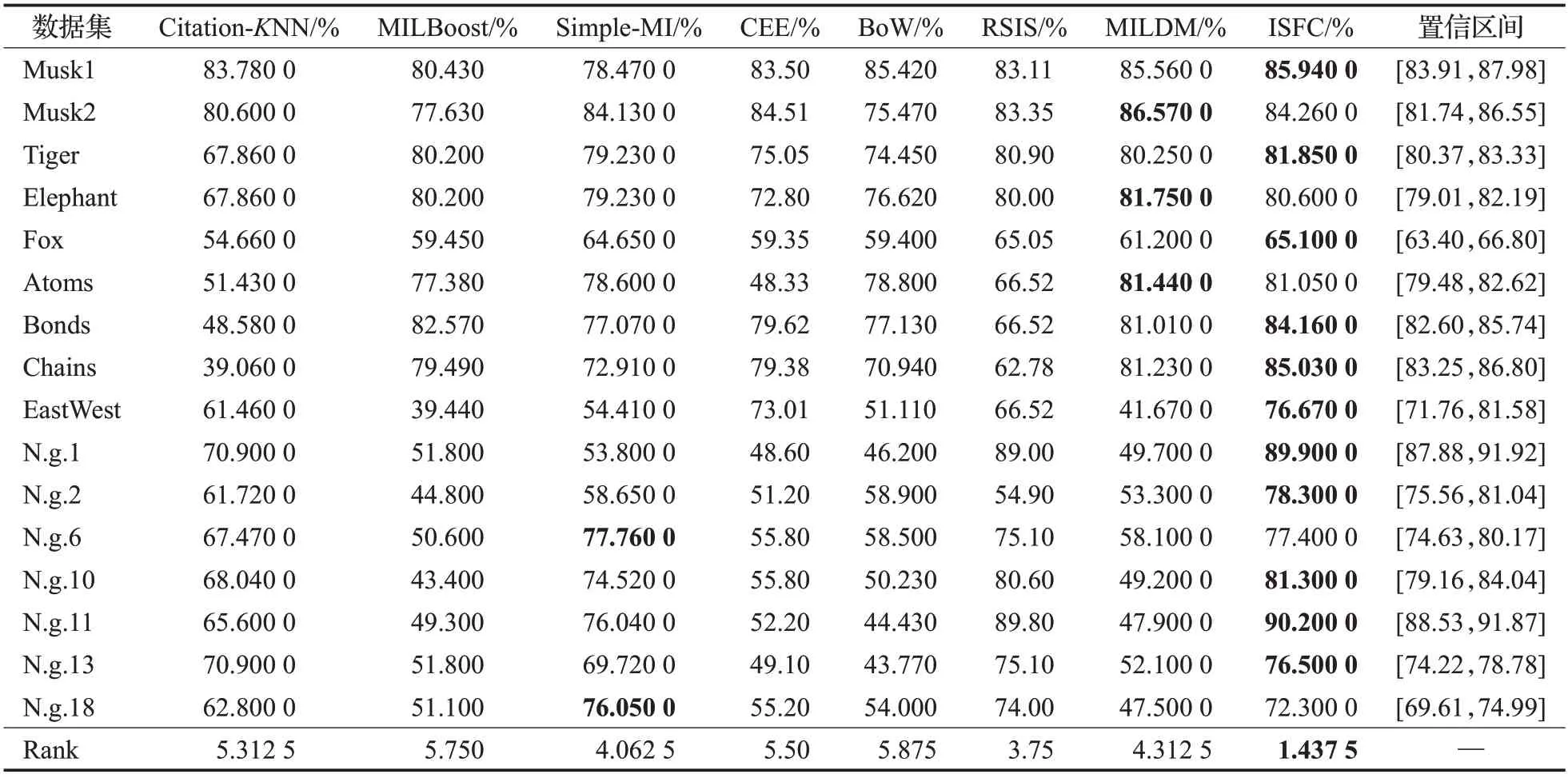
表2 准确率Table 2 Accuracy

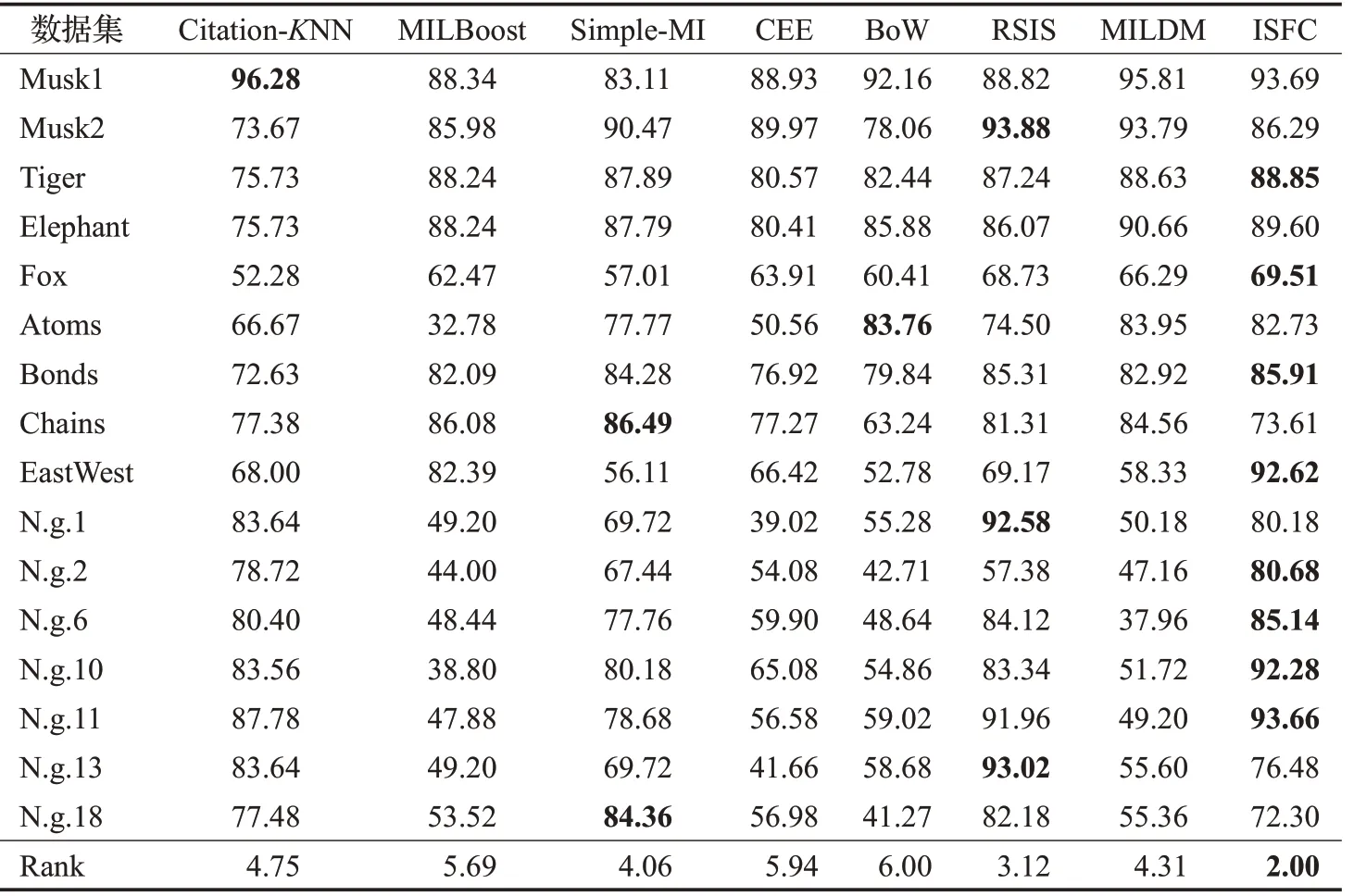
表3 ROC曲线下的面积Table 3 Area under ROC curve %

16个实验数据集中，示例的分布是不同的，每个正包中正示例的比例也是不同的，基于准确率和AUC，ISFC的平均排名都是最高的，这表明示例的分布和正包中正示例的比例对ISFC性能的影响不大。ISFC在9个数据集上取得了最高的准确率，在8个数据集上取得了最高的AUC。在Bonds、Chains、EastWest、N.g.2、N.g.13这5个数据集上，ISFC的准确率具有明显优势，分别比准确率第二高的算法高出3.15%、3.8%、3.66%、16.58%、1.4%；在EastWest、N.g.2、N.g.6、N.g.10、N.g.11这5个数据集上，ISFC的AUC具有明显优势，分别比AUC第二高的算法高出10.23%、1.96%、1.02%、8.72%、1.7%。特别地，Fox数据集很难分类，每个算法在该数据集上的分类效果都较差，相比之下，ISFC在该数据集上取得了最高的准确率和AUC。

表4～6分别报告了8个算法在3种不同学习任务上性能的平均排名，在文本和图像分类数据集上，基于准确率和AUC，ISFC的平均排名都是第一；在药物分子活性预测数据集上，基于准确率，ISFC平均排名第二；基于AUC度量，ISFC平均排名第三。ISFC在文本分类任务中非常成功，在5个新闻组数据集上，获得了最高的准确率和AUC。该类数据集中，正包中正示例的比例很低（3%左右），正包中的大部分示例对包的标签是无效的。包空间和嵌入空间的方法分别直接，间接地学习包的整体结构，如Citation-KNN、CCE、BoW、MILDM，当正包中有效示例非常少时，即正示例的比例较低时，正包的整体结构与负包的整体结构较为相似，此时正包和负包不容易区分，分类性能就会下降。

表4 图像分类任务上的平均排名Table 4 Average ranking on image classification tasks

表5 文本分类任务上的平均排名Table 5 Average ranking on text classification tasks

表6 分子活性预测任务上的平均排名Table 6 Average ranking on molecular activity prediction tasks

表7报告了类别不平衡问题（Atoms、Bonds和Chains数据集）中，8个算法性能的平均排名。基于准确率和AUC，ISFC均为第一，因为ISFC在代表示例选择过程中，从每个负包中选择了两个示例，在数据层面解决了类别不平衡问题，从而提高了分类性能。

表7 类别不平衡任务上的平均排名Table 7 Average ranking on imabalanced tasks

ISFC算法通过“正得分”衡量了示例为正例的可能性，降低了正包中示例标签的歧义性。RSIS算法[4]是降低示例标签歧义性的典型方法，也衡量了示例为正例的可能性。理论上，一方面，ISFC的子空间是基于特征的方差贡献率生成的，包含信息量越多的特征被选为子空间特征的概率越大，而RSIS算法中，各特征被选为子空间特征的概率是相等的，相比之下，ISFC生成的子空间对数据的刻画更加有效，在其内训练的学习器性能更好；另一方面，ISFC在子空间中用FCM算法将示例聚类，得到了每个示例属于每个簇的隶属度，并将其引入到正得分的计算，而RSIS用K-Means算法将示例聚类。现实情况下，示例通常同时属于多个簇，与K-Means相比，FCM这种软聚类与实际更为相符，因此，与RSIS相比，ISFC通过方差贡献率和模糊隶属度，衡量示例为正例可能性的方法更加准确可靠。从实验结果来看，ISFC性能的平均排名优于RSIS，其在15个数据集上的准确率高于RSIS，在11个数据集上的AUC高于RSIS，同时在表4～7表明其在各类多示例任务上的表现也都优于RSIS。因此，ISFC算法降低示例标签歧义性的能力更强。

3.3.2 ISFC与完全随机地选择代表示例对比

选出的代表示例作为基分类器的训练子集。对比实验完全随机地选择代表示例（简称随机方法），它与ISFC的唯一区别在于代表示例的选择方法，其他过程和参数完全相同。随机方法包中每个示例被选择的概率是相等的，ISFC是基于计算得到的示例选择概率Pij选择示例。

如图1展示了ISFC与随机方法的成对性能比较，图（a）是准确率，图（b）是AUC，红线表示函数y=x，横轴表示随机方法，纵轴表示ISFC。如果一颗绿星位于红线的左上方，则表明ISFC在相应的数据集上表现更好。图（a）上，绿星均位于红线的左上方，表明在所有实验数据集上，ISFC的准确率均高于随机方法。大部分绿星与红线的距离较远，表明在大多数实验数据集上，ISFC具有明显优势，如在Musk1、Elephant、Chains、East-West和N.g.11上，分别高出随机方法2.25%、5.05%、18.57%、12.23%、28.6%；图（b）上，大部分的绿星位于红线上方，表明在大部分数据集上，ISFC的AUC高于随机方法，如在Musk1、Elephant、EastWest、N.g.2、N.g.11和N.g.18上，分别高出随机方法4.1%、5.57%、5%、13.16%、16.24%、4.84%，优势也较为明显。因此，本文提出的代表示例选择策略是有效的。

图1 ISFC与随机方法的成对性能比较Fig.1 Pairwise performance comparison between ISFC and random methods

与随机方法相比，ISFC的优势源于两方面：首先，ISFC通过正得分评估了包中每个示例为正例的可能性，认为每个示例为正类的可能性是不同的；而随机方法认为包中每个示例为正类的可能性是相同的，ISFC是更合理的，正得分尽可能地保证选出有用的示例，降低从正包中选出负示例的概率。其次，ISFC的代表示例选择策略考虑到将负包中负示例分类错误的代价更大，而随机方法没有考虑到该问题，ISFC规定：正包和负包中，都是正得分越高的示例，被选择的概率越大，这样迫使分类器的决策边界偏向正类，尽可能地避免将负示例预测错误，从而提升包标签预测的准确率。

3.3.3 ISFC与单分类器对比

对比实验单分类器与ISFC的唯一区别在于集成规模M的不同，单分类器中设置M=1，其他过程和实验设置与ISFC完全相同。

如图2展示了ISFC与单分类器的成对性能比较，所有的绿星都位于红线的左上方，这表明在所有的实验数据集上，ISFC的准确率和AUC都高于单分类器。在不同的数据集上，ISFC中的集成规模M是不同的，但都不同程度地提高了分类器的性能，如在Musk2、Fox、Chains、N.g.1、N.g.13数据集上的准确率分别高出单分类器6.34%、7.6%、4.42%、14.3%、19.6%；在Elephant、Fox、N.g.1、N.g.10、N.g.13数据集上的AUC分别高出单分类器10.35%、12.01%、17.02%、14.04%、36.76%。这表明各个基分类器是有效的，且它们之间具有差异性，集成设计是成功的。

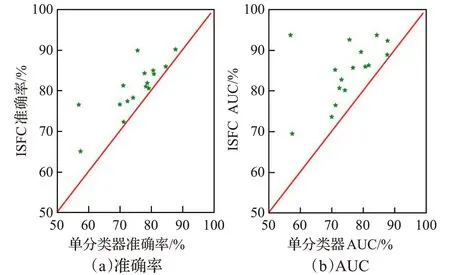
图2 ISFC与单分类器的成对性能比较Fig.2 Pairwise performance comparison between ISFC and single classifiers

3.3.4 方差贡献率的有效性验证

为验证ISFC算法中特征方差贡献率度量的有效性，本文在14个数据集上进行了一组ISFC与子空间是完全随机生成的对比实验（简称随机方法2），即每个特征被选为子空间特征的概率是相等的。实验结果见表8，ISFC在所有数据集上的准确率和F分数都高于随机方法2，在除Musk2、Tiger和Atoms外的其他11个数据集上，ISFC的AUC均高于随机方法2，特别地，在Musk1、EastWest、N.g.2、N.g.6、N.g.11、N.g.18数据集上，ISFC的优势较为明显，准确率分别高出2.23%、7.78%、27.90%、10.20%、10.00%、22.30%，AUC分别高出3.55%、9.72%、21.54%、8.62%、4.98%、28.04%，F分数分别高出2.11%、3.70%、14.09%、5.94%、7.37%、4.35%，因此方差贡献率度量是有效的。

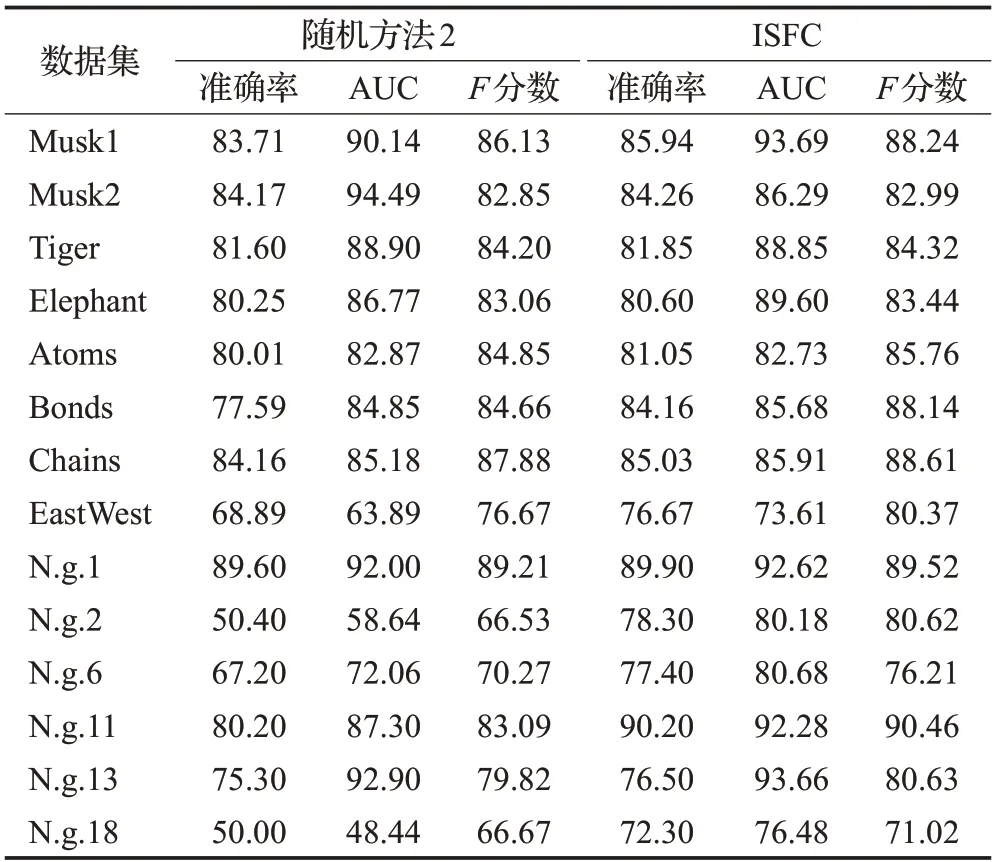
表8 ISFC与随机方法2的实验结果Table 8 Experimental results of ISFC and random method2%

3.3.5 参数敏感性分析

本文在5个数据集上研究了参数变化对分类性能的影响，ISFC算法共涉及5个参数，生成子空间的数量R、子空间选取的特征比例β、聚类时簇的数量K、正分数转换为示例选择概率时的温度τ、集成规模M。

从图3（a）可以看出，在所研究的数据集上，当集成规模M＞10时，准确率的波动范围是0.45%到1.8%，标准差在0.17%到0.5%之间，因此它对ISFC算法的性能没有显著影响，可以粗略调节。集成规模不敏感的原因是随着集成规模的增加，训练程度逐渐加深，分类器需要学习的模式已经基本学到，此时再继续增加集成规模，模型的表达能力不会大幅提升了。本文的集成设计是Bagging的一种变体，是并行式集成，该表现与Bagging和随机森林类似，起始性能通常不佳，特别是集成中只包含一个基分类器时，但随着基分类器数目的增加，它们的泛化误差会收敛到一个更低的值，性能趋于稳定。

从图3（b）可以看出，子空间的数量R＞100时，准确率的波动范围是0.6%到1.33%，标准差在0.17%到0.43%之间，因此该参数对ISFC算法的性能影响不大，可以粗略调节，其不敏感的原因与集成规模相同，当学习达到一定程度，性能趋于稳定，继续增加规模，性能不会显著提升。

从图3（c）可以看出，FCM聚类中簇的数量K是一个比较敏感的参数，在不同的数据集上，性能的变化没有一致的趋势，这是因为最佳簇的数量K与数据集本身有关，数据实际的分组情况是未知的，因此，该参数需要仔细调节。

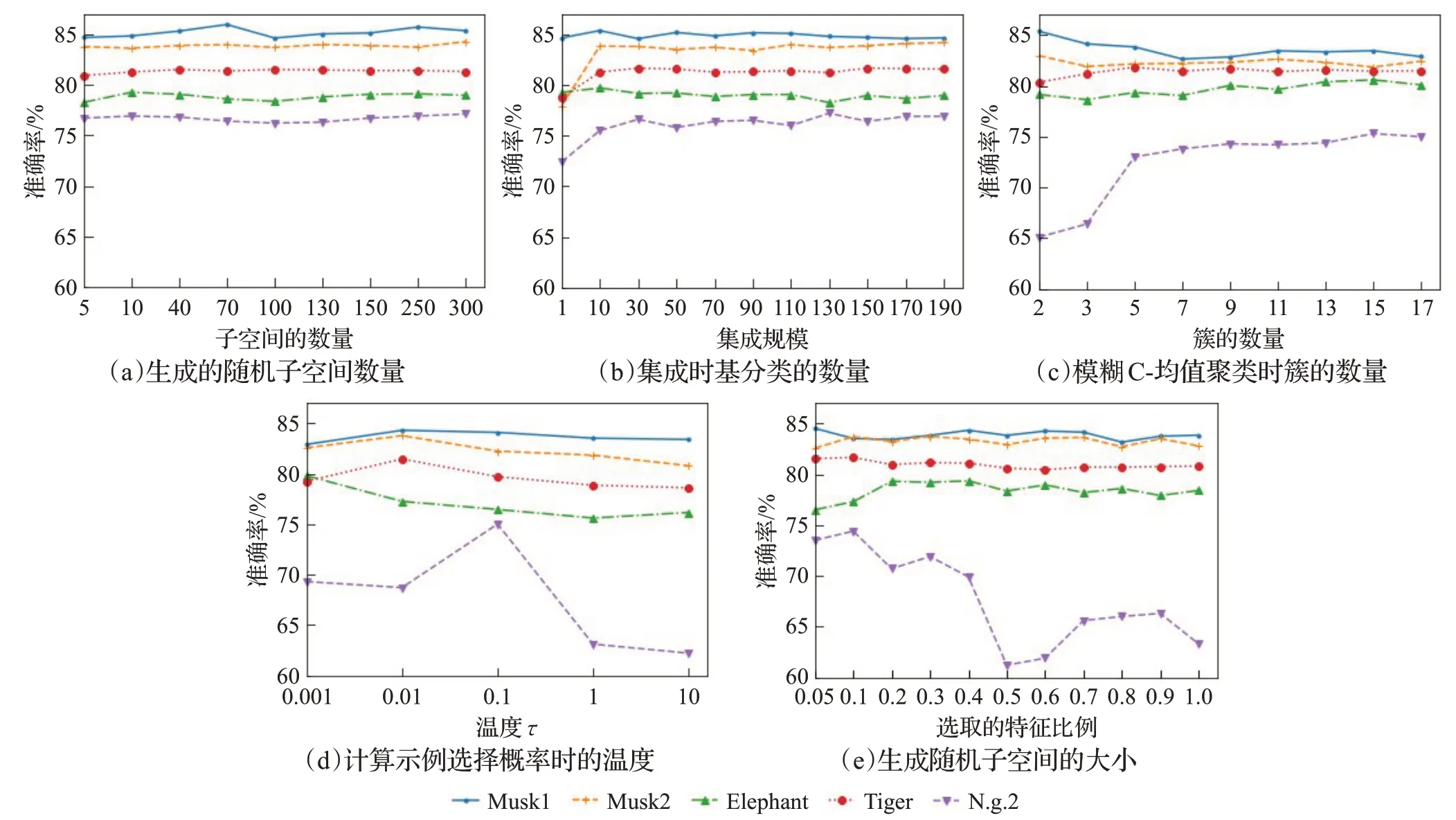
图3 ISFC在5个数据集上不同参数的准确性Fig.3 ISFC’s accuracy of different parameters on 5 datasets

从图3（d）可以看出，温度τ是一个非常敏感的参数，当它在{0.001，0.01，0.1，1，10}范围内变化时，准确率的波动范围是1.4%到12.8%，标准差在0.5%到4.5%之间。如2.4节所述，如果温度τ较低，则每次从包中选出的代表示例都是相同的，各基分类器的训练子集非常相似，降低了基分类器之间的多样性；如果温度τ较高，那么每个示例被选择的概率几乎是相同的，与3.3.2小节中的对比实验随机方法非常接近，增加了从正包中选出负示例的风险，削弱了正得分的作用。该参数与正包中正示例的比例有关，而正包中正示例的比例是未知的，所以需要仔细调节。

从图3（e）可以看出，生成子空间时所选特征的比例β在Tiger数据集上，对性能几乎没有影响；在N.g.2数据集上，有显著影响；在其他3个实验数据集上，有轻微影响。总体来看，随着所选特征比例β的增加，准确率逐渐降低，原因是当所选特征比例过高时，会降低随机子空间之间的多样性，进而影响聚类的结果和正得分。实验结果表明，β不宜过大，通常小于0.4时，效果较好。

3.3.6 随机性分析

ISFC算法中有两个随机过程：随机子空间的特征是基于特征的方差贡献率随机生成的，各基分类器的训练数据是基于示例选择概率随机选择的，因此本小节研究随机性对ISFC算法性能的影响。

从理论上分析，一方面，子空间是基于特征的方差贡献率生成的，包含信息量越多的特征，被选择的概率越大，包含信息量越小的特征，被选择的概率越小，这保证了各个子空间的有效性；另一方面，各基分类器的训练数据是基于示例选择概率随机选择的，示例选择概率是由正得分转换而来的，代表示例选择策略规定：在正包和负包中，都是正得分越高的示例，被选择的概率越大，包中每个示例被选择的概率是不同的。一方面，从正包的角度来看，该选择策略尽量避免了从正包中选出负示例，进而避免训练出的示例级分类器预测出假正例；另一方面，从负包的角度来看，使得示例级分类器的决策边界移向正类，增加了真负例的数量。因此，包的分类效果得到了保证，随机性对分类器性能的影响不会很大。

从实验上，本文在Musk1、Elephant、EastWest、Bonds、N.g.10和N.g.11数据集上进行实验。在一个数据集上，用相同的实验设置（交叉验证的划分和参数）重复实验100次，然后计算100次实验结果的标准差，实验结果见表9，在Musk1、Elepahnt、Bonds、N.g.10、N.g.11数据集上，准确率的标准差分别为0.42%、0.32%、0.17%、0.79%、0.38%，AUC的标准差分别为0.43%、0.32%、0.19%、0.86%、0.38%，均较小，因此，随机性对分类器性能的影响不大。

表9 100次重复实验性能的标准差Table 9 Standard deviation of performance for 100 repetitions %

3.3.7 时间复杂度分析

ISFC的训练阶段包括两个部分：计算正得分和训练集成分类器。在正得分的计算阶段，对所有训练示例进行FCM聚类，需要计算训练示例和簇中心的距离，FCM聚类的时间复杂度是O(nr KlR)，其中n为示例的数量，r为数据的维数，K为簇的个数，l为迭代次数，R为子空间的数量。在训练集成分类器时，从每个包中选出的代表示例作为SVM的训练数据，时间复杂度为O(m2rM)，这表明包的数量m对训练时间的影响，比示例的数量n影响更大。

4 结束语

本文提出了一个新的多示例学习集成算法ISFC，该算法对示例的分布和正包中的正示例比例不做任何假设，同时解决了正包数量多，负包数量少的类别不平衡问题。ISFC算法利用随机子空间法和模糊聚类算法，定义了示例的正得分，消除了正包中示例标签的歧义性；然后考虑到多示例学习中，将负示例分类错误的代价更大，基于正得分设计了包代表示例的选择策略；最后，选出的代表示例作为基分类器的训练子集，训练集成分类器。

在今后的工作中，可以对包进一步研究，使得从包中选出示例的数量更加灵活。这样做有两点好处：第一，类别不平衡问题可以在数据层面上进一步解决；第二，随着样本量的增加，可以学习到更好的分类器。此外，正得分可以应用于一些多示例学习的迭代方法，如MILES、MILIS和MIRSVM，将每个包中正得分最高的示例作为初始代表示例，以减少迭代次数。