ACPR50S试验堆压力容器椭圆封头数控加工工艺研究

徐晨洲 袁宗焕

(二重(德阳)重型装备有限公司，四川618000)

收稿日期：2021-07-12

ACPR50S试验堆压力容器是ACPR50S反应堆的核心设备，主要包括整体顶盖、下封头、法兰接管段筒体、堆芯段筒体等零部件。其中，椭圆下封头是压力容器制造中的难点之一，其内曲面为椭球面，外曲面为近似椭球面，控制工件法线方向壁厚的均匀性是其加工制造的难点。本文主要研究椭圆封头内、外曲面的数控加工工艺方法。

1 零件结构及精度要求

1.1 几何特征

该零件为椭球体类结构，由上部圆柱面，下部椭球体类曲面组合而成，如图1所示。椭球体内曲面轮廓线为长轴与短轴比为2∶1的椭圆，在椭圆长轴端点上与上部内圆柱面相接，并形成一个20 mm的内台阶面。椭球体外部曲面是与内曲面保持120 mm等壁厚的曲面，且上部圆柱曲面在51 mm处相切。

图1 椭圆封头Figure 1 Elliptical head

1.2 精度要求

该零件内椭圆长轴尺寸直径公差为0.5 mm，半径公差为0.25 mm，精度等级达到IT9级，精度要求较高；壁厚公差为0.5 mm，对于线性尺寸来说，其精度等级为IT13，属于普通精度等级，但要满足内、外曲面任意一点的法线壁厚均一致，且公差为0.5 mm，其加工难度就增大了很多。工件各表面的粗糙度为Ra6.3，一般数控机床均能满足要求。

2 数控加工工艺分析

从该零件的几何特征及精度要求分析，可得出其制造加工的难点在于控制内、外曲面等壁厚达到要求，以及控制厚度公差及精度。

2.1 工艺系统误差分析

零件加工过程中影响零件壁厚公差尺寸的因素较多，对于本椭球体类工件主要包括工艺系统误差、工艺性误差、数控加工数学模型及编程方法的误差。

(1)工艺系统误差主要来源于数控机床，具有不可压缩性，在工艺过程中必须考虑。本零件为回转类零件，需用4 m左右的数控立车加工。因此，工艺系统误差主要包含工作台几何精度、刀架(横梁)垂直运动与工作台回转精度、定位与重复定位的精度、刀具系统刚性、夹具系统的刚性、工件切削热变形等，这些因素均会影响零件的内、外轮廓精度，占用壁厚公差，使壁厚公差实际可调整范围变窄。

(2)工艺性误差与加工工艺方法、工艺手段有着直接的因果关系，属于非原理性误差。在制定工艺过程中要充分考虑加工流程、工艺基准、装夹方式、切削参数等因素，制定合理可操作的工艺方案，尽量减少工艺性误差。

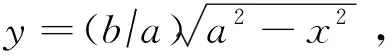
图2 等距m外曲线与外椭圆曲线示意图Figure 2 Schematical diagram of outer curve with equidistant m and outer elliptic curve

2.2 主要工艺措施

针对本零件特点及精度要求，可以采取以下工艺措施，提高零件加工精度。

(1)合理选用数控加工设备，调整数控设备的精度指标，包括工作台回转精度、刀架垂直度、重复定位精度等，使其设备精度累计误差控制在0.2T(图纸公差)范围内；

(2)工艺基准与设计基准统一，且工序前后基准重合，均按零件内曲面为基准，可以有效地降低不同加工工位的误差；

(3)加工过程中，采取粗精分开，分多刀次加工的原则，有效减少工件内应力与切削热变形引起的误差；

(4)增加内、外曲面、端面装夹、定位工装，控制工件找正精度(水平、垂直，圆度)，使累计误差控制在0.2T(图纸公差)范围内；适当加大刀具截面尺寸，提高工艺系统的刚性；

(5)合理选择数控程序的切入、切出角度，减少零件加工残留，提高工件表面加工质量；

3 数控加工

零件数控加工过程，实际就是将零件的几何特征转换成能被数控机床识别的空间坐标点，以该坐标点来驱动数控机床，以达到数控机床的运动轨迹符合零件几何特征的一个过程。

现有数控设备均只有线性插补和圆弧插补，即对线性几何特征只需得到线性特征的起、终点坐标，对圆弧几何特征只需得到圆弧特征的起、终点坐标和半径值就可控制机床加工出线性和圆弧几何特征。对于其他曲线几何特征，将其几何特征信息转化为机床能识别信息，是数控加工中研究的重点和难点。利用有效几何特征信息，建立零件轮廓的数学模型，求解出相应数学模型的参数方程，是准确转化零件几何特征的有效手段，也是数控加工常用方法。求解出零件轮廓参数方程后，只需按参数方程进行编程得出NC代码，以NC代码控制数控机床运动轨迹便可加工出相应的几何特征。

3.1 参数方程

根据本零件的几何特征，内轮廓线为标准椭圆曲线，外轮廓线为与内椭圆曲线上各点法线方向距离相等的曲线。

椭圆标准参数方程：

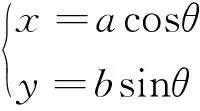
(1)

椭圆外等距曲线方程：

如图3(a)所示，设平面椭圆曲线f(x)上任意一点P沿着该点法线方向向外移动一段距离m，所得到的轨迹为F(X)，即F(X)为f(x)的外等距曲线。

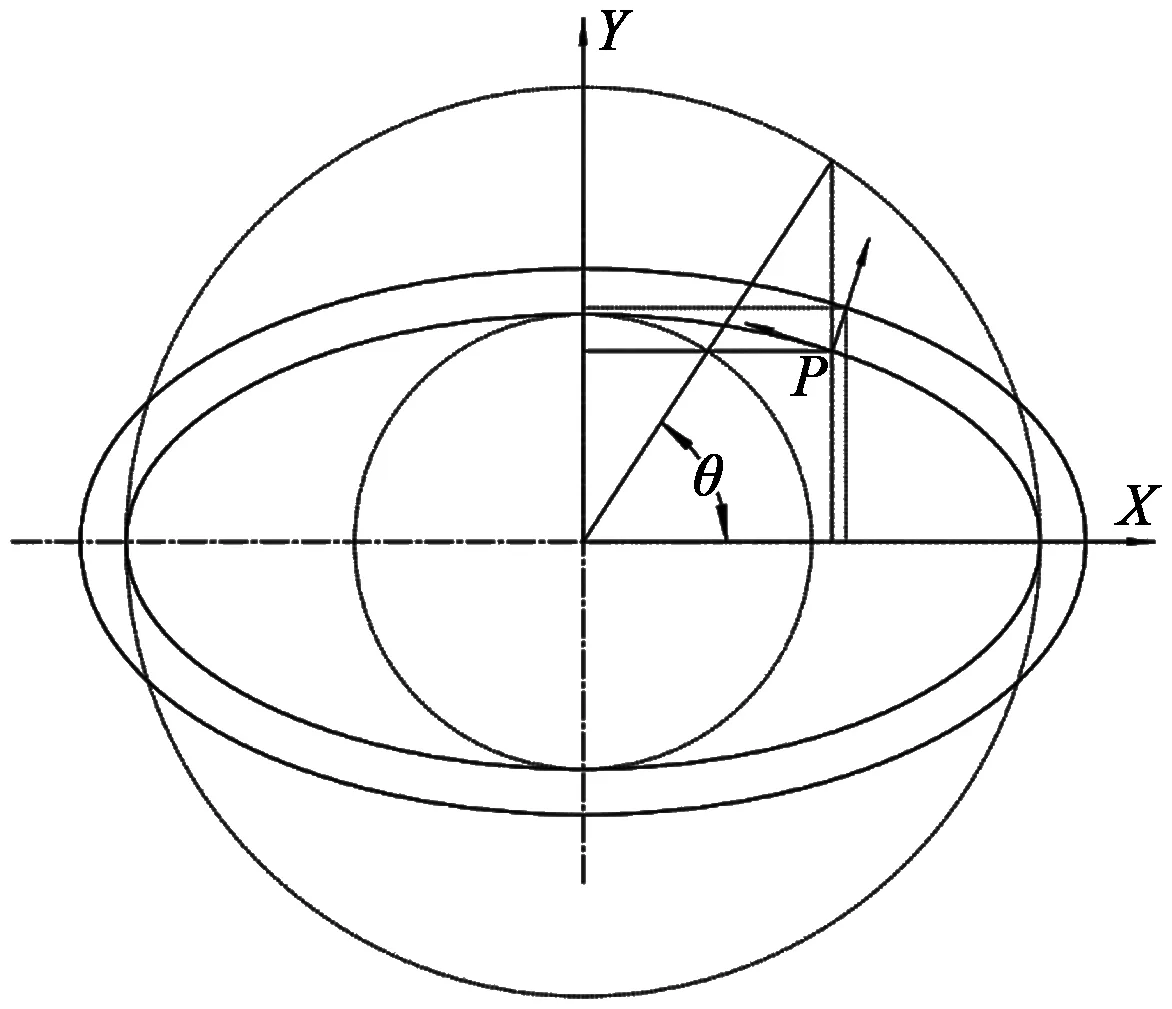
图3 椭圆外等距曲线Figure 3 Outer equidistant curve of elliptic curve

式中，i、j表示在坐标轴X、Y上的单位向量，法向量指向等径曲线为正。

根据外等距曲线法向距离相等，F(X)=f(x)+m·n，则有：

可得出椭圆外等距曲线的参数方程：

(2)

将(2)式整理后得：

(X-acosθ)2+(Y-bsinθ)2=m2

(3)

由式(2)与式(3)可以得出，椭圆的等距曲线为圆心在已知椭圆上且半径为m的圆族包络线，不是椭圆曲线。利用切向量与法向量之间的关系，还可以求出其他任意曲线f(x)的等距曲线。

3.2 数控编程

3.2.1 圆弧逼近法

在椭圆曲线的加工过程中常会用到圆弧逼近法完成椭圆曲线的近似加工，即将椭圆曲线分为若干(有限)弧段，每个弧段上选取3个点(含起、终点)确定一段圆弧，就可以用若干首尾相连的圆弧段逼近椭圆曲线。

如图4所示，在椭圆曲线上任取3点A、P、B，形成弧段AB，δ为拟合圆弧与椭圆曲线的最大误差，只要δ≤T(图纸公差)，则拟合圆弧满足要求。根据曲线曲率半径公式、弦长公式以及公差T，计算出最大L，然后使LAP≤L，计算P点坐标(已知起始点A坐标)，依次类推计算B点坐标，通过A、P、B计算出拟合圆弧半径R，则该弧段拟合计算完成。然后利用相邻拟合圆弧端首尾相接(共点)性质，同理计算剩余各段圆弧的参数。

图4 圆弧逼近法拟合计算Figure 4 Fitting calculation by arc approximation method

对于椭圆外等径曲线，可以将椭圆拟合圆弧偏置一个m，然后利用R/(R+m)的比例关系计算得到外等径曲线的拟合圆弧参数。

如果椭圆曲线轮廓精度要求较高，则拟合圆弧的计算量很大，计算错误概率较高，不适合用圆弧逼近法。通常圆弧逼近法适用于零部件轮廓精度不高的曲线数控加工。

本零件内椭圆曲线长半径为1156 mm，短半径为578 mm，其长半轴的尺寸公差为0.25 mm。按0.2 mm公差计算，需要9个模拟圆弧段才能得到符合要求的近似椭圆曲线，然后以G02圆弧编程即可。例如第一个拟合圆弧的起点为(1156，0)，终点为(1145.082，79.251)，半径为293.094，则该拟合圆弧的程序段为：

G01 X1156 Z0

G02 X1145.082 Z79.251 R293.094

3.2.2 参数编程法

参数编程不仅可以实现特定数值下的一次加工，也可以实现同类型不同数值下的其他加工，只需改变参数赋值即可，操作灵活简便。通过改变增量参数的大小，调整切削步长，改变密化点数量，以匹配不同零件的精度要求。事实上，增量参数固定时，编程轨迹与曲线本身存在一个δ的误差，只是增量很小时，误差δ可忽略不计，不影响加工精度。

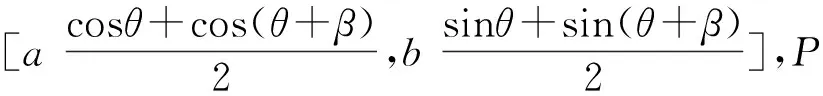
经计算简化后得：

当β=0.1°，0°≤θ≤90°时，δmax=4.4×10-4mm，基本可以忽略不计。

图5 参数编程示意图Figure 5 Schematical diagram of parametric programming

设定变量参数与增量参数后，可按内、外轮廓线的参数方程式(1)和式(2)进行编程，以SIEMENS系统R参数编程为例，外轮廓线部分程序段如下：

(1)设定参数及赋值

R11=578.313；Z轴方向椭圆半径

R12=1156.625；X轴方向椭圆半径

R13=121.75；壁厚

R21=0；起始角度

R22=0.1；角度增量

R23=R21；循环角度

R24=90；终止角度

(2)循环及切削

MARK1：

IF R23>R24 GOTOF MARK2

R31=R11*sin(R23)+R13*R12*sin(R23)/SQRT(R12*R12*sin(R23)*sin(R23)+R11*R11*cos(R23)*cos(R23))

R32=R12*cos(R23)+R13*R11*cos(R23)/SQRT(R12*R12*sin(R23)*sin(R23)+R11*R11*cos(R23)*cos(R23))

G01 X=2*R32 Z=R31

R23=R23+R22

GOTOB MARK1

3.2.3 CAM辅助编程法

对于几何特征十分复杂的零件，各轮廓线的参数方程很难计算出来，通常会借助CAM编程软件辅助编程。CAM辅助编程的NC代码几乎是以点到点的方式呈现，因此，CAM辅助编程具有唯一性。即同一程序只能在相同零件、相同状态、相同工序、相同工位的情况下相互使用，否则不能使用。CAM辅助编程的零件轮廓精度主要取决于三维模型的精度和切削参数的匹配性。图6为CAM辅助编程示意图。

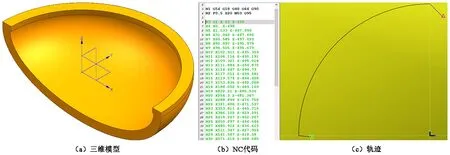
图6 CAM辅助编程示意图Figure 6 Schematical diagram of CAM auxiliary programming

4 结论

(1)椭圆的等距m线不是椭圆，而是圆心在已知椭圆上且半径为m的圆簇包络线，是样条曲线。

(2)对于该椭圆封头的内、外曲面轮廓线均可用圆弧逼近法、参数编程法、CAM辅助编程法进行数控编程，达到其图纸精度要求。一般而言，圆弧逼近法多用于轮廓精度要求不高的零部件加工；参数编程法多用于零件轮廓为标准曲线或能求解出参数方程的零部件加工，同类型曲线只需更改参数赋值即可，灵活方便；CAM辅助编程法具有唯一性，多用于形状复杂的零部件加工。

(3)影响椭圆封头加工精度的主要因素是工艺系统误差、加工工艺性误差、数控加工数学模型误差。合理地对这三项因素进行分析与控制，制定合理的工艺方案，能有效地降低加工误差，提高加工精度。

(4)文中所述的工艺方法均成功应用于ACPR50S试验堆压力容器椭圆下封头或其他项目椭圆封头制造，所加工零件符合技术参数要求，质量良好。