带有启动时间和两类故障的M/M/1系统均衡策略分析

汪文杰， 刘力维， 叶晴晴

(1. 南京理工大学 理学院， 南京 210094；2. 南京信息工程大学 数学与统计学院， 南京 200044)

0 引 言

生活中处处存在排队现象，看得见的有火车站排队检票、物流中心货物的调配等；看不见的有信号的接收与传输等。在排队时经常出现这样一种现象：在某些时段服务台前排队的顾客较多，在某些时段服务台前又没有顾客。这是因为顾客会根据自身需求选择进入队列时间，这就要求顾客和服务台从经济学角度去衡量自身的预期收益。排队论与经济学的结合，考虑了人的主观能动性，重点放在顾客接受完服务后获得的利益。同时，服务提供商也会让服务台进行不定时的休息，从而降低成本获得更高的利润。Naor[1]率先使用博弈论研究排队系统，得出了顾客在知晓系统顾客数时的均衡进队策略，同时提出了通过收取过路费的方式使顾客改变其进队策略，让社会平均收益达到最高；Edelson与Hildebrand[2]针对文献[1]的模型，讨论了在系统信息完全不可见条件下顾客的进队策略以及社会最优策略；Kerner[3]分析了可见情形下的M/G/1排队系统，由于服务时间分布丧失了无记忆性特征，整个过程变得复杂，不同的服务时间概率分布会让顾客的聚集偏好(FTC)和聚集厌恶(ATC)都可能发生。

由于系统的不可靠性，故障随时都可能发生。Economou等[4]首先考虑了系统中的故障问题，他们给出了在完全可见信息水平下，带有完全故障特性和立刻维修特性队列中顾客的止步门限值；Li等[5]分析了不同信息水平下带有不完全故障队列中的顾客策略选择问题；Xu等[6]在文献[5]的基础上建立了带有部分故障特性和推迟修理的排队情景，分析了顾客在完全可见以及完全不可见时的止步策略以及相应的社会预期收益；张淞钛和徐秀丽[7]讨论了信息几乎不可见和完全可见条件下带有两种故障类型的社会平均收益和顾客进队问题；对于需要延迟启动的排队系统，Burnetas与Ecomomou[8]率先从经济学角度进行探讨，给出了信息完全可见、部分可见、不完全可见和完全不可见情形下的顾客进队门限以及社会预期收益；Sun等[9-10]又在Burnetas模型基础上加入了关闭时间，研究了系统信息可见和不可见时排队系统中顾客进队策略；Chen等[11]将N策略和启动时间两种休假方式同时引入排队系统，给出了在完全可见和完全不可见时的单位时间费用函数、社会收益等系统性能指标；Chen等[12]推导了在完全可见、部分可见以及完全不可见情形下，带有启动时间和完全故障的排队系统顾客均衡策略和优化策略，并分析了不同参数以及信息水平的影响。

随着现实需求逐渐细致，需要从更多的角度提高经济效益，抽象出的排队模型也变得复杂起来。如在使用大型计算机处理不同任务时，设备需要先开机，由于性能的差异和任务种类的不同，设备可能会出现处理速度变慢或者死机的情况；冬天汽车发动机的启动需要一段预热时间，恶劣天气会给汽车动力系统带来很多不安全因素，造成汽车的抛锚，这要求建立一个新的模型对此类工作系统进行指导，因此考虑带有两类故障和启动时间的服务系统具有很强的现实意义和应用价值。

1 模型描述

考虑一个有两类不完全可靠特性和延迟启动的M/M/1排队系统，顾客按照进入顺序等待服务，服务台总是先服务先进入系统的顾客。当服务台处于休假状态时，此时抵达系统的顾客不会立刻被服务，服务台需要经过一段启动时间才会进入正常工作状态，但启动时间长度是不确定的。系统的服务柜台具有不可靠性，即服务台有使用寿命，在服务的过程中随时可能因为“寿命终了”而发生不同程度的损坏，且顾客具有“故障厌恶性”，即当顾客发现服务台处于任意一类故障状态时，就不会选择进入队列。服务台有两种故障类型：完全故障，即系统丧失全部服务能力，立刻进行维修，修好后接着为顾客服务；不完全故障，即系统仍然保有部分服务能力，但服务速率降低，直至服务完系统中所有剩余顾客后进行维修。设系统提供的服务速率在正常工作时是μ，在不完全故障时是μ0，两类服务时间都呈指数分布而且有μ0<μ。对于服务台，不完全故障发生的过程和完全故障发生的过程都是泊松过程，参数分别为ε1和ε2。对于发生不完全故障的服务柜台，维修过程花费的时间是参数为ξ1的指数分布；对于发生完全故障的服务柜台，维修过程花费的时间是参数为ξ2的指数分布。假定顾客的等待过程、服务台的服务过程、不完全故障发生及维修过程、完全故障发生及维修过程全都相互独立。

(N(t),X(t))指系统中队列和服务柜台在时刻t的状态，N(t)指t时刻队列中的顾客数量，X(t)指t时刻服务柜台所处的不同状态，有

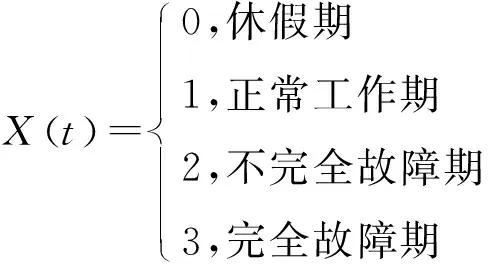
容易看出，(N(t),X(t),t≥0)在状态空间Ω={(n,0),n=0,1,…}∪{(n,1),n=1,2,…}∪{(n,2),n=0,1,…}∪{(n,3),n=1,2,…}上是一个连续时间马尔可夫过程。其中，(0,0)说明服务柜台处在休假期间，(0,2)说明服务柜台正在维修中。状态转移如图1所示。

图1 排队系统状态转移图

2 完全可见情形下的均衡策略分析

寻求服务的顾客在t时刻到达队列时，会被告知X(t)和N(t)。由于顾客的“故障厌恶性”，顾客在(n,2)，(n,3)时到达会立刻离开系统，不会进入排队，所以只需考虑顾客在(n,0)，(n,1)到达时的情况。假设此时有进队策略(ne(0),(ne(1))，顾客到达时若N(t)≤ne(X(t)),X(t)=0,1，则顾客会偏向于进入队列等待，否则偏向于离开。相应的系统状态空间为

Ωf={(n,0),n=0,1,…,ne(0)+1}∪

{(n,i),n=1,2,…,ne(1)+1,i=1,3}∪

{(n,2,n=0,1,…,ne(1)+1,}

状态转移图如图2所示：

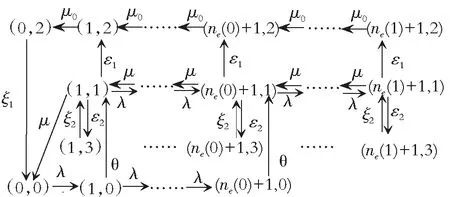
图2 完全可见时排队系统状态转移图

定理1当系统信息完全可见时，在具有延迟启动和两种故障类型的M/M/1队列中，有以下阈值：

(ne(0),ne(1))=(⎣xe(0)」,⎣xe(1)」)

依据此进队策略，若顾客在时刻t抵达队列，得知系统处于状态(N(t),X(t),X(t)=0,1)，若N(t)≤ne(X(t))，则选择进队，否则选择止步。其中⎣x」表示对x进行向下取整，xe(0)和xe(1)分别是以下两个方程的唯一解：

证明从系统中选取一个新抵达顾客，他抵达时得知系统处于状态(n,0)，(n,1)，且愿意进入队列，则由“获益-损失”函数可知，该顾客的预期收益为

S(n,i)=R-CT(n,i),i=0,1

(1)

其中，T(n,i)意为新抵达顾客获悉服务台所处状态为i,i=0,1时，从选择进入队列到离开系统所花费的平均逗留时间，R指顾客接受服务后获得的收益，C指顾客的单位时间等待成本。结合状态转移图2，可得：

(2)

(3)

(4)

(5)

(6)

注:T*(0,1)表示处于正常工作状态时，系统在服务完最后一个顾客的一瞬间有新顾客到达，此时系统还未关闭。

整理式(6)如下：

(7)

通过迭代式(7)，并结合T*(0,1)和T(1,1)，可知：

结合式(3)(4)和T(n,1)，得到：

整理可得：

T(n+1,1)-T(n,1)=

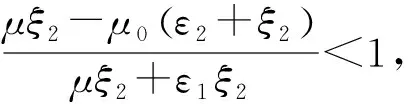
另外，始终假设在该系统中，S(0,0)≥0恒成立，即

以确保顾客在观察到系统状态为(0,0)时所得期望收益为非负，选择进入系统，否则系统不会被激活。定理1得证。

接着求系统的稳态分布。令p(n,i)∈Ωf表示系统各个状态的稳态概率，由图2得，系统稳态分布的平衡方程为

λp(0,0)=ξ1p(0,2)+μp(1,1)

(8)

(λ+θ)p(n,0)=λp(n-1,0)

n=1,2,…,ne(0)

(9)

θp(ne(0)+1,0)=λp(ne(0),0)

(10)

(μ+λ+ε1+ε2)p(1,1)=

μp(2,1)+ξ2p(1,3)+θp(1,0)

(11)

(μ+λ+ε1+ε2)p(n,1)=

λp(n-1,1)+μp(n+1,1)+ξ2p(n,3)+θp(n,0)

n=2,3,…,ne(0)+1

(12)

(μ+λ+ε1+ε2)p(n,1)=

λp(n-1,1)+μp(n+1,1)+ξ2p(n,3)

n=ne(0)+2,…,ne(1)

(13)

(μ+ε1+ε2)p(ne(1)+1,1)=

λp(ne(1),1)+ξ2p(ne(1)+1,3)

(14)

ξ2p(n,3)=ε2p(n,1),n=1,2,…,ne(1)+1

(15)

ξ1p(0,2)=μ0p(1,2)

(16)

μ0p(n,2)=

μ0p(n+1,2)+ε1p(n,1),n=1,2,…,ne(1)

(17)

μ0p(ne(1)+1,2)=ε1p(ne(1)+1,1)

(18)

定理2 在排队系统信息完全可见条件下，对于带有启动时间和两类故障类型的服务系统，若所有顾客皆采取阈值策略(ne(0),ne(1))，则系统各状态平稳分布为

p(n,0)=σnM,n=0,1,…,ne(0)

n=1,2,…,ne(0)+1

n=ne(0)+2,…,ne(1)+1

n=1,2,…,ne(1)+1

n=ne(0)+2,ne(0)+3,…,ne(1)+1

其中，

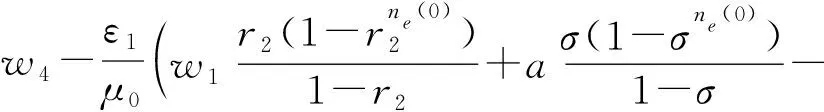
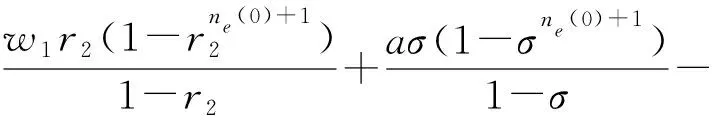
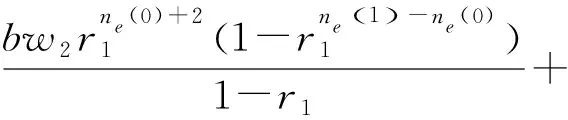
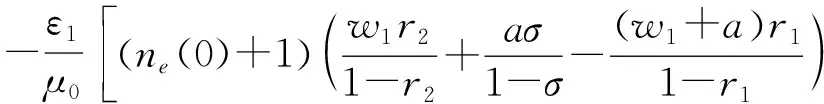
v6=w3+(ne(0)+1)w4+(ne(1)-ne(0))w5+v4+v5

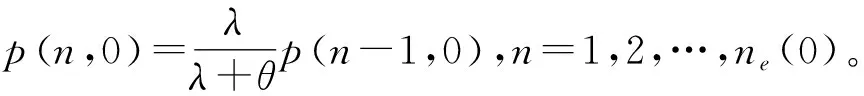
结合式(12)(15)，可得(μ+λ+ε1)p(n,1)=λp(n-1,1)+μp(n+1,1)+θσnM,n=2,3,…,ne(0)，即p(n,1),n=1,2,…,ne(0)+1是常系数差分方程：

μxn+1-(μ+λ+ε1)xn+λxn-1=-θσnM

n=2,3,…,ne(0)

(19)

的解，对应的特征方程为μx2-(μ+λ+ε1)x+λ=0，方程有两个实根：

μxn+1-(μ+λ+ε1)xn+λxn-1=0,

n=ne(0)+2,…,ne(1)

(20)

的解。对应的特征方程为μx2-(μ+λ+ε1)x+λ=0，方程有两个实根：

为求出B1和B2，需要先解出p(ne(0)+2,1)。所以将已经解出的p(ne(0)+1,1)和p(ne(0),1)代入式(12)，解出p(ne(0)+2,1)=cB1+dM。所以可以通过联立p(ne(0)+2,1)和p(ne(0)+1,1)，解出B1=w1M，B2=w2M，即可解出p(n,1),n=1,2,…,ne(1)+1。

将p(1,1)代入式(8)，得到p(0,2)=w3M。由式(16)，得出p(1,2)=w4M。化简式(17)，可得

(21)

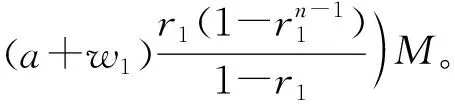
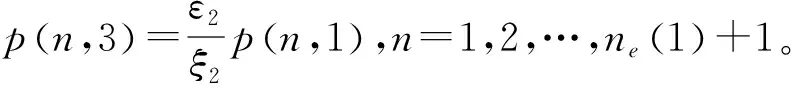
最后，利用归一化条件：

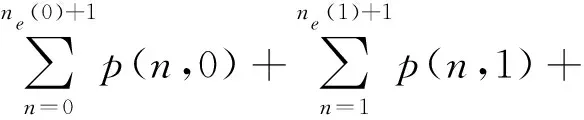
得到所有状态的稳态分布概率，从而定理2得证。

当所有顾客都遵循阈值策略(ne(0),ne(1))时，系统的平均队长为

顾客的有效进队率为

从而得到系统的平均社会收益为S=λeR-CE(N)。

3 数值模拟

考虑部分主要系统及服务参数对于阈值策略和社会预期收益的影响，通过具体的数值模拟分析它们关于参数的敏感性。首先，给出进队阈值ne(0)关于启动时间θ和服务速率μ的变化趋势。先给定系统中的几个基础参数，由定理1可得ne(0)与ξ1和λ无关。给定以下参数的值：R=14，C=1，μ0=1，ξ2=0.2，ε1=0.2，ε2=0.2。由图3可知进队阈值随着μ的变大，整体走势是上升的，且随着θ的逐渐变大，进队阈值整体上移，但上升的幅度逐渐变小，说明θ的影响在变小。由此得出，减少启动时间和增大服务速率可以让更多数量的顾客愿意进入队列。接下来研究故障发生率ε1和ε2对进队阈值ne(1)的影响。令R=14，C=1，μ=2，μ0=1，ξ1=0.2，ξ2=0.2。从图4可以看出，当0.1≤ε2≤0.4时，曲线整体下移，但不会低于13；当0.7≤ε2≤1.4时，曲线整体上移，但不会高于12。这说明随着ε1的增大，其对于进队阈值的影响逐渐减小；随着ε2的增大，曲线呈现两种完全不同的变化趋势，分水岭出现在ε2在0.4～0.7之间。可以预见曲线在0.4～0.7之间应该是水平的线，这也说明了ε1和ε2之间会互相影响。

考虑社会平均收益关于ε1和ε2的敏感性。令R=14，C=1，μ=2，μ0=1，ξ1=0.3，ξ2=0.3，θ=0.8。从图5可得社会平均收益随着ε1的增加而减小，且曲线之间的差距慢慢变小；随着ε2的增大而减小，且曲线逐渐变得平缓。这说明不管任何一种故障出现速率变大，社会平均收益均会降低。最后讨论社会平均收益关于ξ1和ξ2的敏感性。令R=14，C=1，μ=2，μ0=1，ε1=0.3，ε2=0.3，θ=0.8。从图6可得，社会平均收益随着ξ2的增大而上升，且曲线慢慢变得平缓；随着ξ1的增大而上升，且曲线之间的差距在慢慢变小。这说明系统中提升故障维修率获得的收益逐渐减小，所以当维修率到达一定程度时，从提高维修率的角度去提升社会平均收益不经济。

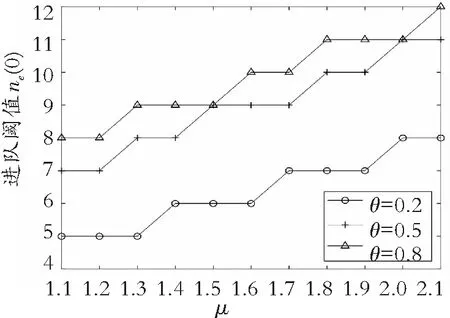
图3 进队阈值ne(0)随θ和μ的变化趋势

图4 进队阈值ne(1)随ε1和ε2的变化趋势

图6 社会平均收益随ξ1和ξ2的变化趋势

4 总 结

当队列人数和服务柜台工作状态都可知时，在具有两种不同故障类型的M/M/1排队系统中，对于采取延迟启动休假策略的服务台，得到了顾客的进队阈值以及社会预期收益表达式；对于感兴趣或实际可调节的参数，结合具体的数值模拟，分析了其对顾客的进队决策和预期社会收益的影响，为社会生产和日常生活中相应的服务系统控制提供理论依据。