子母弹内燃式金属气囊抛撒中流固耦合作用特性研究
2022-04-08周双利陶如意
周双利,王 浩,陶如意
(南京理工大学 能源与动力工程学院,南京 210094)
1 引言
作为一种应用了多种现代高新技术的复杂武器系统,子母弹战斗部的作用过程十分复杂,其中涉及子弹的抛撒、子弹与母弹的分离、子弹的自由飞行等过程,且无论对于哪种类型的子母弹,子弹药的抛撒、分离技术无疑是研制过程的重中之重。尤其对于超音速飞行的子母弹,子弹分离过程中必须穿过母弹和其他子弹形成的弹头激波。在复杂的母弹和子弹、子弹和子弹相互干扰的激波流场中,要求子弹具有一定的抛撒速度,以及翻转角速度和姿态角才能安全与母弹分离,同时子弹的翻转也会对子弹的外弹道,尤其是初始外弹道阶段及减速段减速伞的打开和气动特性产生较大的影响,进而影响子弹动作的可靠性和子弹分布的合理性。因此研究子弹抛撒方式的选择、抛撒内弹道特性以及弹道控制技术,对于提升导弹子母弹的可靠性和抛撒精度至关重要。
内燃式气囊抛撒结构是一种结构简单、易于设计和操作的子母弹子弹抛撒方式,具有较为广泛的应用前景。其中,子母弹金属波纹管抛撒以其抛撒行程长、分离速度快、强度高等优点在子母弹战斗部得到了广泛的应用。图1为内燃式气囊抛撒的示意图。
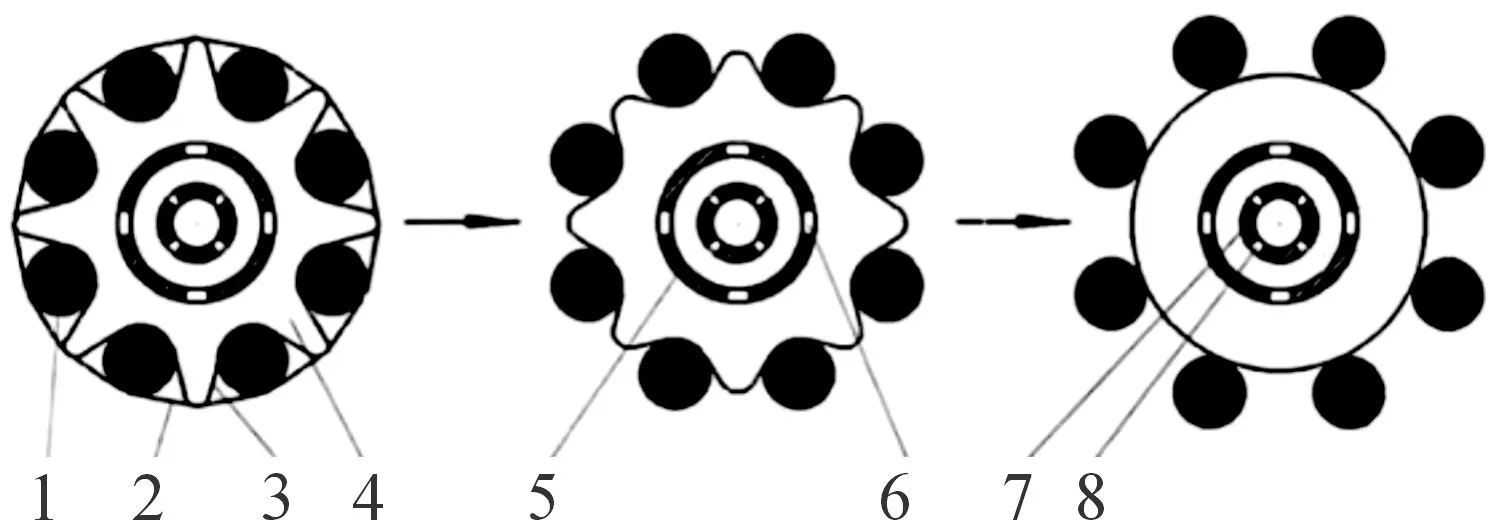
1-子弹;2-弹箍;3-气囊;4-腔体;5-中心管;6-下孔;7-点传火管;8-传火孔图1 内燃式气囊抛撒原理示意图
波纹管式金属气囊的膨胀过程是一个典型的双向耦合、强非线性过程,以往文献中通常采用实验和内弹道模型来辅助设计和预测分离结果,以了解金属波纹管变形的动态特性和波纹管变形的变化规律。本文建立了一个内部流场流固耦合(fluid-structure interaction,FSI)模型来模拟这种扩散过程,并用FSI方法和任意拉格朗日-欧拉(arbitrary lagrange-euler,ALE)算法分析了这种FSI问题的特点。
实际上,之前的研究都是从研究低速流作用下柔性薄膜的变形入手的,而对于金属波纹管在气体压力作用下,由于薄膜应力和弯曲应力的作用而发生较大变形的FSI问题却鲜有研究。本文介绍了一种计算粘性可压缩流与大变形结构相互作用的FSI方法,并针对这种方法利用ADINA软件模拟了金属波纹管膨胀抛撒子弹。在拉格朗日和ALE公式中,结构方程和流动方程分别用Galerkin方法和Petrov-Galerkin方法进行离散。然后采用迭代法求解2组方程,得到金属波纹管变形的动态特性、内部流场的变化规律和炸弹的运动规律。
2 流固耦合控制方程
2.1 流体域
气囊的膨胀是含运动边界的非稳态过程,流体域的任意拉格朗日-欧拉描述(ALE描述)为:
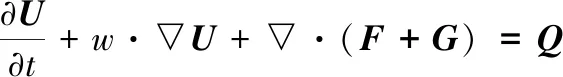
(1)
=(-)
(2)
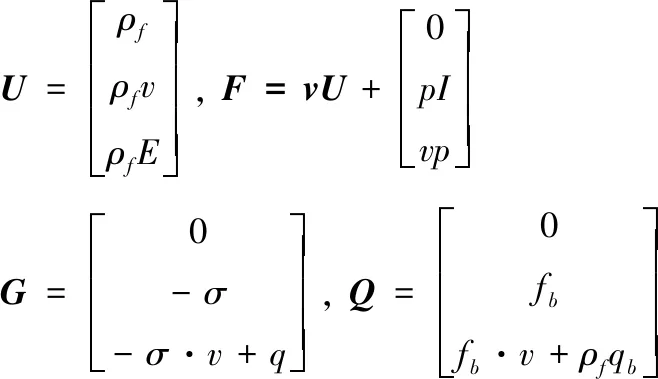
(3)
根据假设(1),对文献中描述的内弹道方程进行计算,然后将气体发生器内弹道参数应用于流体方程的边界条件。

(4)
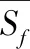
采用基于Petrov-Galerkin变分法的基于流动条件的插值法(flow-condition-basd-interpolation,FCBI)单元法对方程(1)~(4)进行如下离散,即:
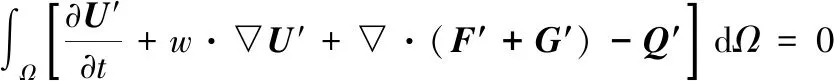
(5)
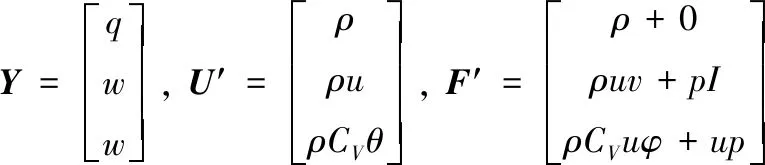
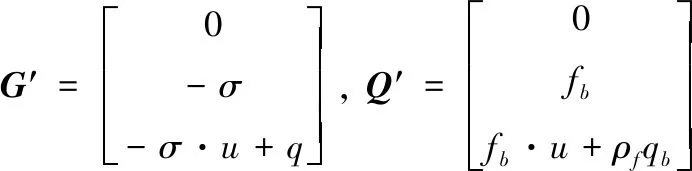
在FCBI单元算法中,用Galerkin法建立了非对流项的插值函数,并基于局部雷诺数(速度)和派克叶数(温度)来建立权函数,以此来避免高雷诺数和高派克数引起的对流项的不稳定性。
2.2 结构域
材料模型为双线性本构模型。结构域的平衡方程由拉格朗日公式确定,即:
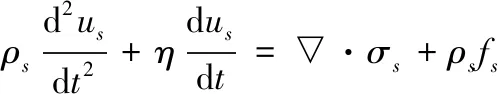
(6)
=ε
(7)
=-
(8)
式(6)中:为结构的位移;为结构密度;为阻尼系数;为结构上单位体积受的体力。
根据假设(2),应力张量和应变张量之间的关系由式(7)和弹性矩阵给出。和分别为时刻主、从接触点的受力。
2.3 流固耦合动态迭代法
流体的运动平衡条件和运动结构条件是界面的动力学条件,即:
=,=
(9)
式(9)中:、分别为流固耦合边界上的位移和应力;下标、分别对应流体域和结构域。
将流体域和结构域对应的解向量定义为f和S,因此流固耦合问题的耦合方程可以简写为:
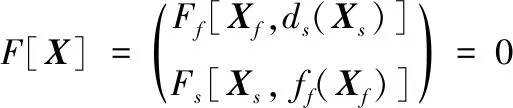
(10)
采用Euler法对耦合方程进行时间积分,然后将结果应用到整个计算域中,在每个时间步内进行Newton-Raphson迭代,直到解收敛为止。
2.4 网格重构方法
由于气囊膨胀过程,气囊会发生大位移,气囊腔体内的流体域网格会被过度拉伸,网格质量变差,从而导致下一步的求解无法收敛。本文引入一种网格重构法来对网格进行重划分,网格重构法的原理是将旧网格上流场的信息传递到新网格上,只保留新网格来继续进行求解。捕捉获得变化的流场信息,基于压力梯度和涡量的判定准则对流体域进行网格重构。
梯度准则的表达式为:

(11)
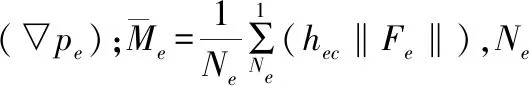
计算域内所有网格的尺寸都可表示为:
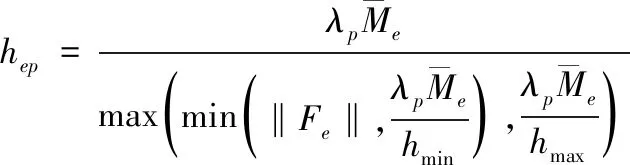
(12)
式(12)中,和分别为计算域内最小与最大尺寸。
3 抛撒过程的流固耦合分析
3.1 有限元模型
计算域网格的划分
流体域如图2(a)所示,采用四面体单元网格,网格数为747 963,采用瞬态分析,结构域如图2(b)所示,囊壁为304不锈钢,采用双线性弹塑性本构描述,厚度为1 mm,采用面网格,结构域总网格数为50 277,采用隐式动力学求解。求解域的物性参数如表1所示。
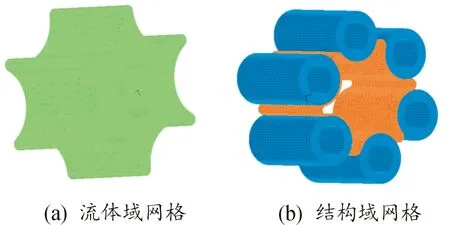
图2 抛撒有限元模型示意图
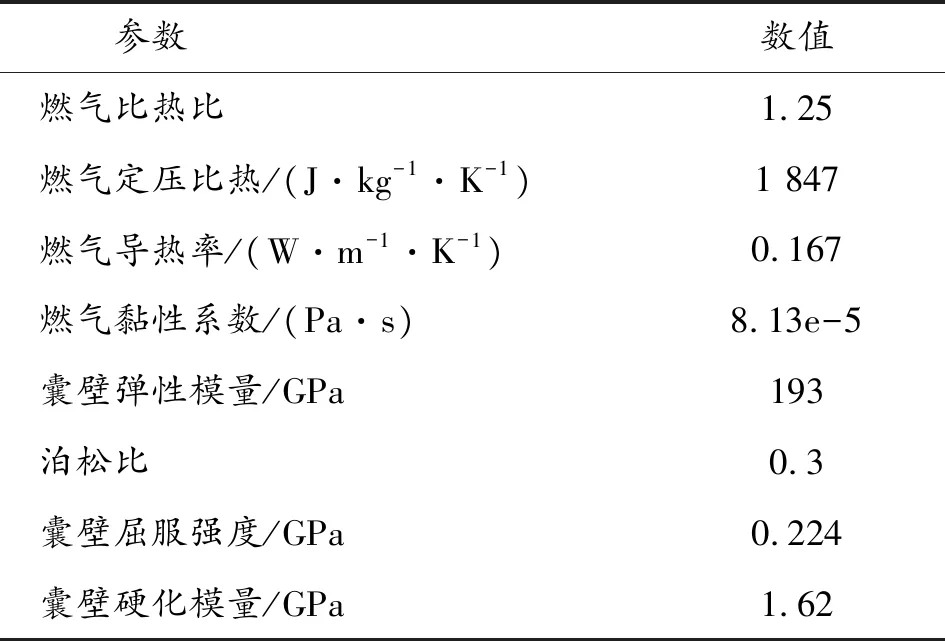
表1 内燃式金属气囊抛撒系统的材料参数
入口边界条件
本文中的内燃式气囊抛撒的内弹道过程主要分为3个过程:定容燃烧(中心管薄膜破裂前),气囊定容充气(中心管薄膜破裂到弹箍断裂前),子弹开始运动到子弹脱离气囊。图3为内弹道仿真得到的中心管内压力、温度和气囊内压力曲线。本文以内弹道仿真得到的温度和压力作为子弹抛撒过程流固耦合仿真的入口条件,由气囊内压力随时间变化曲线可知,中心管破膜大约发生在4.72 ms,因此将内弹道过程的4.72 ms作为流固耦合仿真的零时刻,得到的入口边界条件如图4所示。

图3 内弹道仿真曲线
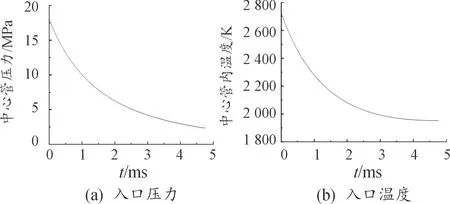
图4 入口边界条件曲线
3.2 计算结果分析
囊内的流场分析
采用上述流固耦合模型计算得到了各个时刻金属气囊的内部流场,典型时刻的压力分布如图5所示,不同时刻金属气囊内速度矢量变化如图6所示,不同时刻气囊径向轴线上压力的变化如图7所示。压力单位为MPa。整个过程大致可分为3个阶段。
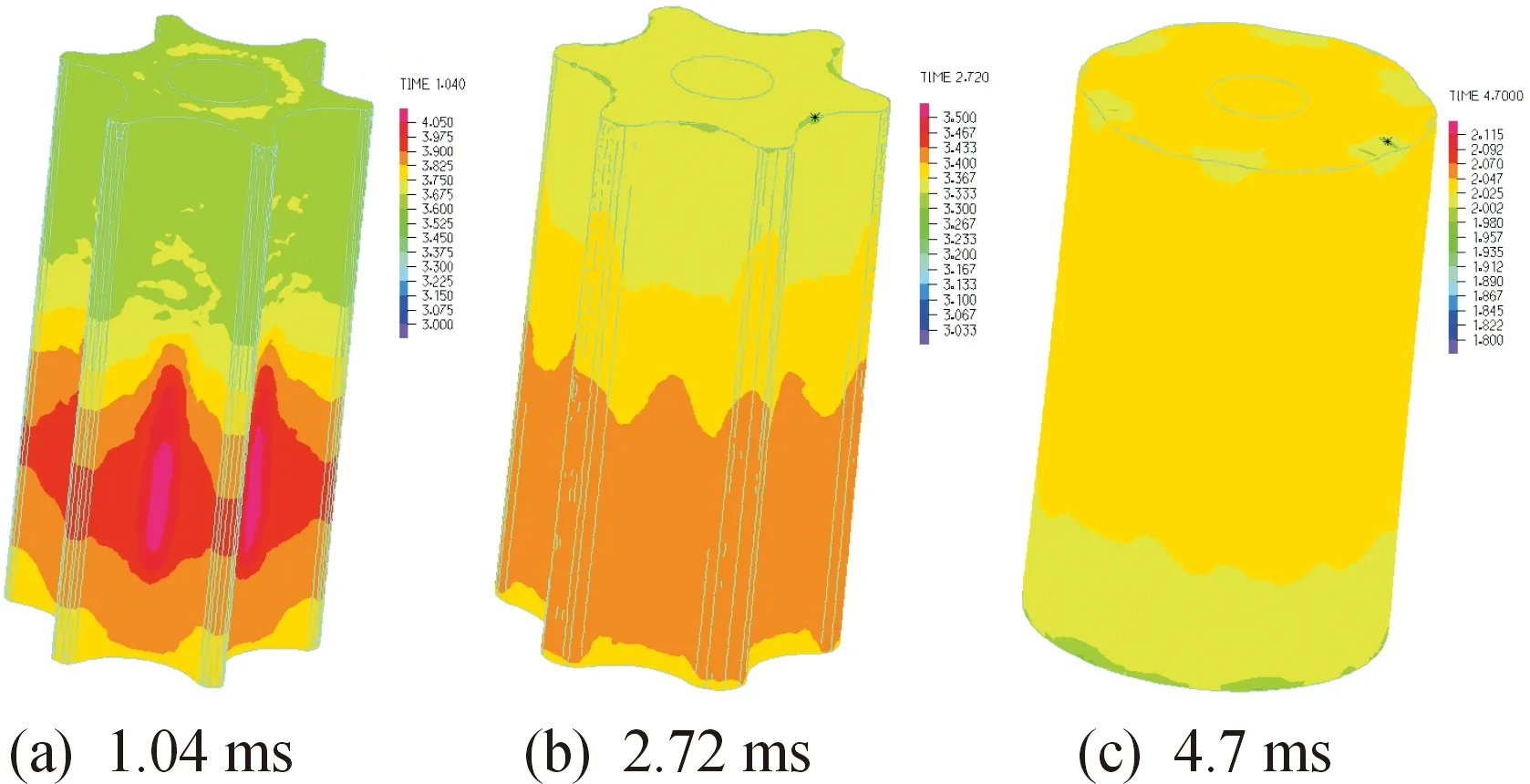
图5 不同时刻金属气囊内流场压力云图
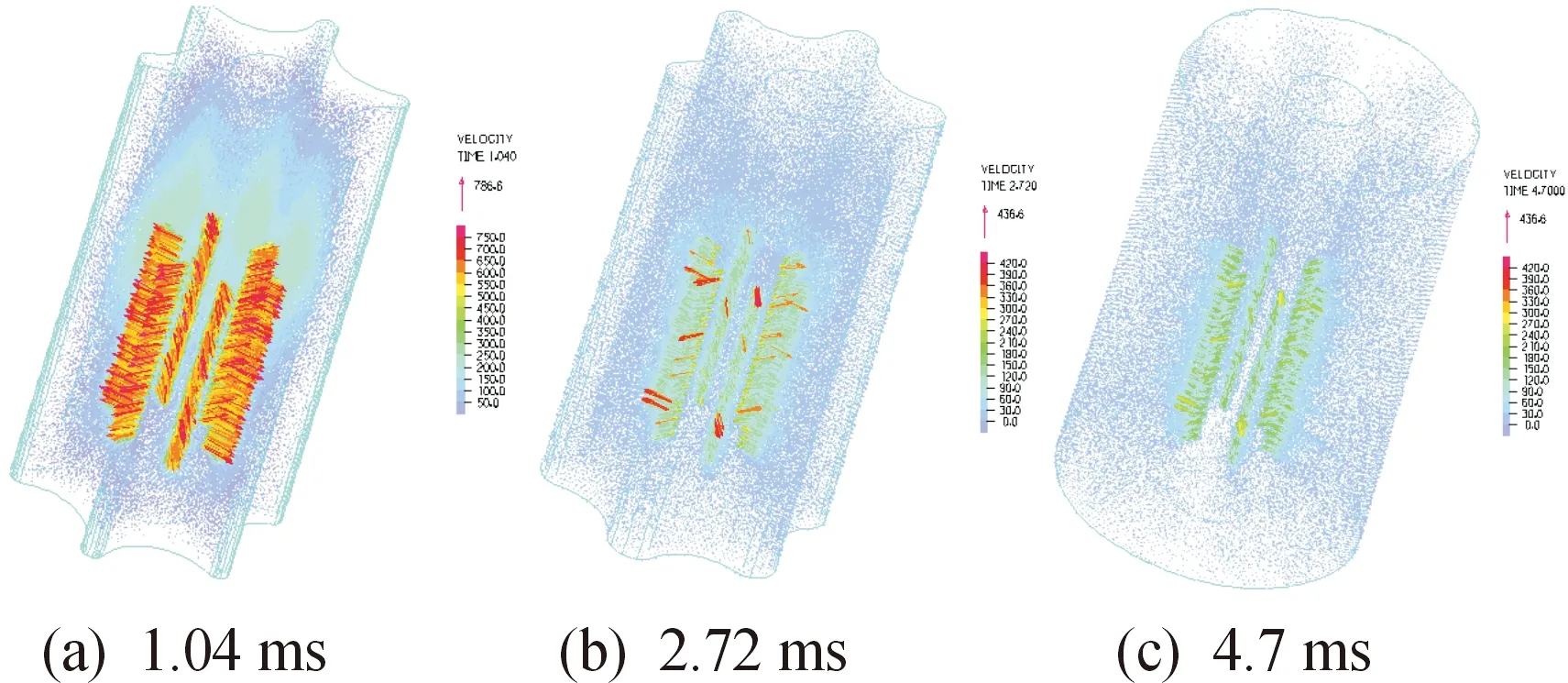
图6 不同时刻金属气囊内速度矢量云图

图7 不同时刻气囊径向轴线上压力的变化
1)定容充压阶段。高温高压的气体通过中心管小孔以局部音速流入气囊内部,由于初始时刻腔体内的压力较低,流体由中心管喷孔向气囊内部喷射的范围较广,腔体内压力急剧上升,但由于金属气囊的刚性和子弹外部弹箍的作用,使得腔体内容积变化很小,近似于定容充气,因此气囊并未开始膨胀。
2)充气膨胀阶段。这个阶段发生在弹箍断裂之后,气囊开始膨胀,金属气囊的应力与应变迅速增加,气囊内压力经历先增大后逐渐下降的变化过程,压力梯度也逐渐趋于平缓。
3)充气后期阶段。这个阶段,随着气囊内腔体逐渐增大,流体的压力继续变小直至趋于稳定,应变代替几何变形成为主要的变形模式,这一阶段结束于子弹以最大速度与气囊分离的那一刻。
从图5中可以看出,气囊内部压力随时间增加总体上是减小的,图7为不同时刻气囊的波谷位置处径向轴线上压力的变化,图7中显示,气囊在入口处的压力比较高,并往气囊膨胀的方向递减,气囊在充气膨胀阶段,内部腔体的压力都比较均匀。结合图6可以看出,随着气囊的进一步膨胀,入口处压力与气囊内部压力的压差逐渐减小,囊内气体的流动逐渐变缓,流场趋于稳定。
囊壁应力分析
图8为囊壁上应力分布图,由于入口中心管小孔的偏置,在膨胀后期,气囊有另一边并未完全展开,子弹与气囊分离时也具有一定的攻角,在气囊未完全展开的一边存在一些高应力区和低应力区。总体来看,囊壁的应力在原波峰处为最低,逐渐向两边递增。
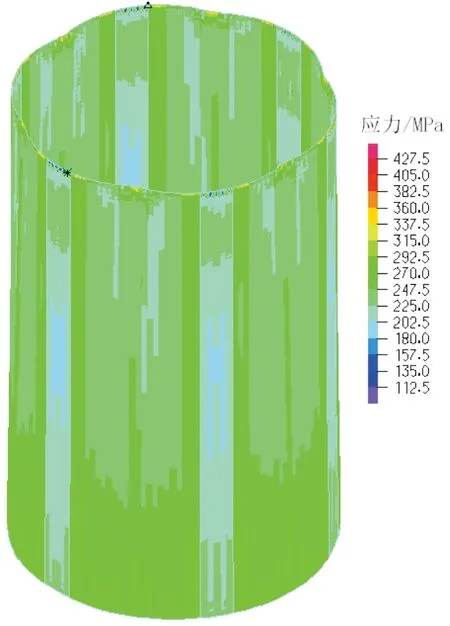
图8 囊壁的应力分布云图
在金属气囊上选取3个点来监测气囊不同位置处的应力变化情况,如图9所示。
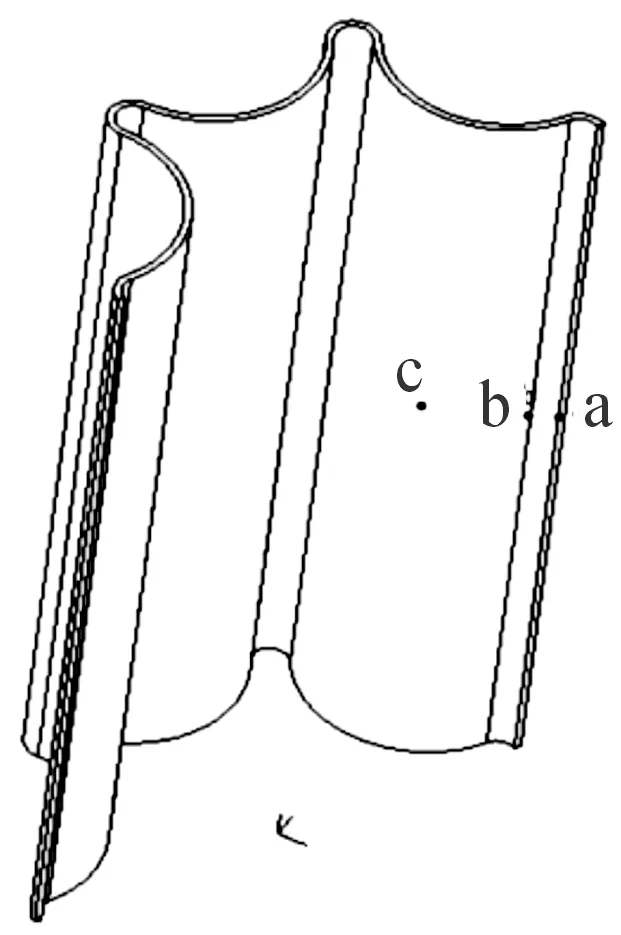
图9 二分之一气囊示意图
图10为囊壁上的应力分布曲线,显示的应力主要在波峰(a点)、波谷(c点)以及他们的连接处(b点)的位置,应力随时间总体上呈增长的趋势。由于受到弹箍的影响(0.3 ms前),子弹位移很小,c点的应力变化很小,直到第二阶段结束。在弹箍约束解除后,子弹加速抛出,破坏了气囊原本存在接触力约束的应力平衡,因此应力均迅速上升,随着子弹与气囊接触面积的减小,a点受气囊接触力的影响变弱,应力主要受囊内压力大小决定,由于此时囊内压力降低较快,因此应力也在减小,在气囊达到一定位移后,此处应变逐渐代替几何变形,成为主要变形模式,应变的增加又使得该处应力值增大,在膨胀后期,气囊在a点处的结构趋于稳定,a点处应力又开始降低。b点在初始时刻受压力的影响收紧,气囊的弯曲使b点处的拉应力变成压应力,b点向波谷处移动,因此在1.32 ms时b点应力开始减小,由于子弹的运动和气囊的位移,子弹的惯性对气囊的几何约束减小,其应力恢复为拉应力,应力又开始上升。在子弹与气囊分离时刻,a点处应力最小,c点处应力最大。
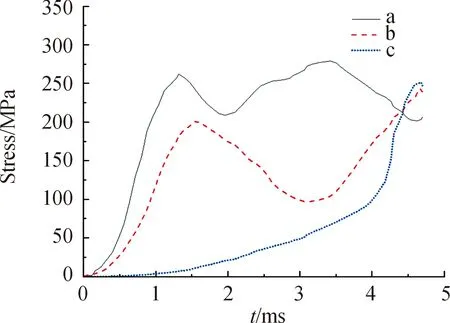
图10 气囊壁上不同部位应力分布曲线
图11和图12为子弹抛撒过程中的加速度和速度曲线。
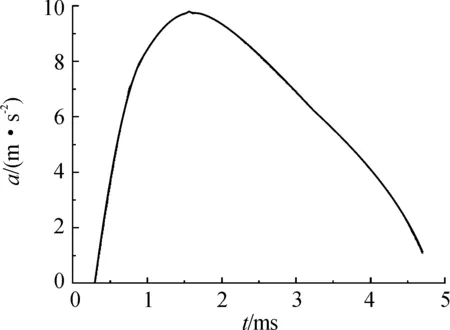
图11 子弹加速度曲线

图12 子弹速度曲线
可见流固耦合模拟和实验得到的子弹抛速是很接近的,如表2所示,由此验证了本文建立的流固耦合模型的正确性和结果的准确性。

表2 计算结果与实验结果
4 结论
本文根据波纹管式金属气囊抛撒过程中流固耦合的特点,介绍了一种计算粘性可压缩流与大变形结构相互作用的流固耦合动态迭代法,并对金属波纹管抛撒三维动力学模型进行了仿真,得出以下结论:
1)该模型的计算结果显示了气囊内流场经历的定容充压、充气膨胀、充气后期3个阶段。对腔体内流体的压力变化进行了分析,发现随着气囊逐渐膨胀,腔体内的压力逐渐降低。
2)该流固耦合数值仿真得到了金属气囊膨胀过程中不同位置的应力变化情况,得到了波纹管式金属气囊最大应力的时刻和位置,为工程设计提供了有效的理论依据和参考。
3)本文得到了子弹加速度和速度随时间的变化曲线,模拟得到的弹丸抛速与实验的抛速基本吻合,验证了模型的合理性和抛撒结果的准确性。
