基于改进粒子群的食品分拣机器人动态目标抓取控制方法

王 敏 蒋金伟 曹彦陶

(1. 安徽科技贸易学校，安徽 蚌埠 233080；2. 常州工业职业技术学院，江苏 常州 213164；3. 江苏大学，江苏 镇江 212013)

随着工业4.0的兴起和互联网浪潮席卷全球，各国都将制造业的转型升级作为重点，提高制造业和自动化水平是大势所趋[1]。机器人是自动化时代的象征，是智能时代的基石。以工业机器人技术为代表的智能生产线越来越受到重视[2]。Delta机器人具有刚度高、运动速度快、负重比高等优点，在食品、医药等轻工业中被广泛应用。但在实际应用中，Delta机器人在食品分拣中存在运动不稳定、分拣效率低等问题。

目前，国内外许多学者对食品分拣机器人控制方法进行了研究，尝试将智能控制算法用于抓取控制，提高系统鲁棒性，主要包括粒子群算法、蚁群算法、遗传算法等控制方法。倪鹤鹏等[3]提出了一种将牛顿迭代法用于机器人抓取控制。建立跟踪模型，通过牛顿迭代法进行求解。结果表明，该方法的最快分选速度为1.5次/s，误抓取率为0.2%，漏抓率为0，具有较高的精度和稳定性。郝琳等[4]提出了一种将模糊神经网络与改进粒子群优化算法相结合的控制方法。结果表明，该系统具有较低的误抓取率和漏抓率，控制在0.1%以内，抓取精度高，能够满足食品包装的要求。郝大孝等[5]提出了一种用于Delta机器人的动态抓取算法，完美融合机械视觉和抓取方法。结果表明，在目标排序和跟踪过程中，Delta机器人的漏检率控制在2%以内，误检率为0。郭俊等[6]针对三自由度并联机器人在食物取放作业中运动不稳的问题，提出了以最优运动时间为目标的回转与圆弧相结合的方法，并利用蚁群算法得到运动轨迹参数。结果表明，该方法能够提高分拣机器人的稳定性和分拣效率，减小了末端执行器的抖动。上述方法可以满足高速食品分拣机器人的一般要求，但在分拣操作中存在运行不稳定、分拣效率低等问题，有一定的局限性，适应性有待进一步提高。

针对食品分拣机器人抓取运动不稳定、分拣效率低等问题，提出了一种基于改进粒子群(Particle Swarm Optimization，PSO)算法的多目标运动优化策略用于食品分拣机器人的动态目标抓取控制。目前粒子群算法的改进方法众多，但是大部分都较为复杂，而目标抓取需要快速性，因此，通过两个方面对其进行改进，改进惯性权重利于跳出局部极值，改进学习因子提高全局最优解的精度。协调抓取顺序和分拣轨迹建立最短路径模型，以末端加速度建立机构稳定性优化模型，并通过改进粒子群优化算法对目标进行优化，以期为分拣机器人控制技术的发展提供依据。

1 分拣机器人结构

图1为高速并行食品分拣机器人的系统结构。高速并联食品分拣机器人系统主要由上位机系统和下位机系统组成。其中，下位机控制系统是Delta机器人的核心指令部分[7]。其主要功能是驱动机器人主体以稳定、协调、快速的方式完成既定的运动规划和抓取任务，满足工作要求。上位机系统其主要功能是可视化、模型分析、数据集成处理以及与下位机的信息交互。

图1 系统结构Figure 1 System structure

食品分拣机器模型人主要由7个部分组成：静(动)平台、主(从)动臂、伺服电阻、减速器、末端执行器[8]。伺服电机安装在静平台，末端执行器安装在动平台。静、动平台之间通过运动链连接。从动臂由4个球铰组成闭环平行四边形。闭环与驱动臂刚性连接，驱动臂通过旋转副与静平台连接。机器人通过平行四边形对动平台的运动方向进行约束，使静、动平台保持平行。

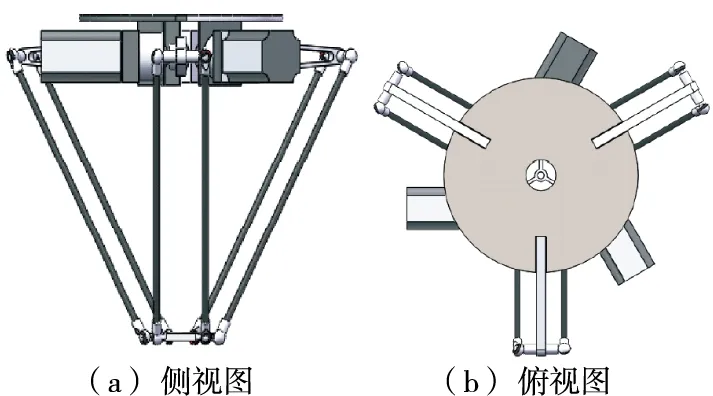
图2 食品分拣机器人模型Figure 2 Food sorting robot model

2 动态目标抓取控制方法

现有的研究大多集中在单路径优化上，不能从整体上提高分拣效率[9]。文中提出了一种基于改进粒子群的多目标动态优化算法用于抓取控制。

2.1 改进粒子群算法

粒子群的机制是一种基于蜜蜂、蚂蚁和鸟类习惯的搜索算法[10]。个体遵循不碰撞的规则，个体速度匹配，个体朝着共同的目标前进。相比于遗传算法、模拟退火算法、蚁群算法，粒子群算法规则更为简单、收敛速度快、计算时间短等。它适用于动态多目标优化，在机器人控制、交通运输等领域应用较为广泛。简言之，在粒子群优化算法中，粒子通过目标函数确定适应值，由速度来确定其飞行方向和距离，剩余粒子根据当前最优粒子搜索解空间[11]。粒子通过多次迭代得到最优解。在迭代过程中，粒子跟踪极值并更新粒子本身。一种是个体极值，粒子本身检测到的最优解。一种是全局极值，即剩余粒子群检测到的最优解。

迭代之后，在所有粒子的最优解之后，对速度和位置进行更新，如式(1)和式(2)所示[12]。

vid=ωvid+c1r1(pbest-xid)+c2r2(gbest-xid)，

(1)

xid=xid+mvid，

(2)

式中：

c1、c2——自学习和社会学习的因子；

xid——d维数第i个粒子的位置；

vid——d维数第i个粒子的速度，mm/s；

ω——惯性的权重；

r1、r2——随机数；

m——约束因子，通常为1。

但粒子群算法也存在早熟收敛、局部寻优能力差、易陷入局部极值等缺点，因此，文中通过两个方面对其进行改进，改进惯性权重利于跳出局部极值，改进学习因子提高全局最优解的精度。

2.1.1 惯性权重的改进 惯性权重越小局部搜索越有利，越大全局搜索越有利。随着迭代次数的增加，问题的求解细节也随之增加，固定值求解存在着许多缺陷。因此，引入可变惯性权重，通过式(3)进行动态惯性权重调整[13]。

(3)

式中：

λ——经过迭代测试后可以得到的权重因子(值为0.01优化效果最好)；

N——粒子数；

t——当前粒子迭代次数；

pbest,i(t)——当前个体最优值；

gbest——当前全局最优。

2.1.2 学习因子的改进 采用对学习因子进行线性递减和线性递加的策略。可以在搜索前期增强全局搜索，使之不易陷入局部最优，而在搜索后期增强局部搜索能力，提高全局最优解的精度，具体方程如式(4)和式(5)所示[14]。

(4)

(5)

式中：

tm——最大迭代次数；

c1max、c2max——最大学习因子；

c1min、c2min——最小学习因子；

t——粒子当前的迭代次数。

算法步骤：

步骤1：初始化。对粒子数、迭代次数等进行初始化[15]。

步骤2：计算每个粒子的目标函数，求解全局最优解和个体最优解。

步骤3：对粒子位置和速度进行更新。

步骤4：确定是否达到停止条件。达到输出最优解，未达到转到步骤2。改进算法的流程图如图3所示。

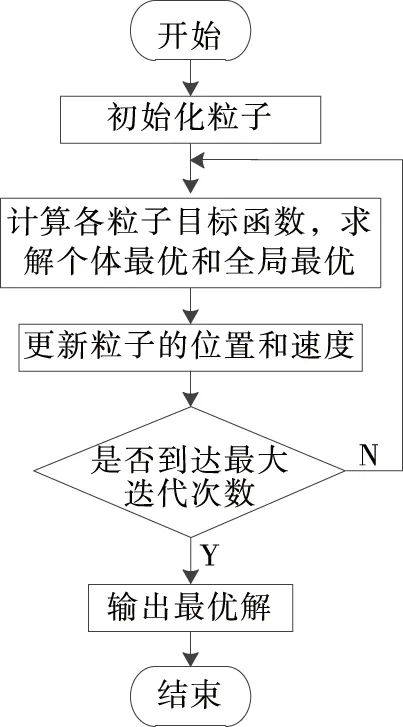
图3 改进粒子群算法的优化流程Figure 3 Optimization process of improved particle swarm algorithm

2.2 最短抓取路径模型

在食品生产中，需要对机器人抓取策略进行优化，以提高机构分拣效率。通过调整抓取食品的顺序和分拣路径，可以提高工作效率[16]。最短路径模型的建立过程是：将食品放置在传送带上的同一水平线上，z方向上的坐标相同。为了方便计算，将其设置为0。将食物放置在(x0,y0,0)。传送带上第i个食物的位置是(xi,yi,0)。传送带沿x轴的速度设置为v，从第i个食品到第j个食品的抓取时间为ti，最短抓取路径模型如式(6)所示[17]。

(6)

式中：

Sij——末端从i到j的抓取路径，其计算如式(7)所示。

(7)

Xij为决策变量，决定从食品i到食品j的路径是否执行，如式(8)所示[18]。

(8)

2.3 平稳性模型

机器人抓取中的稳定性较低，容易产生振动或冲击，以末端加速度建立机构稳定性优化模型，如式(9)所示[19]。

(9)

式中：

aij——末端从i到j的加速度，mm/s2。

其次，需要对末端的速度和加速度进行限值。即aij1,aij2≤amax，vij1,vij2≤vmax，为防止机器人反复抓取食品，需要i≠j。

2.4 多目标优化算法

综合2.2和2.3的模型建立目标函数，如式(10)所示[20]。

minf(x)={f1(x),f2(x)}，

(10)

式中：

minf1(x)=S；

minf2(x)=a。

通过改进的粒子群算法对多目标问题进行优化，将两个目标作为权重w∶1(两个目标占比)的优化目标，文中w=1，如式(11)所示[21]。

(11)

多目标优化算法的步骤：

步骤1：初始化。对粒子数、迭代次数等进行初始化。

步骤2：获取机器人相关参数和目标食品的位置等。

步骤3：对模型进行计算，更新粒子速度和位置。

步骤4：对是否为最优解进行判断。如果满足该标准，则输出最优解。如果不符合标准，则转到步骤3。图4为多目标优化算法的流程。

图4 多目标优化算法流程Figure 4 Algorithm flow of Multi-objective optimization

3 结果与分析

3.1 仿真分析

为了验证多目标优化方法的性能，仿真设备为联想PC，操作系统为windows10 64位旗舰版，intel i5 2450M CPU，频率2.5 GHz，matlab r2018a为仿真平台。采用平均分布方式，每次识别的食品数设置为10个。文中优化权重w=1，分布范围为[-400,+400] mm，传输速度为100 mm/s。粒子数为100，最大迭代次数为100，为了保证模拟结果的准确性，文中选取了两种分布密度(100，150个/min)进行验证。

分拣机器人在优化前抓取都是按照坐标顺序进行，优化后是多目标优化，不同分布密度(100，150个/min)下的抓取分布图如图5所示。

由图5可知，在不同分布密度(100，150个/min)下，优化后抓取分布图更加集中，工作区间也明显缩短。验证了文中多目标优化算法的有效性，该算法可以在一定程度上提高系统的抓取稳定性和分拣效率。

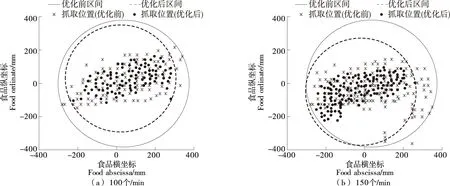
图5 不同分布密度的多目标优化前后抓取分布图Figure 5 Grab distribution map before and after multi-objective optimization with different distribution density

3.2 试验分析

通过分拣平台对文中方法在抓取稳定性和分拣效率方面的性能进行实验验证，为了尽可能地接近真实工况，将相机拍摄频率设置为100帧。传送速度分别设置为100，200 mm/s。末端的最大速度和最大加速度分别为Vm=4 m/s、am=300 m/s2，进行以下分析。

3.2.1 抓取成功率 通过实际抓取试验对改进前后抓取的成功率进行对比分析，目标食品500个，确保每次试验传送带上的食品种类数、分布密度、抓取速度等相同。利用3种分拣操作方法(不采用POS优化、POS优化、改进POS优化)，进行多次试验取平均值，结果见表1。

表1 3种抓取策略的结果对比Table 1 Comparison of capture results of different capture strategies

由表1可以看出，在相同的食品输送速度下，改进PSO优化控制抓取成功率最高，随着输送速度的增加，3种控制的抓取成功率都有一定程度的下降。不采用PSO优化控制从96.8%降低到94.2%，采用PSO优化控制从98.6%降低到98.2%，改进PSO优化控制从100.0%降低到99.8%。说明文中提出的方法在准确性、稳定性和分拣效率方面都有所提高。

3.2.2 分拣效率 在输送速度100 mm/s时，使物体分布密度相同。记录抓取500个食品的总时间，重复30次。根据试验数据，计算不采用粒子群优化控制、采用粒子群优化控制、采用改进粒子群优化控制策略抓取速率的平均值，结果如表2所示。

由表2可知，在相同带速下，文中提出的优化策略平均抓取效率最高，在一定程度上提高了分拣作业的工作效率。

表2 不同抓取策略抓取速率对比Table 2 Comparison of grab rates with different grab strategies

3.2.3 算法对比 在输送速度100 mm/s时，使物体分布密度相同。采用改进粒子群优化控制策略和文献[3]中基于牛顿-拉夫森迭代的动态抓取策略进行抓取试验，记录抓取500个食品的总时间和抓取成功率，重复30次取平均值，结果如表3所示。

表3 改进粒子群优化和牛顿-拉夫森迭代动态抓取策略的对比Table 3 Comparison between improved particle swarm optimization and Newton Raphson iterative dynamic grasping strategy

由表3可知，在相同带速下，文中改进PSO优化控制方法在抓取速率和抓取成功率方面都优于文献[3]牛顿—拉夫森迭代。通过对比试验数据分析，文中提出的方法不仅提高了抓取成功率，而且降低了抓取时间，实现了提高分拣效率的目的。

4 结论

文中提出了一种基于改进粒子群算法的多目标运动优化策略用于食品分拣机器人的动态目标抓取控制方法。以协调抓取顺序和分拣轨迹建立最短路径模型，采用末端加速度建立机构稳定性优化模型，并通过改进粒子群优化算法对目标进行优化。结果表明，改进后的算法能有效地提高系统的效率，在输送速度100 mm/s时，抓取成功率由96.8%提高到100%，抓取效率由1.62个/s提高到1.98个/s，具有一定的实用价值。在现有的试验条件下，高速并联食品分拣机器人抓取控制策略的研究还处于试验阶段，后续将不断完善整个高速并联食品分拣机器人的功能。