洛必达法则在解析求极限类问题中的应用

王丽丽

(大同师范高等专科学校 数学系，山西 大同 037000)

1 洛必达法则的主要类型

洛必达法则是在一定条件下对分子和分母分别求导，然后求极限，进而获得不定式值的解题方法。根据现有认知水平，两个无穷大之比或两个无穷小之比的极限有存在的可能性，但也有不存在的可能性。因此，求解这类不定式极限时需要将其转化为重要极限形式或运用极限运算法则的表达形式展开计算，而洛必达法则是求解这类不定式极限的通用方法。

上述法则中，将a替换成∞，等式同样成立[3]。

上述法则中，将a替换成∞，等式同样成立。

1.3 其他类型不定式

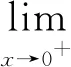
(2)1∞型不定式求极限时可以利用eln a=a的对数性质，将题目中的函数转换为以e为底数的指数型函数，再继续求极限，即1∞=eln1∞=e∞·ln1=e0·∞。此外，针对不同题目可以用不同方法替换题目中的函数，例如ln(1+x)～x，当x从正轴无限趋向于1时，x-1无限趋向于0，可运用等价无穷小替换公式将ln(1+x)替换为x，再继续求解。

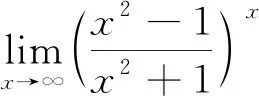
(3)∞0型、00型不定式求极限时同样可以利用eln a=a的对数性质，将题目中的函数转换为以e为底数的指数型函数，即∞0=eln ∞0=e0·ln∞=e0·∞，00=eln 00=e0·ln 0=e0·∞，再继续求极限。

2 洛必达法则应用注意事项

应用洛必达法则可以将不定式的极限运算转变为较简单的导数运算，为求解极限提供了一种较为简单、有效的运算途径，但应用洛必达法则解题时必须注意以下几点[5]。

2.1 洛必达法则应用条件

2.2 结合多种方法解题

上述过程首先利用指数相乘的基本运算方式进行简单变换，然后利用等价无穷小公式进行变换，减少了计算量，提升了正确率且易于理解。

2.3 洛必达法则条件弱化

3 洛必达法则的详细应用

洛必达法则是解决绝大多数求极限类问题的方法，但计算过程中一般会融合其他方法。以下从含根式函数极限、含三角函数极限、幂指数类函数极限三方面进行求解。

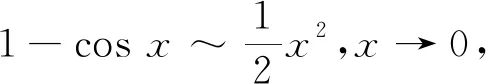
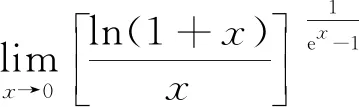
综上，在求解极限类问题的过程中，洛必达法则发挥着极其重要的作用。