基于TWFPN算法的配电网故障主动诊断研究

张婷婷，张信群，许 敏

(滁州职业技术学院 机械与汽车工程学院，安徽 滁州 239000)

随着分布式电源的应用，有源配电网逐渐取代传统配电网而被广泛应用。黄光球等[1]、王丽丽等[2]发现，采用传统矩阵计算进行有源配电网故障诊断时存在逻辑过于简单的问题，已不能满足断路器数量较多和具有相关保护的有源配电网故障诊断，亟须设计一种有源配电网故障诊断方法。本研究以闭环有源配电网故障主动诊断为对象，构建了有源配电网故障主动诊断模型。考虑到闭环有源配电网发生故障时通常采用速断、限时速断、过流保护进行阶段式保护，而各阶段保护具有鲜明的时序性和逻辑性[3]，本研究设计了一种时序连接加权模糊Petri网(TWFPN)故障诊断模型，通过引入时序连接和高斯分布函数防止了故障误判，并减少了信息丢失等的影响，为有源配电网故障诊断提供了一定的帮助。相较于典型的配电网故障诊断算法，该算法对闭环有源配电网单线故障和多线故障具有更高的诊断正确率。

1 基本算法

TWFPN是以加权模糊Petri网为基础，根据有源配电网时序连接规则建立的一种时序连接加权模糊Petri网[4]。为具体描述TWFPN，本研究以文献[5]设置的11元组TWFPN11进行说明。该元组模型如下：

STWFPN={P,T,N,I,O,W,U,B,fg,TC,Ttime}，

(1)

式中：P={p1，p2，…，pn}，表示TWFPN模型库所集合，n为库所数量；T={t1，t2，…，tm}，表示变迁集，m为变迁数量；N表示故障蔓延方向数量；I表示库所到变迁路径集合，为一个n×m矩阵，若该库所有通向变迁的路径，则矩阵对应元素值为1，反之则为0；O表示变迁到库所路径集合，为一个m×n的矩阵，若该变迁有通向库所的路径，则矩阵对应元素值为1，反之则为0；W=diag(W1，W2，…，Wn)，表示输入弧权值矩阵；U=(U1，U2，…，Um)，表示变迁置信度T向量，W和U结合，即事件发生对下一事件的影响；TC={C1，C2，…，Cm}，表示变迁阈值向量，若输入权值合并后小于阈值，则变迁失败，反之则变迁成功；B={B1，B2，B3}={RCBNs，CBN，…，RCBMX，CBM，…，RCBPg，CBP}，表示有效时序集合；fg=e-4.5(x-1)2表示高斯分布函数[6]；Ttime表示时序关系图。

2 基于TWFPN的配电网故障主动诊断模型构建

配电网的继电保护动作通常具有明显的时序性，所以可采用TWFPN对其进行故障诊断。根据配电网故障发生时断路器出口时序和各保护阶段情况，将诊断模型分为两部分：一是根据Ttime规则确定集合B；二是将集合B内元素作为初始库所数据进行矩阵计算，由此得到线路可能出现故障的概率。以闭环的配网线路为例，其TWFPN诊断模型如图1所示。

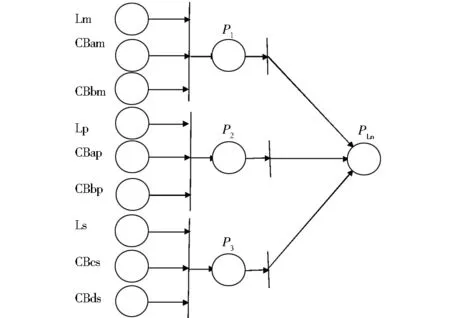
图1 配电网线路TWFPN主动诊断模型

图1中，库所Lm、Lp、Ls分别表示线路的主保护、近后备保护、远后备保护；CBam和CBbm为主保护断路器出口情况；CBap和CBbp为近后备保护断路器出口情况；CBcs和CBds为远后备保护断路器出口情况；PLn表示线路Ln发生故障的最终概率。库所Lm、Lp、Ls分别由B1、B2、B3集合处理后得到。以Lm为例，当B1中值为1的元素数量超过2的时候(开环则为1)，此时主保护动作可靠，将Lm置为1，反之则置为0。当Lm置为1时，若在断路器出口的同侧存在1个及以上的速断保护或限时速断保护，则将Lm对应的断路器值置为1，即CB3m为1，反之为0。DG侧采用相同方法设置。同理，对于由集合处理得到的Lp和Ls进行上述设置，即可实现对所有时序集合的处理，得到第一梯度的初始库所。

考虑到传统推理对库所和变迁值处理时会因为子站信息丢失或断路器拒动，造成故障诊断结果存在误差，导致最终误判，本研究结合保护与对应断路器出口时序性，引入高斯分布对构建的TWFPN模型初始库所、变迁阈值等进行了重新定义[7]。

线路中断路器和各阶段保护置信度设置见表1。

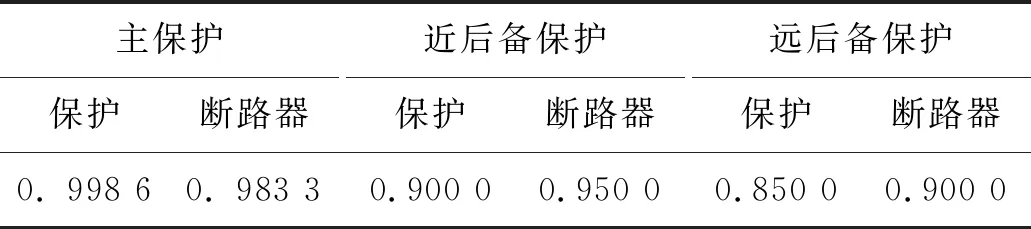
表1 置信度设置

置为0的初始库所置信度设置为0.2，变迁阈值设置为0.2，元件故障越限值设置为0.7，初始库所到第一次变迁的输入弧权值分别设置为0.5、0.25。在第一次变迁后，得到第2列库所输出弧权值，然后再进入下一步变迁的输入弧权值设置。

采用上述TWFPN模型对配电网故障进行主动诊断的流程见图2。

图2 基于TWFPN的配电网故障主动诊断流程

3 仿真实验

3.1 实验环境

CPU为 Intel core i5 9300H，内存为8 G。本实验在MATLAB 2018b软件中进行仿真。输入数据为配电网故障警报信号和SOE时序信息，输出数据为故障线路及异常继电保护信息。考虑到无法确定部分继电保护信息的状态，故在程序中通过“继电保护设备故障情况”“告警信息丢失”“畸变情况”进行反映。

3.2 算例验证

为验证TWFPN算法对配电网故障主动诊断的有效性，采用某区域的闭环有源配电网实际现场信号进行故障诊断测试。该配电网网络结构如图3所示。

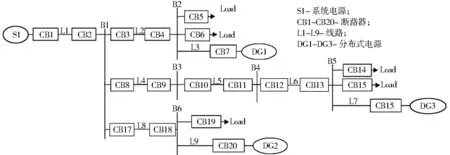
图3 闭环有源配电网网络结构

考虑到不同地区在时延设置方面存在差异，本研究选用实验配电网区域的时延设定：限时速断保护动作时延(ms)为[310，340]；速断保护动作时延(ms)为[10，40]；近后备和远后备过电流保护动作时延以系统结构为标准。具体时序整定值见表2，表中过电流保护所处位置1～20依次对应断路器CB1～CB20；断路器出口信息时延(ms)为[20，40]。

表2 过电流保护时序整定值

3.2.1单线路故障情况

为验证本算法的主动诊断效果，以实例1为例进行诊断。

实例1 L5发生故障且CB11拒动，CB13丢失出口信息，故障SOE信息为[CB10s(40 ms)，RCB10s(10 ms)，RCB11s(15 ms)，RCB11x(330 ms)，RCB11g(1 100 ms)，RCB13g(1 350 ms)]。其中，s、x、g分别对应断路器的速断信号、限时速断信号、过流保护信号，时间表示各信号相对于故障发生时的时延，一般为最早速断保护出口的时间往前推10 ms[8]。

首先，根据时序连接图，计算CB10s(40 ms)隶属度μR=0.804。由于后时序没有连接，所以结束推理。然后，选取SOE剩余信息中最初时序信息RCB11s(15 ms)，按照同样方法得到RCB11x(330 ms)的隶属度μR=0.805。以此类推，可得到RCB11g(1 100 ms)的隶属度μR=0.805，RCB13g(1 350 ms)的隶属度μR=0.908。由上述隶属度结果可知，所有信息的隶属度均大于0.5[9]，说明以上信息均为L5的有效出口信息。最终，得到集合B1=[1 1 1 0 0 0 1 0 0 0 0 0]；B2=[0 0 1 0 0 0 1 0]；B3=[0 0 1 0]。根据TWFPN模型构建的初始库所集合设置可知，本实验的初始库所集合P=[1 1 0 1 0 0 1 0 0]。

①计算输入弧权值：

Winput=W·I，

(2)

式中：W和I分别为n×n和n×m的矩阵，表示库所到下一步变迁的置信度和库所到变迁的映射。

通过计算可得到

②计算第一梯度变迁，合成输入可信度：

(3)

式中：α0是1×n的矩阵，表示变迁次数为0的库所矩阵。本实例中，α0=[0.998 6 0.983 3 0.2 0.9 0.2 0.2 0.85 0.2 0.2 0 0 0 0]，可得

(4)

③比较该处变迁与变迁越限阈值，得到该处真正变迁值

(5)

④计算第一梯度库所值

(6)

由上述计算结果可知，梯度1、2的各库所值分别为[0.827 8 0.243 9 0.165 3]和[0.776 7]。因此，得到故障率为0.776 7，大于阈值0.7[10]，得出L5线路发生故障。

反向搜索L5线路。由于该线路已被诊断为发生故障，故第二梯度库所P2>0.7，不存在问题。接下来，考察第一梯度库所值P1，由于P1[1]>0.2、P1[2]>0.2、P1[3]<0.2，说明近后备产生保护动作，且保护断路器拒动。

最后考察B3，发现远后备保护信息完善，但不存在其对应的断路器出口信息，由此可判断故障的具体情况为CB11拒动、CB13出口信息丢失。

综上可得，本算法对该配电网故障的诊断结果如下：L5线路故障，CB11断路器拒动、CB13断路器出口信息丢失。该结果与实际故障情况一致，说明本算法有效可行。

3.2.2多线路故障情况

多线路故障情况以实例2为例进行诊断。

实例2L2、L5两条线路发生故障，且CB10拒动并丢失过流保护信息，CB11丢失出口信息。SOE故障信息为[RCB10s(20 ms)，RCB3s(25 ms)，CB3s(55 ms)，RCB4s(10 ms)，CB4s(35 ms)，RCB10x(320 ms)，RCB8g(1 200 ms)，CB8(1 230 ms)，RCB11s(30 ms)]。

采用与单线路故障情况相同的方法，从最初时序信息开始推理计算得到CB4s(35 ms)的隶属度μR=0.846，RCB10x(320 ms)的隶属度μR=1.000，RCB8g(1 200 ms)的隶属度μR=0.702，CB8(1 230 ms)的隶属度μR=0.708，CB3s(55 ms)的隶属度μR=0.902。由于RCB11s(30 ms)为初始时序且在速断保护时序范围内，故其隶属度μR=1。由以上看出，所有信息的隶属度均大于0.5，说明信息均为有效出口信息。

首先对L2进行分析，可得到集合B1=[1 1 1 1 0 0 0 0 0 0 0 0]，B2=[0 0 0 0 0 0 0 0]，B3=[0 0 0 0]，则其初始库所集合P=[1 1 1 0 0 0 0 0 0]，梯度1和梯度2的库所值分别为[0.999 6 0.041 8 0.359]和[0.955 7]，可得到该元件发生故障的可能性为0.955 7，大于0.7，即可判定L2线路发生故障。同理，可判定L5线路发生故障。

然后对L2线路进行反向搜索，由于L2发生故障，其第二梯度库所值大于0.7，不存在问题。接下来，考察其第一梯度库所值。由于P1[1]>0.2，可判定该线路主保护和其对应的断路器可正确动作。最后考察其元素集合B1、B2、B3，可发现B1中RCB10s、CB10s、RCB11s、CB11s均为1，B2、B3为空集，则可判定该吸纳路继电保护设备正常，通信系统没有发生故障。同理对L5线路进行反向搜索，可判定CB10拒动且其过流保护信息丢失，同时CB11出口信息丢失。

综上，本算法对该配电网多线路故障的诊断结果如下：L2、L5线路故障，CB10拒动且其过流保护信息丢失，同时CB11出口信息丢失。该结果与实际故障情况一致，说明本算法有效可行。

3.3 算法比较

为验证本算法的优越性，本研究在上述2个实例的基础上增加了11个故障实例，共计13个故障实例，分别采用本算法、文献[11]算法、文献[12]算法对13个故障实例进行诊断，结果如图4和图5所示。由图4可知，本算法的诊断速度较慢，原因是本算法在信息预处理过程中添加了SOE时域信息，增加了计算量。但整体来看，本算法与对比算法的计算速度处在同一等级。由图5可知，本算法对故障的诊断正确率最高，可达到95%，两种对比算法的故障诊断正确率均在80%以下。总体来说，本算法相较于典型的配电网故障诊断算法具有一定的优越性，可用于实际配电网故障诊断。

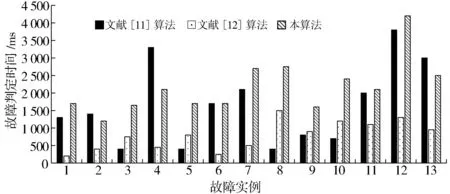
图4 不同算法故障诊断速度对比

图5 不同算法故障诊断准确率对比

4 结语

本研究构建了基于TWFPN算法的配电网故障主动诊断模型，引入时序连接和高斯分布函数，降低了配电网故障线路误判概率，可对速断信号、限时速断信号、过流保护信号进行准确诊断，同时避免了配电网信息丢失或拒动，可有效诊断有源配电网的单线路故障和多线路故障，诊断结果与实际情况相符。相较于典型的配电网故障诊断算法，本研究提出的算法在故障诊断速度和诊断正确率上具有一定的优越性。