基于粒子群优化算法的充填体单轴抗压强度预测研究
2022-04-07黄晓红崔贺佳刘志义刘利平张凯月
黄晓红,崔贺佳,刘志义,刘利平,张凯月
(1.华北理工大学 信息工程学院,河北 唐山 063210;2.华北理工大学 矿业工程学院,河北 唐山 063210;3.河北省矿业开发与安全技术重点实验室(华北理工大学),河北 唐山 063210)
0 引 言
随着国家科学技术进步和经济增长,环境问题备受关注,其中矿山开采非常突出。全尾砂充填已被广泛用于预防和减轻矿山开采过程中的安全和环境问题,其充填体强度是衡量充填质量的重要指标。国内外众多学者研究了影响充填体强度的多种因素,如水泥含量、尾矿类型和固化时间等[1-5],但充填体强度试验复杂、工作量大、耗时长、成本高,因此,寻找一种简单可靠的方法预测充填体强度势在必行。
近几年,随着人工智能快速发展,各类算法成熟,为研究矿山充填体复杂的非线性关系提供了新方法。外文文献预测充填体强度方法较为先进,如QI C C等[6]提出加速回归树(BRT)算法,用于输入和输出间的非线性关系预测充填体强度建模,将粒子群优化算法(PSO)用于BRT超参数调整预测充填体抗压强度,并采用遗传编程[7]和遗传规划(GP)对充填体抗压强度进行准确预测;QI C C等[8]还研究了纤维对混凝土性能的影响,并评估所有混凝土混合物的性能和超声脉冲速度,然后使用前馈人工神经网络和PSO生成多项式模型,预测混凝土力学性能。
国内对于充填体强度预测也进行了诸多研究,如李立涛等[9]基于正交试验建立了BP神经网络模型,预测充填体强度并研究其影响规律;刘恒亮等[10]采用灰色关联度理论提高样本可信度,基于正交试验建立BP神经网络模型,准确预测充填体强度;史秀志等[11]借助PCA结合BP神经网络预测充填体强度;魏微等[12]通过改进的BP神经网络模型预测充填体强度。
以上研究大多使用BP神经网络进行强度预测,但BP神经网络容易陷入局部最小过拟合,导致精度减小,预测不精确。支持向量回归(support vector regression,SVR)是一种基于统计学习理论的机器学习方法,由于其出色的学习性能,被广泛应用于解决分类与回归问题。因此,本文根据试验数据建立PSO-SVR模型,即利用PSO对SVR精度和参数进行全局优化,以期实现充填体强度的高精度预测。
1 试 验
1.1 试样制备
试验条件:采用正交试验,每组方案制作3个试样,为避免偶然性,共制备216个充填体试样。本次试验材料主要有某金矿的尾砂和水泥。常温制浆,制浆水为自来水,将尾砂和水泥混合物完全混合并倒入塑料模具(直径50 mm,高100 mm)。脱模后的充填体在约25 ℃和90%湿度的养护箱中固化,到规定龄期后测试其单轴抗压强度。试验主要参数如下。
(1)模拟输送质量分数:60%,65%,70%,75%。
(2)灰砂质量比:1∶4,1∶6,1∶8,1∶10,1∶12,1∶16。
(3)养护龄期:7 d,14 d,28 d。
1.2 单轴压缩试验及结果分析
利用Instron 250 kN刚性液压伺服材料实验机,对所有样本以0.5 mm/s匀速加载测定单轴抗压强度,结果如图1所示。每3个柱为一组,代表一种灰砂比。从整体看,质量分数为75%,灰砂比为1∶4,养护时间为28 d时其单轴抗压强度最大,随着质量分数增大,充填体单轴抗压强度明显增大。

图1 充填体单轴抗压强度试验结果Fig.1 UCS test results
质量分数60%的放大图显示:
(1)养护28 d时抗压强度最大。
(2)养护时间28 d时,随着灰砂比减小,充填体抗压强度随之变小。
试验结果表明,充填体单轴抗压强度的主要影响因素为养护龄期、质量分数和灰砂比。从微观分析,主要原因是发生了水化反应[16]。充填体试样在不同条件下主要发生4种反应,分别生成水化硅酸钙凝胶相,氢氧化钙相,水化硫酸铝钙相和未水化水泥熟料颗粒相。尾砂胶结充填体的单轴抗压强度主要取决于硬化水泥浆、界面过度区和骨料组合的综合效应,其中硬化水泥浆和界面过渡区的强度均与水泥强度有关。按照复合材料力学方法,尾砂胶结充填体可看作是由尾砂骨料和水泥凝胶(固相)、毛细水(液相)和空气(气相)三相组成,如图2所示。分析尾砂和水泥的粒径内部结构,主要含有尾砂、水泥凝胶、各种孔隙和气泡裂纹等,在水泥浆体与尾砂凝结过程中,主要靠水化硅酸钙凝胶相薄片将尾砂颗粒连接在一起,水泥浆基体和界面过渡区的强度决定了尾砂胶结充填体的单轴抗压强度。
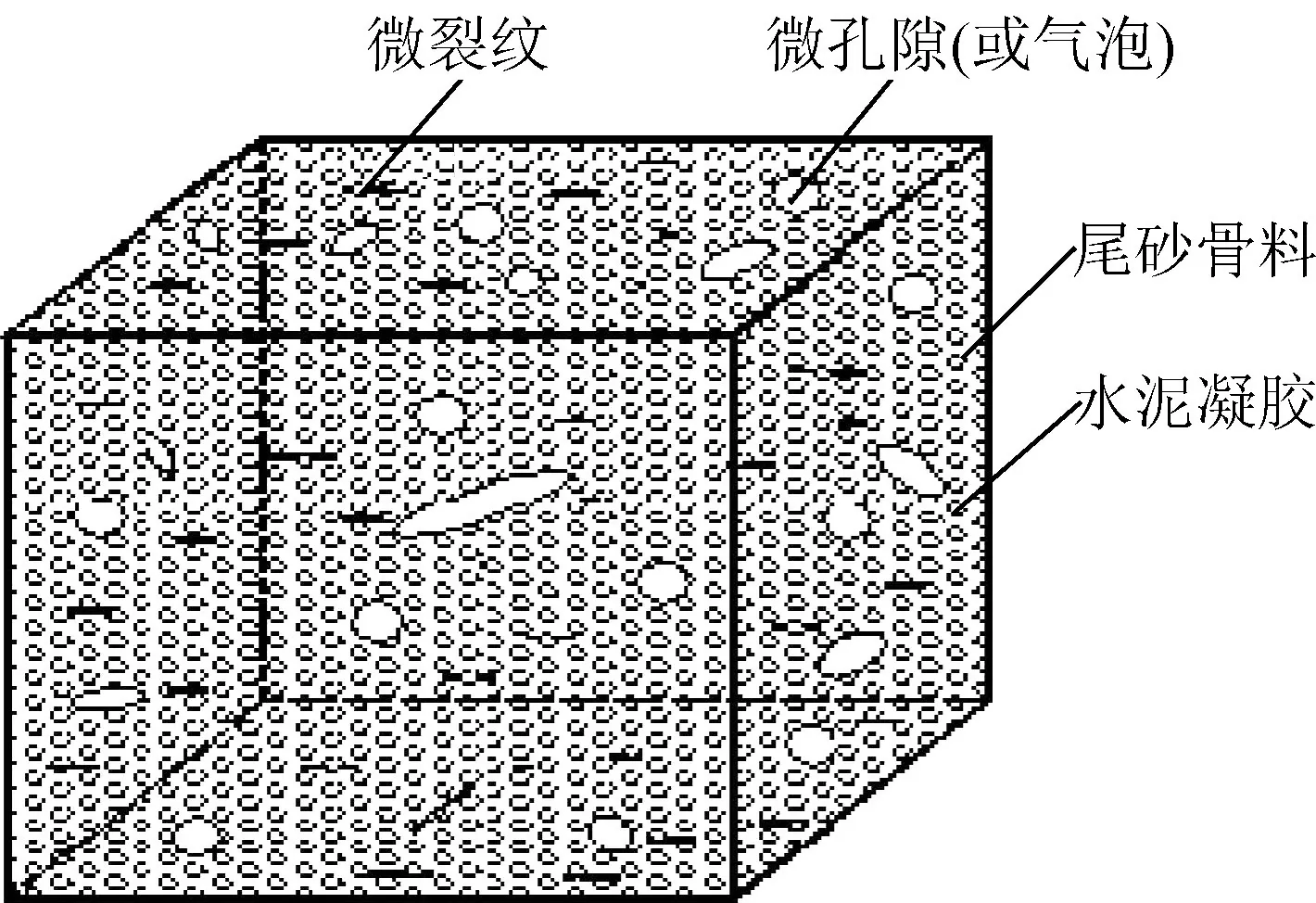
图2 尾砂胶结充填体细观结构示意Fig.2 CPB schematic diagram of the structure
对不同强度的充填体进行电镜扫描,显微电镜图如图3~4所示。在扫描电镜下,硬化水泥浆体有4个主要固相:水化硅酸钙凝胶相(缩写为C—S—H凝胶),氢氧化钙相(缩写成CH晶体),水化硫酸铝钙相和未水化水泥熟料颗粒相。图3中尾砂胶结充填体养护龄期为56 d,单轴抗压强度为1.6 MPa,灰砂比较大,养护时间长,反应时间久,C—S—H薄片将尾砂颗粒连接在一起。由图3可以看出,水泥水化产物多,充填体内部孔隙少,最终宏观表现为单轴抗压强度大。图4为低强度尾砂充填体电镜扫描图,养护龄期56 d,单轴抗压强度0.05 MPa,其内部孔隙多,水化反应产物少。

图3 强度较高的尾砂充填体SEM显微电镜图Fig.3 SEM microscopic electron micrograph of the tailings cemented backfill with higher strength

图4 低强度尾砂充填体SEM显微电镜图Fig.4 SEM microscopic-electron micrograph of the tailings cemented backfill with lower strength
综上分析,一定程度上灰砂比越大、质量分数越大、养护时间越长、反应时间越久,其硬化水泥浆体百分比越大,最终导致产物增多,充填体内的孔隙减少,宏观表现为充填体单轴抗压强度增大;相反,充填体内产物减少、孔隙增多、宏观表现为充填体单轴抗压强度减小。因此,充填体单轴抗压强度主要影响因素为养护龄期、充填体质量分数和灰砂比。
充填体试样的单轴抗压强度随养护龄期、灰砂比、质量分数增加而增加,本文通过物理和化学分析,将这3种因素作为主要输入因子,用于预测充填体强度。
2 充填体强度预测
2.1 支持向量机回归模型(SVR)
支持向量机(support vector machine,SVM)以统计学理论为基础,与传统方法不同,SVR是SVM用于预测回归的模型,可解决小样本、非线性、高维度问题,能够应用到机器学习回归分析等领域。SVR以统计学理论为基础,以结构风险化、最小化为原则,相对于BP神经网络,SVR保证了机器学习具有良好的泛化能力。SVR非常适合处理多维非线性回归,首先使用非线性映射函数φ从低维特征空间映射到高维特征空间,其次在高维特征空间进行线性回归运算。
2.2 PSO优化SVR超参数
本文采用PSO算法,PSO起源于大自然中鸟群捕食行为,其基本思想:通过种群中个体之间的相互协作和信息共享寻找最优解,粒子群中的每个粒子相当于鸟群中的一只鸟并且都赋予记忆功能,所有粒子在一个D维空间进行搜索,而且每个粒子仅有两个属性,即速度和位置,速度代表移动快慢,位置代表移动方向。每个粒子单独行动寻找最优解,然后将自己的最优解与其他粒子共享,所有粒子相互比较,找到整个粒子群的最优解并作为当前的全局最优解。找到当前的最优解后,所有粒子根据自身状态调整自己的速度和位置,反复进行,最终寻找到最优解。利用充填体试验数据对网络进行训练,网络参数群体大小和最大迭代次数根据建议选择300和600,w,c1和c2建议为2,1.8和1.8。
2.3 充填体单轴抗压强度预测与结果分析
采用SVR与BP神经网络分别对充填体单轴抗压强度进行预测,图5和图6分别为SVR预测集和BP神经网络的充填体单轴抗压强度预测值与真实值对比。输入因子为固体含量(4类)、尾砂比(6类)、养护龄期(3类),输出因子为养护7 d,14 d,28 d的充填体单轴抗压强度试验值。

图5 SVR测试集预测结果与真实值对比Fig.5 Comparisons of SVR test set prediction results and real values

图6 BP神经网络预测结果与真实值对比Fig.6 Comparisons of BP neural network prediction results and real values
MSE是参数估计值与参数真值之差平方的期望值,MSE越小越好。在统计学中对变量进行线性回归分析,采用最小二乘法进行参数估计时,回归平方和与总离差平方和的比值R2越大越好,模型越精确,回归效果越显著。R2为0~1,越接近1,回归拟合效果越好。
由图5~6可以看出,SVR预测结果MSE小于BP神经网络预测的,并且R2提升幅度较大,说明可以用于预测充填体单轴抗压强度,且验证了SVR回归泛化能力大于BP神经网络的[12]。
基于粒子群优化算法SVR网络模型预测充填体单轴抗压强度中的训练集和测试集预测值与真实值对比如图7~8所示,PSO-SVR测试集的MSE=0.000 726 13,R2=99.304%,表明该模型可以准确用于预测充填体强度。图9为基于粒子群优化算法的BP神经网络模型的预测值与真实值对比,MSE=0.000 778 43,R2=93.192%,表明粒子群优化算法可以用于BP和SVR的参数优化。对比图6~7发现,PSO-SVR更适合用于充填体单轴抗压强度预测,其准确率相对于PSO-BP有大幅度提升。

图7 PSO-SVR训练集预测结果与真实值对比Fig.7 Comparisons of PSO-SVR training set prediction results and real values
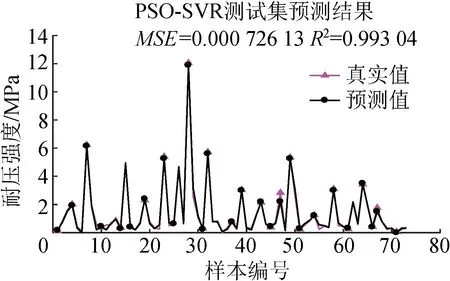
图8 PSO-SVR测试集预测结果与真实值对比Fig.8 Comparisons of PSO-SVR test set prediction results and real values

图9 PSO-BP神经网络测试集预测结果与真实值对比Fig.9 Comparisons of PSO-bp test set prediction results and real values
表1为3种模型的MSE和R2的比较。由表1可知,PSO-SVR的R2比SVM的和PSO-BP模型的分别高出5.22%和6.11%,MSE在粒子群优化后相对于SVM模型的下降了20.86%。PSO-BP与BP模型相比,其MSE减小45.39%,R2增长3.42%。

表1 预测模型比较结果Tab.1 Comparison of results prediction models
由表1分析可知,PSO-SVR模型成功学习了它们之间的关系——输入和输出,线性拟合程度最高,这意味着可以有效避免不合适和过度拟合。
本文主要验证了PSO-SVR预测充填体单轴抗压强度方法的适用性。与传统单轴抗压试验相比,优点如下:
(1)PSO-SVR方法成本低、耗时少和非破坏。粒子群优化算法适用于SVR和BP神经网络模型参数的优化问题。
(2)一般模型可以使用更全面的数据轻松构建和更新,PSO-SVR的泛化能力比使用经验方程更好。
(3)PSO-SVR在本文中预测的相关系数可达99.3%,其精度可用于预测充填体单轴抗压强度。
本文方法遗漏了其他影响充填体单轴抗压强度的变量,如外加剂类型、硫含量、温度和湿度等,这是当前研究局限性所在,还需进一步研究其他影响变量,如尾矿类型、更长的养护时间等。
3 结 论
(1)PSO优化算法比BP神经网络线性拟合度提高了3.42%,比SVM线性拟合拟合度提高了5.22%,表明PSO优化算法是有效的,可以提高矿山充填体单轴抗压强度的预测精度。
(2)与PSO-BP模型相比,PSO-SVR模型线性拟合度提高了6.11%,均方误差更小,表明PSO-SVR更适合充填体单轴抗压强度预测。
(3)PSO-SVR模型适用于矿山充填体强度的预测,由216个样本构造的模型看,PSO-SVR模型线性拟合度为99.304%,说明该模型可用于充填体的单轴抗压强度预测,且预测精度高。
