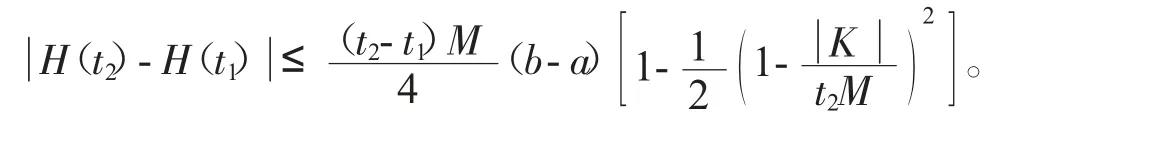Lipschitz 函数Hermite-Hadamard 型不等式的加强

时统业，曾志红

（1.海军指挥学院，江苏 南京 211800；2.广东第二师范学院 学报编辑部，广东 广州 510303）

1 引理

Hermite-Hadamard 不等式是指

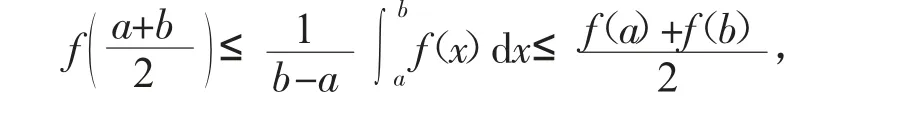
其中，f 是［a，b］上的凸函数。

关于Hermite-Hadamard 不等式的改进、推广和加细已有很多结果，可见文献［1-23］。文献［4］引入了定义在［0，1］上的函数，证明了当f 是［a，b］上的凸函数时，H（t）是［0，1］上单调增加的凸函数，从而利用H（t）加细了Hermite-Hadamard 不等式的左边部分。

定义1 设f：［a，b］→R，如果存在常数M，使得对于任意x1，x2∈［a，b］，有，则称f 是［a，b］上的M-Lipschitz 函数。

文献［6］证明了当f 是［a，b］上的M-Lipschitz 函数时，H（t）是-Lipschitz 函数，即对任意t1，t2∈［0，1］，有

特别地，有

本文将建立Lipschitz 函数的一些不等式，给出不等式（1）～（3）的加强。在证明双边不等式时，因为当f 是定义在［a，b］上的M-Lipschitz 函数时，（-f）也是定义在［a，b］上的M-Lipschitz 函数，在证明了右边不等式之后对（-f）应用已证结果，则左边不等式也得证，所以我们只证明右边不等式。

2 主要结果

定理1 设f 是［a，b］上的M-Lipschitz 函数，0＜t1＜t2≤1，则有

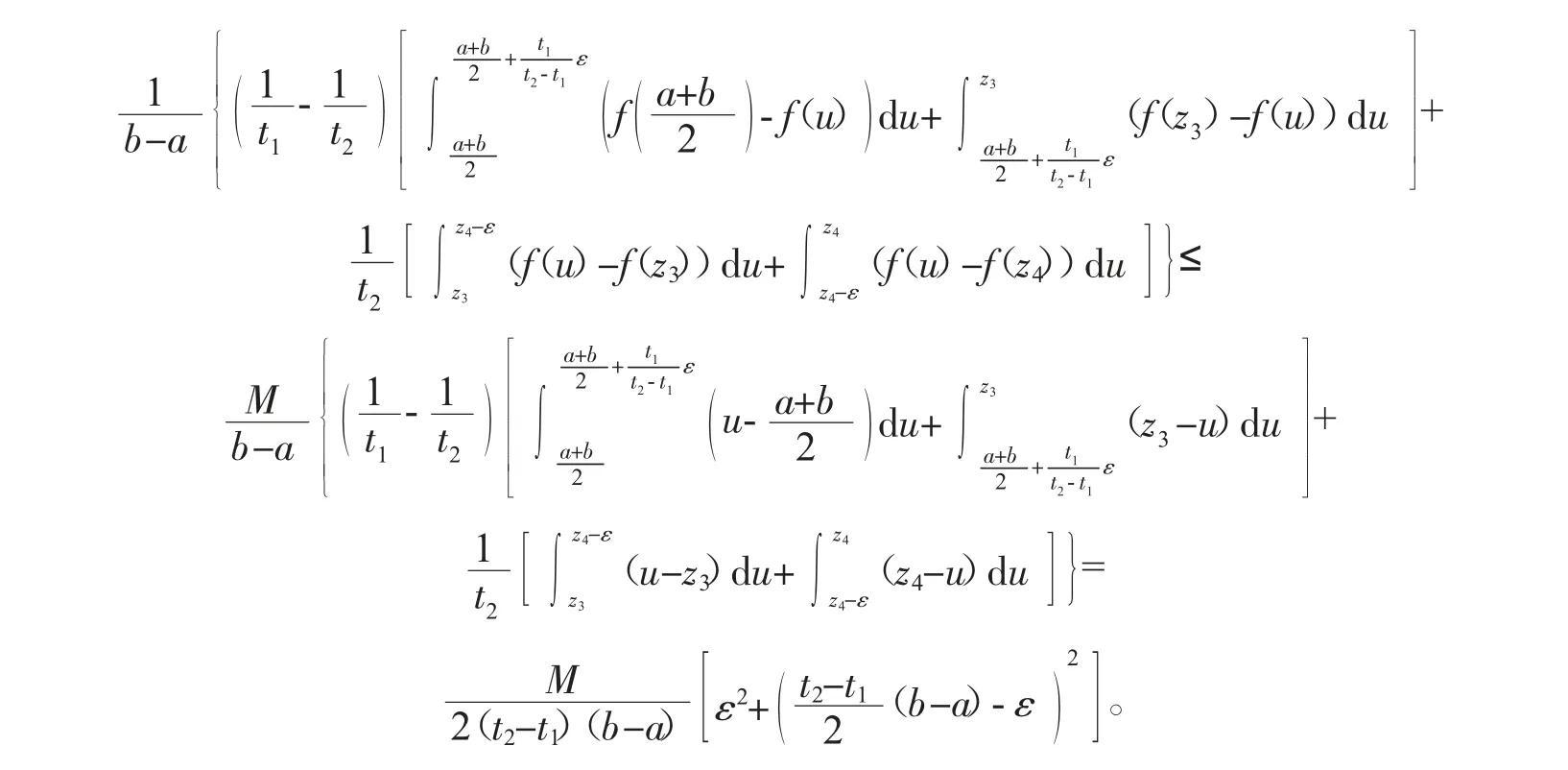
接下来类似于式（6）的证明得到

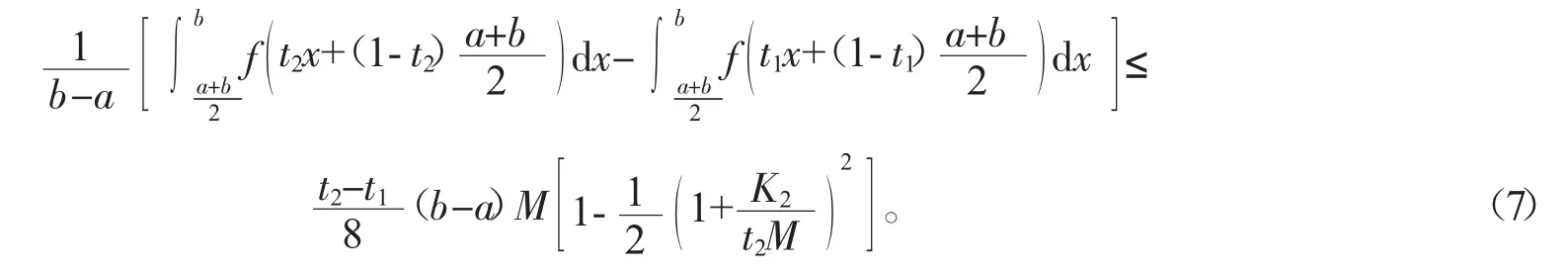
将式（6）与式（7）相加，则式（4）从右边数起的第2 个不等式得证。利用函数x2的凸性，式（4）从右边数起的第1 个不等式得证。

推论1 设f 是定义在［a，b］上的M-Lipschitz 函数，0＜t1＜t2≤1，则有

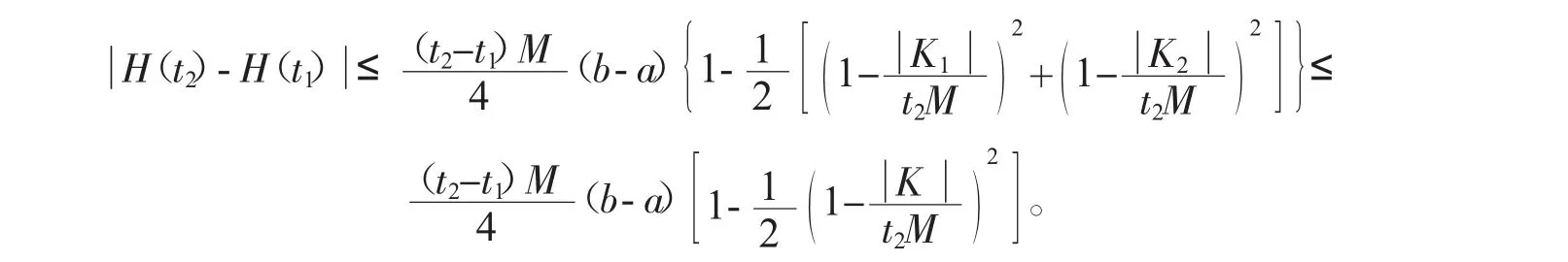
定理2 设f 是定义在［a，b］上的M-Lipschitz 函数，则对任意t∈（0，1］，有

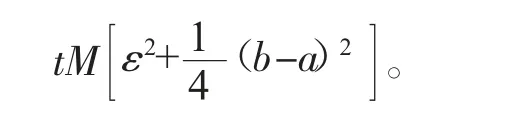
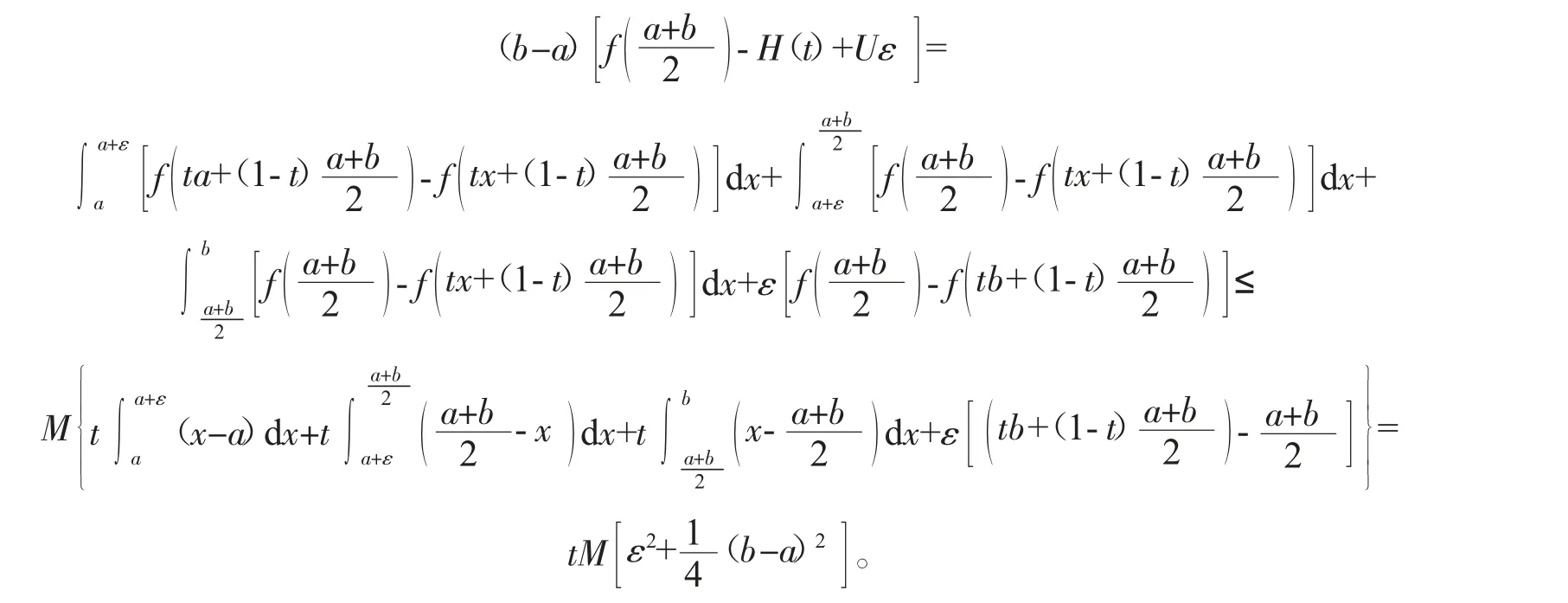
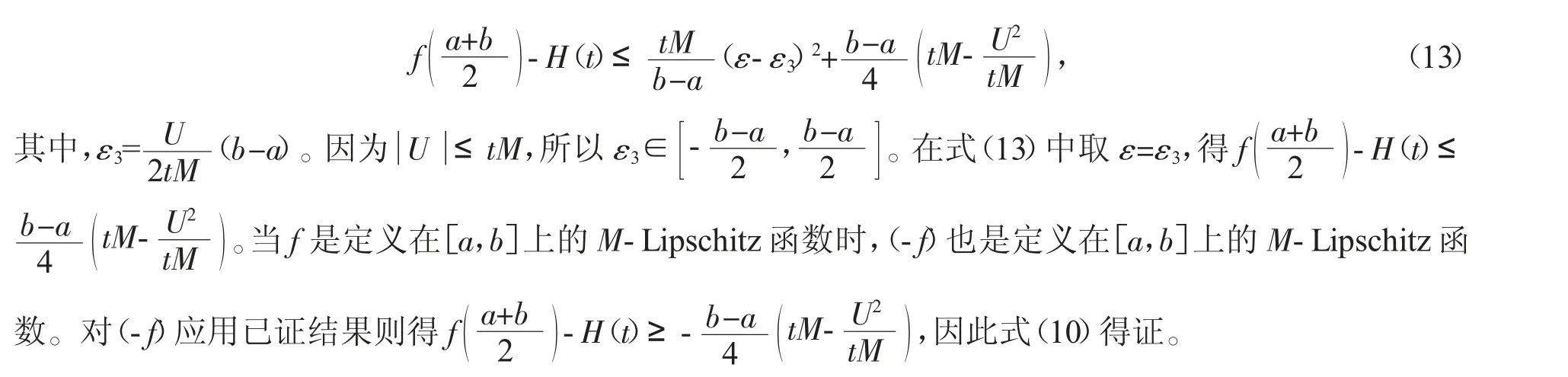
推论2 设f 是定义在［a，b］上的M-Lipschitz 函数，则对任意t∈（0，1］，有

注1 综合定理1 中的式（4）和定理2 中的式（9），对任意t1，t2∈［0，1］，t1＜t2，都有

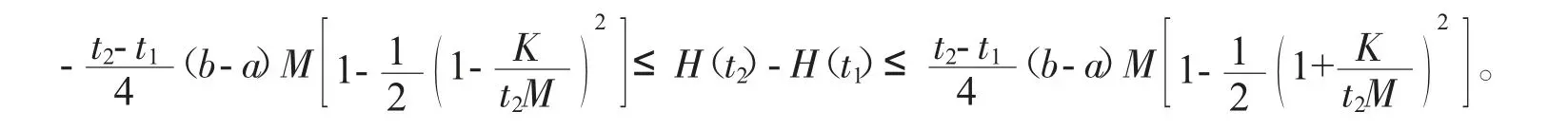
注2 综合推论1 和推论2，对任意t1，t2∈［0，1］，t1＜t2，都有