基于PROSAIL模型的高寒冬季枯草关键参数阈值率定

梁 好，徐维新*，段旭辉，张 娟，代 娜，肖强智，王淇玉

1. 成都信息工程大学资源环境学院，四川 成都 610225 2. 青海省气象科学研究所，青海 西宁 810001

引 言

青藏高原独特的生态环境与自然气候条件是推动全球变化研究与认识深化的重点区域。 其中，高寒草地是青藏高原最主要的植被覆盖类型以及我国大规模生态环境保护与建设的对象。 冬季是草原过度采食与生态破坏的主要时期，冬季牧草即枯草的存量则是保护生态平衡与畜牧业生产与灾害防御的关键参量。 已有工作表明，枯草是生物量、水分、叶绿素等参数持续协同变化的结果，对其关键参数的认识具有重要的科学意义与直接的应用需求。 然而，当前国内外对冬季枯草的研究报道极少，而青藏高原地区冬季枯草监测空白的现状，则与枯草性状参数认识的不足有直接关系。

传统草地监测主要依靠人工采样完成，不仅费时费力，更难以完成大面积的监测。 近年来，辐射传输模型PROSAIL由于可以定量描述色素含量、水分、叶面积指数等性状参数对反射光谱的影响，而被广泛用于植被反演监测和机理研究中[1]。 多项研究指出PROSAIL模型在现实环境、模型复杂性、准确性和计算时间之间达成了良好的统一[2-3]，使其适用于多视角高光谱数据的分析和反演。 Berger等[4]对1992年到2017年间281篇与PROSAIL相关的论文分析发现，利用PROSAIL模型针对多种农作物(以小麦、玉米、甜菜为主)、森林及天然植被(草地，灌木)展开的研究，均取得了成功应用的同时，获得并提升了对各类植被反射光谱特征与植被性状参数作用的认识。 梁顺林等[5]指出准确的参数运行区间是基于PROSAIL模型开展相关研究与反演活动的基础。 然而，目前针对衰落期植被参数及其光谱特征的研究鲜有报道，个别研究仅作为生长期对照组而涉及衰落期[6-7]，缺乏对衰落过程中的各参数变化与机理状态的系统研究。

研究将利用PROSAIL模型，结合实测光谱与性状参数，通过模拟枯草冠层反射率曲线，探究PROSAIL模型对枯草的适用性，完成模型敏感性与不确定性分析。 在此基础上率定高寒枯草各项性状参数及其取值范围，最终得到LAI，LAD和Cm等关键参数取值区间参考表。 为利用模型对枯草进行研究和反演提供有利的基础数据支撑，并期望推动对枯草性状参数的认识与理解，为冬季枯草的遥感监测提供基础与方法支持。

1 实验部分

1.1 样本

样本采集于青海省海北藏族自治州西海镇中国气象局海北牧业气象试验站。 该试验场位于100°51′33″E，36°57′33″N，海拔3 140 m，地处青藏高原北部青海湖畔，属典型高寒天然草原。

在该试验场沿南北方向平行设置5行23个50 cm×50 cm枯草观测固定样方。 在牧草自然衰落并呈完全枯干状态的2020年11月27日进行观测采样。 采样时晴朗无风，枯草反射光谱及性状参数采样时间限定于9:30—15:30。 最终获得反射光谱230条，参数数据207条。

1.2 数据采集

1.2.1 光谱数据

使用ASD公司的FieldSpec4便携式地物光谱仪进行枯草反射光谱采集。 波长范围为350～2 500 nm，在可见光(VIS)和近红外(NIR)波段采样间隔为3 nm，短波红外(SWIR)采样间隔为8 nm，单次采集时间为0.2 s，探头视场角θ为25°。 按操作规范预热仪器并进行暗电流测试和参考板校正，为保证视场范围半径处于样方区内，观测时将探头高度保持在距地面约80 cm[8]进行观测。 每个样方每次同步采集10条冠层反射光谱，以保证观测数据可靠性与稳定性。

1.2.2 枯草性状参数

使用KonicaMinolta公司的SPAD502叶绿素仪进行枯草叶绿素含量同步观测。 该仪器测量窗口2 mm×3 mm，精度±1.0 SPAD, 采样间隔2 s，重现性±0.5 SPAD内。 测量时每个样方随机选择3株枯草，在枯草的上中下三部分各进行一次测量，取平均值作为该株枯草的叶绿素相对含量SPAD值。

使用直尺测量冠层高度L、平均叶片长度D，并使用量角器量取叶倾角。 随后用剪刀齐根剪下样方中所有牧草并装袋送回实验室。 同步记录观测时间、天气等状况。 根据式(1)计算得到热点参数Hspot。

(1)

使用天平(可读性0.01 g)测量枯草鲜重。 随后将同一样方的叶片均匀、分散平铺于多张A3纸上，经拍照及后期图像识别，获取样方叶面积指数(LAI)。 随后放入烘箱以70 ℃恒温烘干，烘至重量不再改变时作为该样方干重。 鲜重与干重相减得到枯草水分含量。

1.3 光谱模拟

1.3.1 PROSAIL模型

PROSPECT叶片光学传输模型与SAIL冠层双向反射率模型耦合组成PROSAIL模型。 Féret等[9]指出，最新推出的PROSPECT-D优于之前的版本，不仅降低了模型预测的不确定性、更好地恢复光合色素，同时能在可见光范围内以最小的误差模拟真实的叶片光学特性。 4SAIL模型引入了热点效应和土壤的二向反射特征, 提高了模型的数值稳定性和鲁棒性。 因此, 本研究采用PROSPECT-D与4SAIL耦合的PROSAIL模型进行枯草光谱模拟。

根据实测枯草性状数据，同时参考LOPEX93数据库与已有关于人工落叶林和冬小麦衰落期的研究成果[6-7]预设了模型运行初值(表1)。

1.3.2 模型敏感性分析

敏感性分析是定量或定性分析模型参数对模型结果产生的影响程度，对模型输入参数进行敏感性分析是进行参数率定的前提。 本研究采用全局敏感性分析方法EFAST法来完成PROSAIL输入参数敏感性分析。 EFAST法可以通过方差分解得到各参数的方差贡献比重，并以敏感性指数值来衡量各参数的敏感性。 其优点在于所得敏感性指数充分考虑了参数间耦合作用[10]。 其计算式为

(2)

式(2)中，V(Y)为全部参数的总方差，k为参数个数，Vi为第i个参数自身的方差，Vij为第i和j参数耦合作用的方差，V1…k为所有参数耦合作用的方差。

1.3.3 模型不确定性分析

不确定性是模型运行中参数间存在耦合作用无法完成全局最优判断导致的输出结果离散[11]。 不确定性分析可以识别模型不确定性的来源并量化参数对输出不确定性的贡献。 进行不确定性分析有助于提高枯草各参数组分间相互作用的认识和枯草衰落机理的理解。

采用全局敏感性指数与局部敏感性指数的差值来量化不确定性[12]。 如果某个参数与其他参数间存在耦合作用，造成了模型不确定性，那么它的全局敏感性指数值会大于局部敏感性指数值。 由式(2)知，两者的差值可写作Vij+V1…k，即为耦合关系指数，作为量化参数不确定性的指标。

1.3.4 枯草高敏感性参数率定

枯草反射光谱受不同草品种、倒伏状态、枯黄程度等影响，在光谱波形相似的情况下反射率绝对值波动较大，因此选取注重维度差异而不是数值差异的率定函数是必要的。

余弦距离[13]又称余弦相似度，衡量维度间取值方向的一致性，同时修正了变量间可能存在的度量标准不统一问题。 其不同于以距离为测度的欧式距离，也不同于以单位变化相似程度为依据的相关系数，在具有时序特性并对趋势(方向)敏感的曲线相似度评价中更有优势。 本研究采用余弦距离为参数率定评价函数。 通过对比不同输入参数取值下的模型模拟反射光谱与实测反射光谱间的余弦距离完成关键参数的率定。

2 结果与讨论

2.1 枯草光谱模拟结果

2.1.1 光谱数据预处理

对野外实测的固定样方光谱数据，逐一检查每个样方同步观测得到的10条光谱，剔除因仪器、吹风等因素引起的明显异常波动数据后，得到枯草原始光谱数据序列，每个样方随机挑选1条原始光谱展示于图1中。 由于PROSAIL模型模拟的有效范围为400～2 500 nm，本研究处理与分析均基于此区间完成。

从图1可以看出，枯草光谱在400 nm附近差异较小，随着波长的增大，枯草光谱间的反射率差异逐渐变大，并在1 300 nm附近达到反射率峰值(0.25～0.46)。 从1 300 nm开始，光谱反射率差异始终保持在0.1～0.25间，各样方曲线分布区间分散，区分度明显。

图1 2020年11月27日海北试验场实测枯草原始反射光谱Fig.1 Measured withered grass spectrum (MW) on November 27, 2020 in Haibei

为了更好凸显枯草光谱特征，消除不同光栅间的系统性“跳跃”偏差及个别光纤波动导致的“毛刺”性异常值。 利用ASD光谱仪附配的ViewSpecPro软件进行光谱预处理。 完成抛物线修正及同次观测样本的均值合成输出，实现数据校正的同时降低测量随机误差。

2.1.2 模型运行

根据1.3.1设定的模型模拟参数初始值，设定了较宽的模型运行参数阈值范围(表1)，以保证模拟结果处于可能的波动范围区间。

其中LAI，LAD，Cw，Cm，Cab和Hspot根据实测数据确定。 例如：Cm实测值在0.003～0.020之间，平均值为0.010，因此设定Cm参数运行范围为0.002～0.050。Cbr，Car，Cant，N初值参考文献[6-7]设定，OZA，SZA和RAA由试验点坐标和时间确定。

利用MATLAB对PROSAIL模型编程运行。 根据表1参数范围，以蒙特卡洛采样[14]方式获得在参数范围内随机分布的15 000组参数组合对，模型运行输出得到对应的15 000组模拟反射光谱。

表1 模型运行初值及范围设定Table 1 Initial value of PROSAIL model

2.1.3 基于光谱特征的枯草初级筛选

图2为试验场夏季(8月30日)绿草和冬季(11月27日)枯草样方经预处理后的平均光谱。 从图中可以看出，高寒冬季枯草与绿草光谱在可见光与近红外波段存在着显著差别。 绿草光谱表现为典型的绿色植被光谱特征，红光波段(650～680 nm)的吸收谷与近红外波段(760～1 300 nm)的高反射特征清晰。 然而，枯草的光谱特征在短波红外波段前则明显不同于绿草，其反射光谱曲线自400～1 300 nm基本呈明显的线性增加趋势，绿色植被的蓝光与红光波段的吸收谷特征完全消失，近红外波段较一致的高反射率特征被逐渐增加的线性分布特征代替。 反映了牧草干枯、叶绿素流失、叶片内部结构破坏后的独特光谱特征。

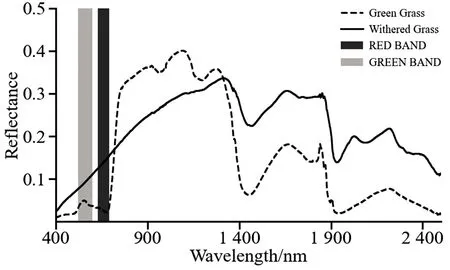
图2 海北试验场8月30日和11月27日样方平均光谱Fig.2 The average spectrum for all samples on August 30and December 30 respectively in Haibei

由于模型设定的参数阈值范围较宽且输入参数随机组合，PROSAIL模型生成的15 000组模拟光谱序列中，存在着反映绿草特征以及由绿至枯过渡阶段特征甚至“错误”的光谱。 因此，需要依据枯草的光谱特征，进行非枯草特征光谱数据的筛选排除。

观察图2可以发现，枯草在可见光波段与绿草有显著光谱差异，尤其是红光波段吸收谷的存在与否，可作为绿/枯草区分与判别划界依据。 由于绿草红光波段吸收谷与绿光波段小反射峰的存在，绿草绿光波段反射值必定大于红光波段，而枯草则是红光波段大于绿光。 因此，模拟结果中枯草光谱的筛选可通过式(3)判别

Rred-Rgreen>0

(3)

式(3)中：Rred为红光波段，本研究选取660 nm反射率；Rgreen为绿光波段，选取560 nm反射率。

当该式计算值大于0时，视该模拟光谱值反映了枯草光谱特征。 以此完成15 000组模拟数据的初级筛选, 并得到枯草相关光谱序列。

2.1.4 基于线性拟合的枯草光谱二级筛选

根据图2枯草光谱特征，枯草与绿草光谱在1 300～2 500 nm波段虽然数值差异较大，但波谱特征相似，难以区分，而在400～1 300 nm波段二者间数值与分布特征均有显著差异。

此外，图1中1 300～2 500 nm波段枯草光谱分布区间分散，最大值与最小值的极值分布区间宽，与非枯草地物光谱区间重叠范围较大。 而400～1 300 nm波段，枯草的极值分布区间窄而收敛性强，波形特征与其他地物具有显著差异性。 同时，该波段处于大气窗口，也不属于水汽的强吸收带，受水汽的影响较小。 因此从枯草400～1 300 nm波段波形特征出发，进一步区分枯草光谱。

从经过数据预处理后400～1 300 nm波段实测枯草反射光谱可以发现(图3)，这一区间枯草光谱呈准线性分布，波形线性特征显著。 对这一区间内实测光谱数据序列的线性拟合结果表明，绝大多数观测样本线性拟合方程的决定系数R2达到了99%置信区间，所有23个观测样本的线性拟合R2均通过95%置信区间。 因此，以400～1 300 nm区间模拟光谱数据序列线性拟合方程系数R2>0.95作为枯草光谱二级筛选的方法与阈值。

图3 经预处理的400～1 300 nm波段实测枯草光谱Fig.3 The measured spectrum of withered grass from400 to 1 300 nm after data preprocessing

2.1.5 枯草光谱分布区间模拟

根据式(3)及2.1.4中提出的线性拟合方法，对PROSAIL模拟输出的15 000组数据分步进行枯草光谱筛选，最终得到1 799条完成两级筛选符合枯草特征的光谱数据序列。 挑出这些序列中的最大值与最小值，构建完成400～2 500 nm枯草模拟光谱最大值、最小值与实测平均值光谱数据序列(图4)。

该最大与最小值指示了指定波段枯草反射光谱响应的阈值区间。 在400 nm处光谱反射率在0.01～0.02波动，差距微小；1 300 nm处其极值变动区间在0.24～0.42，阈值变幅0.18，而在1 450 nm水分强吸收谷波动在0.12～0.27。

从400～2 500 nm的全光谱序列变化特征看，模拟光谱与平均实测光谱显著相似。 对筛选得到的模拟光谱与平均实测光谱进行拟合评价，其R2值在0.904～0.994之间，通过了0.01显著性水平检验。 说明PROSAIL模型模拟冬季高寒牧草的效果准确可信，筛选出的模拟光谱及对应参数可用于枯草特征分析。

图4 二级筛选得到的枯草模拟光谱序列极值

2.2 模型敏感性分析

采用EFAST方法进行全局敏感性分析，将2.1.2中的参数输入组合对和产生的模拟光谱结果输入EFAST分析得到各输入参数的敏感性指数值。

图5为10个枯草性状参数在400～2 500 nm的全局敏感性指数百分比面积堆叠曲线。 从图5可以看出： 在VIS波段(400～700 nm)，LAI，LAD和Cab对枯草光谱影响较大。 在NIR波段(700～1 350 nm)，Cm和LAD平均叶倾角影响显著，影响幅度均接近50%，而在这一波段N也有持续少量影响，值得注意的是，Cbrown仅在700～800 nm之间有近40%的影响。 在SWIR波段(1 350～2 500 nm)，主要影响因素依次为Cm，LAI，Cw及LAD。 其中Cm除了在两个水分吸收带指数值较低外，其余波段均维持在50%左右，Cw则仅对两个典型水分吸收谷(1 450，1 940 nm)有突出影响，LAD的影响程度则随波长逐渐变小。

需要注意的是，虽然枯草内Cab含量非常低，是枯草低敏感参数，但由于其在牧草衰落过程中具有直接指示意义，在此也将其划入高敏感性参数。

根据以上分析结果，将输入参数分为高敏感性参数(LAI，LAD，Cm，Cab，Cw)和低敏感性参数(Cbr，Car，Cant，N，Hspot)。 通过优化高敏感性参数的取值范围，获得参数合理阈值区间。 由于低敏感性参数对模型输出的影响较小，几乎可以忽略不计，将低敏感性参数的取值固定，取值为筛选出的模拟枯草光谱序列对应的参数平均值。

参照图4枯草光谱极值分布范围，基于敏感性分析结果，分别统计5个枯草敏感参数的光谱值区间内数值分布，准确界定其数值分布范围，逼近理想阈值区间的同时，实现了模型初始运行时相对宽泛阈值区间的缩小与优化。

枯草参数敏感性分析优化的结果如表2所示。 从表2与表1的对比可以看出，LAI由0.2～2.5变动区间缩小至0.2～1.5，说明枯草叶面积指数最高阈值界限低于绿色植被的同时，其阈值范围明显偏窄。 同样，LAD的下限阈值由0提高到11，Cab的阈值范围由0～35缩窄聚集至0.03～25。 枯草敏感的5个参数阈值区间得到了较精准化的界定，为最终实现枯草参数率定进一步缩小了范围。

2.3 模型不确定性分析

由1.3.3可知，耦合关系指数可指示模型各参数间耦合作用的强弱，籍此判断各输出参数随其他参数变化而波动的不确定性。

表2指出LAI，LAD与Cw耦合关系指数值均超过了100，表明这3个参数的耦合关系强，其取值易受其他参数的影响。 因此，在反演时不能简单地将三者看作独立变量进行分析，需考虑该参数和其他参数的耦合关系带来的不确定性影响。 其他7个参数的耦合关系指数值较低，表明模型获得的参数的不确定性较小、可靠性高。

2.4 枯草关键参数阈值率定

基于表2枯草参数阈值范围，对5个高敏感性参数再次进行OFTA[15](one factorata time)局部敏感性分析。 即： 通过固定模型内所有其他参数取值，以均匀步长对表2中该参数阈值区间一一取值，逐一判别单个参数变化对模拟结果的贡献。 并以余弦距离作为评价函数，以99%置信度为标准，对比不同取值下的模拟反射光谱与实测反射光谱间的余弦距离，识别出单个参数与枯草取值方向的一致性程度及数值敏感区间，实现高敏感性参数的进一步率定，结果如表3所示。

表3 枯草关键参数取值区间参考表Table 3 Reference table for 10 main parameters threshed of withered grass

3 结 论

利用PROSAIL辐射传输模型，结合实测光谱与枯草性状参数，进行枯草反射光谱模拟，以余弦距离作为评价函数，率定了10个枯草性状参数阈值。 模拟结果显示，400～2 500 nm的全光谱模拟序列与实测光谱R2通过了0.01显著性水平检验，证实PROSAIL模型对高寒冬季枯草具有很好的模拟能力。 并依据红光与绿光波段反射率差值和顾及水汽吸收影响下枯草在400～1 300 nm的准线性波形特征提出了一种有效筛选枯草光谱的方法。

通过对模拟结果的两级敏感性分析与不确定分析，筛选出叶面积指数、叶倾角、干物质、等效水厚度、叶绿素含量等5个枯草变化高敏感参数，指出了枯草参数不确定性响应程度。 进一步，给出了不敏感性参数的推荐数值，界定了枯草敏感的LAI的阈值介于0.2～0.89、LAD为11°～90°、Cab为0～1.29 μg·cm-2、Cw为0.000 1～0.005 cm，Cm为0.008～0.05 g·cm-2，完成了高寒枯草参数率定。 为提高对高寒冬季枯草的基础认识及遥感反演等研究提供基础数据与依据。