金属纳米球-纳米圆盘结构中表面等离激元共振模式的电磁场增强研究

李梦君，方 晖

1. 唐山师范学院物理科学与技术学院，河北 唐山 063000 2. 深圳大学微纳光电子学研究院/纳米光子学研究中心，深圳市微尺度光信息技术重点实验室，广东 深圳 518060

引 言

表面等离激元(surface plasmon polariton, SPP)是自由电子在界面处发生集体相干振荡时形成的一种特殊的表面波，该表面波可存在于金属(如金、银、铜、铝、碱金属、钯、铂以及合金等)、重掺杂半导体以及一些二维材料[1]等材料中，其中以贵金属金和银最为人们所熟知，被视为研究SPP常见的理想材料[2]，因为贵金属一般都具有较大的自由电子数密度，是影响SPP丰富特性的首要因素。 除此之外，SPP的特性(如共振频率、强度等)还与金属的形貌和结构密切相关。 以金属纳米颗粒为代表的金属纳米结构其几何尺寸非常小，内部包含的原子个数大约仅为102～104个，且表面原子数随其尺寸的减小而迅速增加，从而形成表面原子数比例较高的金属纳米结构。 位于金属纳米颗粒上的SPP即局域表面等离激元(localized surface plasmon polariton, LSPP)在外界光场的激发下可表现出比较显著的表面电场增强，该局域表面电场增强被广泛应用于诸多研究领域中，如荧光[3]、拉曼散射、非线性光学[4]、光热转换[5]、光声效应、催化以及光伏转换[6-7]等。 因此精密设计金属纳米颗粒的形貌和结构来有效地调控LSPP的性质特别是局域表面电场增强就显得尤为重要，目前常用的金属纳米结构有： 具有尖角/尖端/边缘的金属纳米颗粒或具有纳米量级间隙的金属纳米颗粒聚集体等。

根据经典电磁理论人们发现，自然界中还未发现一种天然材料对外界入射的高频电磁波中的磁场产生响应，即找不到一种材料在同一波段同时具有负的介电常数和磁导率，所以一般认为其相对磁导率为1。 而早在1968年，有研究者就曾提出负折射率材料的假设，但一直没有取得研究进展。 直到2005年，人们通过对金属纳米结构及其对称性的设计与优化，可使金属纳米结构对外界入射电磁波的激发产生很强的磁响应，即磁表面等离激元(magnetic surface plasmon polariton, MSPP)[8]。 负折射率材料相对于天然材料具有很多特异性质，如反常多普勒效应、隐身、突破亚波长分辨率成像的衍射极限等[9]，可以对物理学、光学、化学和材料学等领域的研究产生深远的影响；MSPP还可以为数据存储、亚波长结构波导、光镊、生物传感器[10]以及太阳能电池等领域提供新的契机。 基于LSPP的强局域表面电场的约束作用，入射光的能量被限制在亚波长、深亚波长甚至是纳米尺度的范围内。 同理，在纳米量级范围内实现磁场的增强也逐渐成为了人们十分关注的问题。 目前实现磁场增强的金属纳米结构有： 周期性金属纳米结构(如金属纳米颗粒对阵列[11])或金属纳米颗粒多聚体[12]等。

由以上论述可以看出，具有间隙结构的金属纳米多颗粒能同时实现局域表面电场和磁场的增强，因此通过对该结构的设计和调控，可以有效地提高局域表面电场和磁场的增强因子。 本文在前期研究工作[13]的基础之上，舍去金属纳米球-薄膜结构，选择金属纳米球-纳米圆盘结构间隙处的新型表面等离激元共振模式继续进行研究，得出金属纳米球-纳米圆盘结构在单束紧聚焦径向偏振光的激发下，影响局域表面电场和磁场增强因子的因素，说明本文提出的新型金属纳米结构既在电磁场增强方面相对于已有的金属纳米结构具有一定的优势，又能丰富金属纳米颗粒SPP的理论、实验研究和广泛应用，并为后续的进一步深入研究提供一定的参考和基础。

1 实验部分

为了使研究对象更接近于实际实验和广泛应用，本文对文献[13]中的研究对象进行了改进，将两束同轴反向传播的径向偏振光改为单束沿z轴正向传播的紧聚焦径向偏振光，其电场和磁场振幅与入射光波长的变化曲线如图1所示。 从图1(a)和(b)可以看出，经过紧聚焦的径向偏振光在光轴上沿光传播方向出现了相对于径向电场分量较强的轴向电场分量，但从图1(c)可知，光轴上角向磁场的强度则相对比较微弱，这也正是有些研究领域中忽略入射光中磁场的影响的原因之一。

采用Comsol Multiphysics软件模拟计算的金属纳米结构如图2所示，圆盘半径为600 nm，厚度为10 nm，球半径为50 nm，盘和球的间距为5 nm，为了视觉效果，图中盘的厚度扩大了10倍。 由于该结构和入射激发光都具有二维旋转轴对称性，因此本文只显示某一旋转平面上的计算结果，如图中红色方框所示。 本文中金属纳米结构的材料为金(对于银材料，其原理、计算过程、结果分析以及结论基本相同，故此处不再赘述)，介电常数取自普遍被采用的文献[14]中的结果，磁导率为μ0；为简单起见，金属纳米结构周围的介质设为真空。

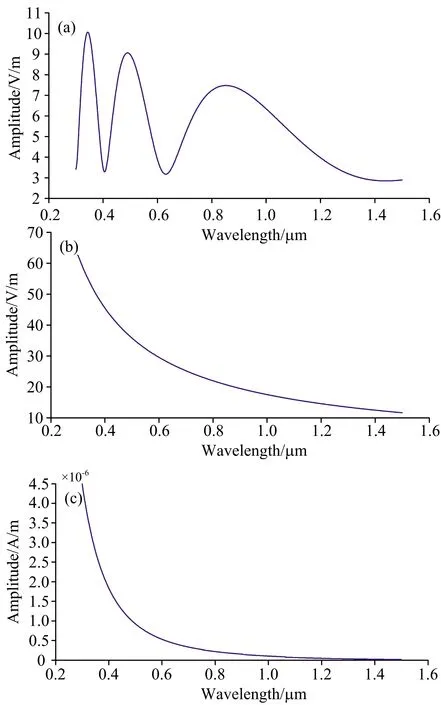
图1 入射光电、磁场振幅变化曲线(a)： (602, 5) nm处电场振幅曲线； (b)： (0, 7) nm处电场振幅曲线； (c)： (0, 7) nm处磁场振幅曲线Fig.1 Amplitude curves of electromagneticfield in incident light(a)： Amplitude curve of electric field at (602, 5) nm; (b)： Amplitude curve of electric field at (0, 7) nm; (c)： Amplitude curve of magnetic field at (0, 7) nm

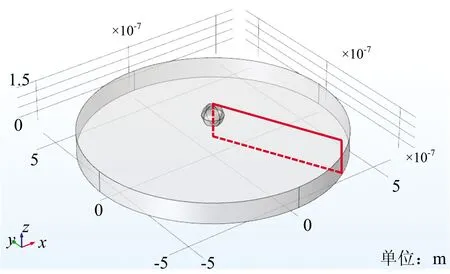
图2 模拟计算中的金属纳米结构Fig.2 Metal nanostructures studied in the simulation

2 结果与讨论

2.1 对金属纳米球-纳米圆盘结构近表面电场的分析

本文首先计算了金属纳米球-纳米圆盘结构的近表面电场随入射光波长的变化，探测点仍位于(r,z)=(0, 7) nm处，图3(a)，(b)和(c)分别为该结构的近表面电场振幅、增强因子以及相位的模拟计算结果。 从图3(a)中可以看出，金属纳米球-纳米圆盘结构的近表面电场振幅的最大值相对于文献[13]中的结果提高了近50倍左右；由图3(b)的近表面电场增强因子曲线可知，金属纳米球-纳米圆盘结构的近表面电场增强因子的最大值是文献[13]中结果的接近2倍；此外在图3(a)和(b)中，两条曲线都显示出了三个比较明显的共振峰，分别位于600，650和720 nm处，此共振峰相对于文献[13]中的结果都有了一定的蓝移，而在波长为400和900 nm处，近表面电场振幅/增强因子曲线看似比较平缓，实际上此处应为两个相对较低的共振峰，因为在图3(c)中，波长为400和900 nm时，近表面电场的相位出现了突变。 另外，从图3(c)中还可以看出，图中共有7个近表面电场的相位突变，因此不管是近表面电场振幅曲线还是增强因子曲线，都应有7个共振峰，由于近表面电场相位的变化比其振幅/增强因子的变化要快，故只能在图3(a)和(b)中观察到5个共振峰，而位于近紫外区域的2个共振峰则被400 nm处的共振峰所掩盖。

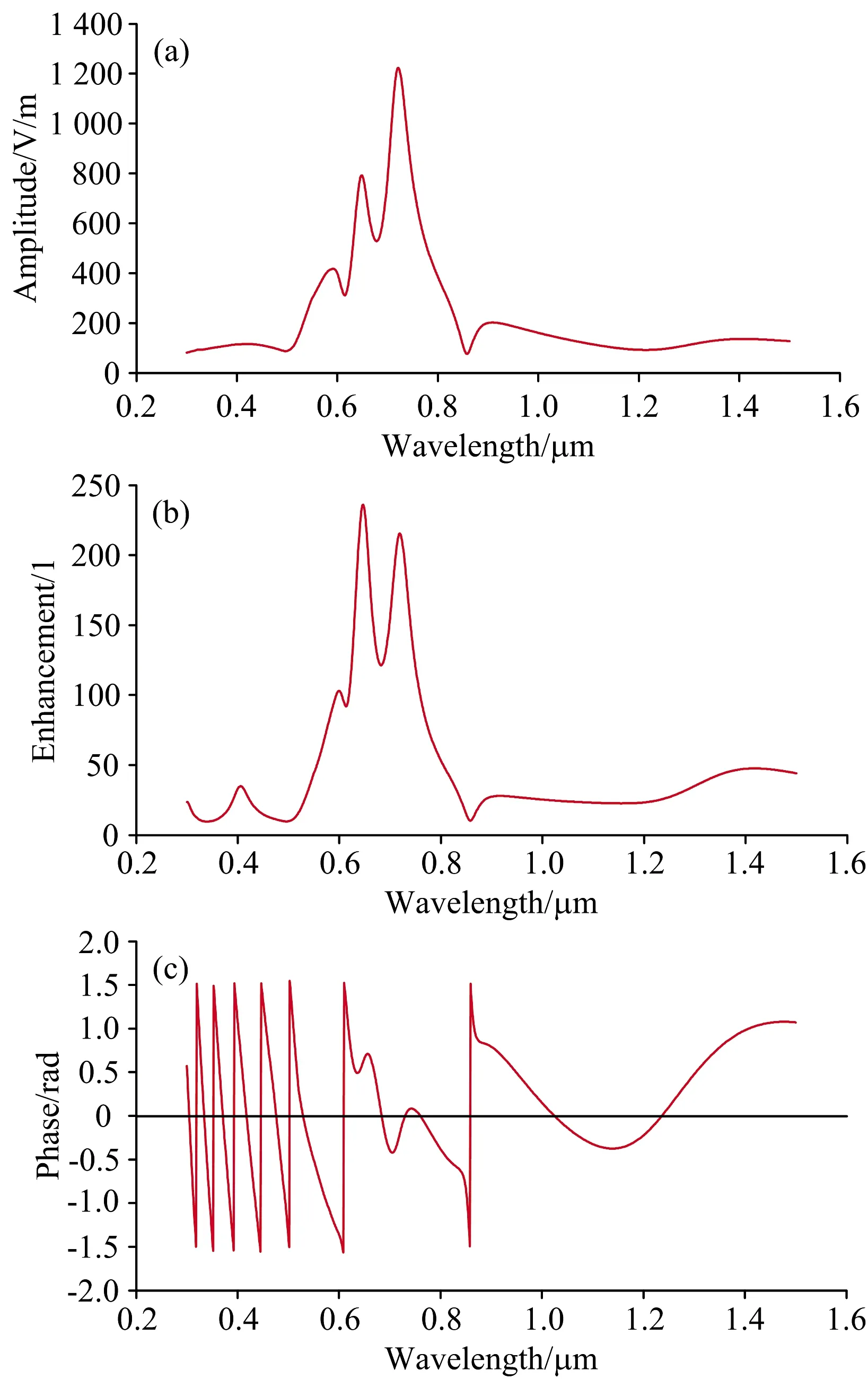
图3 近表面电场激发情况(a)： 振幅；(b)： 增强因子；(c)： 相位Fig.3 Stimulations of near surface electric field(a)： Amplitude; (b)： Enhancement; (c)： Phase

值得注意的是图3中每个共振峰各对应着一种LSPP呼吸模式[13]。 当外界激发光入射到金属纳米圆盘上时，入射光中的径向电场分量在圆盘上激发出LSPP呼吸模式，使得圆盘轴线上聚集了一定量的电子，产生了比较强的纵向电场分量；此外，入射光中的轴向电场分量也在圆盘上下表面处激发出电偶极矩，这使得圆盘轴线上的电子数量进一步增加，从而使纵向电场分量进一步得到增强。 此时金属纳米圆盘和金属纳米球的LSPP电偶极矩模式相互耦合形成了间隙模式，当两者的能量相近时，间隙处的共振耦合作用得到加强，从而得到更强的纵向电场分量。 此外，对近表面电场振幅/增强因子平方即可推知光谱结果，可以看到本文提出的金属纳米结构的共振波长可覆盖近红外至近紫外区域，具有较宽的频谱波段，显示出了该结构在近表面电场调控(强度和共振波长)方面具有一定的优越性。

为了更直观地展示金属纳米球-纳米圆盘结构的近表面电场增强分布，本文选取入射光波长分别为600，650和720 nm时即在共振峰处间隙结构处的近表面电场激发情况，如图4(a)，(b)和(c)所示，其中不同颜色代表了近表面电场振幅的增强，而黑色箭头则显示了纵向电场分量的增强，其中图4(a)显示的为虚部；图4(b)和(c)显示的为实部。 从图中可以看出，在金属纳米圆盘与金属纳米球产生共振时，间隙结构处的局域近表面电场得到了成百倍的增强，尤其是在650nm处，增强因子高达250倍左右；且入射光的能量大部分聚集于此，从而形成所谓的高能量密度的“热点”，可以显著地增强各种光与物质的相互作用过程[15]。

图4 共振波长处的近表面电场分布(a)： 600 nm；(b)： 650 nm；(c)： 720 nmFig.4 Distributions of near surface electricfield at resonant wavelength(a)： 600 nm；(b)： 650 nm；(c)： 720 nm

2.2 对金属纳米球-纳米圆盘结构近表面磁场的分析

与由金属纳米圆盘边缘处径向偏振光的电场激发金属纳米圆盘上LSPP呼吸模式不同，间隙结构处的近表面磁场则是由探测点处的入射光中的磁场激发产生，因此本文取探测点处的入射激发光来做计算，图5(a)，(b)和(c)分别为该结构的近表面磁场振幅、增强因子以及相位的模拟计算结果。 从图5(a)可以看出，金属纳米球-纳米圆盘结构的近表面磁场振幅在10-5量级左右，而入射光中的磁场振幅则在10-6量级左右(见图1(c))，由此可知，激发光在入射到间隙结构处时，不仅近表面电场得到了增强，近表面磁场也得到了一定的增强，其增强因子曲线如图5(b)所示。 由图5(b)可知，金属纳米球-纳米圆盘结构的近表面磁场增强因子的最大值已达到170倍，表现出了一定的增强优势。 此外在图5(a)和(b)中，两条曲线都显示出了四个不同的共振峰，分别位于590，650，720和900 nm处。 与近表面电场增强因子曲线相比，图3(b)中650和720 nm处两个峰的峰值较高，而图5(b)中只有720 nm处的峰值较高。 另外，从图5(c)中还可以看出，图中共有8个近表面磁场的相位突变，因此不管是近表面磁场振幅曲线还是增强因子曲线，都应有8个共振峰，由于相位的变化要快于振幅/增强因子的变化，故只能在图5(a)和(b)中观察到4个共振峰，而位于近紫外区域的3个共振峰应该是被波长更短处的共振峰所掩盖，位于近红外区域的1个共振峰应该是被波长更长处的共振峰所掩盖。

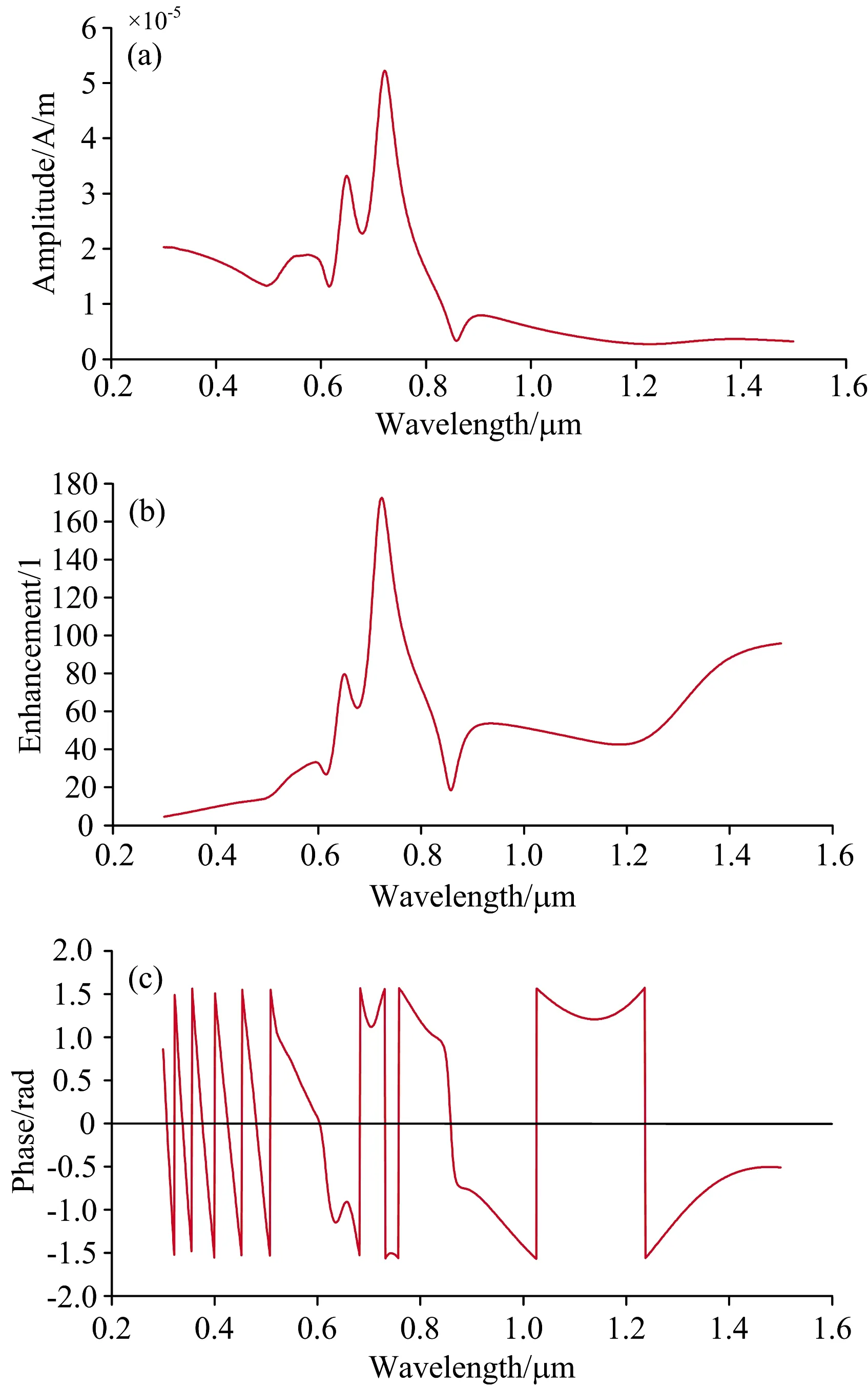
图5 近表面磁场激发情况(a)： 振幅；(b)： 增强因子；(c)： 相位Fig.5 Stimulations of near surface magnetic field(a)： Amplitude; (b)： Enhancement; (c)： Phase

为了更直观地展示金属纳米球-纳米圆盘结构的近表面磁场分布，本文选取在近表面电场增强时的共振波长间隙结构处的近表面磁场激发情况，如图6(a)，(b)和(c)所示，其中不同颜色代表了近表面磁场的振幅，而黑色箭头则显示了角向磁场的分布(由于磁场方向垂直于rz平面，故显示三维图形)，三个图显示的均为虚部。 从图中可以看出，探测点(r,z)=(0，7) nm处的磁场振幅相当于(r,z)=(30，7) nm处磁场振幅的10-3倍左右，但其增强因子的最大值确是后者的接近7倍，显示出了一定的近表面磁场的增强优势。 此外，从图6还可以看出，随着入射光波长的增加，不仅近表面磁场的振幅/增强因子随之增加，而且入射光的能量越来越向间隙结构附近处集中，从而实现近表面磁场的局域化。

图6 共振波长处的近表面磁场分布(a)： 600 nm；(b)： 650 nm；(c)： 720 nmFig.6 Distributions of near surface magneticfield at resonant wavelength(a)： 600 nm；(b)： 650 nm；(c)： 720 nm

2.3 金属纳米球-纳米圆盘结构近表面电、磁场共振波长分布的对比

本文列出了金属纳米球-纳米圆盘结构在单束紧聚焦径向偏振光正入射情况下的近表面电、磁场共振波长分布，如表1所示。 从表中的相互比较可以看出，金属纳米球-纳米圆盘结构的近表面电、磁场出现增强时，其入射光波长基本上都比较接近，有些情况下则完全相同(如900 nm处)。 由此可以看出，在共振波长处(或附近)，本文提出的金属纳米结构可以同时实现近表面电、磁场的增强，展示出了一定的近场增强优势。

表1 近表面电、磁场共振波长对比Table 1 Comparison of resonant wavelength of near surface electromagnetic field

3 结 论

模拟计算结果表明，金属纳米球-纳米圆盘结构在单束紧聚焦径向偏振光的激发下会产生LSPP和MSPP近表面电、磁场的增强： 近表面电场的增强因子高达250倍；近表面磁场的增强因子高达170倍，显示出了非常好的近场增强优势。 但也应该看到，本文提出的金属纳米结构的近表面磁场增强因子相对于已经报道的金属纳米结构(即金属纳米颗粒对阵列)还有一定的差距，如何进一步设计、优化金属纳米结构来同时提高近表面电、磁场的增强因子将是下一步的研究目标。 此外，如何将金属纳米结构的近表面电、磁场增强应用于生物医学领域更是接下来长期的研究目标，也希望本文及以后的研究结果能为人们抗击疫情提供一份微薄之力。