优化光谱指数建立水稻叶片SPAD的高光谱反演模型

于 跃，于海业，李晓凯，王洪健，刘 爽，张 蕾，隋媛媛

吉林大学生物与农业工程学院，吉林 长春 130022

引 言

叶绿素作为植物光合作用的重要色素，其含量、分布和变化可以直接或间接反映植物的光合能力、养分状况和生长健康状况。 精确诊断叶绿素含量对农作物的长势监测、营养诊断、作物估产以及病虫害预警等科学管理具有重要意义。 水稻是我国重要粮食作物。 吉林省地处水稻生产的“黄金带”，主要品种为粳稻，一年一季，7月中旬起水稻分蘖期结束，陆续进入拔节孕穗期，该生育期是水稻从长根、长叶、长蘖等以分蘖为中心的营养生长期开始进入以幼穗发育为中心的生殖生长期的关键转折期，此时水稻叶片中的叶绿素含量直接影响光合强度和有机物的积累量，进而影响幼穗的发育以及水稻的产量。 因此，对拔节孕穗期水稻叶绿素含量的研究具有一定的现实意义。

目前，利用光谱指数反演植被叶绿素含量是十分有效的方法[1]。 构建光谱指数是为了提取光谱中与叶绿素含量构成较高相关性的信息，一般将特定波段对应的反射率进行组合计算，而特定波段的选择通常需要参照一定的物理基础。 最初Horler等将绿色植被670～780 nm波段范围内特征曲线的一阶导数最大值定义为“红边”，对应的物理含义为红光波段对叶绿素强烈吸收的峰值位置，并认为植被冠层光谱“红边”位置与叶绿素含量之间可能存在密切的联系；Curran等通过“红边”位置与植被冠层总叶绿素含量敏感程度的研究对这一结论进行了佐证[2]。 随后一些学者利用该波段范围内一些关键波段的组合运算建立了一系列光谱指数，如比值植被指数(ratio vegetation index，RVI)、差值植被指数(difference vegetation index，DVI)[3]、归一化植被指数(normalized difference vegetation index，NDVI)[4]等，放大了光谱反射率与植被叶绿素含量之间的联系。 随着对叶绿素含量反演研究的深入，一些学者发现，基于“红边”位置范围内关键波段组合获得的光谱指数由于仅包含两个或三个波段的运算，相对于完整的光谱反射率特征曲线，所包含的有效信息十分有限，将这些光谱指数应用于不同品种、生长时期、地点等因素影响下的作物中时，计算出来的结果可能与真实情况具有较大的偏差。 因此，一些学者提出了积分指数的概念，综合更多的敏感波长以增加光谱指数的适用性。 Oppelt和Mauser等计算了玉米反射率光谱600～735 nm范围内两点积分运算的面积与包络线的比值，称之为叶绿素吸收积分指数(chlorophyll absorption intergral, CAI)[5]，探究了该指数对玉米叶面积指数和冠层叶绿素密度的预测能力，并分析了该指数对冠层结构、光照几何、土壤背景反射率和大气条件的敏感性；Delegido等为研究处于复杂环境中的城市植被叶绿素的空间分布建立了反射率曲线归一化面积指数(normalized area over reflectance curve，NAOC)[6]，利用该指数对梧桐、枣椰等多种绿色植被的叶绿素含量进行反演，发现NAOC指数对于绿色植被的叶绿素含量有着较强的反演能力，并通过NAOC指数与叶片叶绿素含量之间的线性拟合提供了一种遥感估测植被叶片叶绿素的简便方法。 但是该光谱指数对于农田环境下拔节孕穗期水稻的叶绿素含量是否同样具有较强的预测能力还有待探究。

通过将NAOC光谱指数定义的积分计算简化为基于积分限(a，b)即双波段组合运算的方式进行优化，并利用相关分析法筛选出原始光谱和三种数学变换光谱中与水稻叶片SPAD具有较高相关系数的特征波段组合，将计算得到的优化光谱和变换光谱指数用于构建拔节孕穗期水稻叶片SPAD的反演模型，最后对比分析三种建模方法的精度及稳定性，确定基于优化光谱和变换光谱指数建立的水稻叶片SPAD最优反演模型。

1 实验部分

1.1 试验区概况与数据采集

试验于2019年7月28日在长春市双阳区(43°30′E，125°39′N，平均海拔234.3 m)良种繁育场水稻种植基地进行。 供试品种为吉粳509，一年一季稻。 试验当日晴朗无风，于上午10：00至下午14：00进行水稻生理信息的获取。 测量时，选择10株生长状况良好、长势较为接近的水稻植株分别进行编号；在目标叶片的选取过程中，参考水稻生育进程的叶龄模式，统一选择叶面积较大的叶片即主茎第七、八片叶(也称倒二叶、倒三叶)作为数据获取目标，采集原始样本共20组。 采集的数据包括水稻目标叶片高光谱和叶绿素含量： (1)目标叶片高光谱采用Analytical Spectral Devices分析光谱仪器公司生产的HandHeld 2手持式地物光谱仪进行测量，该仪器的光谱波段范围为325～1 075 nm，采样间隔为1.4 nm，分辨率为3 nm@700 nm。 使用前预热20 min，每个叶片获取3条光谱曲线，每次测量后均使用白板校正。 (2)叶绿素含量： 选取日本产SPAD-502叶绿素仪同步获取对应水稻叶片的叶绿素相对含量。 所测得的SPAD值虽然不能代表叶片真实的叶绿素含量，但考虑到该叶绿素仪具有显著的便携性和无损检测的特质，且已有研究表明两组数值之间存在明显的正相关关系，因此使用SPAD值近似替代水稻叶片的真实叶绿素含量。 测量时需避开主叶脉，从叶尖到叶尾等间隔标记五个点，每个点测量一次，重复测量5次后取其平均值作为该叶片叶绿素含量的测量值。

1.2 光谱数据预处理

为了避免环境噪声的干扰，需要对原始光谱曲线进行预处理。 由于小波分析具有放大微小信号变化的特性，因此常用于捕捉作物对重金属污染、胁迫等极端条件的微弱响应[7]。 有研究表明小波分析法能够把对水稻原始光谱信号有影响的因素进行有效的排除，如背景影响、设备工作时产生的噪声影响以及大气的散射、反射和吸收等[8]。 小波分析由傅里叶分析衍生而来，其优点是可以将信号从时域和频域两个维度进行分解，通过对小波母函数的缩放平移运算来实现噪声剔除和信号局部特征的细化，有效保护原始信号中的尖峰信号和突变信号。 在原始光谱信号中，信号的主要特征保留在低频部分，信号的细节和噪声主要分布在高频部分。 小波分析正是通过设定阈值的方式保留低频部分的主要信号特征，在高频部分筛选有效信息，实现噪声剔除的目的[9]。 对分解、筛选后的低频部分和高频部分信号进行融合和重构，获得去噪后的光谱反射率曲线。

1.3 优化光谱指数NAOC

NAOC指数是一种包含多个光谱带的积分光谱指数，其物理含义如图1所示。a和b为光谱曲线中600～800 nm之间分别位于670 nm波段两侧的两个点，NAOC则代表黄色区域与整个矩形区域面积的比值。 NAOC指数定义为

(1)

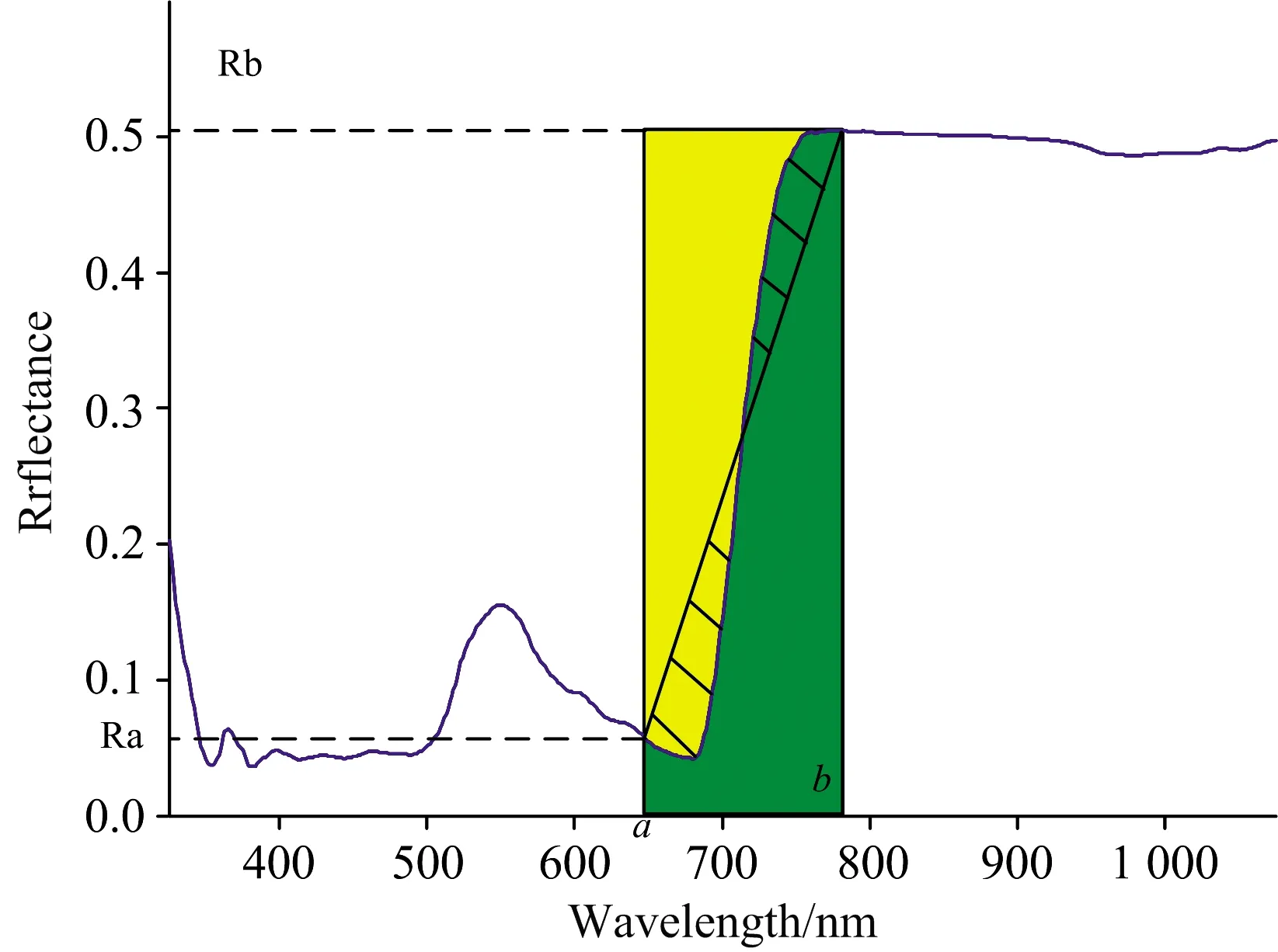
图1 NAOC光谱指数示意图Fig.1 Diagram of NAOC spectral index

有学者针对NAOC指数的变量降维和运算简化提出了优化策略。 Facundo Carmona等通过对位于红边波段的两个阴影部分面积做近似处理，将原始公式中积分运算得到的绿色区域面积简化为直角梯形的面积，原始NAOC指数所表示的黄色区域与矩形区域面积比即可简化为除去该直角梯形后剩余的三角形与矩形的面积比[10]。 将其定义为

(2)

此时，光谱指数的数值完全取决于积分限(a，b)，而a和b在原始光谱曲线中也可以看作是两个波段的组合。 因此，优化后的NAOC指数亦可看作一种基于双波段组合的简单运算光谱指数，但是所包含的有效信息却远多于其他基于双波段组合运算的光谱指数。 本工作在已有研究的基础上，着重探究优化NAOC光谱指数以及几种数学变换形式下的变换NAOC光谱指数对水稻叶片叶绿素含量的反演能力。

2 结果与讨论

2.1 基于小波分析的水稻叶片高光谱预处理

目前，小波分析可以通过Matlab2017b中小波分析工具箱快速实现。 常见的小波母函数有Harr小波，Daubechies小波和Symlet小波等，不同类型小波的对称性、正交性和紧支撑性都不相同，对于信号局部特征的描述能力也有很大的差异[11-12]。 预实验选择了结果较优的4阶Daubechies小波即db4小波对原始反射率光谱进行1～6层小波分解，结果如图2所示。 L0层为原始光谱信号，所包含的噪声较多，以上下震荡的“毛刺”形式呈现；L1—L6层为分解重构后的光谱信号，可以看出随着分解次数的不断增加，高频信号被不断地筛除，“毛刺”逐渐减少，光谱曲线趋于平滑。 当分解层数达到5～6层时，信号局部特征发生了改变，部分原始信号中的特征点出现了移位甚至变形，说明此时存在过度分解的情况。综合考虑重构光谱信号的平滑度和信噪比等因素，最终确定L4层重构光谱为原始光谱反射率曲线小波分析去噪处理的结果。

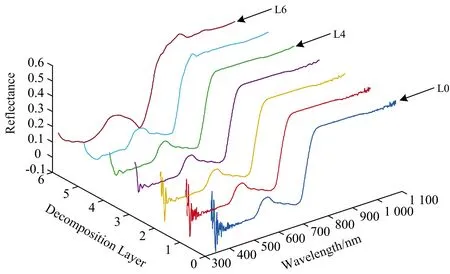
图2 小波分析L1—L6层重构反射率光谱Fig.2 Reconstructed reflectance spectra ofL1—L6 layers by wavelet analysis

2.2 优化光谱指数与水稻叶片SPAD的相关性分析

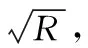
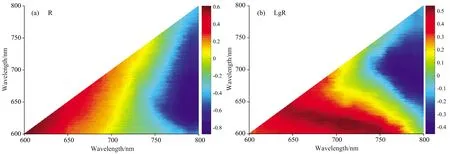
图3 优化光谱和变换光谱指数与水稻叶片SPAD相关性等势图Fig.3 Isopotential diagram of correlation coefficient between optimized and transformed spectral indices and SPAD of rice leaves

为了评价优化光谱和变换光谱指数与水稻叶片SPAD的相关程度，还选择了几种常见的基于双波段或三波段运算的光谱指数与水稻叶片SPAD进行相关性分析。 除了前文中提到的RVI、DVI和NDVI指数，还选择了绿色归一化植被指数(green normalized difference vegetation index，GNDVI)、三角形植被指数(triangle vegetation index，TVI)、土壤调节植被指数(soil-adjusted vegetation index，SAVI)、修正的叶绿素吸收率指数(modified chlorophyll absorption ratio index，MCARI)和MERIS陆地叶绿素指数(MERIS terrestrial chlorophyll index，MTCI)共计八种常用光谱指数，如表1所示列举了8种植被指数的计算公式、参考文献以及计算所得的与水稻叶片SPAD的皮尔森线性相关系数。

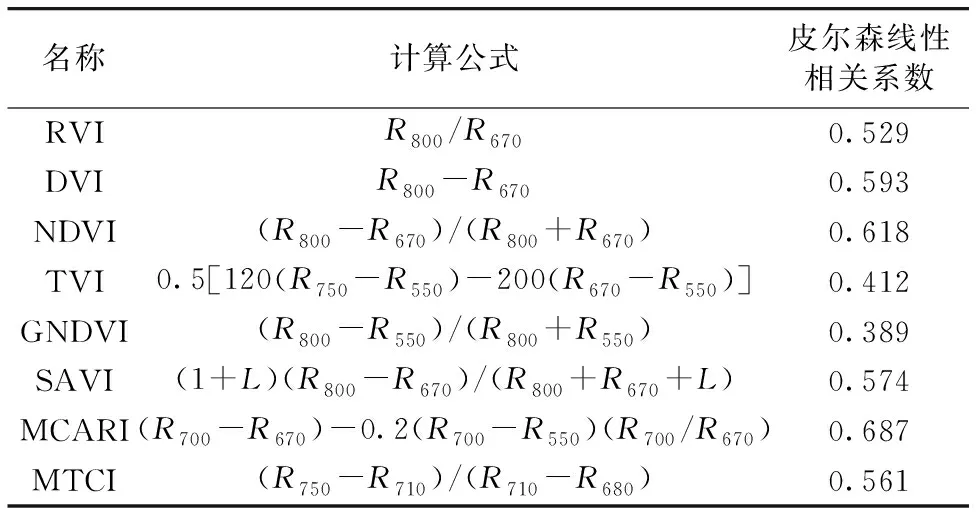
表1 八种常用双波段光谱指数及其与水稻叶片SPAD线性相关系数

表1中，L是随着植被密度变化的参数，当植被覆盖度很高时为0(此时SAVI=NDVI)。 对于L的取值，Huete指出，L取0.5时SAVI消除土壤反射率的效果最好。 因此表中L取0.5[13-14]。

从表1中相关分析的结果可以看出8种常用的基于双波段或三波段的光谱指数中与水稻叶片SPAD相关度最高的是MCARI和NDVI，相关系数分别为0.687和0.618，均小于0.7，说明本工作提出的优化光谱和变换光谱指数虽同样基于双波段组合运算，针对水稻叶片SPAD的相关性分析结果却明显优于常见的几种基于双波段组合运算的光谱指数。

2.3 基于优化光谱和变换光谱指数建立水稻叶片SPAD反演模型

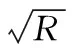
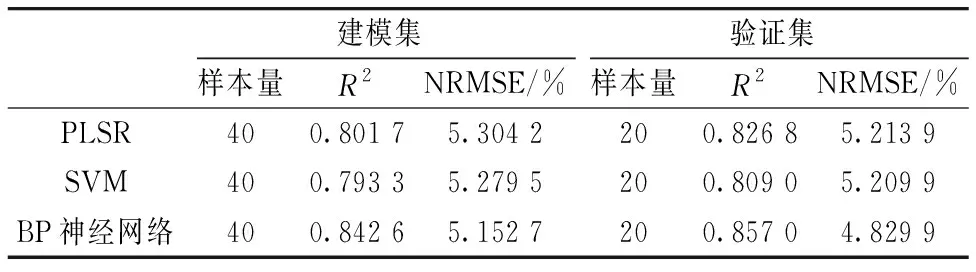
表2 三种建模方法反演结果Table 2 Inversion results of three modeling methods

由以上结果可以看出，不论是建模集还是验证集，利用优化光谱和变换光谱指数建立的三种反演模型决定系数均大于0.79，归一化均方根误差最大不超过5.4%，表明三种反演模型均能实现对水稻叶片SPAD精准预测的功能。 而三种反演模型中，采用BP神经网络方法建立的模型其验证集具有相对较高的决定系数，其值为0.857，模型拟合度相对较好；预测精度也相对较高，归一化均方根误差仅为4.829 9%。 通过建模过程中的不断尝试，确定了最佳的神经网络模型结构为3层，隐藏层节点数为6，设置学习速率为0.1，当迭代次数达900次时，神经网络模型精度趋于稳定，此时该模型对于水稻叶片SPAD的反演效果最佳。

3 结 论

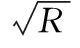
图4 预测结果散点图(a)： PLSR；(b)： SVM；(c)： BP神经网络Fig.4 Scatter plots of prediction results(a)： PLSR；(b)： SVM；(c)： BP

利用四种形式的优化光谱和变换光谱指数对应的相关系数中高于0.87的3个积分波段组合计算得到60个优化光谱指数值，按照2∶1的比例划分为建模集和验证集，建立PLSR，SVM和BP神经网络三种水稻叶片SPAD反演模型。 三种反演模型决定系数均大于0.79，归一化均方根误差小于5.4%，表明三种反演模型均能实现对水稻叶片SPAD精准预测的功能。 而三种反演模型中，BP神经网络具有最高的验证集决定系数0.857，归一化均方根误差为4.829 9%，因此，BP神经网络模型为利用优化光谱和变换光谱指数反演水稻叶片SPAD的最佳模型。

通过现有技术手段实现了水稻叶片SPAD的高光谱反演，其优点在于： (1)既保留了积分指数所包含的特定波段范围内大量的光谱信息又能以简单的四则运算代替复杂的积分运算，一定程度上提高模型效率；(2)对本文提出的优化光谱和变换光谱指数与水稻叶片SPAD建立全波段的二维相关性分析，在合理条件下可以获得最优相关系数，最大限度的保证建模参数的有效性和模型的精度。 影响拔节孕穗期水稻生长发育的因素多样且复杂，由于数据采集的局限性，只针对叶绿素含量这一单一因素的影响进行了探讨，并未考虑叶面积指数、净光合速率等其他生理信息的作用。 因此，针对多种生理信息交互作用下的综合反演研究还有待进一步探究。