破碎区至冲泻区波浪非线性特征的实验研究

邓 斌，张 雯，蒋昌波，刘晓建

(1.长沙理工大学水利与环境工程学院，湖南 长沙 410114； 2.水沙科学与水灾害防治湖南省重点实验室，湖南 长沙 410114； 3.长沙理工大学水科学与环境工程国际研究中心，湖南 长沙 410114)

0 引言

海岸动力过程是控制海岸发育和演化的主要因素，由于床面地形改变以及建筑物的影响，波浪接近海岸线过程中，波形变得极不稳定，波浪出现折射、散射、反射等现象，并在近岸破碎区发生破碎，在近岸冲泻区呈现周期性的上爬和回落[1]。在过去的几十年里，学者们通过多种方式开展波浪水动力特性的研究，针对破碎区的水动力特性，在理论、现场、实验和数模等方面取得了丰富的研究成果[2-3]。与破碎区不同，冲泻区波流运动具有非定常、非均匀、强湍动和高掺气等特点[4]，故对该区域的流动特性进行实验测量非常困难。目前，基于物理模型实验[5-6]和数值模拟方法[7-8]对冲泻区内的水动力学特性已有基本认识，但近岸波浪具有较强的非线性，导致波高的概率密度偏离正态分布，因此仍需深入研究。ALSINA et al[9]指出内破波带是破碎区与冲泻区之间的过渡边界，随机条件下难以准确划分内破波带和低冲泻区：一方面由于动力学特征差异，冲泻区不能仅仅被视为内破波带的延伸；另一方面由于两区域之间的水动力学及形态动力学相互影响，需综合研究破碎区、内破波带与冲泻区。因此综合考虑破碎区和冲泻区波浪传播的非线性特征更具现实意义。

自上世纪50年代以来，国内外不少学者对波浪非线性特征开展了深入研究：TICK[10]首次提出二阶谱的概念和表达式来研究波浪非线性，为研究波浪非线性开创了先例；LONGUET-HIGGINS et al[11]研究波动的非线性特征对海浪统计分布的影响，得出了深水海浪波面高度的非正态分布以及偏度的理论表达式；ELGAR et al[12]通过对二阶谱在整个坐标内进行积分，得出二阶谱实部和虚部分别对应波浪的偏度和不对称度；MORI et al[13]基于高阶谱法分析了高阶(二阶及以上)非线性对深水随机波列的影响；丁兴平等[14-15]通过发展二阶谱方法对海浪的非线性进行了深入研究；包伟斌[16]通过建立数值模型对波浪传播、变形和波形不对称性进行分析，研究风浪破碎波的二阶谱特征；类淑河[17]的研究结果表明二阶谱实部和虚部均可作为描述风浪破碎非线性的指标。以上关于波浪非线性的研究大多集中在离岸区或者是近岸破碎区，较少延伸到水动力特性更为复杂的冲泻区，对冲泻区的波浪非线性特征认识仍不充分。

综上可见，近岸带破碎区至冲泻区属于强非线性区域，该区域水流运动形式复杂，波浪运动规律还有待继续深入研究与探讨。本文利用物理模型水槽概化实验，基于非线性统计分析方法，探讨了实验中波浪几何形态特征以及流速的非线性规律。本研究可为深入分析破碎区至冲泻区波浪非线性特征对岸滩演变的影响机制提供参考。

1 实验布置与分析方法

1.1 实验设备与布置

实验在长沙理工大学水沙科学与水灾害防治湖南省重点实验室的PIV专用水槽中进行。水槽尺寸为20 m×0.4 m×0.5 m，空间尺度总体误差小于 1 mm，水槽两边及底面为玻璃壁面。水槽左端为封闭的溃坝装置，由2块厚2 mm的铝板构成，其中右边铝板设置为可上下移动的闸门，与水槽两侧形成一个1 m长、0.4 m宽的水库。闸门顶部与不可拉伸的细绳连接，通过滑轮后细绳另一端配重 10 kg，通过电磁开关控制闸门。闸门可在0.2 s内被完全抽起，溃坝产生的波浪在下游发生卷破，并形成高强度的涌浪和随后的冲流事件。水槽右端为 1∶10、1∶35 接 1∶10 和 1∶35 三个坡度的概化岸滩，具体是将透明玻璃安装在制作好的不锈钢架上，并用中性硅酮胶密封模型与水槽两侧的缝隙，防止水体泄漏。其中斜坡起点位于x=0 m位置。实验布置如图1所示，本实验并未完全使用到20 m，仅到11 m处。溃坝波传播过程的实验照片如图2所示，实验工况设置见表1。

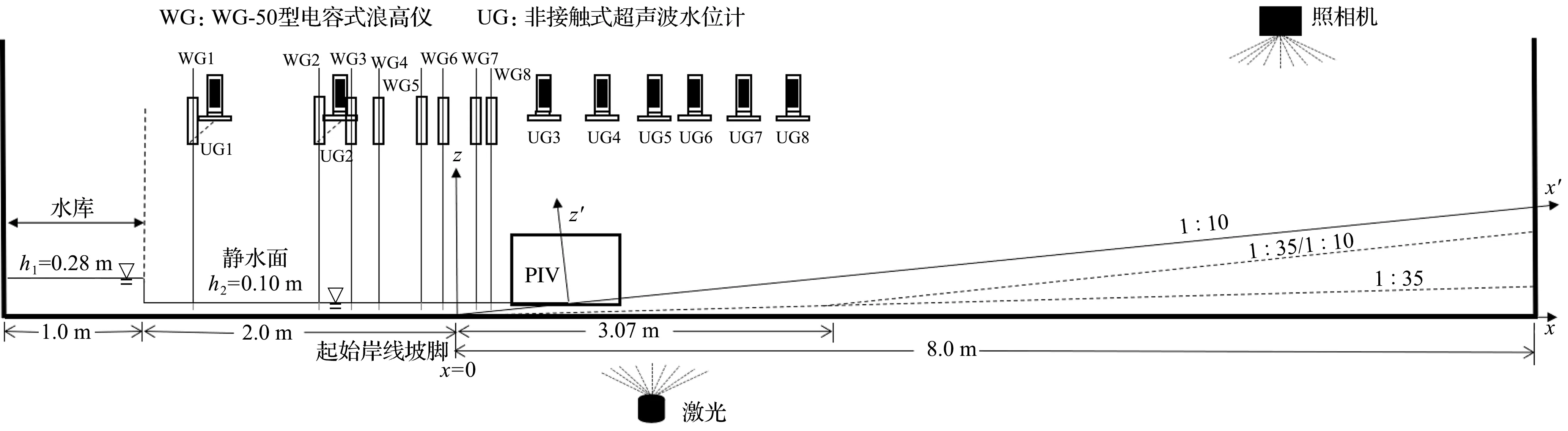
图1 实验装置布置图Fig.1 Scheme of experimental arrangement

表1 实验工况Tab.1 Study case

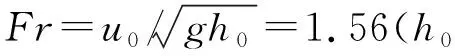
为获得破碎区至冲泻区内水位的时空变化特征，实验采用加拿大RBR公司生产的WG-50型电容式浪高仪(WG)和德国GE公司生产的非接触式超声波水位计(UG)分别测量两个区域的波高变化。其中，浪高仪的精度可达0.15%，超声波水位计测量精度达 0.2 mm。实验前，浪高仪和超声波水位计均按标准进行严格标定。实验流速测量采用美国TSI公司的粒子图像测速仪(PIV)记录流场空间结构及其流动特性，拍摄窗口尺寸为21 cm×21 cm，工况1拍摄范围为x=2.75～5.14 m，工况2拍摄范围为x=2.80～5.12 m，工况3拍摄范围为x=0.42～2.95 m。实验坐标轴以坡脚中心为起点，水流方向为x轴方向，垂直水槽边壁的方向为y轴方向，垂直底面的方向为z轴方向。沿程设置多个测量断面，波高和水位测量断面位置详见表2。

图2 溃坝波传播过程Fig.2 Propagation of dam-break wave

表2 浪高仪及超声波水位计布置位置Tab.2 Locations of wave gauge and ultrasonic water level gauge

1.2 分析方法

波浪随时间变化非线性显著，垂向和水平向不对称性较明显，通常采用高阶统计量中的无量纲系数：偏度(Skewness)、不对称度(Asymmetry)、峰度(Kurtosis)对波浪的浅化和非线性进行度量。

偏度是表示波浪沿水平轴分布对称性的统计量，用于描述波浪从波峰到波谷的不对称程度。ELGAR et al[12]提出二阶谱实部的积分对应数据分布的偏度Sk：

(1)

如果波形分布是对称的，则Sk=0；如果分布是不对称的，则Sk≠0。Sk的绝对值越大，波形沿水平轴方向分布的不对称程度也就越明显：当Sk>0时，与正态分布相比，概率密度分布曲线具有正偏态或者右偏态，峰值偏向较小值一侧，直观显示为位于均值右侧的数据比位于均值左侧的数据少；当Sk<0时，具有负偏态或者左偏态，峰值偏向较大数值一侧，直观显示为位于均值左侧的数据比位于均值右侧的数据少。

ELGAR et al[12]通过对二阶谱虚部积分得到垂直轴方向的不对称性，称为不对称度Asy：

(2)

式中:Im( )表示虚部，H是希尔伯特变换(Hilbert transform)的缩写。

Asy>0时，波浪整体沿传播方向倾斜；Asy<0时，波浪整体沿传播反方向倾斜。波浪传播到浅水区时，波浪垂直轴方向的不对称性明显。

峰度Ku又称为平滑度，是描述波浪整体分布形态相对于正态分布陡缓程度的统计量：

(3)

当Ku=3时，波浪分布形态服从正态分布；当Ku>3 时，数据分布比较集中，数据分布的高峰比正态分布更加陡峭，整体呈尖峰状；当Ku<3时，数据分布相对比较离散，形态呈扁平状。

2 实验结果及分析

2.1 正态性验证

为了验证实验中波浪分布的正态性，本文给出3种不同工况下WG7断面的Q-Q图(Quantile-Quantile Plot，简称Q-Q图，图3)。正态Q-Q图是以观测的波浪样本分位数为横坐标，以按照正态分布计算的相应理论分位数为纵坐标，不同时间序列的波高值为直角坐标系的散点。

图3 不同工况下WG7 断面Q-Q图Fig.3 Q-Q diagram of WG7 section under different cases

从图3中可以看到，数据点并不完全成一条围绕第一象限对角线的直线，说明波浪坍塌波动不符合正态分布，可用偏度、不对称度、峰度等高阶非线性参数对波浪偏离正态性的程度进行度量。

2.2 波高非线性分析

实际波浪的波面存在较大的不对称性，与正态分布有较大的偏差。接下来主要从波高的偏度、不对称度和峰度分析实验中波浪的运动形态，了解岸滩变化趋势。

2.2.1 波高的偏度

波高偏度沿程分布如图4所示：在溃坝发生后(x=-2 m 处)波浪波动剧烈，离岸位置的偏度值较大；随着波浪向岸传播，波形的概率密度分布向右侧偏离正态分布的程度减小；到达初始岸线处，Sk逐渐减小至最小值(0附近)，波形概率密度分布趋于正态分布；当波浪经过初始岸线后，波浪在岸滩上受浅化作用与岸滩作用的影响显著，波浪的偏态效果加强，波形的概率分布再次向右侧偏离正态分布。

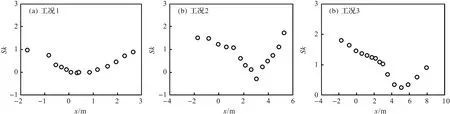
图4 不同工况下波高偏度沿程分布Fig.4 Wave height skewness distribution along the beach under different cases

在波浪坍塌破碎交界处(x=0 m附近)，3种工况下偏度值变化不大，表明偏度受波浪破碎影响较小，这与赵西增[22]的研究结果相符。同时，分布图表明在冲泻区向岸方向偏度值逐渐增大，这一现象与HENDERSON et al[23]研究相符。整体上3种工况下波浪的Sk大于0，这反映了冲泻区波浪具有波峰高且尖，波谷平且浅的特征。但是工况2中初始岸线(x=3.2 m)附近存在的波浪Sk值小于0，可体现为波形向左偏离正态分布，这说明波浪在岸滩处因与岸滩相互碰撞会产生较大变形。

2.2.2 波高的不对称度

图5是波高不对称度沿岸滩的变化情况。从图中可以看到：波浪向岸传播的过程中，水平不对称度分布基本呈现先稍微增加后减小的趋势，与偏度呈现相反的变化趋势，不对称度的最大值出现在初始岸线之前。工况1中波高的不对称度增长段出现在破碎区(x<-1 m 处)，且在初始岸线附近(x=1 m)迅速减小。工况2中波高的不对称度增长段可持续至坡脚后区域，但在x=2 m 附近迅速减小。工况3中波高的不对称度增长段持续距离远且增长斜率最大，在初始岸线附近(x=3.5 m)达到最大然后迅速减小。各工况的不对称度变化趋势表明，在不对称度增长范围内波形持续向波浪传播方向倾斜，且倾斜程度进一步加强。当波浪传播至岸滩后，波浪与岸滩的相互作用改变了波形，不对称度相比之前有所减小，但不对称度基本都大于0。这说明实验中的波浪从产生到传播至岸滩的过程中波形持续向波浪传播方向倾斜，但到达岸滩后变形程度逐渐减弱，即波浪的前倾变形在破碎区表现较强而在冲泻区表现较弱。研究表明波浪的不对称度与床面剪切力有关[24]，因此本实验中波浪的持续前倾现象将会影响岸滩的受力特性。

图5 不同工况下波高不对称度沿程分布Fig.5 Wave height asymmetry distribution along the beach under different cases

2.2.3 波高的峰度

图6为波高峰度沿程的变化情况。从图中可以看出不同工况下峰度均呈现先减小后增加的变化趋势。峰度减小段出现在初始岸线之前，峰度最大值位于x=-2 m处，此外在各工况下峰度均大于3，说明此时波高数据分布集中，波动比较剧烈，整体呈现尖峰状；峰度最小值位于初始岸线附近，峰度约为1，说明该处波高数据分布相对比较离散，波动减弱，波浪呈扁平状；当波浪到达岸滩后，与岸滩相互作用比较剧烈，波浪整体陡峭程度持续增加，波面位移关于平均水平面垂向分布不对称性加剧，峰度增大。对比3种工况下的峰度值可发现：工况1中峰度在x=-2 m 处接近3，而工况2和工况3中峰度值在x=-2 m 处均大于3，分别在坡脚和初始岸线附近才降至3，这与通过偏度分析的结果存在差异。事实上，在这些位置波形均呈现非线性，这与JHA[25]通过计算非线性随机海洋波数据所得的结果相符：偏度值随波陡呈现线性变化趋势，而峰度值则随着波陡呈现二次函数的变化趋势，波陡值往往都是小于1的数值，其平方值则更小于1，说明偏度更能体现非线性的影响。

图6 不同工况下波高峰度沿程分布Fig.6 Wave height kurtosis distribution along the beach under different cases

2.3 流速非线性分析

波浪运动是影响岸滩演变的主要因素之一，研究流速时间序列的非线性对于岸滩冲淤演变预测和防止岸滩冲刷侵蚀至关重要。近底区域流速变化过程的偏度和不对称度对泥沙输运有显著的影响[12-13]。为了解不同断面不同水深流速非线性特征的分布规律，选择各工况下分别位于回落流位置、低冲泻区、中冲泻区和高冲泻区4个断面的流速特性进行统计分析：工况1中选取了x=0.55 m、x=1.47 m、x=2.06 m 和x=2.67 m处PIV测量窗口采集的流速数据；工况2选取了x=2.80 m、x=3.28 m、x=3.88 m 和x=4.77 m处PIV测量窗口采集的流速数据；工况3选取了x=3.00 m、x=3.75 m、x=4.44 m 和x=5.00 m处PIV测量窗口采集的流速数据。

2.3.1 流速的偏度

图7是不同工况下不同断面在不同水深处流速的偏度分布，结果表明：在工况1中，溃坝波到达初始岸线之前，水体上部的流速偏度值较大；在低冲泻区流速偏度沿垂线的分布基本在0附近，接近正态分布，但在自由表面处流速偏度大于0.5；当运动至中、高冲泻区时，流速偏度值沿垂线分布散乱，正偏和负偏的情况同时存在。在工况2中各断面流速偏度分布差别较大，溃坝波到达初始岸线前流速偏度最大值可达 0.78，且上部水体比下部水体偏度值大，冲流上爬速度大；到达岸滩位置整体偏度值有所减小，最大值约为 0.6；在中、高冲泻区偏度值基本小于0，存在部分大于0的情况。工况3中，各断面流速偏度沿垂线分布较为一致，基本呈现从下往上先增大后减小的趋势，溃坝波到达初始岸线前中上部水体的偏度最大值可达到1.5，与工况1和工况2相比偏度值最大；到达岸滩后流速偏度值整体减小，中上部水体流速逐渐趋于正态分布，但依旧具有一定的偏态性。3种工况下，大部分流速偏度分布呈现正偏趋势，流速偏度在中、高冲泻区存在负偏，但负偏值较小且持续时间较短；冲泻区在近底区域每种工况下流速偏度基本位于0附近，表明速度变量接近正态分布，但仍有部分断面的近底流速偏度值偏离0但小于1。这些较小变化说明流速分布具有一定的偏态性，这种现象同孙双科 等[26]运用峰度描述不同水深流速的分布结果相符。在自由表面附近偏度值多大于0，个别断面处的流速偏度小于0，这表明相对于回流方向，冲泻区的上爬流具有较大的速度，冲流以上爬为主。对比3种工况可以看出，缓坡时各断面流速偏度分布规律较为一致，而混合坡度时相差较大。

图7 不同工况下不同断面流速偏度的垂线分布Fig.7 Vertical distribution of velocity skewness in different sections under different cases

2.3.2 流速的不对称度

图8是不同工况下不同断面不同水深处流速的不对称度分布。不同坡度下，上爬流流速的不对称度有所不同：坡度为 1∶10 的岸滩上的流速不对称度的最大值位于近底处，随着从床面到自由水面距离增加而不断减小(图8a)；在坡度为 1∶35～1∶10 的混合坡度岸滩上，流速不对称度最大值出现在断面水深中部，且位于初始岸线附近的流速不对称度值最大，变化最明显(图8b)；由于坡度较缓、水深较大，坡度为 1∶35 的岸滩上的波浪流速不对称度最大值位于断面水深中下部。3种工况下的实验结果表明：随着波浪的传播和波形前倾特性进一步增加，波浪上爬流流速不对称度进一步加强。任意位置处水平不对称度基本都大于0，且从近底层到自由表面，水平不对称度呈现先增大后减小的趋势，这一现象表明在向岸方向波速具有较大的加速度。对比3种工况可以看出，缓坡时各断面流速不对称度分布规律较为一致，而混合坡度时不对称度值相差较大、分布散乱。

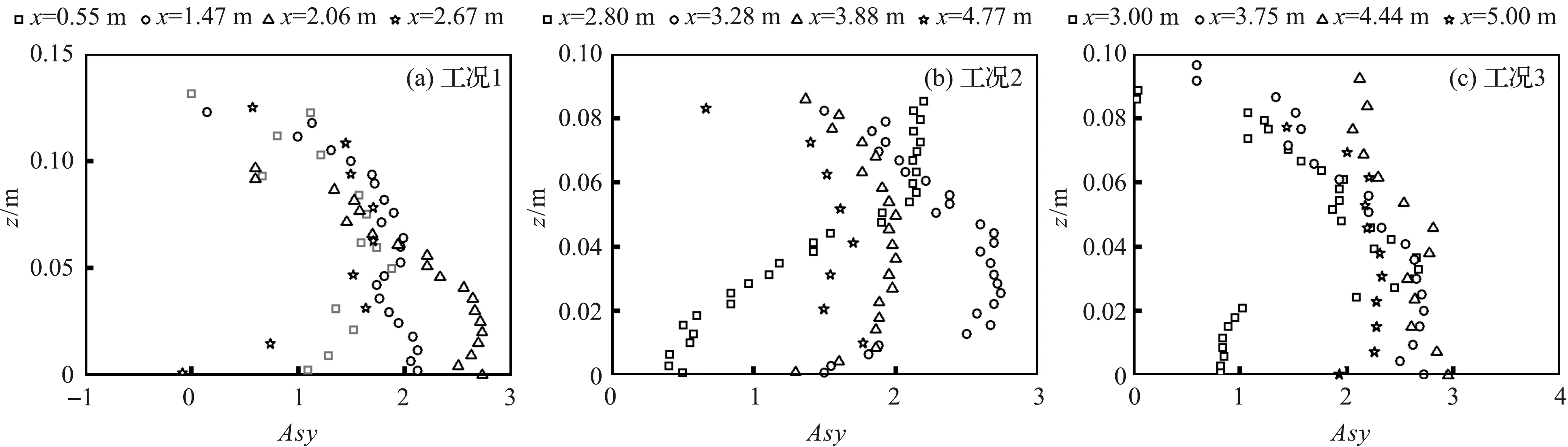
图8 不同工况下不同断面流速不对称度的垂线分布Fig.8 Vertical distribution of velocity asymmetry in different sections under different cases

对流速的偏度和不对称度进行对比分析可知：在工况1和工况2中偏度和不对称度基本呈相反趋势，而在工况3中则有相同的变化趋势。这说明流速的偏度和不对称度存在一定的关系，但在不同位置的流速偏度和不对称度是不同的。对于给定的水深，偏度和不对称度会受到其他因素影响，如本实验结果表明岸滩坡度对其有一定的影响。 RUESSINK et al[27]指出流速偏度和不对称度还强烈依赖于波高和周期等。

3 结论

本文基于不同工况下的物理模型水槽概化实验研究了破碎区至冲泻区波浪沿岸传播过程中非线性特征参数的变化规律。实验结果表明：

(1)波浪的运动形态为波峰高且尖，波谷平且坦，波形沿向岸方向有较大的加速度，上爬趋势明显。波浪沿岸传播过程中波高偏度值基本大于0，呈先减小后增大趋势；波高不对称度均大于0，呈先增大后减小趋势；波高峰度整体呈现先减小后增大的趋势。

(2)破碎区至冲泻区不同断面的流速在向岸方向加速变化明显，大部分流速偏度值大于0，在陡坡涌波到达前的近底层和低冲泻区断面，复合坡的中、高冲泻区断面存在流速偏度值小于0的情况。3种工况下流速表现出不同的非线性分布特征，陡坡和复合坡中，各断面流速偏度分布特征不明显，在缓坡上各断面流速偏度的垂线分布自床面到自由水面呈现先增大后减小的特征。3种工况下流速的不对称度随距床面距离的增大均呈现先增大后减小的变化趋势。

本文通过物理模型实验很好地呈现了冲泻区波浪的非线性特征,但文中仅考虑了单次冲流作用、特定坡度和定床条件，考虑更多形式的波浪作用、岸滩形态的研究有待进一步开展,以便为冲泻区泥沙输运的研究提供理论基础。