基于LS-SVM的多系统融合GNSS-MR潮位反演
2022-04-06游高冲罗孝文尹海博王朝阳
游高冲,郭 杭,罗孝文,尹海博,王朝阳
(1.南昌大学信息工程学院,江西 南昌 330031; 2.自然资源部第二海洋研究所,浙江 杭州 310012)
0 引言
监测海面高度变化对研究全球气候变化、构建海洋高程基准、预防沿海台风等自然灾害具有重要意义。全球导航定位系统多径反射(GNSS Multipath Reflectometry,GNSS-MR)技术是基于全球定位系统多路经效应发展起来的一种新型地基遥感技术,利用地表反射信号与导航卫星直射信号的相干信号获取地表环境信息[1]。相比于全球定位系统干涉(GNSS Reflectometry,GNSS-R)遥感技术[2],GNSS-MR不需要另外架设左旋圆极化天线[3],具有设备要求低、信号源稳定、全天候、覆盖范围广等优势,被广泛应用于地表土壤水分监测[4]、积雪监测[5]和海洋潮汐监测[6-7]等领域中。
LARSONKM et al[8-11]提出基于载波SNR(Signal-to-Noise Ratio)值的GNSS-MR技术,利用该技术对土壤水分和雪深进行了反演研究,并推广到潮位反演。由于GNSS-MR仅使用低高度角信噪比数据,在进行潮位监测时常存在时间分辨率和反演精度低的问题,为此,国内外学者开展了一系列的改进研究。针对GNSS-MR中低阶多项式提取反射信号存在信号混杂的问题,王瑞芳[12]、ZHANG et al[13]等采用经验模态分解提取反射信号的方法,提纯了海面反射信号,提高了潮位反演精度。为提高GNSS-MR潮位监测的时间分辨率,王杰 等[14]采用小波分析的方法,提取反射信号瞬时频率进行潮位反演,有效地增加了潮位反演点数,但该方法提高潮位监测时间分辨率有限,仍难以满足高精度、高时间分辨率潮位监测的要求。陈发德 等[15]利用GPS、BDS、Galileo多系统数据进行融合潮位反演,有效提高了潮位反演的连续性和时间分辨率,但该方法将不同系统的反演结果无差别地组合在一起作为反演结果,联合反演潮位的均方根误差(Root Mean Squared Error,RMSE)为0.323 m,反演精度偏低。何秀凤 等[16]在进行风暴潮反演时,采用滑动窗口最小二乘法,对多系统反演数据进行融合,在提高了风暴潮监测的时间分辨率的同时,也提高了监测的精度,但反演精度仍为分米级。
为进一步提高GNSS-MR潮位反演的时间分辨率和精度,本文提出基于LS-SVM的多系统数据融合潮位反演方法,利用多个系统的潮位反演数据,对LS-SVM进行训练,得到多系统数据融合的LS-SVM潮位反演模型,进而估计出融合后的潮位值,实现高时间分辨率、高精度潮位监测。
1 数据与方法
1.1 GNSS-MR潮位反演方法
图1为利用GNSS-MR技术反演潮位变化的示意图。只考虑1次反射的情况下,载波多路径相位延迟φ可以表示成:
(1)
式中:λ表示载波波长,h表示天线相位中心到海面的高度,θ表示卫星高度角。受多路径效应的影响,海面高度信息以直、反射相干涉的方式保存在混合信号的信噪比中。海面多路径效应下SNR满足如下等式:
(2)
式中:Ad是直射信号幅值,Ar是反射信号幅值,φ是多路径效应相位延迟量。SNR可视为直射信号作用的趋势项与反射信号作用的周期项的叠加,图2给出了GPS 01号卫星的SNR序列和去趋势后的残差序列SNRm。由图2a可知,SNR整体呈抛物线形式,通过二次拟合去趋势,即可得到反射信号作用的周期项(图2b),周期项SNRm满足如下等式:
SNRm=Acos(4πhλ-1sinθ)
(3)
式中:A是信号振幅。记f=2hλ-1,t=sinθ,则上式可进一步整理为如下等式:
SNRm=Acos(2πft)
(4)
周期信号SNRm的频率包含着与潮位反演相关的h值,SNRm是以高度角正弦值为变量的不等间距信号,无法通过傅里叶变换获取。因此,本文采用Lomb-Scargle(L-S)频谱分析[17],提取SNRm的频率f,再由h=f·λ/2、hs=H-h,求出海面高度值hs。图3给出了2020年214年积日部分GPS卫星反射信号SNRm及相应的L-S频谱图,L-S频谱图(图3b)中曲线峰值所对应的横坐标为有效反射高h。

图1 GNSS-MR监测潮位变化示意图
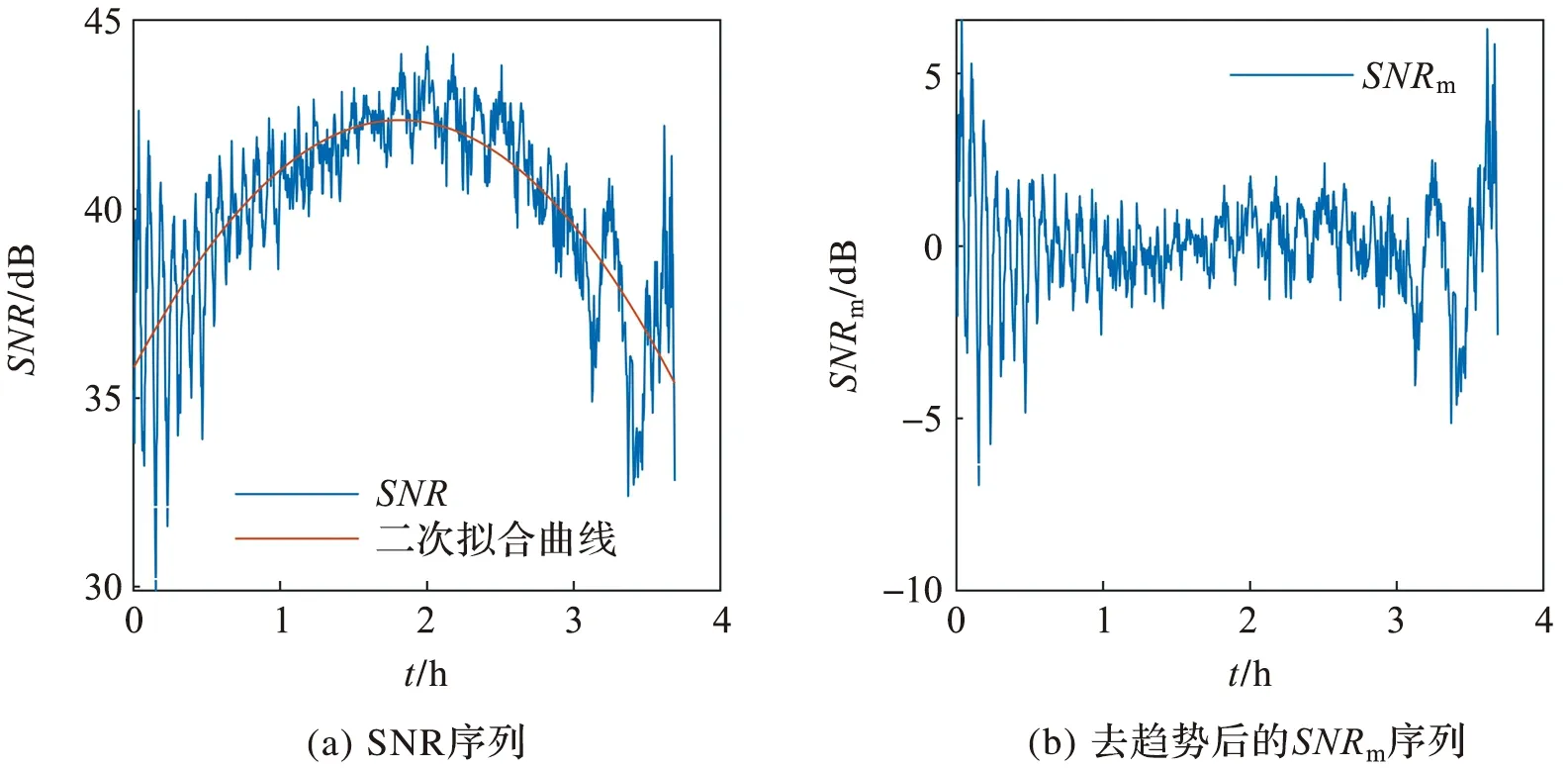
图2 GPS 01号卫星SNR序列(a)和二次拟合去趋势后的残差SNRm序列(b)Fig.2 SNR sequence diagram (a) and residual SNRm sequence chart after two fitting detrended trend (b) of GPS 01 satellite

图3 HKQT站GPS部分卫星海面反射信号SNRm(a)和相应的Lomb-Scargle频谱(b)Fig.3 Partial satellite sea surface reflection signal SNRm (a) and corresponding Lomb-Scargle spectrum (b) of GPS at HKQT station
1.2 LS-SVM多系统数据融合方法
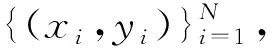
根据SVM思想,在高维空间的回归方程为
f(X)=〈ω,φ(x)〉+b
(5)
式中:〈·,·〉表示点积;ω∈Rnk,是原权重空间中的权重向量;φ(·):Rn→Rnk,是将输入数据映射到高维特征空间的非线性函数;b是偏置量,b∈R。
对于LS-SVM可将优化问题转化为[18]
(6)
式中:ek为样本误差;γ表示正则化参数,在噪声较小的情况下,较小的γ可以避免过度拟合。此时的约束条件为
yk=〈ω,φ(xk)〉+b+ek,k=1,…,N
(7)
拉格朗日函数为
(8)
式中:αk为拉格朗日乘子,αk∈R。根据KKT条件消去ω和ek,得到如下线性方程式:
(9)
式中:y=[y1,y2…,yN]T;1v=[1,1,…,1]T;α=[α1,α2,…,αN]T;Ωk,l=〈φ(xk),φ(xl)〉=K(xk,xl),k,l=1,…,N。
利用最小二乘法对公式进行求解,即可得到LS-SVM 非线性回归模型:
(10)
基于LS-SVM多系统数据融合方法的潮位反演性能与核函数K、核参数σ和正则化参数γ的选取密切相关[18],本文选用能很好反映模型复杂程度和普适性较好的径向基函数为核函数,通过网格搜索法优选σ和γ参数。基于LS-SVM的多系统融合模型潮位反演流程如图4所示。

图4 基于LS-SVM的多系统融合潮位反演流程图Fig.4 Flow chart of multi system fusion tidal level inversion based on LS-SVM
1.3 实验数据及处理
为验证基于LS-SVM的多系统融合潮位监测方法,本文选取2020年香港北岸HKQT站(22.29103351°N,114.21322098°E)214至244年积日的卫星观测数据进行潮位反演实验。该测站配备有TrimbleNETR9型号接收机,可以接收GPS、BDS、Galileo、GLONASS四个系统的卫星信号。此外,该站同一位置建设有验潮站,提供1次/6 min的潮位数据,可以用于对LS-SVM多系统融合潮位监测方法的精度进行评估。
潮位数据由国际海平面实施网( http://www.ioc-sealevelmonitoring.org/)提供,该潮位数据以平均海平面(Mean Sea Level, MSL)为基准。为使反演潮位值与验潮站的潮位数据具有统一的基准,本文依据该网站提供的验潮站修订本地参考图(Revised Local Reference, RLR)进行相应的高程转换,可得到HKQT站天线相位中心到MSL的高。图5中RLR的椭球高为-8.274±0.004 m,经精密单点定位解算出天线相位中心的椭球高为5.683 m,将天线椭球高减去RLR椭球高,再减去7.01 m即可得到天线相位中心到MSL的高度值,经解算高度值为6.407 m。
潮位反演所需的载波波长、高度角、方向角、天线高等基本参数设定如表1所示。

图5 验潮站修订本地参考图Fig.5 Revising local reference diagram of tide gauge station

表1 GNSS-MR潮位反演参数表Tab.1 Inversion parameters for GNSS-MR tide level
2 结果与讨论
2.1 单系统潮位反演结果分析
利用香港HKQT站提供的2020年214年积日至2020年244年积日连续30 d的GPS、BDS、Galileo、GLONASS卫星数据对HKQT站附近潮位进行反演,结果如图6所示。图6a、6c、6e和6g分别为GPS、BDS、Galileo和GLONASS反演结果及验潮站实测的潮位变化曲线,从中可以看出,HKQT站附近潮位在 ±1 m 区间范围内周期性波动,各系统反演点均落在曲线上或曲线附近,反演点的变化趋势同验潮站实测潮位变化趋势相同,反演潮位值和实测值具有明显的一致性,表明4个系统均能有效实现潮位监测。将反演潮位值减去同时刻验潮站实测潮位值,即可得到反演潮位的偏差值,图6b、6d、6f和6h分别GPS、BDS、Galileo和GLONASS系统反演潮位的偏差序列,各系统反演偏差均在±0.5 m范围内变化。本文采用均方根误差、相关系数和时间分辨率作为潮位反演的性能评定指标,评定结果如表2所示。

表2 单系统潮位反演性能对比Tab.2 Comparison of inversion performance of single systems tidal level
由表2可知,4个系统均能用于HKQT站附近的潮位监测,且各系统反演潮位的精度相当,反演精度在0.120~0.139 m之间,相关性系数在0.953 6~0.963 2 之间,反演潮位值同验潮站实测值之间具有极强的相关性。各系统反演潮位的时间分辨率差异较大,其中GLONASS系统潮位监测时间分辨率最高,平均1.23 h一个反演值;BDS系统潮位监测时间分辨率最低,平均5.56 h一个反演值。总体而言,单系统GNSS-MR潮位反演精度和时间分辨率均较差,难以满足高精度、高时间分辨率潮位反演性能需求。
2.2 LS-SVM融合潮位反演结果分析
为提高潮位监测的时间分辨率和精度,考虑到不同系统之间的互补性,本文采用LS-SVM对GPS、BDS、Galileo、GLONASS反演潮位数据进行融合。首先,将4个系统的反演潮位值组合在一起,作为 LS-SVM 的训练集;然后对训练集进行LS-SVM训练,并采用十倍交叉验证方法分析确定正则优化参数γ和核参数σ,得到潮位LS-SVM模型;最后,由LS-SVM潮位反演模型估计出潮位值。
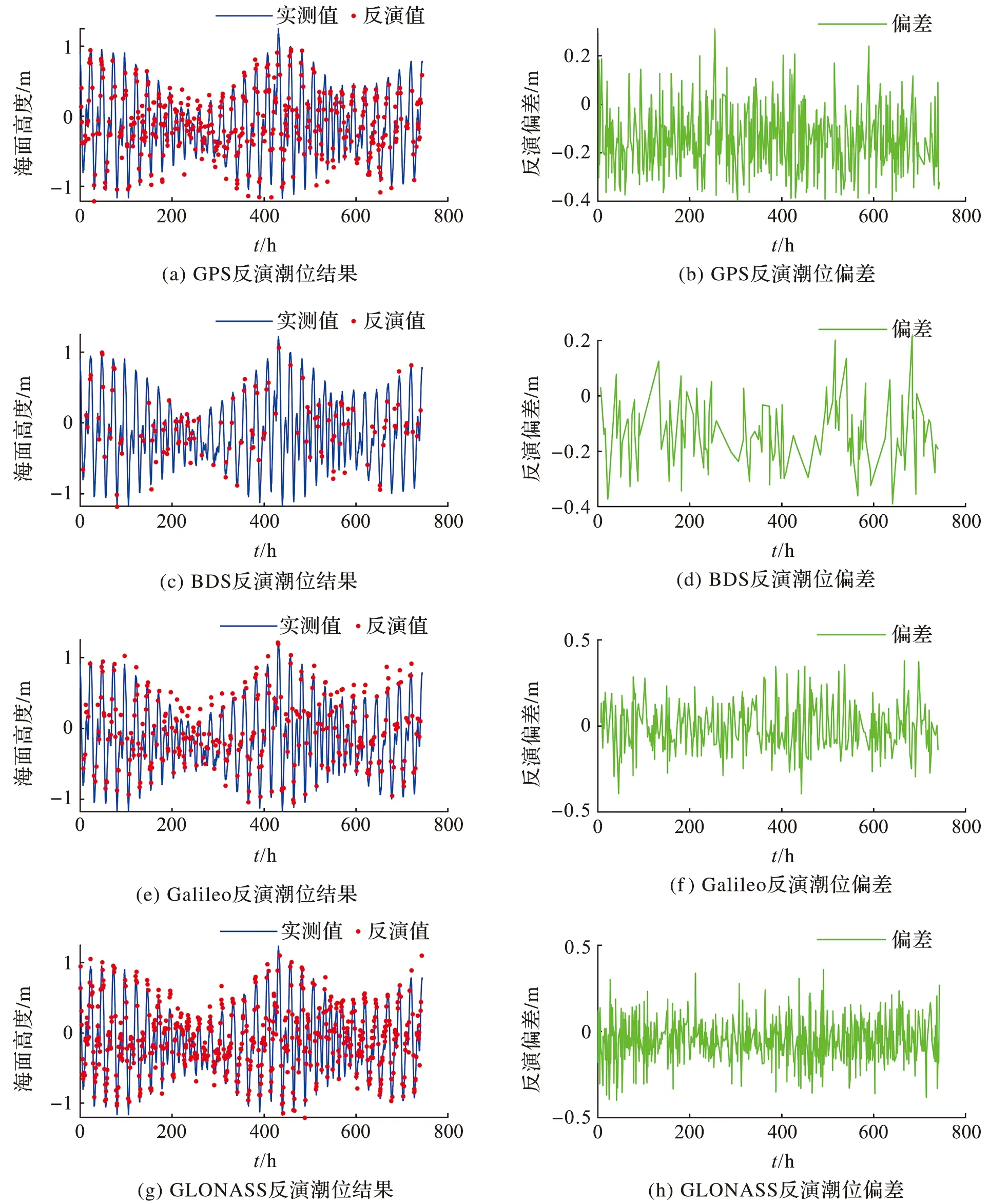
图6 GPS、BDS、Galileo、GLONASS反演潮位结果、反演偏差及验潮站实测潮位曲线Fig.6 GPS, BDS, Galileo and GLONASS respectively inversion tidal level results, inversion deviations and measuring tide level curves at tide gauge station
图7a是GPS、BDS、Galileo、GLONASS反演结果组合得到的训练集序列,4个系统组合后反演点数目明显增多,反演点数目达到1 487个,平均每0.5 h一个反演值,相比于GLONASS系统,时间分辨率提高了59.3%以上,极大地增强了GNSS-MR潮位监测的时间分辨率。图7b是与训练集相对应的反演偏差序列,反演偏差在±0.5 m区间内变化,训练集的RMSE值为0.140 m,由此可见,直接将不同系统反演结果叠加在一起,并不能提高潮位反演精度。图7c 是训练集经LS-SVM训练后得到的LS-SVM潮位反演模型估计的潮位时间序列。由图7d可知,LS-SVM潮位模型估计值的偏差幅值多集中在-0.2~0.2 m区间内,较训练集偏差明显减小。经分析,LS-SVM潮位反演模型估计潮位值的RMSE值为 0.053 m,较训练集RMSE值减小了62.1%,较单系统潮位反演RMSE最小的BDS系统,RMSE值减小了55.8%,较单系统潮位反演时间分辨率最高的GLONASS系统,时间分辨率提高了59.3%。由此可见,LS-SVM融合模型在提高潮位反演时间分辨率的同时,也提高了潮位反演精度。
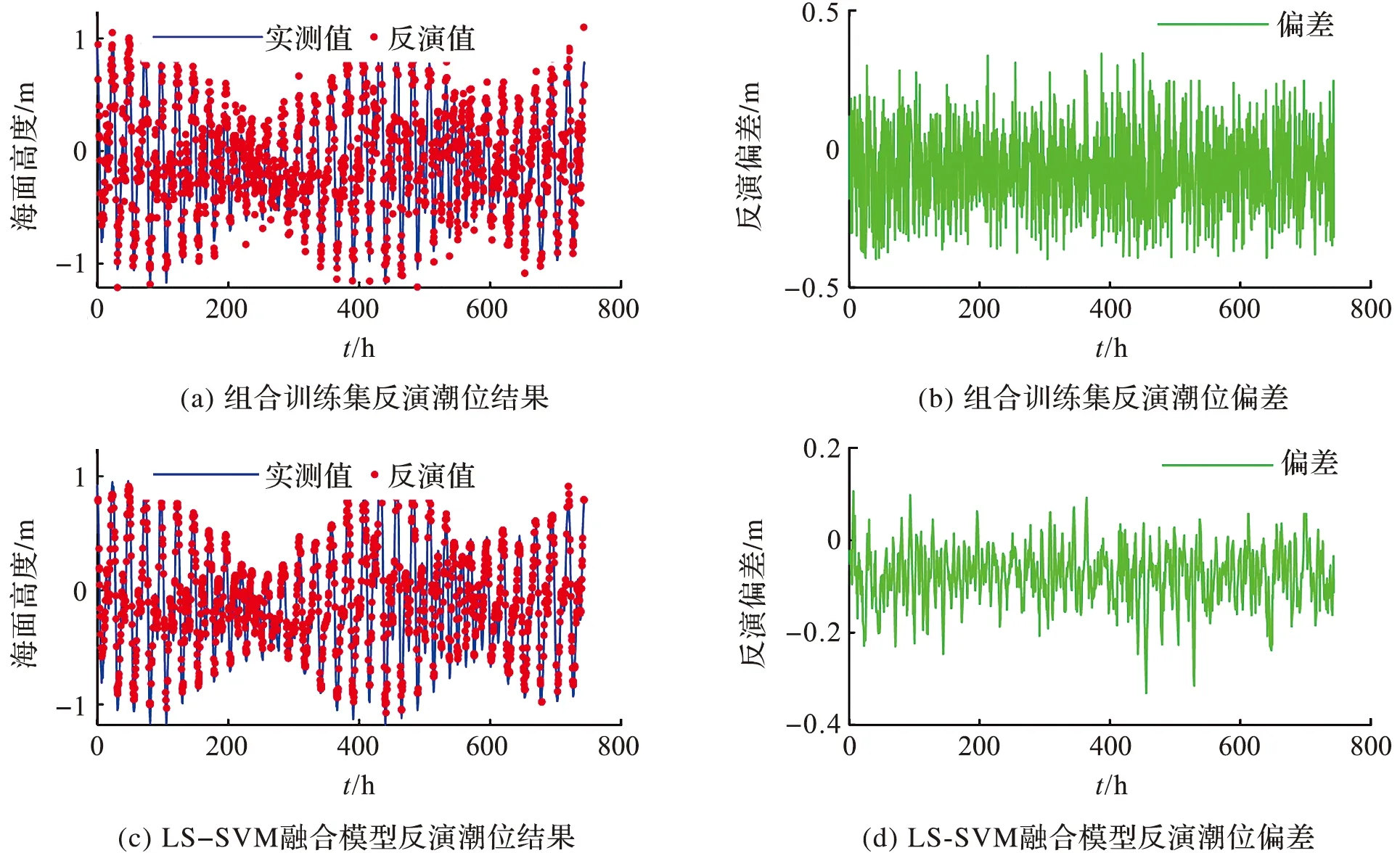
图7 4种系统组合的训练集和经LS-SVM融合后的潮位反演结果及相应的反演偏差序列Fig.7 The training set of the four system combination and the inversion result of tidal level after LS-SVM fusion and the corresponding inversion deviation sequence
图8是LS-SVM融合模型反演潮位值与实测潮位值的相关性散点图,经LS-SVM融合后,反演潮位值与实测潮位值更紧密地分布在直线附近,反演潮位值与实测值的相关系数为0.992 5,较训练集提高了4.2%;较单系统潮位反演相关性系数最大的GLONASS系统,相关性系数提高了3.0%,有效提高了潮位监测的精度。

图8 LS-SVM多系统融合反演潮位值与验潮站实测潮位值相关性图Fig.8 Correlation diagram of LS-SVM multi system fusion inversion of tidal level and measured tidal level at tide gauge station
2.3 多种潮位融合算法反演结果对比分析
为了分析LS-SVM潮位融合算法的性能,本节将对比LS-SVM、SVR、滑动窗口最小二乘法3种潮位融合算法。基于SVR的多系统融合方法同LS-SVM方法类似,对多系统组合训练集进行SVR训练,得到潮位反演模型,进而估计出潮位值。本文在利用SVR进行多系统数据融合时,选用高斯径向核函数RBF和网格寻优法进行参数优选,不敏感损失系数ε设定为0.1,SVR算法详见文献[19]。
图9a和9b分别为基于SVR的数据融合潮位反演结果图和反演偏差图。经SVR融合后,反演潮位的RMSE值为0.111 m,较训练集RMSE值减小了20.7%;较BDS潮位反演RMSE值减小了7.5%,反演精度有所提高。图9c和9d分别为基于滑动窗口最小二乘法的多系统融合潮位反演结果和偏差图,同训练集相比,偏差变化幅值明显减小。经滑动窗口最小二乘法融合后,RMSE值为0.090 m,较训练集RMSE减小了35.7%,较BDS系统RMSE值减小了25%。图10为基于SVR算法和滑动窗口最小二乘法的多系统融合潮位反演结果与验潮站实测值的相关性图,经分析,SVR反演结果与验潮站实测值之间的相关系数为0.971 1,较训练集相关性系数提高了2.0%;滑动窗口最小二乘法反演结果与验潮站实测值的相关系数为0.980 4,较训练集提高了2.9%。由此可知,这两种方法均能提高潮位反演精度。此外,基于滑动窗口最小二乘法的多系统融合潮位反演方法的反演精度为厘米级,优于基于SVR的多系统融合潮位反演方法。

图9 基于SVR算法和滑动窗口最小二乘法的多系统数据融合潮位反演结果及偏差Fig.9 The inversion result and deviation of multi system data fusion tide level based on SVR algorithm and sliding window least square method
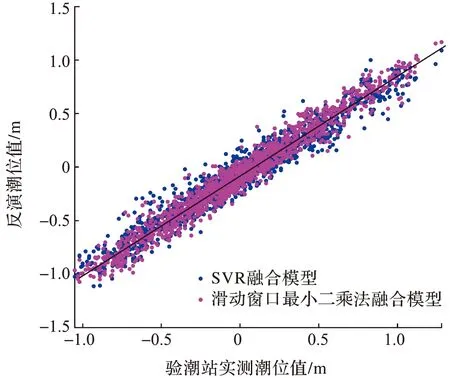
图10 基于SVR算法和滑动窗口最小二乘法反演潮位与实测潮位的相关性图Fig.10 Correlation diagram between the inversion tide level based on the SVR algorithm and the sliding window least square method and the measured tide level
由表3可知,3种多系统融合模型均能提高GNSS-MR反演潮位的精度和时间分辨率,且时间分辨率相同,均为0.5 h。LS-SVM模型较SVR模型,RMSE值减小了52.3%,相关系数提高2.2%;较滑动窗口最小二乘法,RMSE值减小了41.1%,相关系数提高了1.2%。LS-SVM融合模型优于SVR融合模型和滑动窗口最小二乘法融合模型。

表3 3种融合模型潮位反演性能对比Tab.3 Comparison of inversion performance of three kinds of fusion models
3 结论
本文针对单系统GNSS-MR潮位监测中时间分辨率和反演精度低的问题,提出一种基于LS-SVM的多系统融合潮位反演方法,利用香港HKQT站提供的卫星观测数据,对比了滑动窗口最小二乘法、SVR算法和LS-SVM算法在多系统融合潮位反演中的表现,结果表明:
(1)单系统GNSS-MR潮位反演的RMSE最小值为0.120 m、最大值为0.139 m;相关系数最大值为 0.963 2,最小值为0.953 6;GLONASS潮位反演的时间分辨率最高,BDS潮位反演的时间分辨率最低。单系统潮位监测的时间分辨率和反演精度偏差无法满足高精度、高时间分辨率潮位监测的要求。
(2)在多系统融合GNSS-MR潮位反演方面,基于LS-SVM的多系统融合潮位反演比滑动窗口最小二乘法、SVR算法具有更优的潮位反演性能。相比于SVR模型,LS-SVM模型的RMSE值减小了52.3%,相关系数提高了2.2%;相比于滑动窗口最小二乘法,LS-SVM模型的RMSE值减小了41.1%,相关系数提高了1.2%。
本文所用方法较单系统而言,时间分辨率提升到0.5 h,为进一步提高时间分辨率,在未来可以采用小波变换、NTFT等视频变换方法,提取瞬时反射信号的频率值,达到提升时间分辨率的效果。
