基于ARIMA 和LSTM 的城市轨道交通客流量预测

潘念然

(上海体育学院经济与管理学院，上海 200000)

地铁作为满足大众基本出行需求的一个重要方式，具有故障率低、运力大、稳定安全等优点。同时，建立较为完善的地下轨道交通网络，既可以改善地面公共交通能力不足的不利局面，又可以促进城市基础设施建设，拉动经济社会发展。在城市轨道交通发展建设和运营中，客流预测一直是相关研究和实践的一个重要内容。特别在当前城市轨道交通运力快速增长和客流需求变化较快的情况下，客流预测研究的重要性和必要性更加凸显。在城市轨道交通客流预测方法上，已经涌现出了多种模型，其中，单变量自回归移动平均模型(ARMA)是最为常用的传统预测方法。ARMA 考虑了差分影响，是自回归(AR)和移动平均(MA)模型的结合，被广泛应用于基于时间序列的预测研究中[3-4]。近年来，随着人工智能的发展，基于深度学习算法的支持向量机(SVM)、随机森林(RF)、递归神经网络(RNN)、长短期记忆(LSTM)等正成为预测研究的重要方向。其中，LSTM能够识别数据的结构和模式，能够挖掘数据中蕴含的非线性和复杂性，被广泛用于基于时间序列的预测研究[7-10]。目前，在城市轨道交通客流预测研究中，综合应用传统ARMA 模型和当前处于前沿的LSTM模型的研究仍较少。基于此，本文综合应用ARMA 和LSTM两种方法展开城市轨道交通客流预测研究，通过对比分析来确定哪个模型具有更好的准确性和精度，由此为相关理论研究和实践应用提供参考和借鉴。

1 研究方法

1.1 模型选择

作为传统预测模型的代表，ARIMA 模型能够处理数据的非平稳性，而作为基于深度学习算法的代表，LSTM方法能够对非线性时间序列数据进行建模。研究应用城市轨道交通客流的时间序列数据，分别构建ARIMA 和LSTM 模型来预测城市轨道交通客流量，并通过比较预测结果的均方根误差来评估两个模型的预测精度和性能。

1.2 ARIMA 模型

自回归滑动平均模型：

如果序列Xt不仅与过去的状态有关，而且对之前进入系统的外部冲击也有一定的依赖性。当这种动态特征用一个既包含滞后项又包含过去外部冲击的模型来描述时，通常称为自回归移动平均模型，其一般结构为：

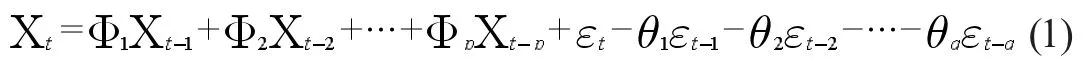
根据时间序列是否具有季节性变化，其结构可分为ARIMA(p,d,q)和ARIMA(p,d,q)×(P,D,Q)S，其中p 和q 是自回归的阶数和移动平均阶数，d 和D 是非季节性和季节性差异时间，P 和Q 是季节性自回归阶数和移动平均阶数，S 是时间序列周期或周期长度。

ARIMA(p,d,q)×(P,D,Q)S

对于周期为S 的乘积季节模型，该模型一般定义为:

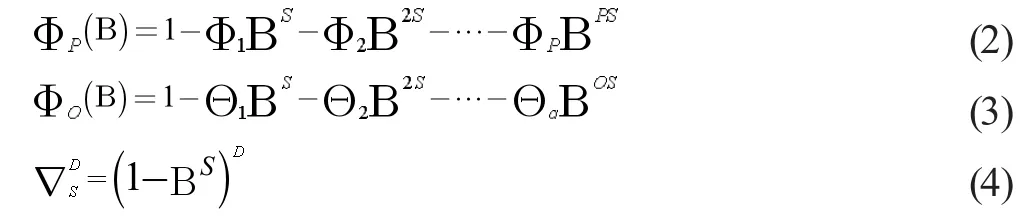
其中，上式(2)是以S 为周期的时间序列的P 阶自回归运算符，上式(3)是以S 为周期的时间序列的Q 阶移动平均运算符，上式(4)是以S 为周期的时间序列的D 阶季节性差分算子。

1.3 LSTM 模型

LSTM 是一种改进的RNN 算法，主要用于时间序列预测。LSTM给RNN 增加了三层，分别是遗忘门、输入门和输出门。遗忘门以一定的概率决定是否忽略前一层的隐藏单元状态；输入门确定输入以更新序列位置；输出门决定了最后时刻的隐含规则和当前时刻的联合状态。

2 案例研究

2.1 数据采集

城市轨道交通的线路固定，受外界因素的干扰较小，居民使用轨道交通的时间周期性很强，所以整体的城市轨道交通客流量数据带有时序性特点，即客流量会随着时间点、季节、月份的变化而变化，但是最基本的是以周为单位的变化周期。本文采集的数据具体时间区间为2019 年4 月1 日至2019 年6 月13 日。在时间序列数据分析中，不同的时间区间会有不同的变化。因此，在此基础上，本文将数据分成日客流量数据和分时客流量数据,然后将日客流量和分时客流量分别进行模型拟合，分析精度。

2.2 数据分析

2.2.1 平稳性检验

日客流量数据具有季节性特点，为了减少误差，对原始序列进行季节性差分，时间序列通过ADF 检验，P 值为0.000＜0.05。分时客流数据是非平稳的，为了减少误差，对原始序列进行一阶差分，时间序列进行ADF 检验，P 值为0.000＜0.05。在三个显著水平上，季节差分序列和一阶差分序列都是平稳的。

2.2.2 确认ARIMA 模型参数

本文首先建立了ARIMA 模型，并对参数进行了估计。为了使建模更加严格，我们使用AIC 和BIC 准则来确定模型的参数。对于日客流量，最小的AIC=1041.298，对应的模型是ARIMA(3,0,1)(0,1,1)，对于分时客流量，最小的BIC=71779.19，对应的模型是ARIMA(7,1,7)。

2.2.3 ARIMA 模型预测

从图1 可以看出，日客流预测结果的残差序列是独立的白噪声序列，说明该模型拟合数据。图2 显示了分时客流的残差序列QQ 图。如图1 和图2 所示。

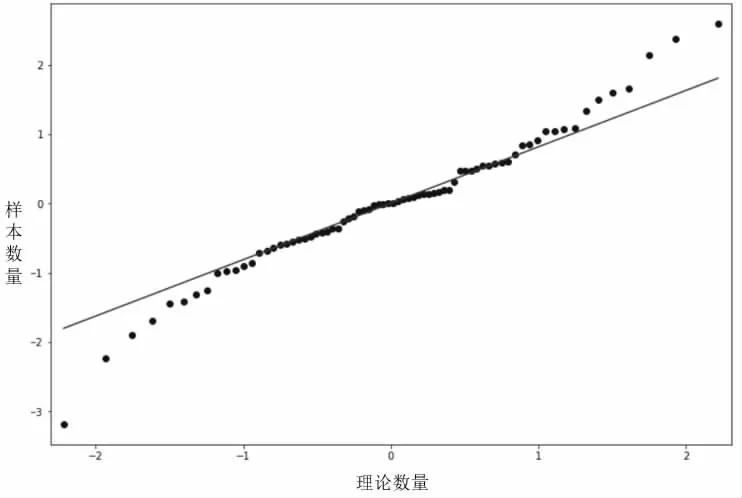
图1 日客流量残差序列QQ 图

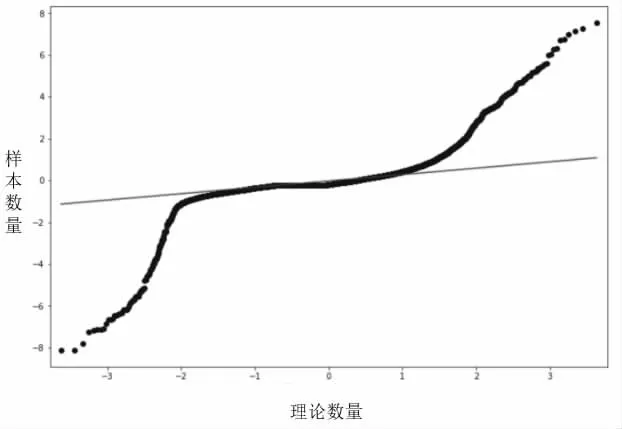
图2 分时客流量残差序列QQ 图

根据上述可得拟合模型ARIMA(3,0,1) (0,1,1)和ARIMA(7,1,7)。通过编程得到的结果如下：日客流量ARIMA 模型预测结果RMSE=3167.53，分时客流ARIMA 模型预测结果RMSE=126.34。结果表明，当预测数据具有季节性特征时，误差约为3,167.53，当预测数据具有非平稳性时，误差约为126.34。预测结果如图3 和图4 所示。

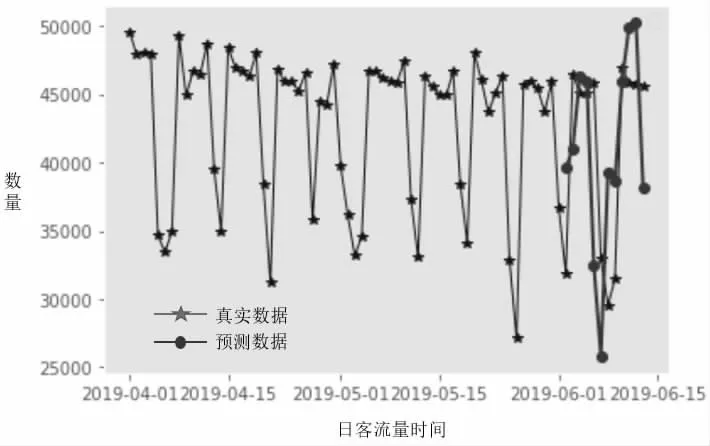
图3 日客流量ARIMA 模型预测

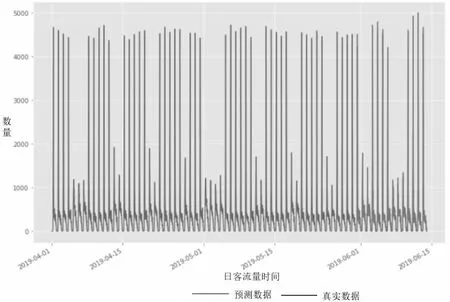
图4 分时客流量ARIMA 模型预测

2.2.4 确认LSTM 模型参数

神经网络中最关键的是确定输入神经元的数量、隐藏层的数量和隐藏单元的数量。隐藏层和受保护组过多会导致网络学习速度延长，太少将缺乏必要的学习能力。本文的日客流量和分时客流量设定的输出和输入均为一维特征，可以看出训练效果较好，如图5 和图6 所示。

图5 日客流量LSTM 模型损失

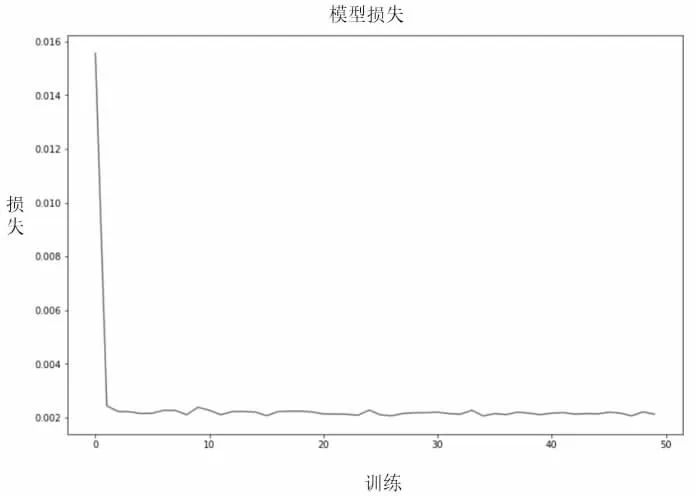
图6 分时客流量LSTM 模型损失

2.2.5 LSTM 模型预测

使用训练好的LSTM模型预测数据，结果如图7 和8 所示。

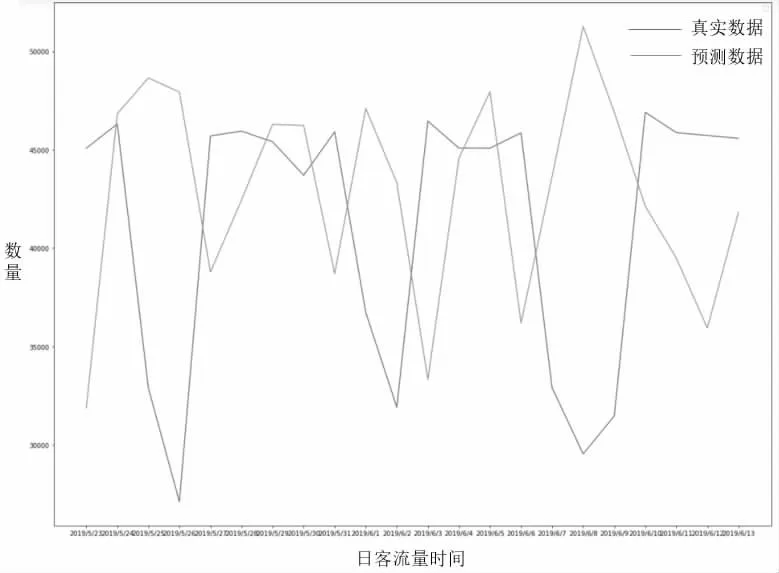
图7 日客流量LSTM 模型预测

日客流量LSTM模型的预测结果为RMSE=41200.85，这意味着对于具有季节性特征的数据，每个LSTM预测的均方根误差约为41200.85。LSTM 模型的分时客流预测结果为RMSE=211.52，这意味着对于不平稳的数据，每个LSTM预测的均方根误差约为211.52。

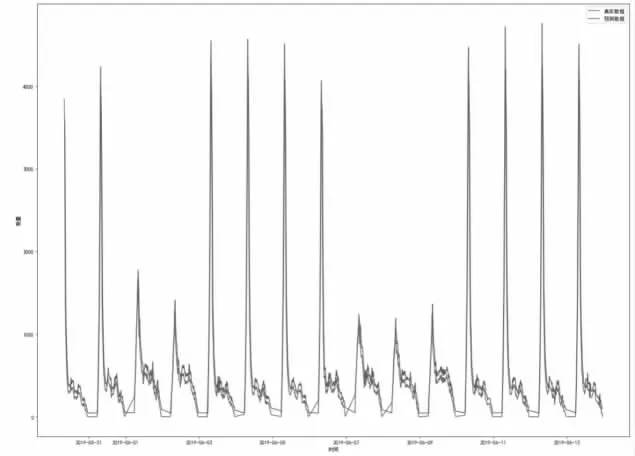
图8 分时客流量LSTM 模型预测

2.3 结果分析

平均绝对误差用于衡量总误差的平均值，均方根误差用于衡量误差的平均大小，两者都可用来评价模型的拟合精度。为了更加直观地分析两种模型的预测结果，本文使用RMSE 来评估模型。

不同预测数据和方法的准确率结果如表1 所示。均方根误差结果因数据量、预测方法和时间间隔而异，RMSE 越小，模型的精度就越高。在时间粒度上，对于日客流数据，ARIMA方法的均方根误差小于LSTM方法，预测效果更好；对于分时客流，LSTM 方法的均方根误差大于ARIMA 方法，从RMSE 结果来看，ARIMA 的预测优于LSTM。

表1 不同频率数据的均方根误差

3 结论

本文在对城市轨道交通客流预测模型进行系统分析的基础上，分别应用ARIMA 模型和LSTM模型对城市轨道客流进行拟合和预测，进而对两个模型预测的结果进行对比分析，从而评估模型预测的精度和性能。研究结果表明，首先，对于日客流，ARIMA 优于LSTM，这是因为日客流量的数据不足，而LSTM的网络需要大量的数据来训练以此来达到更精确的结果；对于分时客流量，将两种方法结合起来效果更好。其次，预测的质量与数据质量和模型选择有关，但输入数据的清洗和选择也很关键。在满足模型性能要求的前提下(例如，某些模型需要非常大的数据集)，同一数据集可以使用不同的模型。为此，更重要的是对输入数据进行分析，挖掘数据的深层次关系，即优化输入数据集。对于本文中的数据，日客流量的预测最好用ARIMA 算法来预测；对于分时客流的预测，LSTM 神经网络也可以作为ARIMA 的替代方法用于预测，预测值与数据整体趋势大致相同，峰值存在误差，但整体偏差不大，结果表明需要优化或组合方法来提高较短时间间隔预测的准确性。