“双减”背景下初中数学学科育人的“三阶”实践路径—— 以“丰富的图形世界”数学实验教学为例

孙朝仁， 朱桂凤

(1.苏州市教育科学研究院， 江苏 苏州 215004；2.连云港市凤凰学校， 江苏 连云港 222003)

针对义务教育阶段课业负担太重这一突出问题，中共中央办公厅、国务院办公厅印发了《关于进一步减轻义务教育阶段学生作业负担和校外培训负担的意见》(以下简称《“双减”意见》)。《“双减”意见》指出，“要提升课堂教学质量，教育部门要指导学校健全教学管理规程，优化教学方式，强化教学管理，提升学生在校学习效率”。要减轻学生负担，根本之策在于全面提高学校教学质量，做到应教尽教，强化学校教育的主阵地，使学生回归校园、回归课堂。换言之，“双减”的背后意蕴是“提质增效”，需要走出一条学科育人的有效路径。

本文以《丰富的图形世界》(苏科版《数学》七年级上册)一课的教学实践为例，以数学实验活动为载体，阐述如何用“双减”的视野教知识、用“双减”的思想教方法、用“双减”的教学行为教人成长，以此构建初中数学学科育人的“三阶”实践路径。

一、第一阶：双情境抽象，通过思维减负揭示数学世界与外部世界的一致性

抽象是数学的三大能力之一，是从数学现象中揭示出数学本质的唯一路径。双情境抽象包括数学内部关系的抽象和数学外部关系的抽象。其中，数学外部关系抽象旨在建立数学与生活关系的抽象，是用数学的思维方式刻画现实世界的一种模型意识。比如，在数学世界里，为了研究点、线、面的需要，我们往往会把一个广场或交叉路口抽象为一个点，甚至把一块陆地抽象为一个点，而把笔直宽广的城市大道抽象为一条直线，把平静的湖面、水面抽象为一个平面等，这样用数学的眼光观察、刻画、表征生活世界的表象行为，就是常见的外部数学关系抽象。内部关系抽象指向数学到数学关系的抽象，是建立数学知识关系的一种结构化行为，是学生“会一题、通一类、连一片”绕不开的路径。比如，选择恰当的分类标准对常见的几何体进行分类就是数学内部关系抽象的一种具体表现。再如，用两块全等的直角三角板拼图，这一分类拼图(分别用长直角边、短直角边、斜边叠合)的过程也是对数学内部关系的二次抽象；将正方体的展开图归纳为“一四一型(9种)、二三一型(3种)、三三型(1种)、二二二型(1种)”，也是数学内部关系的二次抽象。这种揭示数学内部关系或数学变化规律的过程，也是初中阶段数学内部关系抽象的常见思维方式。

其中，“思维减负”表现在“大思考、小动笔”，表现在“学体验、学思考、学表达”，还表现在横向水平抽象、纵向水平抽象的过程中学生的思维互动、思考交往、问题质疑以及清晰地表达数学认识等“学数学”的过程。数学家在创造数学的过程中相互之间的合作交流极大地有利于其数学创造[1]。在“双减”政策的背景下，减轻过重课业负担是一种辩证法、是一种认知哲学，不止于布置恰当、有效、适量的作业，更在于提高数学课堂学习实效，驱动“想学好”数学的心理状态。这样，力图让学生在获得知识、获得方法的同时，获得人的全面发展与成长，才是数学课堂减负的本质。减负的背后意蕴就是增值，思维减负能使得“冰冷的数学思考”转化为暗流涌动的“火热思维”，能使得学生建立一种稳定的学好数学的情怀。因此，减负是数学育人的有效路径，是学生自然生长的法定标准。

当代认知心理学认为，学习是一种迁移。双情境抽象起于思维减负，成于数学世界与外部世界的一致性，终于知识迁移和学生的适性成长。当一门学科远离它的经验本源继续发展的时候，或者远离社会向前迈进都是不利于学生的思维成长的。这就是通过数学“双”情境抽象、或者通过二级抽象获得研究对象的根本原因，也是推动数学社会学发展的一个视角。其实，20世纪90年代以来，“数学社会学成为数学教育和数学哲学话题的核心成分”是必然产物。为此，在双情境抽象的过程中，需要注意以下几个方面的思考：一是，外部抽象，让学生产生思维的迫切性；二是，内部抽象，让学生知觉到学的必要性和价值；三是，纵向同化，用数学的思维表征数学世界，丰富原有认知结构的意义属性，突出概念“可接受”的心理状态。这样复合抽象，能使得概念连同它的语义、图式命题存储于长时记忆系统，并可双向调用，具有高度的内部关系一致性。

比如，在学习“丰富的图形世界”这一内容时，执教者就是遵从双情境抽象宗旨，让学生在思维减负的课堂学习过程中，不经意地建立了数学外部关系与内部关系的一致性。或许，在单一数学知识范畴，师生并不觉知“我们在成长”，因为少做了一些题，多了一些思考。但从学习心理学看，类似于图1的设计指向，却客观地反映了执教者对数学育人的一种努力和追求。

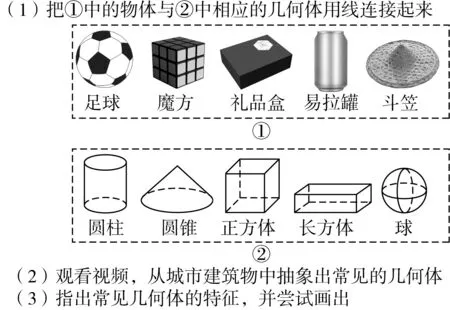
图1 双情境抽象

从设计宗旨看，图1设置的目的是力图让学生通过二次抽象，建立研究对象的表象，知道概念是什么、为什么和怎么样，进而在建立概念表象的基础上，体验数学世界与外部世界的一致性，促进原型定向目标过程的实现，发展学生的模型意识；从教体验的角度看，在图1中，通过“连线”的直观方式，激活学生的已有经验，建立新旧知识衔接的思维节点，体验横向数学化特征；从教思考的角度看，一方面让学生从众多的城市建筑物中抽象出常见的几何体，这本身就是一种表象思考，是原型定向必经之途；同时，在二次抽象的过程中指出常见几何体的特征，重视“点无大小、线无粗细、面无厚薄”基本特征，并通过“画出”的方式，将感性认识转化为理性思考，这就是数学世界纵向同化的一种思维方式。

简而言之，一般来说，获得研究对象的过程往往需要二级抽象(生活→数学、数学→数学)和二次抽象(数学对象及其数学对象特征的揭示)过程，方能建立纵向同化数学知识目标，体验“用数学的思维思考现实世界”的育人目标。其中，图1中的问题(1)(2)属于双情境抽象，反应外部世界与内部世界关系一致性，问题(3)属于纵向同化的思维方式，是知识迁移的心理前提，标志着原型定向法定标准的建立，是获得研究对象心象的一种表现。同时，在这里需要指出，减负思维就是减轻认知压力，缓解数学认知的畏难情绪，解除新旧知识融通的心理障碍，进而铺设学生学得好数学的心理基础。

二、第二阶：三分类建模，通过基数减负建立数学世界内部的贯通性

数学建模是对数学模型的一种组织和优化，是触类旁通的思维基础和心理支架。三分类建模就是选择恰当的分类标准对一类思维对象的不同侧面进行二次、三次研究，力图揭示概念的“同与异”的一种辩证特征，带有一定层面的数学“相对论”色彩。比如，对常见几何体的分类可以从“有、无曲面”的视角进行分类，也可以从“有、无顶点”的视角进行分类，还可以从“柱体、锥体、球体”的角度进行分类，这样从多个侧面揭示一类事物的数学特征的研究方法，是建立数学世界内部知识贯通性的基本方法。这种多视角的研究“同一问题”的基本方法，就是三分类建模的一个具体例子。

从分类建模的视角看，数学学科内容划分为“数与代数、图形与几何、概率与统计、综合与实践”四个领域，这就是一阶分类；在“数与代数”领域的经典数学模型包括代数模型、方程模型、不等式模型、函数模型等模型思想，这就是二阶分类；在函数家族中包括一次函数模型、反比例函数模型、二次函数模型、指数函数模型、对数函数模型、三角函数模型、反三角函数模型等类别，这就属于三阶分类。因此，三分类建模的本质是系统化、结构化、模式化、支架、图式等教学行为和教学行为系统。

《义务教育数学课程标准(2011年版)》明确指出，要站在整体的高度、系统的高度学习相关知识，对于某些问题可以从不同侧面进行研究、从不同角度进行分析、从不同层次进行理解，进而提高思维载体的育人价值。这就是“类”的教育思想。比如，“三视图”问题(主视图、左视图和俯视图)，可以放在小学阶段研究，也可以放在初中阶段研究，还可以放在高中阶段研究，当然甚至可以放在大学阶段研究，关键是学生需要什么和“可接受”的心理水平系数？这些“类”的行为要素及其子要素，需要重组、需要关注、需要深入思考。也就是说，任何一个数学教师在教学之前一定要充分思考学生需要什么，然后根据学生的需要，在学生可接受的思维范畴，让学生获得“可能”的发展，并驱动学生的成长，这本身就是基数减负(整合、重组意味着重质轻量)。

当然，从数学教育过程看，基数减负由来已久，并不是新名词，而是随数学教育的发展不断地更新。教学改革需要同时关注作为显性表现的教学行为及其背后隐性的教学观念[2]，数学教育是在教师引导下学生的“有限再创造”[3]过程。其中，隐性的教学观、有限的再创造都是基数减负的另一种表达，是学生体验数学的认知前提。没有分类建模，“学”将深陷于题海的泥潭；没有数学内部知识的贯通，“学”将在“一盘散沙”中劳而无用。因此，整体地学、结构地学、系统地学是“基数减负”的通用技术，是减轻课业负担的有效行为。其实，早在1958年著名数学家华罗庚和关肇直就指出，“运算能力、逻辑思维能力和空间想象能力是数学的三种基本能力”[4]，这就是分类建模，力图通过“类”思维模式的培养，提高“学”的质量，减少“学”的基数，促进数学纵向贯通的目标实现。

为此，在数学教学过程中，需要做好以下分类建模工作：一是坚持整体教学观，既教知识又教方法；二是多侧面研究，既教经验又教思想；三是在元认知体验中，将知识经验上升为数学能力。这样，方能在分类建模中促进数学世界内部知识关系的贯通性，减负基数、减少重复，提高学的质性。

比如，图2的组织与设计就是三分类建模的一种哲学视角，力图让学生在减负基数的同时获得数学能力的发展。其中，问题(1)旨在让学生揭示几何体特征的过程中，建立个体概念经验和事实经验，揭示整体教学观的价值；问题(2)则是让学生在多角度分类的过程中建立一类数学模型，反映不同层面研究数学的课程观。同时，纵观问题(1)到问题(2)的过程，则是将知识经验上升为思想方法的通用路径，是将个体经验上升为客观经验的一种表现，是“知识结构”转化为“认知结构”的有效方法。

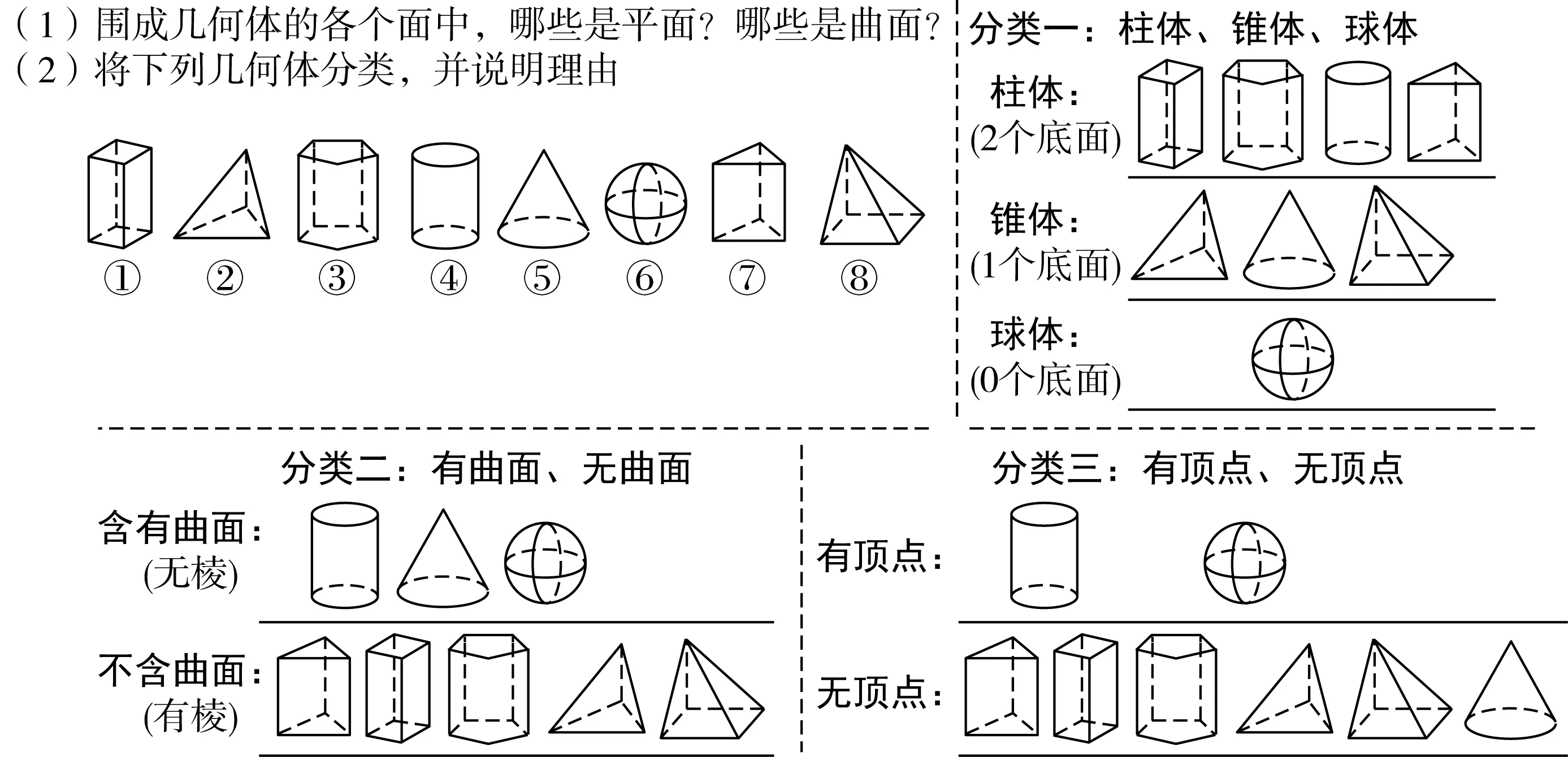
图2 三分类建模

这里需要指出的是，结构化学习、整体观学习、支架式学习以及产生式学习，都带有一定层面的分类建模行为特征，是基数减负的基本方法，是贯通数学世界到数学世界的有效行为。其中，结构化、整体观、支架、产生式、命题、图式等程序性操作，都是基数减负的一种教学行为，是学生学好数学、学优数学的内部思维支持条件。

三、第三阶：超回归编码，通过增值迁移建立数学世界与育人世界的基本面

数学理解是数学教育的目的和目标。“超回归编码”就是在回归数学概念、回归数学理解、回归数学的思维发展、回归数学知识的生长与人的成长并重发展的过程。超回归编码是以超回归理解模型的建立为支架的，而超回归理解模型由原始认识、产生表象、形成表象、性质认知、形式化、观察述评、构造化、发明创造八个不同理解水平构成，这八个层次性理解水平，反映了人们认识某一数学知识的全过程。其中，原始认识、产生表象、形成表象三因素属于“超回归编码”的思维起点，性质认知、形式化、观察述评三因素是增值迁移的心理基础，构造化、发明创造是数学世界与育人世界的一个基本面，包括理性具体、理性一般以及理性中的具体等数学育人要素。从教育学看，史宁中教授把其解释为数学的“三个世界”，通常用行为动词“三会”来描述“三个世界”的本意。也就是，把“会用数学的眼光观察现实世界、会用数学的思维思考现实世界、会用数学的语言表达现实世界” 归结为发展核心素养的思维本体论。

比如，在研究“丰富的图形世界”的过程中，不仅要从众多的城市建筑物中抽象出常见的几何体(思维起点)，还要研究常见几何体的特征及其新定义概念的合情、合理、合法属性(增值迁移)，更要研究常见几何体的多侧面分类(数学育人、基数减负)，并研究常见几何体的物理空间，以此揭示“数学研究对象是数量关系和空间形式的科学”(恩格斯语)。

数学教育的本意就是人的充分发展问题。基数减负、增值迁移就是为了促进人的发展。朱德全对教学本质进行哲学思考后指出，“人的发展促成问题解决，问题解决指向人的发展”[5]。通过超回归编码来建立数学世界与育人世界的基本面是数学课堂教育的根本任务和数学教育的目的，是数学课堂教育落实“双减”政策的有效路径。数学课堂作为育人的主阵地，总是以问题解决为载体，通过优化问题解决路径，灵活调用知识关系，实现减负增效，进而促进学生原本应有的内在成长。这里的“基数减负”不止于少做题，既在于多思考，更在于“同构、贯通、联系”，拓展思考的深度、广度和厚度。比如，图3中设置的“游戏数学活动”就是学生全程体验几何体概念特征的有效设计，是对问题解决的二次升级，突出同构，是学生理解数学模型水平的一项硬性指标。

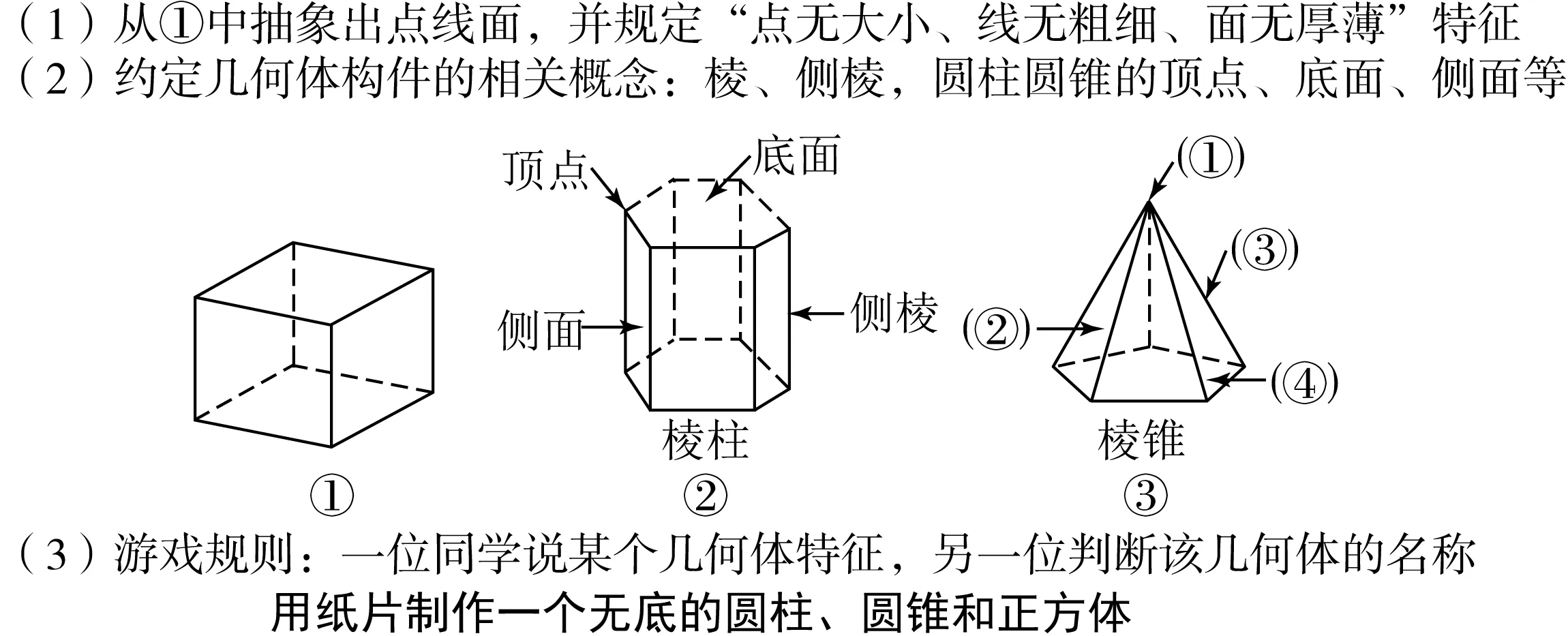
图3 超回归编码

当然，问题解决是超回归编码的心理支架，是揭示数学世界与育人世界的基本面的思维方式，是减负增值的载体。从认知心理学角度分析，“问题解决就是解题者在元认知调控下，对问题进行表征，对问题模式进行识别，然后在自己的长时记忆中提取解题图式并迁移到新的问题情境，进而达到目标状态的信息加工行为”[6]。

就这一认识来说，超回归编码需要处理好以下数学育人关系，方能减负增值、增值迁移，给学生带来更多的数学成长时空。一是问题解决需要与学生的当前数学心理水平一致；二是问题组块适合“场独立”学生“跳一跳”，“场依存”学生“跳三跳”以及“场一般”学生“够得到”；三是通过“同构”和“异构”的思维方式，让学生在元认知活动中建立问题空间和直觉的“超回归”发展，进而减负做题、增值思考、增值表达、增值数学方法，并获得“带得走”数学课堂的能力和终身数学发展的能力。

比如，图3中的问题(1)(2)就属于适应学生当前数学心理水平发展的好问题，有助于学生在回归概念中增值理解；图3中的问题(3)有助于“场依存”学生够得到，有助于“场独立”学生学得好。同时，制作几何体的问题设计与实施，是基数减负的常见思维方式，有助于聚焦思考目标、贯通思考过程，有助于发展学生的问题空间，提高直觉的创造功能。

有学者指出，直觉比以往任何时候都更加成为数学发现的创造源泉。问题空间是以直觉为基础的，通过联想和想象建构完整的知觉活动，并在二次反思和元认知的条件下，形成一定层面的逻辑活动和理性中的具体。其中，二次反思和元认知活动就是基数减负不可绕开的途径。没有反思就没有知识关系的建立和直觉的进步，没有二次反思就没有数学世界与育人世界的基本面的建立，没有元认知就没有整体观念的建立和人的充分发展。

比如，“情境抽象→折几何体→摸几何体→制作几何体”就是以直觉思维为心理基础的，是建立问题空间的一个常见例子，反映了认识几何体的超回归目标。其中，抽象是一种概括表达和反思表达，“折”是做中学、做中思和做中揭示特征的直觉思考方式，而由“摸→制作”是二次反思和元认知监控的问题空间，是学以致用、贯通思维、建立结构的通用技术。因此，数学世界到育人世界是以“直觉”和“问题空间”为思维支架的。具体来说，问题空间(状态空间)，是指任务范围的内部心理表征，包括对目标、现有状态与目标状态的差别、可以执行哪些操作等理解。源于此，在超回归编码过程中，问题设置要预留足够的思维空间，让每一个学生在能表达中获得各自的表达能力，问题解决要让学生在反思中反思，在反问监控中提高元认知能力，进而提高学的目的性，减负问题基数、增值经验。

最后，在这里还需要指出，减负是一种行为目标，更是一种数学教育观念，只有数学老师的育人观念提高了，减负的本意才会“如我们所愿”。▲