电力全要素碳排放效率及收敛性研究

2022-04-06王喜平王素静

电力科学与工程 2022年3期

王喜平，王素静

（华北电力大学经济管理系，河北保定 071003）

0 引言

电力行业在社会经济发展中具有支柱性作用，同时也是我国碳排放的主要来源。电力行业碳排放在全国占比超过 40%，其碳减排效果对我国整体碳减排目标的完成具有直接影响。我国不同区域在经济水平、技术条件、资源禀赋等方面具有显著差异，电力生产技术存在较强的异质性。这意味着要促进电力行业碳减排必须准确测算不同区域的电力碳排放效率并深入分析其增长来源。

在低碳化发展背景下，碳排放效率的测算问题受到国内外学者的密切关注。学者们大致从单要素和全要素2个视角对碳排放效率进行测算。文献[1]使用单要素碳生产率（即单位二氧化碳的GDP产出）对我国碳生产率进行研究。这一概念虽简单易懂，却忽略了能源、劳动、资本等要素的综合影响。使用基于前沿函数的全要素生产效率，能更加全面准确地测算碳排放效率。目前构造生产前沿的方法主要有2种：一种是随机前沿分析（SFA）。比如，文献[2,3]考虑多投入产出要素，运用SFA方法对我国碳排放效率进行研究。SFA方法虽然考虑了多投入产出要素，但其单调性假设可能被拒绝；因此，目前最常用的是数据包络分析（DEA）方法。为了对决策单元在生产过程中效率的动态变化及其驱动因素进行分析，Malmquist-Luenberger（ML）生产率指数，将Malmquist生产率和含非期望产出的方向距离函数相结合；该方法在动态效率的测算和分解方面具有显著优势[4-6]。

由于传统的ML指数不具有传递性，因此文献[7]考虑到全局跨期技术前沿，提出 global Malmquist-Luenberger（GML）。GML指数具有循环累积性，避免了不可行问题；但该指数没有考虑到不同决策单元在投入产出过程中的技术前沿差距，忽略了区域间的技术异质性，因此需要引入共同前沿理论对碳排放效率进行全面分析。为此，文献[8]基于GML指数构建了Meta-frontier GML（MGML）指数。

近年来，共同前沿理论被广泛应用于碳排放效率的测算。文献[9]从技术异质性角度构建了共同前沿ML指数对环境效率进行了测算。文献[10]构建共同前沿全要素碳生产率，测算了2005—2015年我国省际工业碳排放效率。文献[11]用共同前沿 MGML指数测算了我国工业环境全要素生产率。文献[12]针对我国高耗能产业，构建了共同前沿 Malmquist碳排放效率指数，并将其分解为效率变动、技术变动和追赶效应3部分。文献[13]运用共同前沿非径向Malmquist指数，对我国钢铁碳排放效率进行研究。

在电力行业效率评价方面，学者们主要研究了电力行业整体环境或技术效率，而专门针对CO2排放效率的研究较少。文献[14]把发电量作为产出变量，运用Metafrontier模型对我国电力产业区域技术效率进行比较分析，结果表明：东西部地区效率高于中部。文献[15]将SFA和DEA方法相结合，基于3阶段DEA模型测算了火电行业技术效率，结果认为：环境因素和随机因素对投入冗余具有显著影响。文献[16]将电力行业CO2、工业SO2排放量和烟粉尘量共同作为非期望产出，采用超效率SBM-GML模型来衡量电力行业区域环境效率；研究表明：环境效率总体呈上升趋势且空间上由东南向西北递减。该研究仅把 GML指数分解为技术效率和技术进步，但忽略了技术差距的影响。文献[17]利用 DEA-Malmquist指数对我国电力全要素碳排放效率进行测算；但该研究没有将技术异质性考虑在内，且没有对增长来源进行深入分析。

对于电力行业碳排放效率的测算，现有的研究通常假设不同省份具有相同或相似的生产技术。然而，我国各区域在经济发展、资源禀赋、电力系统内部等方面的差异，使得不同地区能够实现的潜在最佳生产技术因生产前沿的多样性而不同。位于不同地区的省份可能存在不同的生产前沿，不同地区可以实现的潜在最优生产技术也各不相同。如果忽略技术异质性，研究结论就会产生偏差，从而很难找到差距产生的真正原因，最终误导决策。此外，将不同地区的省份放在不同的生产前沿下进行比较，如果缺乏统一的标准，则会导致不同地区的省份之间的电力碳排放效率不具有可比性。

鉴于使用 MGML指数可以确定不同地区之间的技术差距并使之具有可比性，在现有研究的基础上，本文进行了以下扩展：构建 MGML指数，从动态角度更加全面准确地测算我国电力全要素碳排放效率；考虑技术异质性的影响，将MGML指数分解为技术效率变化指数（EC）、技术进步指数（BPC）和技术差距比率变化指数（TGC），以深入揭示电力全要素碳排放效率的增长来源，分析其区域差异与动态演化；最后利用收敛性检验，分析这种差异是否会进一步扩大，从而为我国电力全要素碳排放效率的提升提供相关建议。

1 研究方法与数据来源

1.1 研究方法

1.1.1 非期望产出的SBM模型

DEA通过数学规划将决策单元向生产前沿进行投影，然后通过比较决策单元与前沿面的距离来评价其有效性。传统的DEA没有考虑环境等负面因素的影响，也忽略了投入产出的冗余和不足问题，使得测度值可能有所偏差。

本文采用包含非期望产出的 SBM 模型测算效率。将发电过程中投入冗余、期望产出不足、非期望产出冗余带来的松弛性问题纳入目标函数和约束，以更加准确地测算效率值。模型建立如下。

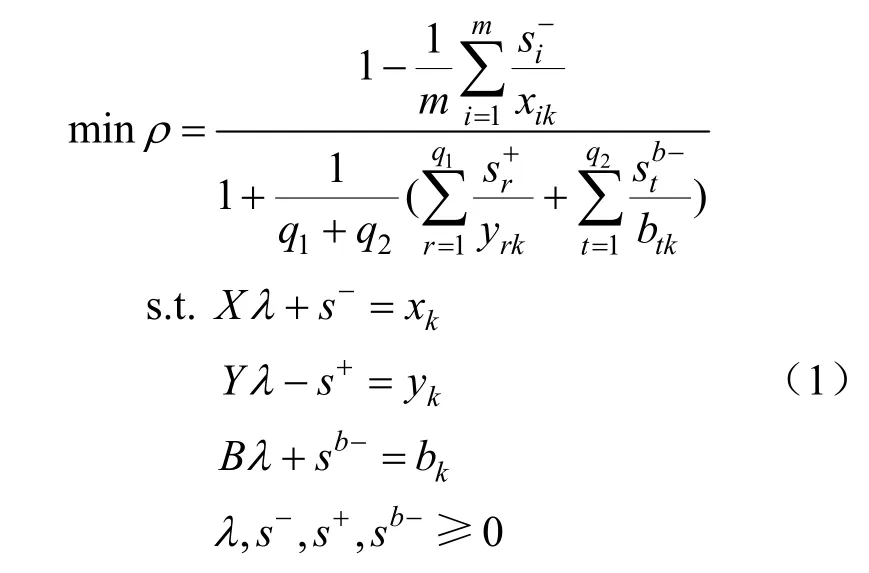
在本文算例中：将每个省份视为一个决策单元（DMU）。用m、q1、q2分别表示DMU投入种类数量、期望产出种类数量和非期望产出种类数量。用xik、yrk和btk分别表示投入、期望产出和非期望产出的量。用分别表示投入冗余、期望产出不足和非期望产出冗余。λ为常数量。ρ越大，表示效率值越高；效率值为1表示决策单元处于有效状态。

1.1.2 MGML指数

GML指数被广泛应用于动态效率的测算。考虑到我国各地区电力生产技术的异质性，本文构建MGML指数，从动态角度衡量我国电力全要素碳排放效率。

在共同前沿方法中，技术缺口比率（TGR）为共同前沿技术效率与群组前沿技术效率的比率，表示共同前沿与群组前沿技术水平之间的差距。本研究中MGML指数可以定义为：

式（2）将电力全要素碳排放效率解构成3个因素。EC表示t期到t+1期群组技术效率变化，反映了技术落后地区向先进地区的追赶程度，可视为“追赶效应”。EC大于1表示技术效率提高，反之则下降。BPC表示t期到t+1期群组当期前沿与群组跨期前沿的接近程度，可视为“创新效应”。BPC大于1表示技术进步，反之则为技术退步。TGC表示t期到t+1期群组跨期前沿与全局跨期前沿之间的技术差距变化率，可视为“领先效应”。TGC大于1表示群组跨期前沿与全局跨期前沿之间的差距缩小，反之则扩大。

1.1.3σ收敛

本文使用变异系数来进行标准差σ收敛检验。若变异系数随着时间的推移趋于下降，则说明存在σ收敛现象。σ计算公式为：

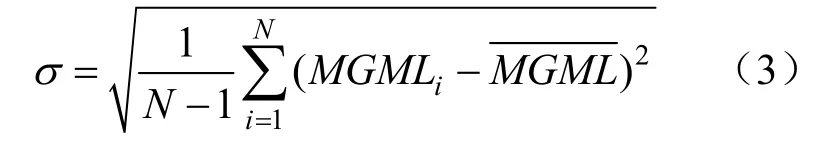
式中：MGML表示i地区的电力全要素碳排放效率指数；表示各地区电力全要素碳排放效率指数的平均值；变异系数

若t+1期的变异系数比t期小，则存在σ收敛。

1.1.4β收敛

运用以下模型进行电力全要素碳排放效率的绝对β收敛检验计算：

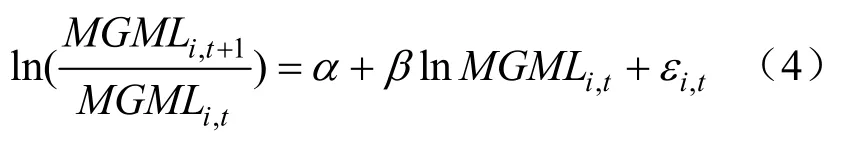
式中：MGMLi,t和MGMLi,t+1分别表示地区i在某一时段基期和末期电力全要素碳排放效率水平；表示基期到末期年均电力全要素碳排放效率增长率；α为截距项；εi,t为随机误差项。若式中β显著为负，则表明电力全要素碳排放效率存在绝对β收敛，收敛速度为λ=-ln（1+β）。

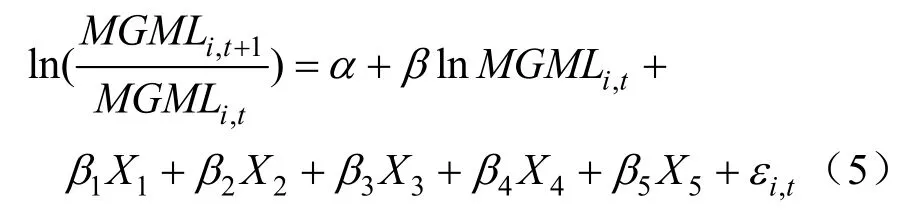
本文在绝对β收敛检验的基础上，进一步对我国电力全要素碳排放效率变化是否存在条件β收敛进行检验。综合相关文献，选用以下5个因素作为控制变量代入模型，即可得到条件β收敛检验模型：式中：X1、X2、X3、X4、X5分别代表经济发展水平（地区实际GDP，以2003年为基准换算）、城镇化水平（城镇人口占总人口比重）、发电结构（火力发电量在发电总量占比）、电耗强度（用电总量除以GDP）、环境规制（工业污染治理投资完成额占GDP比重）。

1.2 变量选择与数据来源

选取我国30个省（市、区）的电力全要素碳排放效率相关数据，使用MaxDEA软件进行测算。基础数据全部来自2003—2019年《中国统计年鉴》《中国电力年鉴》《中国能源统计年鉴》。

由于火力发电是电力行业碳排放的主要来源，因此以火力发电相关数据进行测算。

将资本、劳动和能源作为投入指标，火力发电量作为期望产出，发电碳排放量作为非期望产出。资本投入用发电装机容量表示。由于没有单独的针对电力行业的就业人数统计数据，本文采取和电力行业相近的电力、热力生产和供应业的就业人数对其表示。能源投入为火力发电消耗的能源，用发电标准煤耗与火力发电量的乘积来对其表示。对于电力行业碳排放量的计算，本文采用IPCC提出的碳排放测算法。对火电生产消耗的8种主要能源进行测算，计算公式如下：

式中：PCO2表示电力行业二氧化碳排放量；i表示化石能源种类；PE,i表示能源消费量；PEF,i表示碳排放系数；PNCV,i表示平均低位发热量；PCEF,i表示平均热值含碳量；PCOF,i表示碳氧化率；44/12是分子量比值。8种主要能源包括煤炭、焦炭、原油、汽油、煤油、柴油、燃料油、天然气。

2 电力全要素碳排放效率及动态演变趋势

2.1 省域MGML指数及其分解效应

表1所示为我国分地区MGML指数及其分解结果。

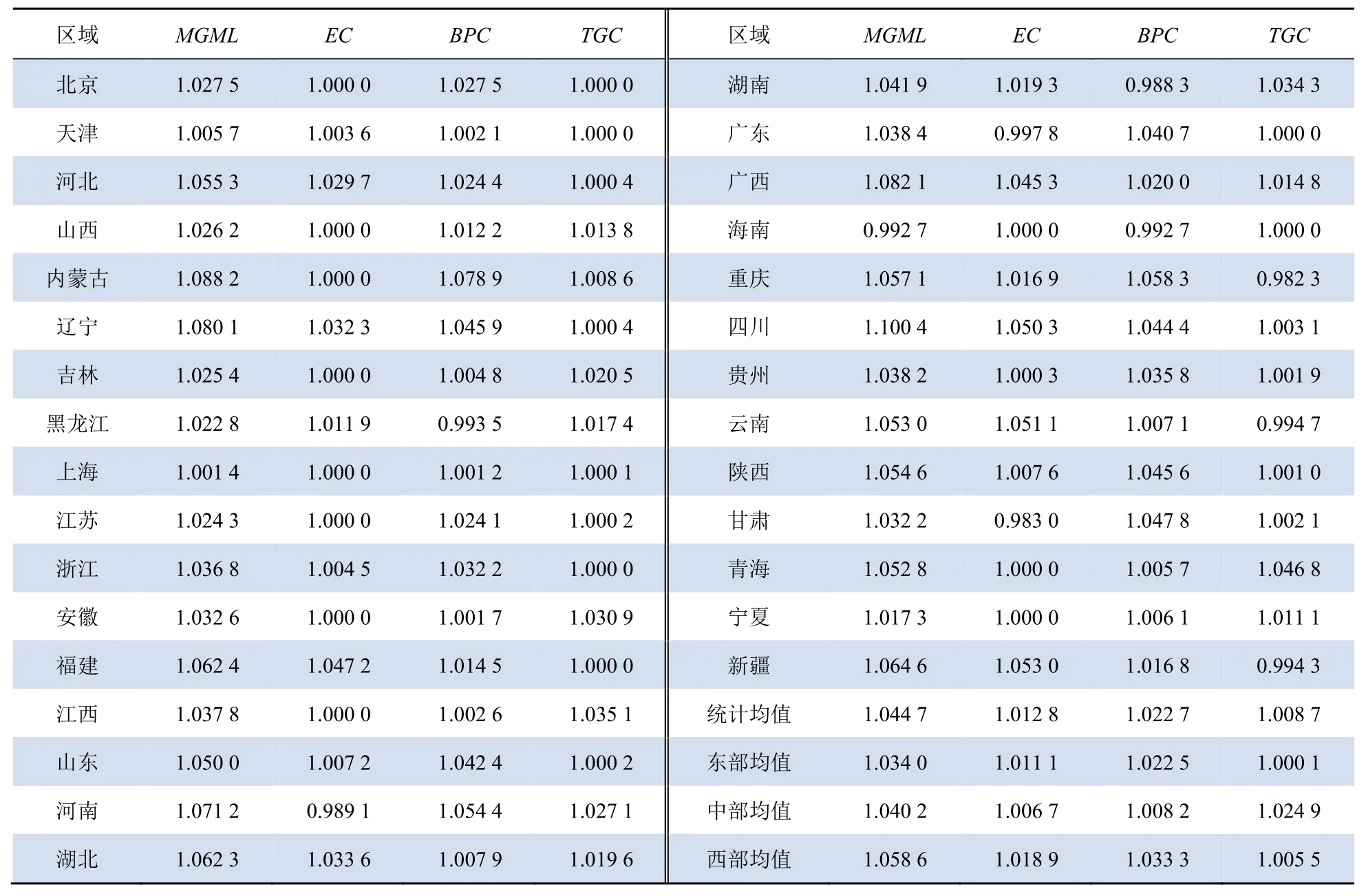
表1 分地区MGML指数及其分解Tab. 1 Regional MGML index and its decomposition

对表1数据进行计算分析。

我国电力全要素碳排放效率在样本期内以年均4.47%的速度增长，且大多数省份MGML均值都大于1，可见我国电力行业在节能减排方面取得了显著成效。各省增长速度差异较大，其中四川年均增速高达 10.04%，海南则低至-0.73%。因此，需要进一步从技术效率、技术进步、技术差距等方面分析造成电力全要素碳排放效率增长差异的原因。

从分解效应来看，EC指数年均增长1.28%，技术效率的改善反映了当前我国大多数省份的电力行业资源配置效率逐渐提高，且在管理模式与制度安排等方面也得到优化。BPC年均增长2.27%，这表明随着时间推移，群组当期前沿逐渐趋近于群组跨期前沿，区域实际电力低碳生产技术已经逐渐靠近区域潜在最优技术水平，技术创新效应比较显著。TGC年均增长0.87%，说明我国区域潜在最优电力低碳生产技术与全国潜在最优电力低碳生产技术之间的差距在不断缩小。综上可知，电力全要素碳排放效率增长主要来源于技术创新，而技术效率和技术差距变化的贡献较小。

从3大区域来看，MGML指数呈现西—中—东递减的趋势。东部地区电力全要素碳排放效率增速低于平均水平。东部地区改革开放早且发展迅速，电力生产技术已经处于全国领先水平，上升空间不大从而增长较慢。中西部地区电力全要素碳排放效率增长速度均高于东部地区，这是因为：中西部地区原本电力生产技术比较落后；近年来通过学习东部发达地区的技术经验，加上充分利用能源资源优势发展清洁能源发电，电力碳排放效率得到显著提升。从各区域分解效应来看，3大区域EC、BPC和TGC均值都大于1，可见各地区在管理效率、制度安排和技术创新水平都有了一定的提高。东西部地区BPC指数较大，表明技术创新是电力全要素碳排放效率增长的主要动力。

近年来我国不断推进电力行业节能减排技术以及低碳技术的改革与创新，电力碳减排成效显著。从TGC指数可知，我国3大地区的区域差距在不断缩小，逐渐趋近于全国最优生产技术水平。

总体而言，电力全要素碳排放效率呈增长态势，MGML指数呈现西—中—东递减的趋势，区域差距有所减小。3大区域电力全要素碳排放效率增长来源不同：东西部地区主要依靠技术创新驱动，中部地区的效率增长则主要来源于技术差距的缩小。

2.2 MGML及其分解指数的动态演变趋势分析

图1所示为我国3大区域MGML指数的变动趋势。

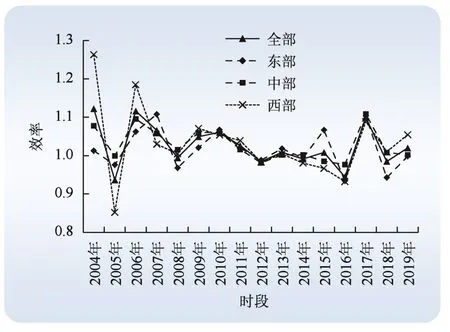
图1 3大区域MGML指数的变动趋势Fig. 1 Change trend of MGML index in three regions of China

由图1可以看出，MGML指数波动较大，大部分年份为正增长。2003—2004年MGML指数增长幅度最大，达到12.21%；这与 2003年国家颁布了一系列保护资源环境的政策与措施，促使电力行业高度重视CO2减排工作有关。2011—2016年，电力全要素碳排放效率持续下降，2016年达到谷底，分析其原因为：在此期间，城市化进程的加速给电力行业碳减排工作带来了巨大压力。在“十三五”规划期间，政府高度重视电力行业碳减排工作，2015年出台的《关于进一步深化电力体制改革的若干意见》促使了新一轮改革路径探索。于是，从图1可以看到，2015年之后，MGML指数有所回升。

我国不同区域在不同阶段的发展极不平衡，电力全要素碳排放效率动态变化趋势也存在较大差异。总体来看，3大区域MGML指数的变化呈现较大的波动性。东部地区MGML指数在大多数年份都大于1，中西部地区的电力全要素碳排放效率的增长则比较低迷，整体呈现波动下降趋势。

图2所示为电力全要素碳排放效率及其分解指数的变动趋势。

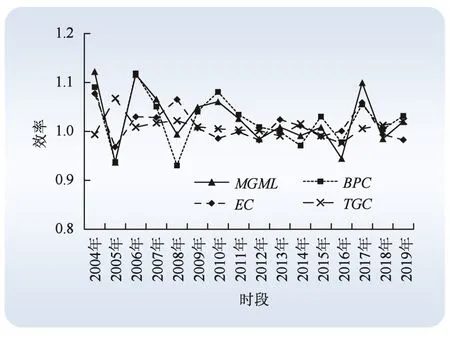
图2 电力全要素碳排放效率及其分解指数变动趋势Fig. 2 Change trend of total factor carbon emission efficiency of power industry and its decomposition index

由图2可知，MGML和BPC指数的变化趋势几乎一致，这再次说明技术创新是电力全要素碳排放效率提升的关键。

图2中，TGC指数呈现波动上升趋势，而EC和BPC指数都表现出波动下降趋势，其中BPC指数波动幅度最大。对EC和BPC指数的演变趋势进行比较发现，技术效率和技术进步没有实现齐头并进，甚至出现相互背离的增减趋势。导致这种现象产生的原因应在于：在所分析的数据期，电力低碳化发展主要依靠的是资金和技术投入，而忽视了资源配置效率的提高，存在电力价格扭曲、财政体制缺陷、管理模式落后以及人力资本水平较低等诸多缺陷，进而造成了技术效率变化与电力全要素碳排放效率增长背道而驰的现象。因此，在实践中应该积极推进协调良性发展，共同推动电力全要素碳排放效率的提高。

图2中，不同于EC和BPC指数的大幅波动，TGC指数变化非常平稳，大部分年份均稳定增长，这说明：我国地区之间电力低碳生产技术差距在不断缩小，全国范围内的电力全要素碳排放效率存在收敛现象。

3 电力全要素碳排放效率收敛性分析

由上述分析可知，不同区域之间电力碳排放技术的异质性导致电力全要素碳排放效率存在显著差异，TGC指数显示区域差距有所减小。为了进一步检验这种差距是否会随时间的推移而缩小，本文分别采用σ收敛、绝对β收敛和条件β收敛模型对电力全要素碳排放效率的收敛性进行分析。

σ收敛检验结果如图3所示。

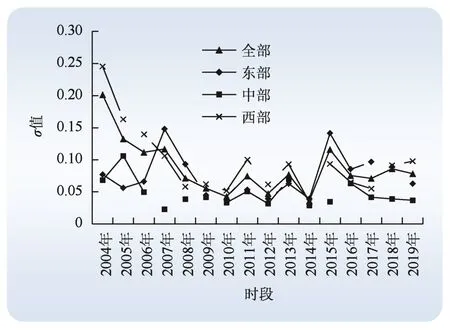
图3 电力全要素碳排放效率σ收敛Fig. 3 σ convergence of total factor carbon emission efficiency of electric power

由图3可知，中西部地区MGML指数标准差均存在σ收敛，这表明：中西部地区电力全要素碳排放效率区域差距在逐渐缩小，而东部地区电力全要素碳排放效率差异将继续存在。

此外，对各地区MGML指数的变异系数进行横向比较发现，西部地区MGML指数的变异系数均值最大（0.094 8），东部次之（0.074 4），中部最小（0.047 2），这说明西部地区电力全要素碳排放效率的内部差异最大。原因分析：西部地区内部的各省经济发展水平及环境状况差异较大，既有经济较发达的四川、重庆、陕西，也有欠发达的新疆、青海、西藏；西部大开发政策的实施更是扩大了这种差异。东部地区大部分为沿海发达地区，但各省之间的经济水平和环境条件差距明显。相比较而言，中部地区各省发展水平相当，在经济基础、环境状况及发展战略方面大同小异，使得电力全要素碳排放效率区域差距较小。

绝对β收敛检验结果如表2所示。由表2可见，3大区域的β值都显著为负，这表明：3大区域电力全要素碳排放效率都存在绝对β收敛，各地区电力全要素碳排放效率能够趋向相对同步增长，区域差距在不断缩小。由于收敛速度λ与β绝对值呈正相关，因此可知东部地区收敛速度最快，西部地区次之，中部地区最慢，其原因在于：中部地区在经济发展、技术条件及资源禀赋方面没有明显优势；东部地区得益于优越的地理位置和较好的经济基础；西部地区则得益于国家的政策倾斜，例如西部大开发。

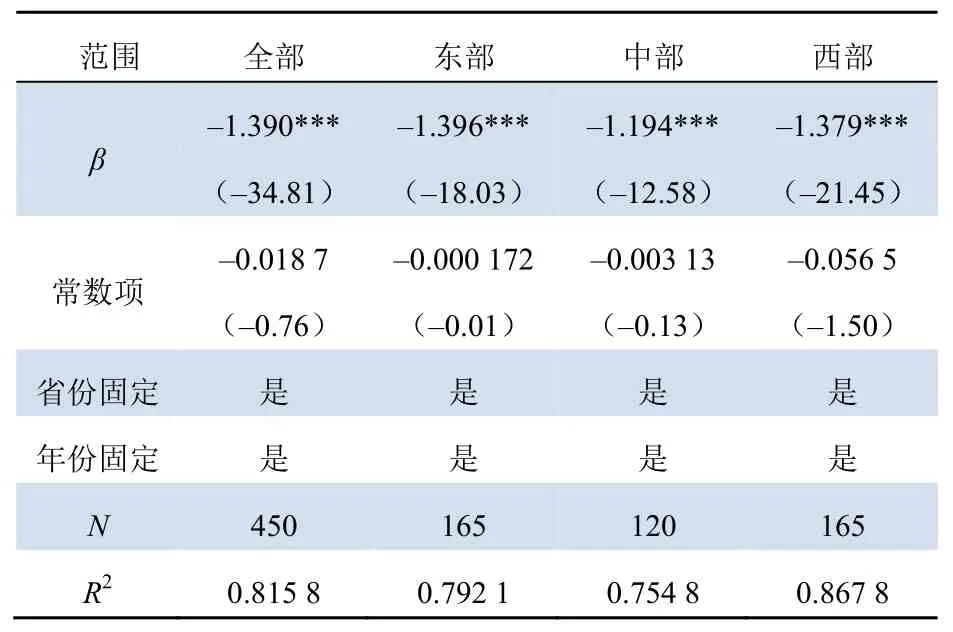
表2 绝对β收敛检验Tab. 2 Absolutely β convergence test

条件β收敛检验结果如表3所示。由表3可知，在加入控制变量后，东、中、西部地区系数β仍然显著为负，这说明：电力全要素碳排放效率存在条件β收敛，也即表明各区域电力全要素碳排放效率会随着时间的推移趋向于各自的稳态水平。由于各地区在生产技术方面的改进和管理效率的提升，各地区差距明显缩小；收敛速度同样呈东—西—中递减的趋势，分析其原因为：中部地区各省份发展政策及条件相似，本身差异不大，因此向自身稳态水平收敛的速度相对较慢；而东西部地区各省份内部条件存在较大差距，通过近几年的快速发展，差距不断缩小，收敛速度相对较快。建议：通过适当政策措施促进区域效率的稳态值趋于一致，缩小区域差距。

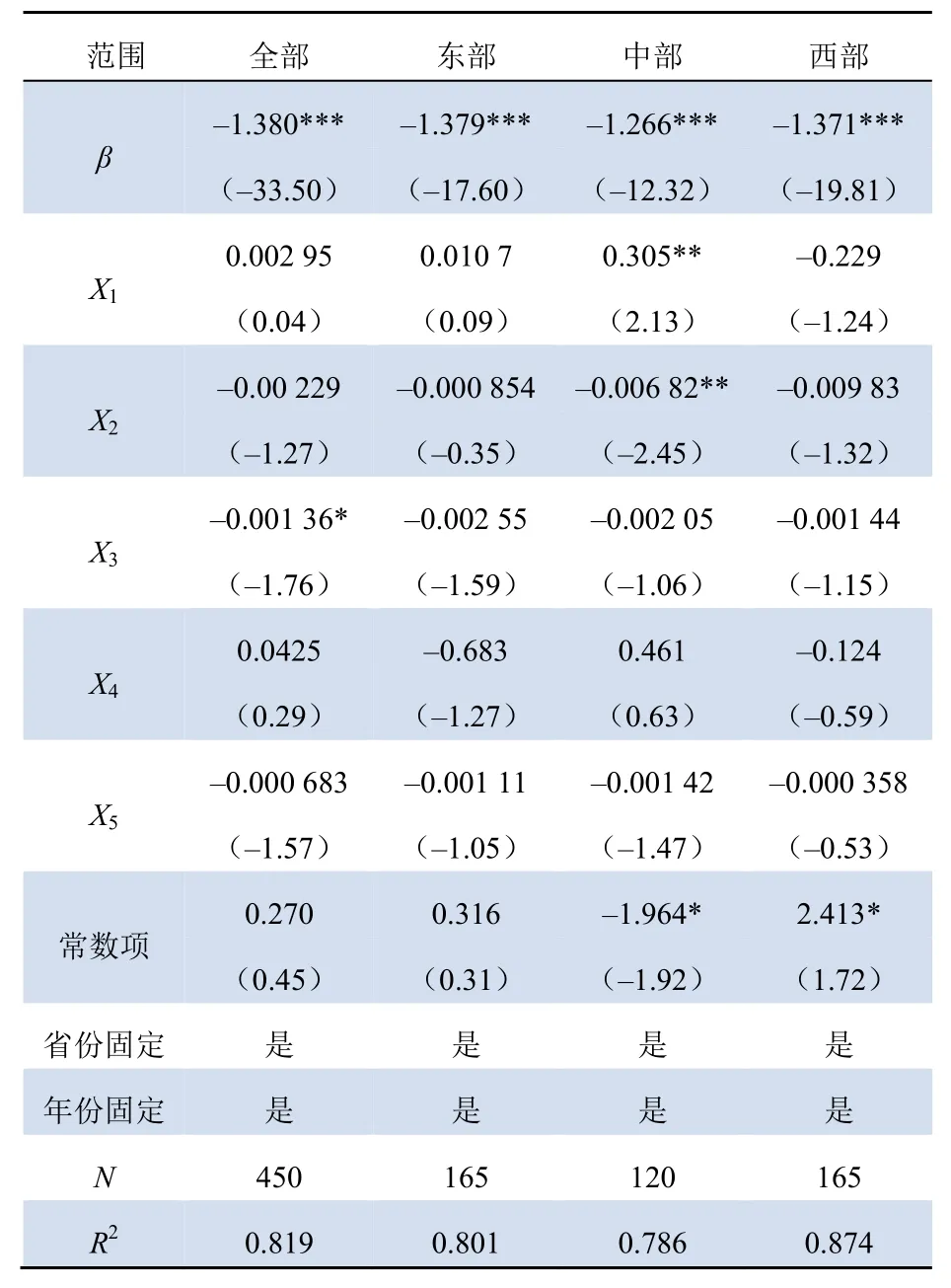
表3 条件β收敛结果Tab. 3 Conditional β convergence test

4 结论

4.1 研究结论

由于各地区社会经济发展极不平衡，经济水平、技术条件和资源禀赋等方面存在较大差异，导致区域电力生产技术存在明显的异质性。

本文在技术异质性假定下，基于2003—2019年各地区面板数据，运用MGML指数对电力全要素碳排放效率进行测度并将其分解为技术效率变化指数、技术进步指数和技术差距比率变化指数，揭示了全要素碳生产率增长的来源，在此基础上分析其区域差异及动态演化，最后通过σ收敛和β收敛模型分析电力全要素碳排放效率的收敛性。主要结论如下：

（1）我国电力全要素碳排放效率总体呈增长趋势，年均增速为 4.47%，大部分省份电力全要素碳排放效率均表现为正增长。技术创新是促进电力全要素碳排放效率增长的主要原因，而技术效率提升和技术差距缩小的贡献相对较小。

（2）3大区域电力生产技术存在明显的异质性。电力全要素碳排放效率呈西—中—东递减的增长趋势且各区域增长来源不同。东西部地区电力全要素碳排放效率的增长依赖于技术创新，中部地区效率增长则主要来源于技术差距的缩小。

（3）中西部地区电力全要素碳排放效率均存在σ收敛特征。3大区域均存在绝对β收敛和条件β收敛，这说明各地区在朝着稳态水平趋近的同时区域差距也在逐渐缩小。