弹性基上圆柱管弯曲行为的高阶剪切梁理论解*
2022-04-06马维力申柳雷宋殿义李显方
马维力,申柳雷,宋殿义,李显方
(1. 长安大学 理学院, 陕西 西安 710064; 2. 国防科技大学 军事基础教育学院, 湖南 长沙 410072; 3. 中南大学 土木工程学院, 湖南 长沙 410075)
作为工程结构中最常用的构件,梁被广泛应用于土木工程、航空航天、医疗卫生等领域。如埋入地基中或放置于地基上的输油、输气、输水管道等。随着工程技术不断发展,各个行业不断探索追求构件的轻量化设计,在满足结构强度、刚度和稳定性的前提下,尽量降低结构件自身重量。与实心圆柱梁相比,相等重量的圆柱管具备更强的抗弯能力和抗扭能力,成为更优的选择。
关于梁理论的研究可以分为两种处理方法,一种是当作三维弹性问题求解,这种方法求解精度高,但方法复杂,对于一些复杂边界条件问题甚至无解[1-3];另一种是合理简化为一维弹性问题,这种方法求解简单,便于工程应用。基于第二种方法,有著名的Euler-Bernoulli梁理论、Rayleigh梁理论和Timoshenko梁理论等经典梁理论。其中,Euler-Bernoulli梁理论未考虑横截面的剪切变形和转动惯量的影响[4],而Rayleigh梁理论增加考虑了转动惯量的影响,但未考虑剪切变形的影响[5]。Timoshenko梁理论虽然考虑了剪切变形的影响,但必须引入一个剪切修正系数,且该剪切修正系数不能通过理论自身获得[6],并有各种各样的取值范围。
Levinson[7]首次基于高阶剪切变形梁理论分析了矩形截面梁的力学行为。运用剪切变形梁理论的优点是可以考虑剪切变形和转动惯量的影响,且不需要引入剪切修正系数,同时满足表面剪应力为零的边界条件。Huang等[8-9]将Levinson梁理论的适用对象拓展至圆形截面梁。She等[10]基于Euler-Bernoulli梁理论、Timoshenko梁理论和多种高阶梁理论,对功能梯度材料梁的热屈曲和后屈曲行为进行了分析。Shao等[11]基于广义剪切变形梁理论,提出了关于复合材料层合梁自由振动的统一分析方法。Arefi等[12]利用三阶剪切变形梁理论,研究了功能梯度纳米梁在电磁弹性载荷作用下的非局部电磁热弹性问题。Heydari[13]基于微分变换法,提出了一种求解耦合偏微分运动方程的新方法,对纳米矩形梁的高阶振动与屈曲行为进行了讨论。Benadouda等[14]在考虑孔隙率的情况下,对梁进行了自由振动分析。基于高阶梁理论,Choi等[15]建立了变截面四边形薄壁梁有限元模型。Selmi[16]利用各种高阶梁理论,对复合梁的静态和模态问题进行了分析比较。Pydah等[17]和Fariborz等[18]通过在环向位移表达式中引入关于径向坐标的对数函数,将适用于长直矩形截面梁的高阶梁理论,推广到圆弧形矩形截面梁。
本文作者建立了适用于圆柱管的高阶剪切变形梁理论,并研究了其振动、稳定性和弯曲波的传播问题[19-21],但是弯曲问题尚未开展研究。本文采用高阶剪切变形梁的思想,推导了弹性基上圆柱管横向弯曲问题的控制方程,并对四种典型边界条件的工况,给出了弯曲问题的解析解。研究了长径比、厚径比等参数对截面应力分布规律的影响。对某些退化情况,与已有文献结果对比,验证了本文结果的准确性。
1 理论公式推导
考虑一个长度为L,内外半径分别为Ri和Ro的圆柱管。为分析其在横向载荷作用下的弯曲问题,需建立笛卡尔坐标系。由于圆柱管具备环形截面,使用柱坐标系比较方便。因此,同时建立笛卡尔坐标系和柱坐标系,如图1所示。
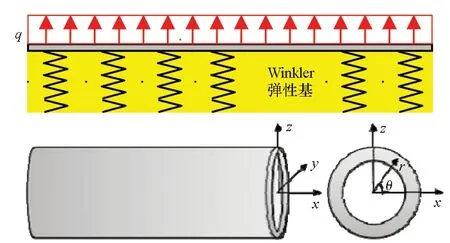
图1 弹性基上圆柱管及坐标系的示意图Fig.1 Schematic of a circular cylindrical pipe bonded to a Winkler elastic foundation with the corresponding coordinates
关于笛卡尔坐标系(x,y,z),其x轴位于变形前圆柱管的中心轴上,z轴的正方向向上,y轴的正方向由右手法则确定。(u,v,w)分别是与(x,y,z)对应的位移分量。关于柱坐标系(x,r,θ),x轴仍位于变形前圆柱管的中心轴上,(x,r,θ)三个方向的位移分量分别用(u,wr,wθ)表示。笛卡尔坐标系与柱坐标系的变量之间存在如下关系:
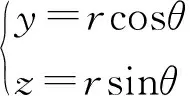
(1)
wr=vcosθ+wsinθ
(2)
圆柱管在横向载荷作用下,在xoz平面内发生弯曲。因此,y方向的位移分量v与变量x无关。与经典梁理论中的处理方式一致,采用圆柱管中心轴在中性层(z=0)的位移分量来描述挠度。所述位移分量w只取决于空间变量x和时间t,即w=w(x,t)。
对于圆柱管,其内外表面属于自由面,剪应力须在内外表面上满足剪应力为零的边界条件,结合胡克定律,可得:
γxr(x,r,θ)=0,r=Ri,Ro
(3)
其中,γxr为剪应变。在柱坐标系下,结合几何方程与式(1)~(2),并假设y轴方向的位移分量v与变量x无关,可得:
(4)
将剪应变γxr写成翘曲形状函数表达式后代入式(4)。此时,轴向位移u的表达式可写成如下形式:
(5)
其中,f(y,z)为截面翘曲形状函数,ψ(x)为截面转角。利用几何方程可得应变表达式如下:
(6)
(7)
按照式(3)要求,剪应力须在圆柱管内外表面保持为零,将式(5)代入式(4)可得:
(8)
基于式(6)和式(7),利用弯矩和剪力的平衡方程,通过简单的计算可将弯矩和剪力分别表示为:
(9)
(10)
其中:
(11)
(12)
(13)
(14)
当圆柱管内嵌在一个弹性基中或者放置在弹性基上时,假设外表面与弹性基之间的相互作用可以通过Winkler关系来模拟。因此,横向分布力、弯矩和剪力满足如下平衡方程:
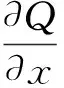
(15)
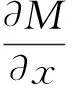
(16)
式中,K为Winkler基的弹簧刚度系数,量纲为N/m2。
将式(9)~(10)分别代入平衡方程(15)~(16),可得:
(17)
(18)
式(17)和式(18)为耦合控制方程。为将其解耦,引入满足方程
(19)
的辅助函数F(x)。只要令
(20)
(21)
将式(20)~(21)分别代入耦合控制方程(17)~(18)中,可以发现它们自动满足。至此,得到了在Winkler弹性基上圆柱管承受分布载荷作用时,弯曲问题的高阶剪切变形梁理论的控制方程(19)。
当不考虑Winkler弹性基,即K=0时,通过积分可得方程(19)的通解形式为:
(22)
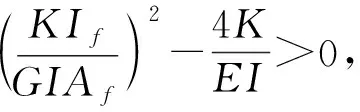
F(x)=A1cosh(λ1x)+A2sinh(λ1x)+
(23)
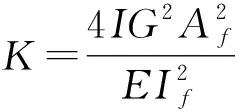
F(x)=(A1+A2x)cosh(λ3x)+(A3+A4x)·
(24)
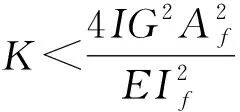
F(x)=emx[A1cos(nx)+A2sin(nx)]+e-mx·
(25)
其中,未知常数Ai(i=1,…,4)可由边界条件求得。λ1、λ2、λ3、m、n的表达形式如下:
(26)
(27)
(28)
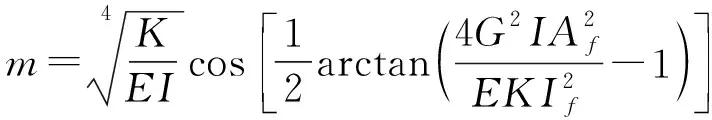
(29)

(30)
2 弯曲问题求解
本节考虑承受四种工况的圆柱管弯曲问题,工况一为Winkler弹性基中承受均布载荷悬臂圆柱管;工况二和工况三分别为自由介质中承受均布载荷的简支和悬臂圆柱管;工况四为自由介质中在自由端(x=L)承受集中载荷P的圆柱管。
取翘曲形状函数f(y,z)为幂函数形式,具体形式如下[20]:
(31)
2.1 均布载荷作用下的悬臂Winkler弹性基圆柱管
工况一为承受均布载荷作用的Winkler弹性基圆柱管,边界条件如下:
w(0)=ψ(0)=M(L)=Q(L)=0
(32)
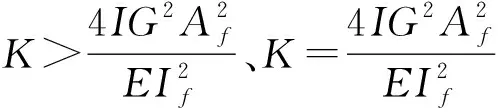
2.2 均布载荷作用下的简支圆柱管
工况二为承受均布载荷作用的简支圆柱管,边界条件如下:
w(0)=M(0)=w(L)=M(L)=0
(33)
将式(9)、式(10)、式(20)、式(21)分别代入式(33)中的各项,可求得未知常数Ai(i=1,…,4),从而得到辅助函数F(x)的表达式如下:
(34)
然后,将辅助函数的表达式代入位移分量和应力分量的表达式,可得位移分量如下:
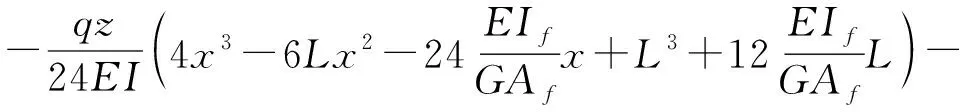
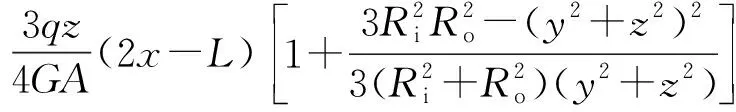
(35)
(36)
(37)
将挠度与转角表达式代入应力分量表达式,可得:
(38)
(39)
(40)
(41)
2.3 均布载荷作用下的悬臂圆柱管
工况三为承受均布载荷作用的悬臂圆柱管,边界条件如式(32)所示。辅助函数的表达式如下:
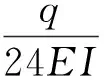
(42)
位移分量的表达式如下:
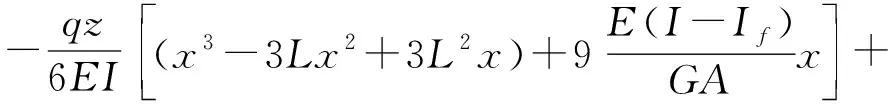
(43)
(44)
(45)
应力分量表达式如下:
(46)
(47)
(48)
(49)
2.4 集中载荷作用下的悬臂圆柱管
工况四为端部承受集中载荷作用的悬臂圆柱管,边界条件如下:
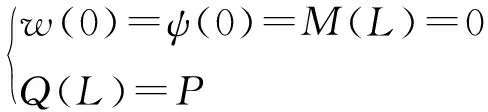
(50)
辅助函数的表达式如下:
(51)
位移分量的表达式如下:
(52)
(53)
(54)
应力分量表达式如下:
(55)
(56)
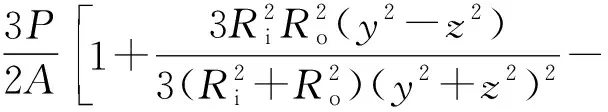
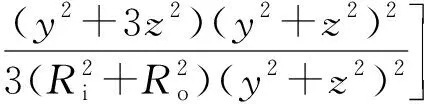
(57)
(58)
从上述四种工况的表达式可以发现,由横向弯曲行为引起的位移和应力分量包括两个组成部分,其中一部分由弯矩引起,另外一部分由剪力引起,并且所有这些结果均依赖于内外半径,尤其是直接检验可以发现内外表面剪应力τxr。假如令剪切刚度GA趋于无穷大,即不发生剪切变形,则上述各项表达式退化到Euler-Bernoulli梁的结果。
3 结果与讨论
3.1 正确性验证
为了验证本文解答的正确性,将本文计算结果与已有文献结果进行对比。以承受均布载荷的简支圆柱管为例,取内外径之比Ri/Ro=0.5,表1给出了不同长径比的圆柱管在梁中间x=L/2截面处的无量纲正应力σxxI/qL3对比。其中文献[22]给出的正应力计算公式为:
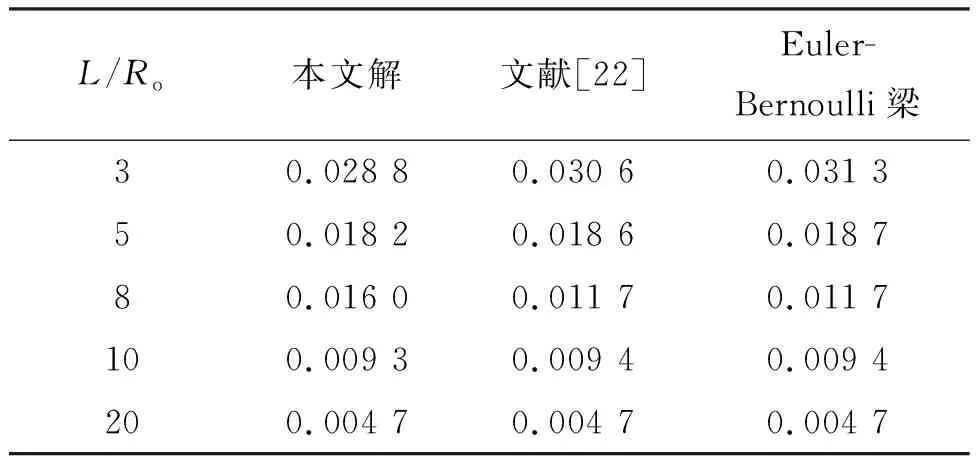
表1 均布载荷作用简支圆柱管正应力(σxxI/qL3x=L/2,y=0,z=0.75Ro)Tab.1 Normal stress σxxI/qL3 of a double simply supported hollow cylindrical tube under distributed load (x=L/2,y=0,z=0.75Ro)
(59)
显然,正应力σxx是变量x和z的函数,但未考虑变量y的影响。而本文所提出的模型中,同时考虑了变量x、y和z的影响。由表1可以看出,当长径比L/Ro≥5时,三种理论计算结果误差较小,当L/Ro<5时,由于未考虑剪切变形的影响,Euler-Bernoulli梁理论对结果过高估计,误差较大,文献[22]次之,本文计算误差最小。
为了验证本文对Winkler弹性基上圆柱管弯曲问题求解的正确性,图2给出了相等均布载荷作用下,不同刚度系数的Winkler弹性基悬臂圆柱管挠度曲线,圆柱管的长径比和内外径之比分别为L/Ro=5和Ri/Ro=0.5。K/E=0时,对应无Winkler弹性基的情况,采用式(44)计算挠度的值。K/E=10-7、K/E=10-10和K/E=10-13对应存在Winkler弹性基,且刚度系数逐渐减小的情况,采用式(25)进行求解得到辅助函数F(x)的值,进一步将其代入式(21)即可得到挠度的值。可以看出,当刚度系数逐渐减小时,圆柱管的挠度逐渐增大。当刚度系数趋近于零时,Winkler弹性基圆柱管的挠度曲线逐渐趋近于无弹性基时圆柱管的挠度曲线,验证了本文关于Winkler弹性基圆柱管弯曲问题求解方法的正确性。
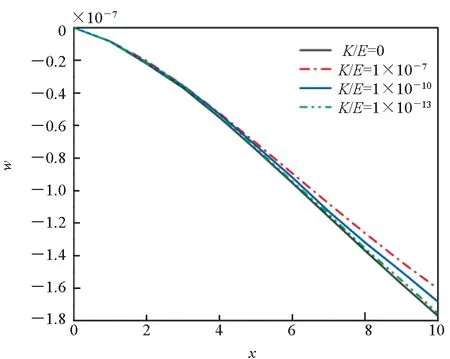
图2 不同刚度系数Winkler弹性基圆柱管挠度分布情况(L/Ro=5,Ri/Ro=0.5 )Fig.2 Effect of stiffness coefficient K on the deflection w of hollow cylindrical tube ( L/Ro=5,Ri/Ro=0.5)
3.2 应力分布情况
图3给出了内径Ri=0,长径比L/Ro分别为2、4和6的简支圆柱管,在x=L/2、y=0处,基于所提高阶梁理论、文献[22]和Euler-Bernoulli梁理论的正应力无量纲参数σxxI/qL3随半径无量纲参数z/Ro的变化情况。当L/Ro=2时,三种理论计算结果相差较大,高阶梁理论和文献[22]的计算结果在变量z方向呈现明显的非线性。
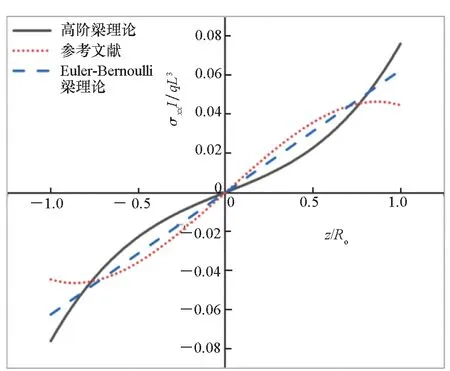
(a) L/Ro=2
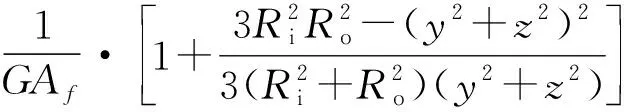
现在考虑一个长径比L/Ro=5,内外径之比Ri/Ro=0.5,泊松比ν=0.3的悬臂圆柱管,在均布载荷q作用下发生弯曲。对于各向同性材料,剪切模量与弹性模量存在如下关系:
(60)
正应力和剪应力可以通过式(46)~(49)确定。图4和图5为悬臂圆柱管在固定端x=0截面处,正应力无量纲参数σxxI/qL3和剪应力τxrA/qL、τxzA/qL在横截面上的应力分布云图。悬臂圆柱管的长径比和内外径比分别为L/Ro=5、Ri/Ro=0.5。观察图4可以发现,在均匀分布力下,轴向应力σxxI/qL3与变量z不再呈线性相关关系,这是因为本文考虑了剪切变形的影响,轴向应力表达式中存在剪切变形非线性相关项,与前文结论一致。从图5中可以发现,剪应力τxr在圆柱管的内外表面为零,圆柱管内外表面为自由表面,这与预期是一致的。另外,在z=0平面上,正应力σxx和剪应力τxr均消失,这是因为应力分布具备对称性。剪应力τxz在远离中间平面z=0时,其应力值逐渐减小,并在靠近顶部和底部位置逐渐消失为零,如图5(b)所示。特别指出的是,应力值在中间平面z=0的内表面达到最大,这意味着中间面内表面位置容易发生剪切破坏。

图4 悬臂圆柱管受均布载荷作用时,x=0横截面无量纲正应力σxxI/qL3分布Fig.4 Distribution of normal stress σxxI/qL3on the section of x=0 of the cantilever hollow cylindrical tube
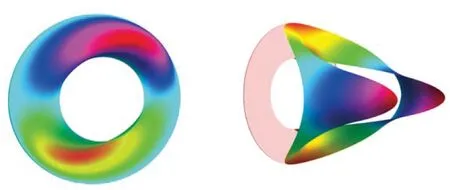
(a) τxrA/qL (b) τxzA/qL图5 悬臂圆柱管受均布载荷作用时,x=0横截面无量纲剪应力分布Fig.5 Distribution of shear stress on the section ofx=0 of cantilever hollow cylindrical tube
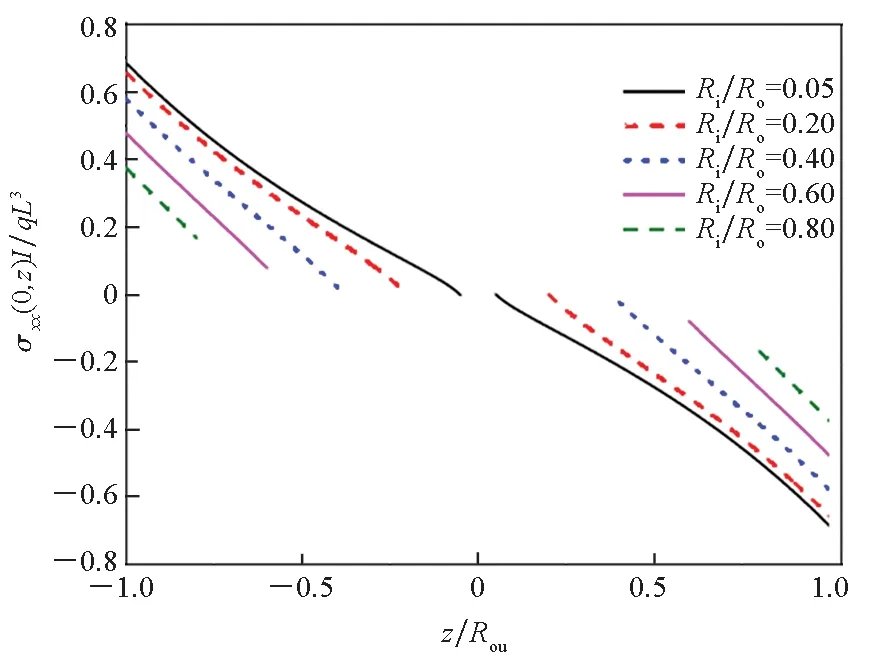
图6 不同内外半径比悬臂圆柱管正应力σxxI/qL3的分布情况(L/Ro=5,x=y=0)Fig.6 Distribution of normal stress σxxI/qL3 of the cantilever hollow cylindrical tube(L/Ro=5,x=y=0)
为了进一步研究应力分布与圆柱管厚度的关系,图6和图7给出了不同内外径比下,长径比为L/Ro=5的悬臂圆柱管正应力无量纲参数σxxI/qL3和剪应力无量纲参数τxrA/qL的应力分布(x=y=0)。当Ri/Ro比值逐渐变大,即圆柱管厚度逐渐变薄时,正应力逐渐呈线性分布;而当Ri/Ro比值逐渐变小,即圆柱管厚度逐渐变厚时,正应力逐渐呈非线性分布。然而,对于任何内外半径之比的圆柱管,内外表面的剪应力τxr始终为零。这一规律具有一定的工程应用价值。例如,城市立交桥梁建设过程中用到的连续板梁结构,受到交通和外观等条件限制,有时需要选择跨度较小的现浇混凝土空心板梁结构,其空心率一般在20%~30%之间。这种结构符合长径比较小且厚径比较大的特征,对其进行强度校核计算时,本文方法可以提供可靠的参考依据。
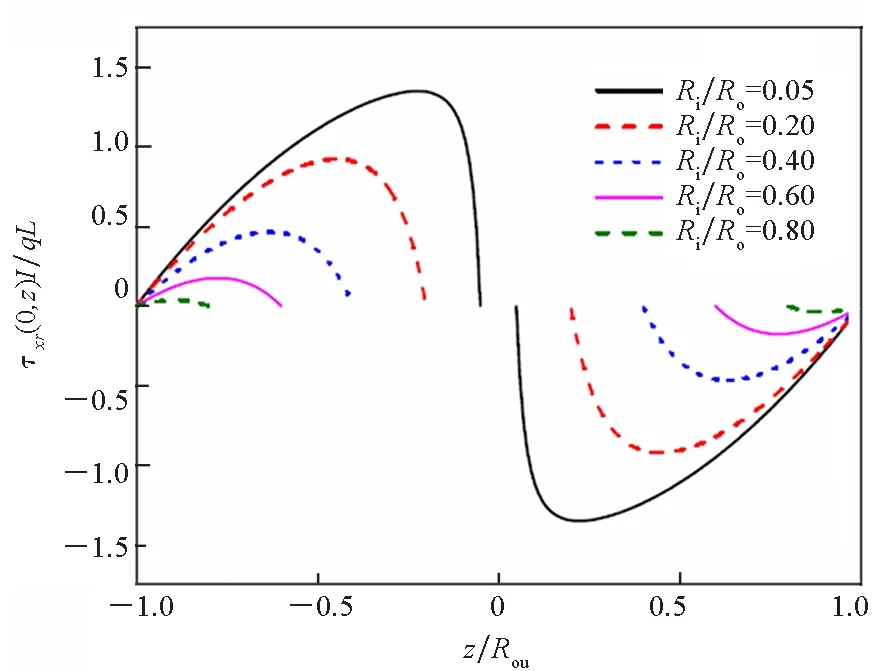
图7 不同内外半径比悬臂圆柱管剪应力τxrA/qL的分布情况( L/Ro=5,x=y=0 )Fig.7 Distribution of shear stress of the cantilever hollow cylindrical tube( L/Ro=5,x=y=0)
4 结论
1)本文所推导方法为考虑弹性基的圆柱管弯曲问题精确解求解提供了一个新的途径。所提方法充分地考虑了剪切变形和转动惯量的影响。通过与已有文献和经典梁理论的计算结果对比,证明所提理论具备足够精度。
2)通过对圆柱管截面应力分布的研究,验证了所提模型自动满足内外表面剪应力τxr为零的边界条件。
3)由于受剪切变形的影响,圆柱管横截面上正应力与横向坐标变量呈非线性分布的关系,且这一现象在长径比较小和厚径比较大时更为明显。
4)剪应力τxz在远离中间平面时,应力值逐渐减小,并在靠近顶部和底部位置逐渐消失为零,应力值在中间平面的内表面达到最大,即中间面内表面位置容易发生剪切破坏。
