全隐LU-SGS算法在高超声速热化学非平衡流刚性问题中的应用*
2022-04-06王君媛
蒋 浩,柳 军,王君媛,黄 伟,杜 洋
(国防科技大学 空天科学学院, 湖南 长沙 410073)
下一代天地往返空天飞行器具有高马赫数、宽速域的特点,穿越空域从对流层、平流层变化到临近空间,更为复杂的飞行任务剖面给飞行器气动、结构和热防护系统设计等带来巨大挑战,在设计中必须考虑高温气体效应的影响[1]。当飞行器高速再入时,在头部脱体激波及边界层的强黏性干扰作用下,空气被加热至数千度高温,其中的氧气和氮气组分发生振动激发、离解甚至电离,成为由分子、原子、离子和电子组成的混合气体,且当流动特征时间与能量松弛、组分化学反应特征时间相互比拟时,流动被称作热化学非平衡流。美国在早期航天飞机设计中依据完全气体假设,在试飞实验中出现了配平攻角高出设计值一倍多的气动异常现象[2]。
因此,在依靠计算流体力学(Computational Fluid Dynamics, CFD)工具进行高超声速飞行器气动预测时,常规的完全气体假设不再适用,必须采用考虑热化学非平衡的高温气体假设,但热化学非平衡计算存在严重的数值刚性问题,即数值计算失稳或收敛困难。其中,第一类是由源项带来的刚性,这是由于局部流场的流动特征时间可能与能量松弛、化学反应特征时间量级尺度存在极大差异,使得控制方程中相应源项的量级相差太大,进而在时间推进求解时出现收敛困难甚至发散的问题。第二类是由网格加密带来的刚性,热化学非平衡流动计算特别是热流计算对壁面网格加密要求极高,通常要求当地声速网格雷诺数小于10[3];另外,激波/边界层干扰等复杂流动要求在局部流场参数梯度较大的区域进行网格加密,这进一步加剧了网格刚性的问题。基于上述两种因素分析,热化学非平衡流程序相比完全气体程序,稳定性和鲁棒性较差,为满足稳定性限制,热化学非平衡流动计算库朗数 (Courant-Friedrichs-Lewy, CFL)一般取值较小,特别在采用显式时间推进格式时,该问题极为突出[4]。为此,在热化学非平衡流实际计算中一般选用稳定性较好的隐式格式,通过预处理方法以放宽线性方程组迭代求解对时间步长的限制。
美国从20世纪80年代开始热化学非平衡CFD研究,为了解决化学反应源项的刚性问题,Bussing 和Murman[5]提出将化学反应源项进行隐式处理,由于隐式项不需进行空间差分离散处理,只考虑本单元数据对本单元残差的贡献,故该算法被称作点隐式格式。在此基础上, Eberhardt和Imlay[6]提出了化学反应源项Jacobian矩阵的对角化形式,简化了化学反应源项的隐式处理。为进一步提高CFL数,有必要增加对流项的隐式处理,Yoon和Jameson[7]提出了LU-SGS(lower-upper symmetric Gauss-Seidel)算法,该算法通过正负分裂对流项Jacobian矩阵,将线性方程组左手项分解为三个子矩阵,因而避免了复杂矩阵求逆过程。LU-SGS算法最初被用于跨声速的流动求解,之后被推广到高超声速流动计算中,成为热化学非平衡流定常计算中最为通用的隐式时间推进算法。Chen和Wang[8]在完全气体LU-SGS算法基础上发展了BLU-SGS (block LU-SGS)算法,该算法在保证隐式系统对角特性的基础上,在每次更新中嵌入内迭代过程,通过内迭代过程中的上扫和下扫引入非对角块的贡献。另外,相比LU-SGS这类线性迭代求解算法,学者还研究了GMRES (generalized minimum residual) 等非线性迭代求解算法[9-10],进一步提高了高超声速流动计算效率。
尽管在完全气体计算中,Tysinger[11]、曹文斌[12]等研究发现,对黏性项隐式处理可提高计算效率,然而由于高温热化学非平衡流动控制方程包含多组分及多温度,相比完全气体其控制方程变量和方程数目增多,其中黏性项Jacobian矩阵推导过程复杂,国内外高温程序对黏性项的隐式处理则较少见诸报道[4,13-15]。另外,国内赵慧勇[16]在用于燃烧计算的化学非平衡流程序中植入了考虑黏性项隐式处理的LU-SGS算法,但未考虑热非平衡效应且未对其加速特性进行讨论。
本文基于结构网格有限差分法,总结提出热化学非平衡流动计算中强数值刚性带来的收敛困难问题;给出热化学非平衡流黏性项Jacobian矩阵的推导结果,并在时间推进算法中对该部分矩阵采取对角简化形式,实现对化学反应源项、对流项、黏性项的全隐处理,将完全气体条件下的FLU-SGS及BLU-SGS算法推广到热化学非平衡流动计算中;针对高超声速热化学非平衡二维圆柱实验和轴对称返回舱实验算例,对比算法改进前后的加速收敛特性。
1 热化学非平衡流控制方程
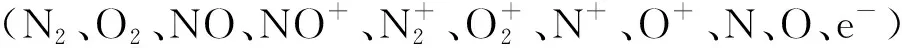
(1)
U=(ρ,ρi,ρu,ρv,ρet,ρev)T
(2)
其中:E和F是对流项;Ev和Fv是黏性项;W是源项;ρ是总密度;ρi分别为11个组元的密度;u和v是速度分量;et和ev分别为混合气体的单位质量总能和振动能。将上述控制方程进行坐标变换,得到计算坐标系下的形式:
(3)
2 热化学非平衡流全隐LU-SGS算法
2.1 黏性项隐式处理
热化学非平衡流原始LU-SGS算法[13-15]在隐式处理方面仅考虑化学反应源项和对流项,即:
(4)
其中,Δt是时间步长。本文在式(4)基础上,新增对黏性项的隐式处理:
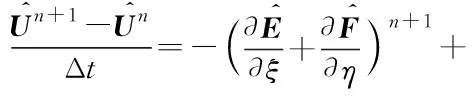
(5)
由于对流项仅是守恒变量的函数,将其进行线化处理,可利用时间方向上的泰勒展开:
(6)
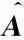
(7)
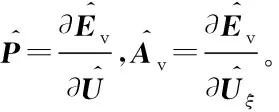
=Δt·RHS
(8)
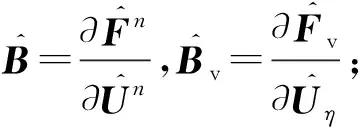
(9)
其由空间离散得到,对流项离散格式采用AUSMPW,黏性项离散格式采用二阶中心差分。
由于高超声速定常流动计算对时间精度要求不高,且黏性项Jacobian矩阵形式复杂,求逆需耗费大量计算时间,因此通常采用相应的矩阵谱半径进行对角近似处理,以保证左手项部分对角占优。经推导(推导过程见本文OSID拓展阅读资料),热化学非平衡流计算坐标系k方向上黏性项Jacobian矩阵的谱半径为:
(10)
其中,
Di是组元扩散系数,K、Kv分别是混合气体平动和振动热传导系数,Cv是定容比热比,Tv是振动温度,ev,i是分子组元的振动能,s=mol代表所有的分子组元,详细定义参见文献[20]。
2.2 FLU-SGS算法
参考原始LU-SGS 算法,对式(8)进行近似LU分解,再使用一次对称Gauss-Seidel迭代,则时间推进可化为三个步骤:
1)向前扫描:
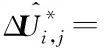
(11)
2)向后扫描:
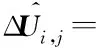
(12)
3)守恒量更新:
(13)
此外,本文采用当地时间步方法计算每个网格点的Δt。
2.3 BLU-SGS算法
与LU-SGS算法不同的是,BLU-SGS算法在每次守恒量更新步内还包含了smax次松弛迭代。若smax=1,则退化到LU-SGS算法;对于不同的算例,内迭代数smax存在着不同的最优值[11]。第s次内迭代表达式如下:
1)向前扫描:
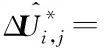
(14)
2)向后扫描:
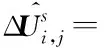
(15)
(16)
3 数值结果
3.1 二维圆柱绕流
3.1.1 来流条件及计算结果
本算例基于高焓激波风洞HEG中开展的准二维圆柱绕流实验[21],风洞来流焓值21.7 MJ/kg,计算采用的气体模型是11组元空气,壁面条件为等温全催化壁面,圆柱半径R为45 mm,详细风洞来流条件和计算条件见表1。网格分布最终采用249×39,经过网敏感性分析后,最终壁面第一层距离采用3×10-7m,当地声速网格雷诺数达到6.7,满足热流计算网格收敛性条件[3]。
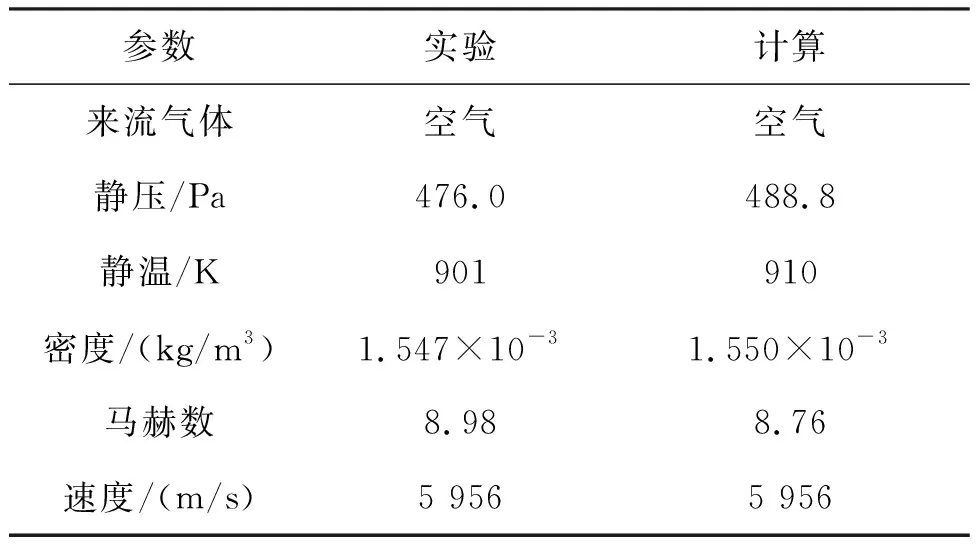
表1 二维圆柱算例来流条件
图1为圆柱绕流无量纲压力云图,结果显示本文程序能较好地捕捉到激波位置,流场中各物理量计算结果比较合理。图2是圆柱壁面热流Qw计算结果与实验结果对比,可以看出壁面热流计算值与实验值符合良好,验证了本文数值方法的正确性。
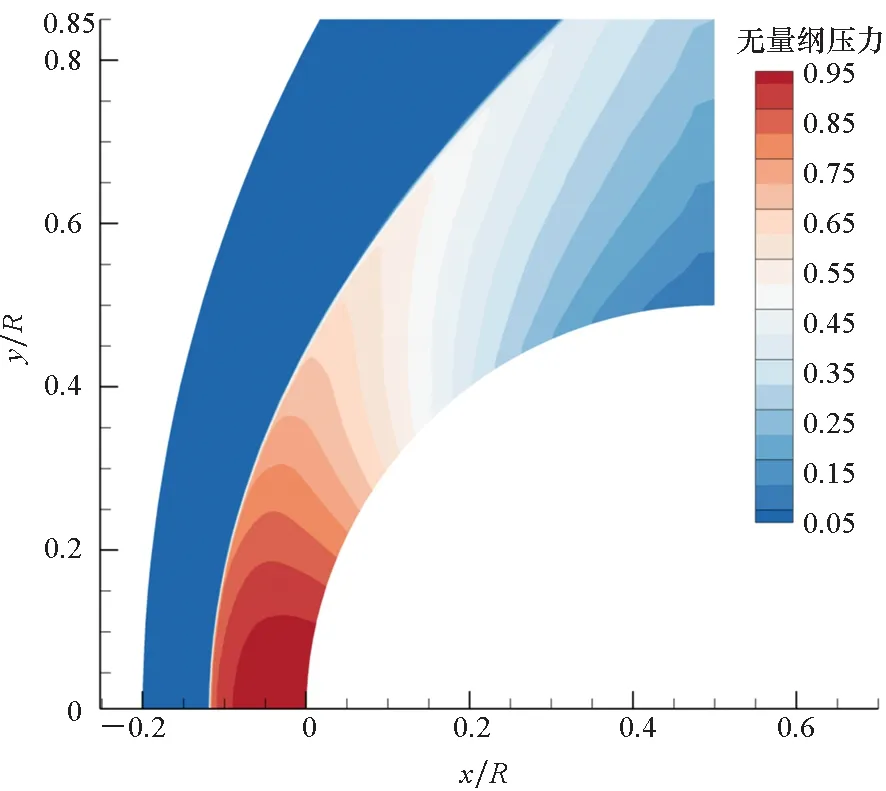
图1 圆柱绕流无量纲压力云图Fig.1 Dimensionless pressure contour for cylinder case
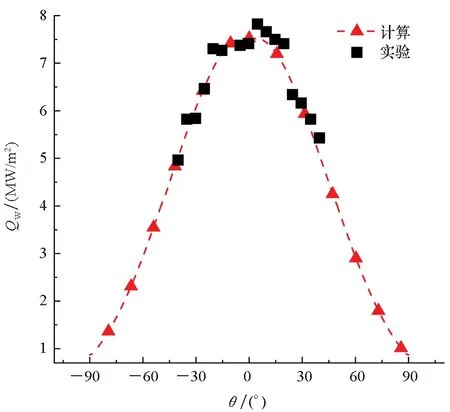
图2 圆柱壁面热流对比结果Fig.2 Comparison of the heat flux of cylinder wall
3.1.2 三类LU-SGS算法收敛速率对比
高超声速计算普遍采用来流条件作为初场,计算流场普遍经历以下过程:从流动在壁面附近滞止、形成脱体激波或分流区,直至收敛呈现为稳定的流场结构,其中流场基本结构的建立是整个计算过程中数值刚性最强的步骤。因此,在计算初期只能采用较低的CFL数以避免发散,待激波、边界层、分离等流动特征稳定建立后,才能逐步增大CFL数。在此,首先给出最大CFL数的定义:在该类格式下密度残差Δρ能收敛到机器误差(10-12)的CFL数的最大值。为比较三类算法在计算初期所能采用的最大CFL数,在数值实验中采用恒定CFL数进行计算。
图3为针对圆柱算例开展的关于三种LU-SGS算法收敛速率的数值实验结果。结果发现,三类LU-SGS方法的最大CFL数不同,采用原始LU-SGS算法,最大的CFL数取值约为0.01,而FLU-SGS算法的最大CFL数为10量级,BLU-SGS的最大CFL数可取到100量级,达到机器误差的迭代步约为FLU-SGS的73.4%。
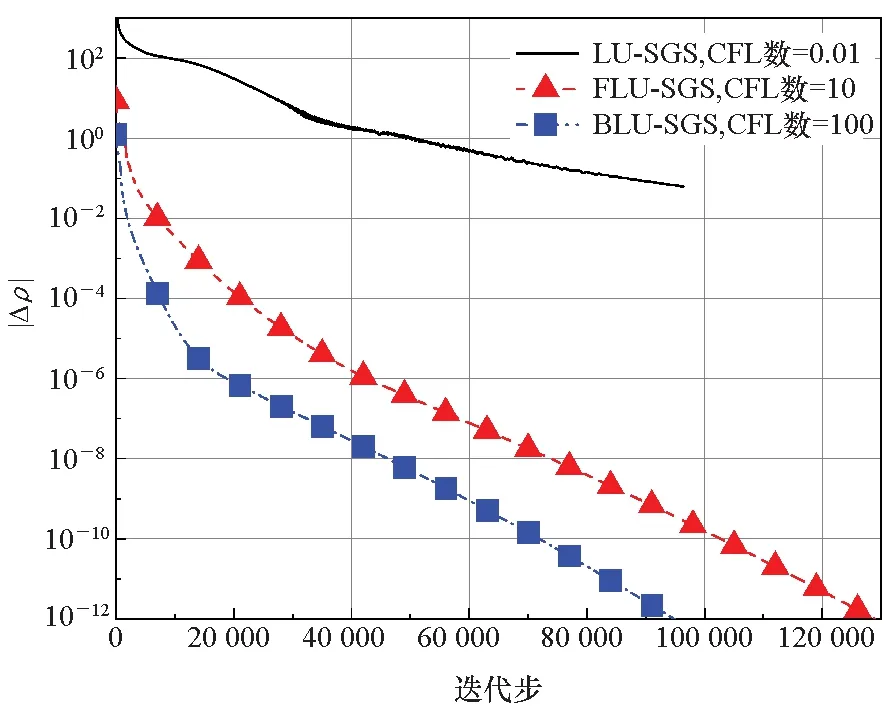
图3 圆柱算例三种LU-SGS算法收敛速率对比Fig.3 Comparison of the convergence rate between three LU-SGS algorithms for cylinder case
因此,增加黏性项隐式处理的FLU-SGS和BLU-SGS算法由于在计算中考虑了黏性干扰的流场信息,故能快速建立边界层。两类改进算法在20 000步前的收敛速率较大,而在此之后由于流动结构基本不变,收敛速率出现拐点,密度残差的收敛曲线近似呈线性,直至收敛到机器误差。另外,在近期文献[14]报道中,也对本节同样算例采用LU-SGS算法进行了热化学平衡流场计算,其CFL数取值为5,可见本文改进算法对提升收敛速率有较大优势。
3.1.3 CFL数对FLU-SGS算法收敛的影响
图4 对比了CFL数为10、100和1 000下采用FLU-SGS算法的收敛速率。结果表明,随着CFL数取大,前期收敛速率加快。尽管采用全隐算法后,初始CFL数能够取到1 000,但当残差降低到10-8后呈现周期振荡现象;当CFL数进一步取到10后,该种振荡现象能够消除,并能降低到机器误差。另外,虽然在大CFL数条件下的收敛后期,密度残差会出现周期振荡,但当其降低到10-6以下后,流动结构和壁面参数的实际变化很小,可近似认为收敛。
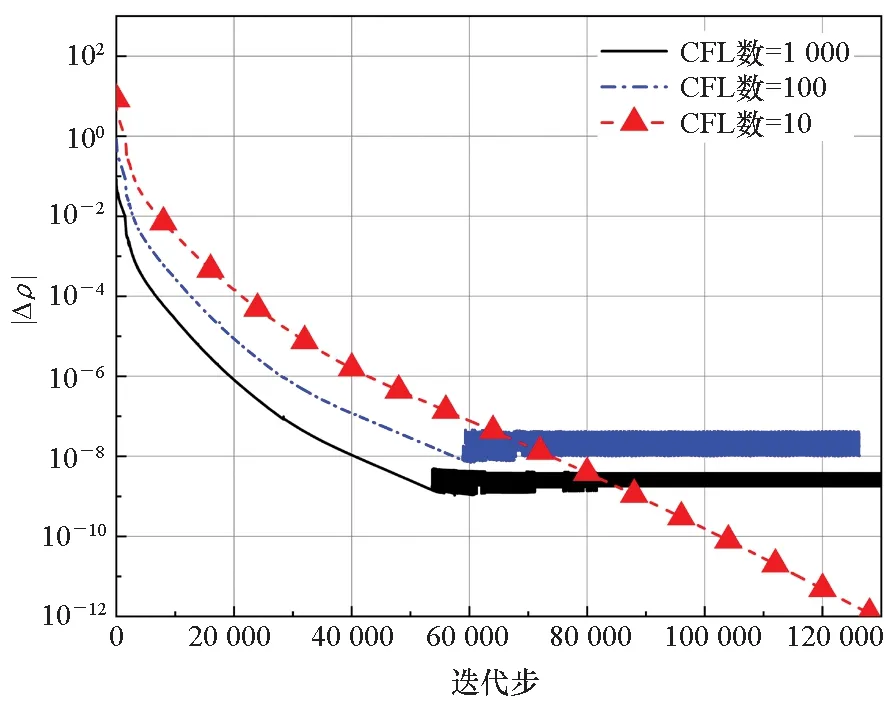
图4 圆柱算例中CFL数对FLU-SGS收敛速率的影响Fig.4 Effect of CFL number on the convergence rate of FLU-SGS for cylinder case
3.1.4 内迭代数对BLU-SGS算法收敛的影响
图5是内迭代数smax对BLU-SGS收敛速率的影响,可以看出在大CFL数条件下,增加smax抑制了计算后期的残差振荡,增加了收敛的稳定性。虽然smax越大,密度残差随迭代步的收敛速度加快,但是从计算机时角度看,增加smax耗时更多。
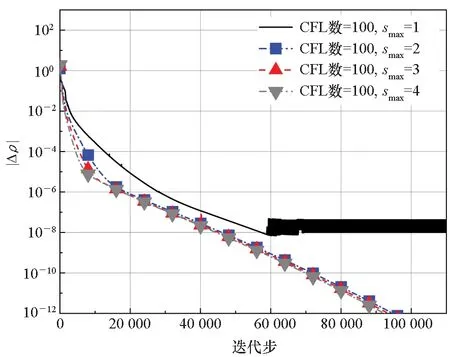
(a) 密度残差随迭代步的变化(a) Variation of density residual with iteration number
3.2 轴对称返回舱绕流
3.2.1 来流条件及计算结果
本算例基于Hollis在HYPULSE膨胀管风洞对MP-1返回舱实验模型的测量结果[22]。采用本文程序对该实验进行复现,实验模型是返回舱-支杆的构型,其中,支杆为固定装置,返回舱半径R=0.025 4 m。由于模型是轴对称构型,图6仅展示xy截面,其网格分布为208×119。来流条件为:马赫数Ma=7.93,速度U∞=5.162 km/s;压强P∞=1 824 Pa;平动温度T∞=1 113 K;振动温度Tv∞=1 113 K;来流雷诺数为668 000;来流组元为空气(N2和O2质量分数分别为79%和21%),壁面采用等温、无滑移、非催化壁条件,壁面温度为300 K。
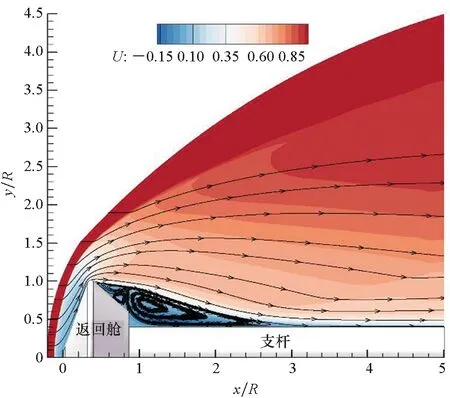
图6 返回舱算例无量纲x方向速度云图 Fig.6 Dimensionless x-velocity contour for re-entry capsule case
图6显示了返回舱绕流的无量纲速度云图,高速气流撞击返回舱前端产生脱体激波,波后形成强烈的压缩,前体部分是附着流动,流动在返回舱肩点之后发生了分离,并在尾部区域和支杆之间形成大型分离区,分离区内部有两对涡对,流动进而在支杆上再附,形成再附激波,支杆下游保持边界层附着流动。
3.2.2 三类LU-SGS算法收敛速率对比
图7对比了三类LU-SGS方法的收敛速率。由于返回舱绕流比圆柱绕流的流场结构更为复杂,在原始LU-SGS算法下的初始计算中,最大CFL数仅能取到10-4量级,因而收敛过程极为缓慢。采用FLU-SGS算法能将最大CFL数大幅提升到1的量级,但是后期收敛速率有所降低。BLU-SGS算法最大CFL数量级能达到10,能实现快速收敛,达到机器误差的迭代步仅为FLU-SGS的8.5%。
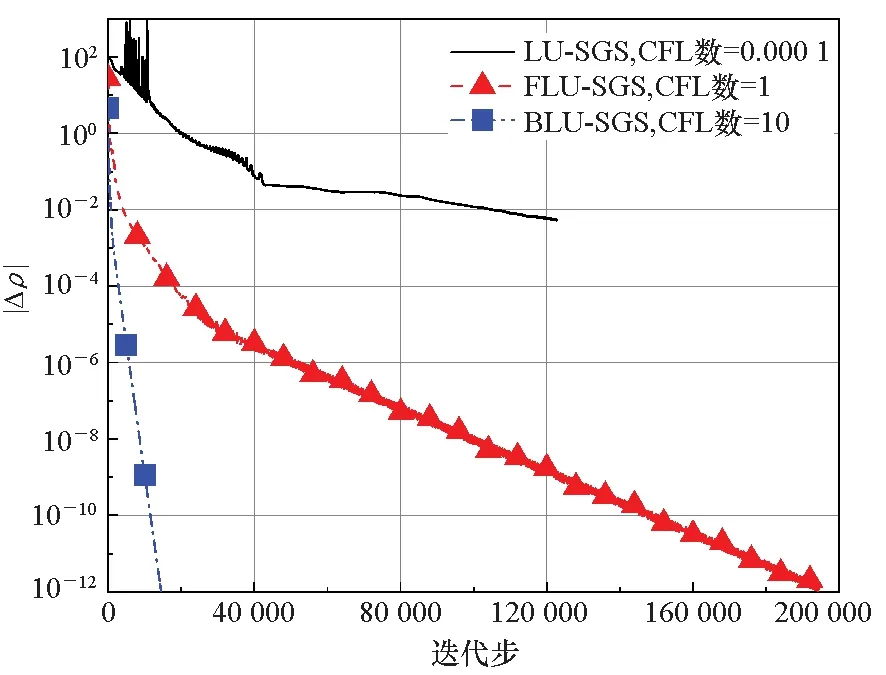
图7 返回舱算例三种LU-SGS算法收敛速率对比Fig.7 Comparison of the convergence rate between three LU-SGS algorithms for re-entry capsule case
3.2.3 CFL数对FLU-SGS算法收敛的影响
图8对比了CFL数为1、 10和100下采用FLU-SGS算法的收敛速率。结果表明,随着CFL数取大,前期收敛速率加快。同圆柱算例类似,在大CFL数下,残差降低到10-3后呈现周期振荡现象,当CFL数进一步取到1后,该种振荡现象能够消除,并能降低到机器误差。由于采用二阶格式,该类残差振荡现象与过激波参数在两个网格间跳动等因素相关。
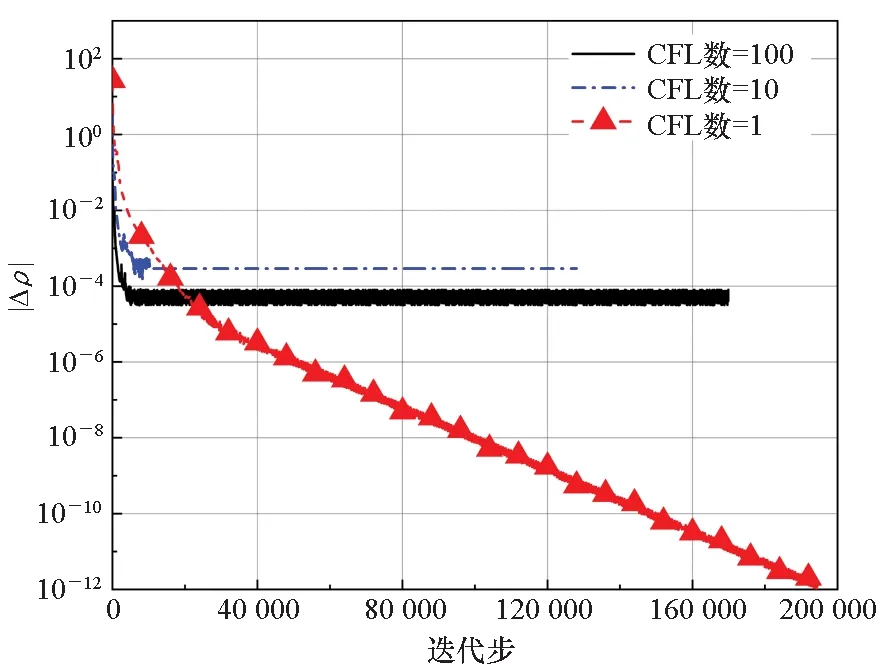
图8 返回舱算例CFL数对FLU-SGS收敛速率的影响Fig.8 Effect of CFL number on the convergence rate of FLU-SGS for re-entry capsule case
3.2.4 内迭代数对BLU-SGS算法收敛的影响
图9是内迭代数smax对BLU-SGS算法收敛速率的影响,可以看出在CFL数为10、smax=1时,BLU-SGS算法退化为FLU-SGS算法,内迭代数smax增加到3时才能抑制计算后期的残差振荡。
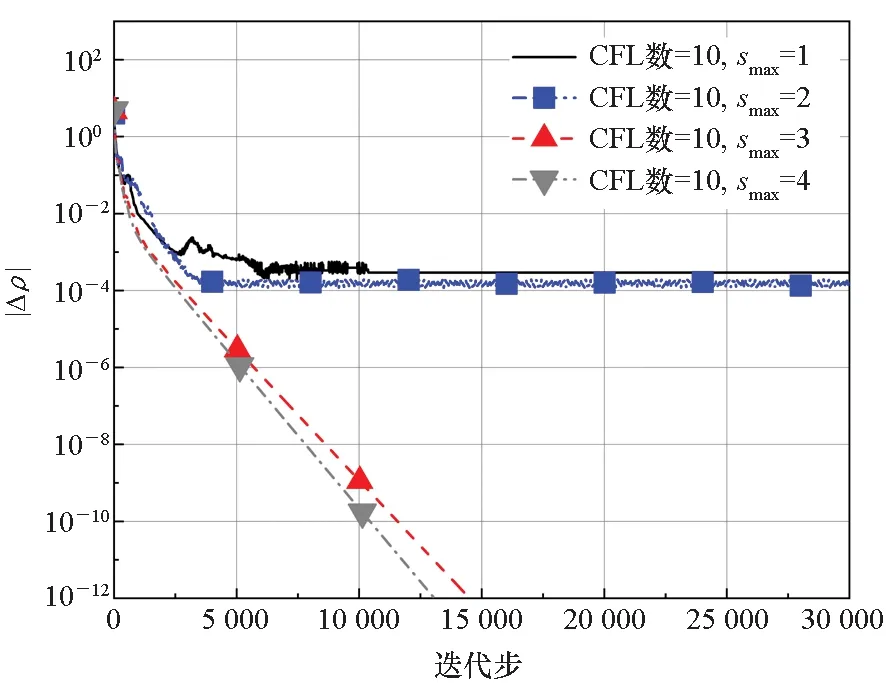
(a) 密度残差随迭代步的变化(a) Variation of density residual with iteration number
当内迭代数smax继续增加到4后,总密度残差随迭代步的收敛速度加快,计算机时有所增加。因此在实际复杂工程外形计算中,为兼顾计算稳定性和计算效率,选用BLU-SGS算法最佳,且在满足收敛到机器误差的要求下,内迭代数smax视情况可选取2至4,因为该参数取值过大对收敛性没有明显的增益,且浪费计算机时。
4 结论
1)在高温热化学非平衡流计算中,考虑黏性项隐式处理的两种全隐LU-SGS算法引入了跨越边界层的黏性影响,能够快速建立强黏性干扰初场,实现初始最大CFL数3~5个数量级的提升。
2)BLU-SGS算法通过增加内迭代数能提升计算稳定性,在高超声速热化学非平衡计算中准确性高、可靠性强、收敛速率快,适合复杂流场计算。
3)随着CFL数升高,计算稳定性有所降低,残差曲线表现小范围周期振荡,该现象与时间推进格式、对流格式、网格分布、流场非定常特性等因素相关,要进一步抑制该现象,需从构造适用于热化学非平衡流动的数值格式、提高数值格式精度和提升网格质量入手。
致谢
中国空气动力研究与发展中心赵慧勇研究员在公式推导方面提供了帮助和指导,谨致谢意!
