自动化集装箱码头岸边集装箱起重机与自动导引车协同调度研究

吴晓晓 吴敬兵

武汉理工大学 武汉 430070

0 引言

自动化设备和人工智能算法的普及极大地提高了集装箱港口码头的作业效率。港口的运作效率是船舶公司选择挂靠的重要因素，高效运作的港口可以缩短船舶的在港时间，降低码头作业成本。自动化港口的泊位、水平装卸设备和水平运输设备等港口资源设备因价格昂贵，无法大规模购买和建造，故需对其进行合理调度。水平装卸系统主要是指岸边桥式起重机（以下简称岸桥）和场堆桥式起重机（以下简称场桥），岸桥是自动化码头作业中装卸的重要组成部分，针对停靠在港口船舶上的集装箱进行装卸。水平运输设备自动导引车( Automated Guided Vehicle，AGV）是连接自动化码头装卸设备的枢纽，岸桥和AGV的调度影响着码头整体的运作效率。

岸桥的调度问题主要针对其作业顺序进行优化，研究表明：岸桥的调度问题为NP-难问题，精确求解这类问题往往较困难[1]。Dong L等[2]研究了岸桥调度对于码头作业效率的影响，建立了一个混合整数规划模型，同时设计了遗传算法和2种基于分段编码技术的改进算法求解。梁承姬等[3]重点研究了岸桥调度和分配问题，以船舶在港时间最小为目标，建立了混合整数规划模型，并设计遗传算法进行求解。Dominik K等[4]为了精确研究岸桥的调度问题，以最小化的最大岸桥作业完工时间为目标，提出了一种解决岸桥调度的动态编程的方法，用动态规划算法求解。水平运输系统作业效率的提高能提升装卸设备的作业效率，进而提高整个自动化码头的作业效率。但是过多地投入AGV会造成AGV之间的互相等待，导致运输区域的拥堵，故在满足任务时间的要求下应尽量减少AGV使用数量。Jin J等[5]采用调度的优先级次序方法解决自动化港口码头AGV的调度问题；郭保青等[6]使用蚁群算法求解仓库中多AGV调度的路径问题。

自动化码头作业系统实际运作过程中并不是靠单一的设备调度，而是需要各系统间的协同调度。关于子系统之间的调度, 目前研究的重点主要集中岸桥和AGV小车之间的联合调度、AGV和场桥之间的联合调度。He J等[7]研究了岸桥、AGV和场桥的协同调度问题，以最小化场桥成本为目标，建立了混合整数规划的模型，用分支定界法进行求解。Zhao J等[8]研究了岸桥和AGV的综合调度问题，同时以最小化集装箱船卸载任务完成时间开发了粒子群的算法求解。自动化码头的调度是一个复杂的整体系统，对于单一的目标优化对提高自动化码头作业效率并不显著，也不符合实际情况。然而，上述文献大多集中于以单一目标，研究2个子系统之间的协同调度问题，并不能反映真实港口调度过程中对于多目标优化的需求。本文针对于自动化港口的双岸桥小车和AGV的2个子系统间的调度进行研究，以最小化最大完成时间和最小化AGV行驶距离为目标，建立混合整数规划模型，同时用改进的遗传算法进行求解。

1 问题描述

按照自动化码头功能进行分类，其作业区可分为泊位区、岸桥作业区、水平运输区、堆场作业区等区域。自动化港口的布局如图1所示。在码头调度过程中，任何一个最优的作业流程往往会因另一个流程未能与其对接而无法顺利实施，这就要求对码头作业进行合理的规划调度。

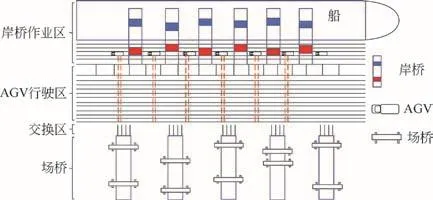
图1 自动化港口布局图

自动化码头的功能区域并不是完全独立而是相互分工合作的。一般情况下，自动化港口在抵达港口前会把船舶的船型、到港时间、装载集装箱量和船舶预计离港时间等信息上报给码头的调度者，工作人员依据这些信息和设备状态制定出相应的泊位和岸桥计划。船舶停靠港口后，集装箱码头会配置一定数量的岸桥对船舶进行装卸作业。岸桥的调度主要是通过制定岸桥作业计划来衔接岸边和堆场作业的工作，以减少岸边和箱区的作业冲突, 从而进一步提高码头的整体运作效率。双小车岸桥主要由主小车和后小车构成，其作业流程为：在主小车接收到指令后，将船舶贝位上的集装箱拾起后放置在岸桥的中转平台上。双小车岸桥的中转平台可同时容纳2个40 ft或4个20 ft的集装箱。然后，双小车岸桥的门架小车从中转平台上将集装箱拾起后放置在岸桥下方等待的AGV上。双岸桥小车的模型如图2所示。相较于传统集装箱装卸作业流程，自动化码头装卸作业的特点是使用了AGV来替代传统拖车作业。AGV按照预先设定的轨道将集装箱从岸桥运输到场桥进行堆垛。另外，双小车岸桥中转平台能将集装箱暂存，很好地解决了岸桥和AGV之间的耦合问题，尽可能地减少AGV小车等待岸桥的时间，实现高效的自动化港口装卸作业。

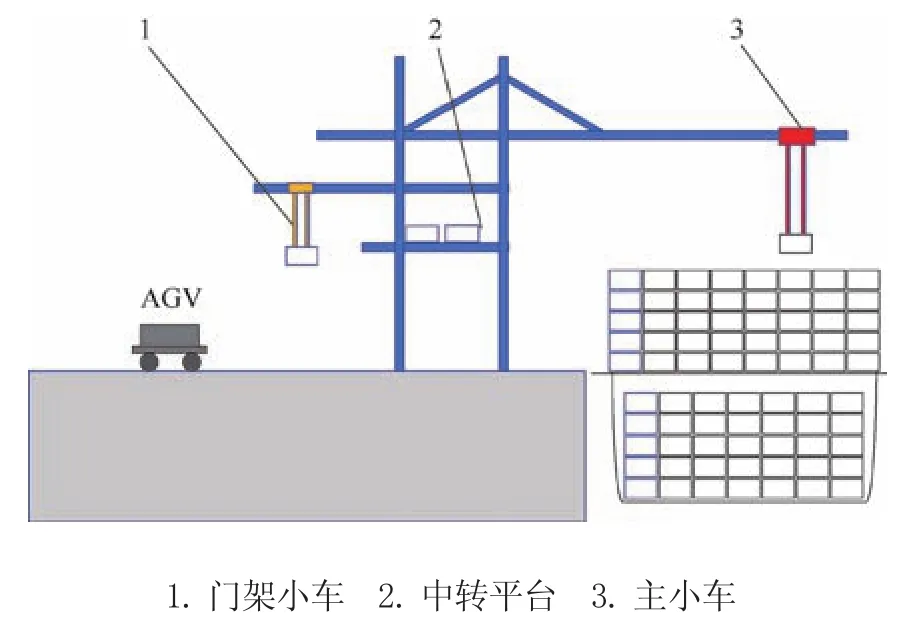
图2 双小车岸桥示意图

显而易见，自动化港口的岸桥调度和AGV调度计划共同影响着整个码头。岸桥AGV协同调度需要充分考虑岸桥和AGV之间的相互关联和相互影响关系，使岸桥和AGV相互衔接顺利。本文重点研究双小车岸桥与AGV的协同调度问题，通过对主小车和门架小车的调度实现双小车岸桥与AGV调度优化，使用遗传算法求解，给出最优的双小车岸桥和AGV调度方案，并对算例进行分析。

2 模型建立

2.1 模型假设

模型假设条件：1）岸桥QC和双自动堆垛起重机ASC一次只能装载或卸载1个集装箱；2）AGV小车一次只能运输1个集装箱；3）不考虑岸桥QC之间的干扰冲突；4）AGV小车匀速行驶；5）场桥ASC不能跨堆场作业。

2.2 目标函数

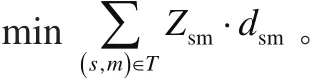
2.3 集合与参数

N为进口集装箱集合，n∈N；L为出口集装箱集合，l∈L；I为所有任务（集装箱）的集合，I＝N∪L，i，i′∈I，其中0和f为虚拟起始任务和虚拟结束任务，虚拟任务的作业时间都为0；Q为QC集合，q∈Q；A为AGV集合，a，a′∈A；B为ASC集合，b∈B；K为所有设备的集合，K＝Q∪A∪B；M为一个很大的正整数；J为路径网络中的所有节点集合，s、m、s′、m′∈J；G为节点之间的有向线段；v为AGV的速度；C为所有集装箱的最大完工时间；dms为节点s与节点m之间的距离；SQ为岸桥Q的中转平台可容纳的集装箱数量。

2.4 变量

1）0-1变量

在设备k上，Xkii′： Xkii′＝1，集装箱i先于i′处理，Xkii′＝0，否则；Yki：Yki＝1，设备k处理集装箱i，Yki＝1，否则；Zsm：Zsm＝1，通过节点s与节点m之间的连接路径，Zsm＝0，否则；Pas：Pas＝1，AGV a经过节点s，Pas＝0，否则。

2)非0-1变量

tsqi为QC q开始处理集装箱i的时间；teqi为QC q处理集装箱i的时间，对于进口箱表示QC q将集装箱从船舶送到中转平台再运送到AGV上的时间，对于出口箱表示QC q将集装箱从AGV转移到中转平台再运送到船舶上的时间；tsai为AGV a开始处理集装箱i的时间，对于进口箱表示AGV到达QC与AGV转移点的时间，对于出口箱表示AGV到达ASC与AGV转移点的时间；teai为AGV a处理集装箱i的时间，对于进口箱表示AGV将集装箱运送至ASC与AGV转移点的时间，对于出口箱表示AGV将集装箱运送至QC与AGV转移点的时间；tsbi为ASC b开始处理集装箱i的时间；tebi为ASC b处理集装箱i的时间，对于进口箱表示ASC b将集装箱从转移点运送到堆场位置的时间，对于出口箱表示ASC b将集装箱从堆场位置运送到AGV上的时间；tae，sm为AGV a进入节点s与节点m之间的连接路径的时间；tao，sm为AGV a离开节点s与节点m之间的连接路径的时间。

2.5 约束条件

1）上层模型

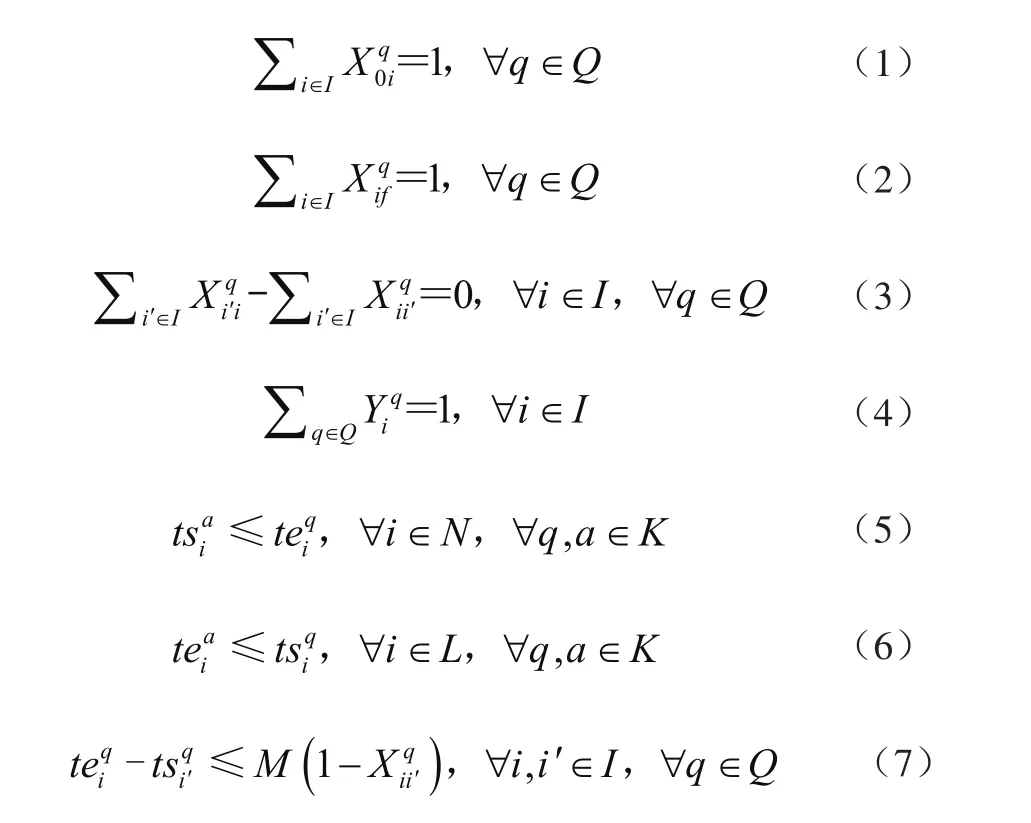
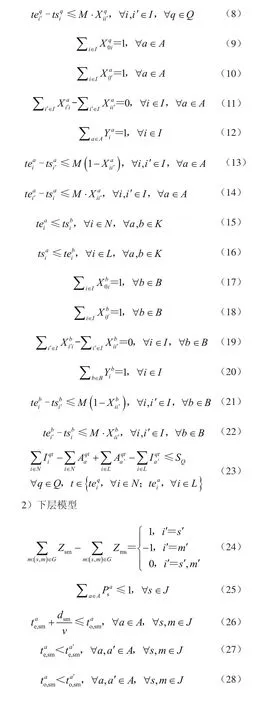
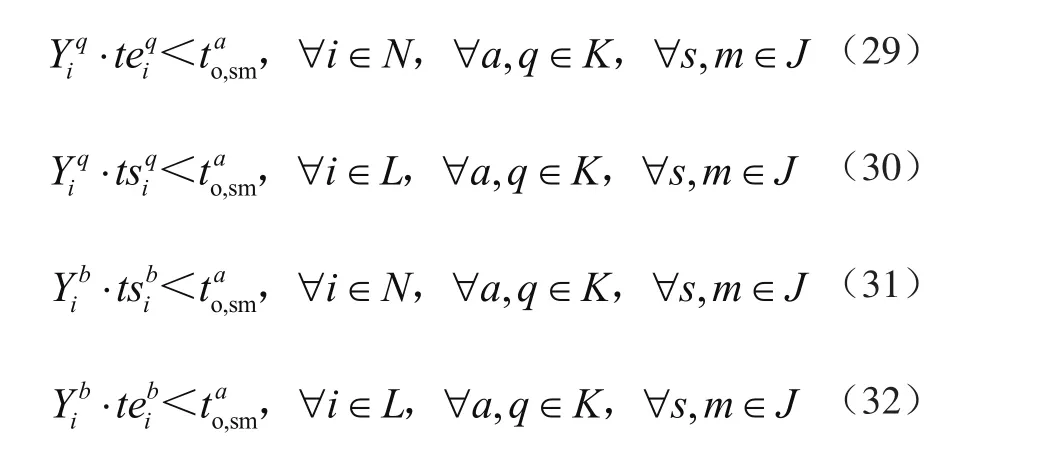
由以上公式可知，式（1）、式（2）保证每台QC的初始任务为虚拟任务0，结束任务为虚拟任务f；式（3）保证QC处理每个集装箱的作业顺序；式（4）保证每个集装箱只能被1台QC处理；式（5）AGV需提前到达转移点等待QC；式（7）、式（8）保证在同一台QC上前一个集装箱的完成作业时间早于下一个集装箱的开始作业时间；式（9）、式(10)保证每台AGV的初始任务为虚拟任务0，结束任务为虚拟任务f；式(11) 保证AGV处理每个集装箱的作业顺序；式(12)保证每个集装箱只能被1台AGV处理；式(13)、式(14)保证同一台AGV运输的2个集装箱的先后时间顺序；式(15)、式(16)需提前到达转移点等待ASC；式(17)、式 (18)保证每台ASC的初始任务为虚拟任务0，结束任务为虚拟任务f；式(19)保证ASC处理每个集装箱的作业顺序；式(20)保证每个集装箱只能被1台ASC处理；式(21)、式（22）保证同一台ASC处理2个集装箱的先后时间顺序；式（23）表示每个中转平台上的集装箱数量不超最大容量限制2；式(24)路径选择约束；式(25)节点约束，同一节点只能通过1台AGV；式(26)AGV a进入和离开路径的时间关系；式(27)连续2台AGV进入同一路径的时间约束；式(28)连续2台AGV离开同一路径的时间约束；式(29)、式(30)QC与AGV转移集装箱的时间小于AGV离开路径的时间；式(31) 、式(32)ASC与AGV转移集装箱的时间小于AGV离开路径的时间。

3 遗传算法

遗传算法的前提条件为：1）岸桥处理集装箱的顺序已知；2）岸桥的优先级高于小车，在小车的分配前提条件下可让小车等待岸桥，应尽量避免岸桥等待小车；3）在此过程中，获得每AGV任务的等待时间和空载时间。

上述岸桥调度和AGV调度属于典型的NP-Hard问题，对于这种相对较大的实例，数学方法无法在合理的计算时间内为大规模集成调度问题找到最佳解决方案。大量研究表明遗传算法可以解决集装箱码头各种调度计划问题，如岸桥调度、泊位调度、场桥起重机调度和AGV的调度等。遗传算法是一种基于自然选择和自然遗传学的随机搜索技术，是一种用于寻找优化问题解决方案的著名元启发式算法。GA的整体框架如图3所示。本文使用Matlab 2020b，利用分别使用遗传算法和禁忌搜索遗传算法求解模型的解。

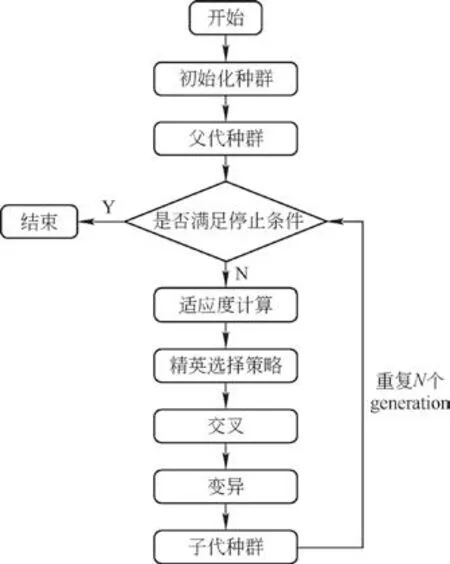
图3 遗传算法流程图

3.1 染色体的编码

采用整数编码方法随机生成一条染色体，每条染色体代表模型的一个解。集装箱的编号就是构成染色体的基因值，集装箱在染色体的位置即为集装箱任务的优先顺序。表1为染色体编码的分布情况，假设共有2个岸桥QC、10个集装箱任务、5个AGV小车来运输集装箱。

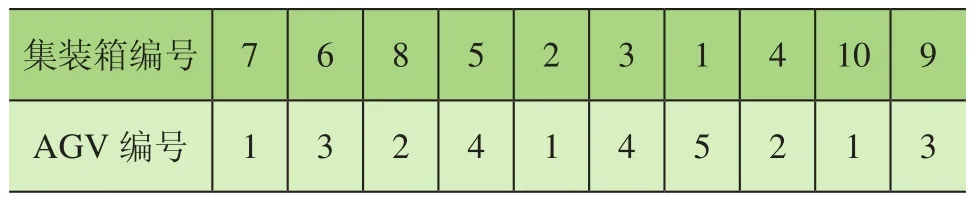
表1 染色体编码分布示意表

3.2 初始种群和适应度函数

由于遗传算法的搜索空间较大，在实际过程中常采用随机生成种群的方式来增大种群个体的多样性，尽可能增加遗传算法的全局搜索能力，避免陷入解的局部最优，以维持种群的多样性。本文通过随机生成n个染色体的全排列，就构成了初始种群。

在遗传算法中，染色体的适应度值越高，则其被留存在子代的概率就越高。对于已经建立的数学模型问题，通常直接采用模型的目标函数值作为适应度函数。本文采用适应度函数值取目标函数的倒数，F＝1/f，即最小化岸桥最大完工时间的倒数。

3.3 选择运算

在选择算子时，采取的策略是轮盘赌和精英选择策略保留的方式。个体被选中的概率与适应度值有关，遗传染色体个体的适应度值越大，则其被选中的概率就越大。遗传算法的选择概率设置为0.9，使用轮盘赌选择方式选择产生的种群。选择运算要求适应度高的个体将会有更多的机会遗传到下一代群体中选择策略。采用轮盘赌方法进行选择的策略是：在选择过程中，采用比较经典的精英选择+轮盘赌的选择方式。使用轮盘赌的方式选择2个父代中的个体进行选择操作，具体步骤为：1）选择2个父代中的个体；2）对2个父代的个体进行n次交叉操作；3）计算这2个子代的适应度值，并记为i1、i2；4）选择max(i2,i2)最大值的一组结果（用L表示）；5）与父代的2个个体比较，比较父代适应度值与L的大小；6）选择大的作为新一代的2个个体，其目的是为了产生更好的后代。

轮盘赌的具体策略是先计算出群体中所有个体适应度的总和，再计算出每个个体的相对适应度大小，即是每个个体被遗传到下一代群体中的概率。每个概率值组成一个区域，全部概率值之和为1。最后再产生一个0～1之间的随机数，依据该随机数出现在上述哪一个概率区域内来确定各个个体被选中的次数。

3.4 交叉运算

交叉运算的目的是使遗传算法中产生新的个体过程。使用交叉概率（交叉率Pc）相互交换2个个体之间的部分染色体，本文采用双切点交叉法。从种群中选择染色体P1、P2为父代，新的个体C1、C2 为子代。具体步骤为：1）选2个切点；2）交换父代切点内部分；3）将未换部分按映射关系恢复合法性；4）调整局部优先级，过程如表2所示。

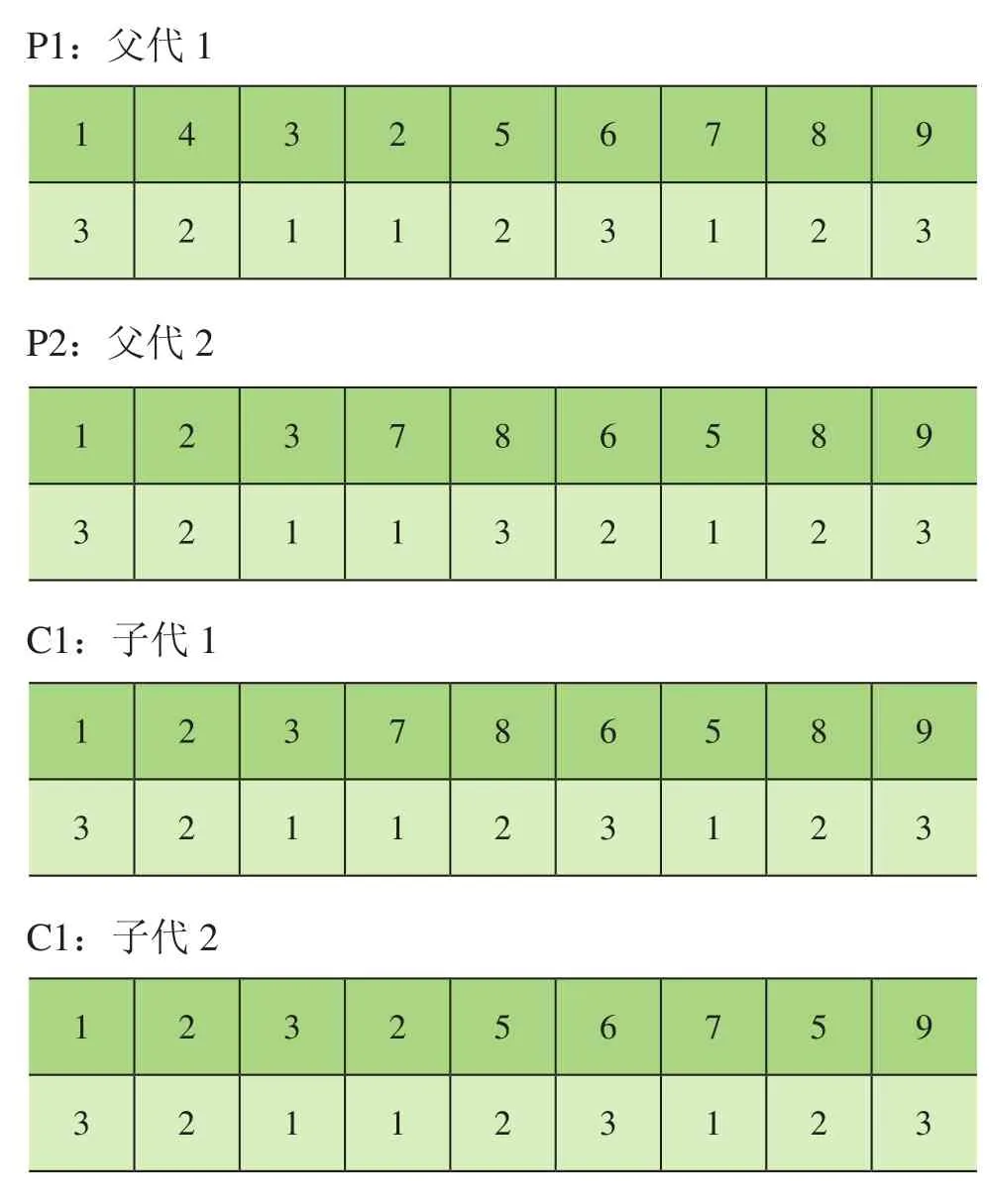
表2 调整局部优先级过程的染色体示例表

3.5 变异运算

遗传算法的变异运算操作是对染色体个体的某一基因或某些基因按照变异率Pm进行改变。其具体操作为选择一个父代染色体P1，然后随机交换染色体上。随机地在染色体上选取2个位置，交换2个基因的序号，编码合法，则生成子代 C1，完成染色体的变异操作。

4 数值试验

为了评估模型和算法的有效性，本文针对分别针对小规模问题和大规模问题进行了验证。评价的指标为最佳适应度值（OFV）和求解时间，为了避免算法的随机性导致的误差，每个实验重复进行10次。遗传算法的参数设置不同，对于算法的求解结果不同，本文所设置的遗传算法的参数为：最大迭代数为200、交叉概率0.85、变异概率0.2、种群规模为100个。

4.1 参数设置

以某港实际运行情况为例，集装箱的数量从4到70不等。假设共有2～3台岸桥、4～12辆AGV。岸桥QC作业将集装箱从船舶卸载到AGV或将集装箱从AGV装载到船舶上的时间服从均匀分布U(30,180)s；ASC场堆起重机的作业时间服从均匀分布U(60,140)s；AGV行驶路网的长度为200 m，宽度为150 m；道路为单向，同时道路的宽度忽略不计；场堆的长度为200 m，宽度为200 m；AGV行驶速度为5 m/s，双小车岸桥中转平台的容量为2。

4.2 实验结果

1）小规模实验结果

如表3所示，通过2种方法的对比，禁忌搜索遗传算法可获得近似最优解。与遗传算法对比，禁忌搜索遗传算法能很好地解决遗传算法因种群多样性降低导致的早熟特征，从而更好地寻求最优解，避免陷入局部最优解。依据表中数据，GA的计算时间57.3～397.1 s波动剧烈，而TSGA的计算时间116.3～587.3 s有波动，这表明使用TSGA相比GA在任务量增加时相对平稳，由此判断在大任务量时TSGA表现要优于GA，两者算法的差值能接受。

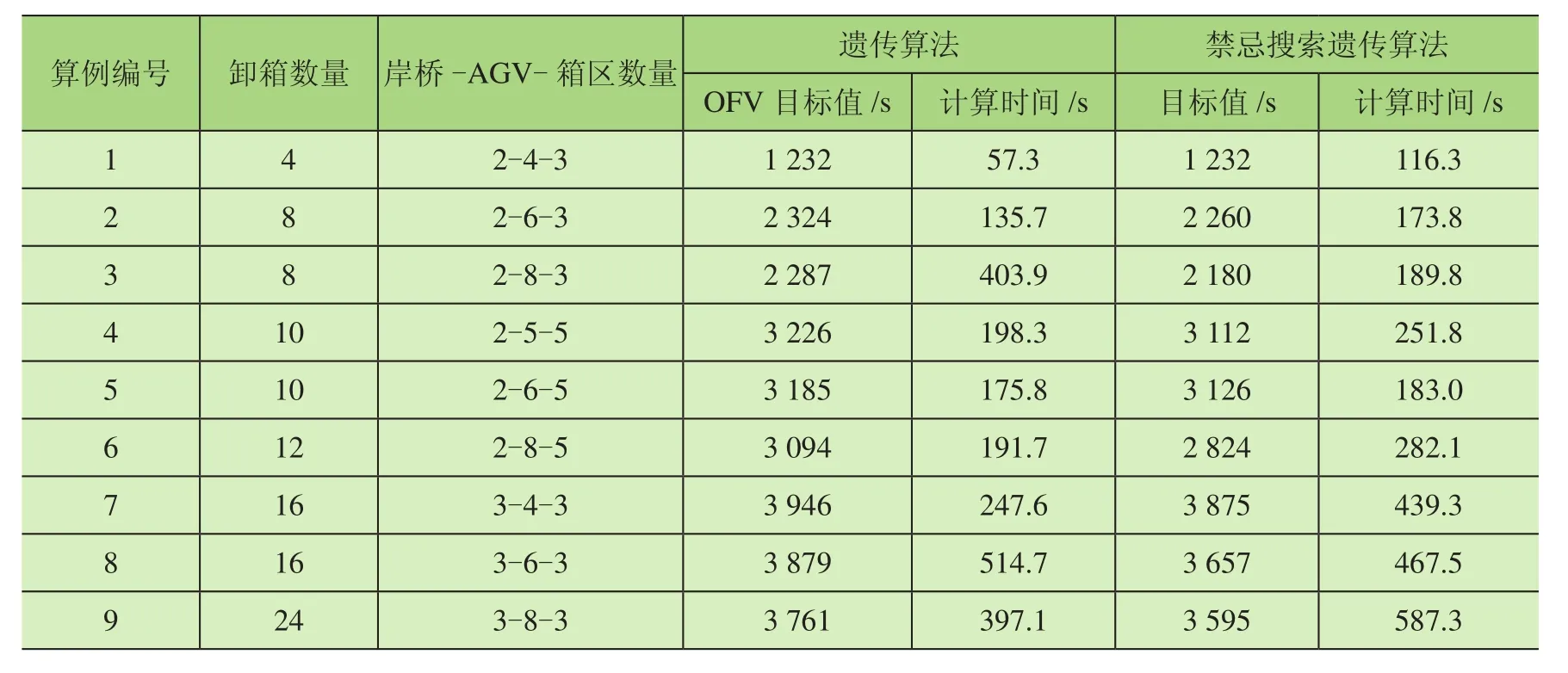
表3 禁忌搜索遗传算法和遗传算法对比(小规模)

随着集装箱任务数量的增加，2种算法的运行时间都逐渐变长，最优化求解差距亦较大，其中TSGA的最优化结果小于GA，证明了TSGA算法在解决此类问题的有效性。从算例4和算例5可以看出，集装箱的任务数量一定时候，AGV的数量越多效率越高。从算例8和算例9可以看出，尽管任务数量增加，但增加AGV的数量也能显著降低OFV值，这表明当增加任务的数量时，增加AGV小车的数量可以减少集装箱的最大化完工时间，从而提高码头的工作效率。

以算例4为例获得岸桥调度顺序：岸桥1的集装箱处理顺序为2-10-9-4-3；岸桥2的集装箱处理顺序为6-1-5-7-8；AGV1的集装箱处理顺序为9-8；AGV2的集装箱处理顺序为2-7；AGV3的集装箱处理顺序为6-5； AGV4的集装箱处理顺序为10-4；AGV5的集装箱处理顺序为1-3。

2）大规模实验结果

TSGA和GA 的Matlab 求解的结果如表4所示。从大规模算例实验结果来看，当集装箱数量超过30个，TSGA和GA的求解时间相对小规模实验都有显著的增加，不同于小规模实验中，TSGA算法求解时间几乎均大于GA算法。在大规模算例中，TSGA算法的求解时间和GA算法的求解时间差距不大，甚至部分算例中TSGA算法的求解时间要短于GA算法。同时，TSGA算法求解的OFV值显著小于GA算法，更接近最优解，这就证明TSGA算法在求解大规模算例中相较于GA算法的优越性。通过算例10和算例13的比较，在任务数量一定的情况下，岸桥和场区数量一定，通过增加AGV的数量可显著降低OFV值，即提高港口作业效率。由算例17和算例18可得，当任务数量一定时，增加AGV的数量并未降低OFV值，这表明AGV的数量并非越多越好。AGV过多可能会产生拥堵等情况，造成效率的降低。当任务数逐渐增加时，相应的OFV值也显著增加。由于模型考虑了岸桥中转平台的容量限制，当集装箱数量过多时，也可能会造成AGV的等待导致时间延长、工作效率降低。综上所述，小规模和大规模实验中TSGA求解的OFV值均优于GA，同时TSGA的求解时间与GA相差不大，在大规模算例中的求解时间甚至少于GA求解时间。因此，证明了TSGA在求解此双层模型中的有效性。

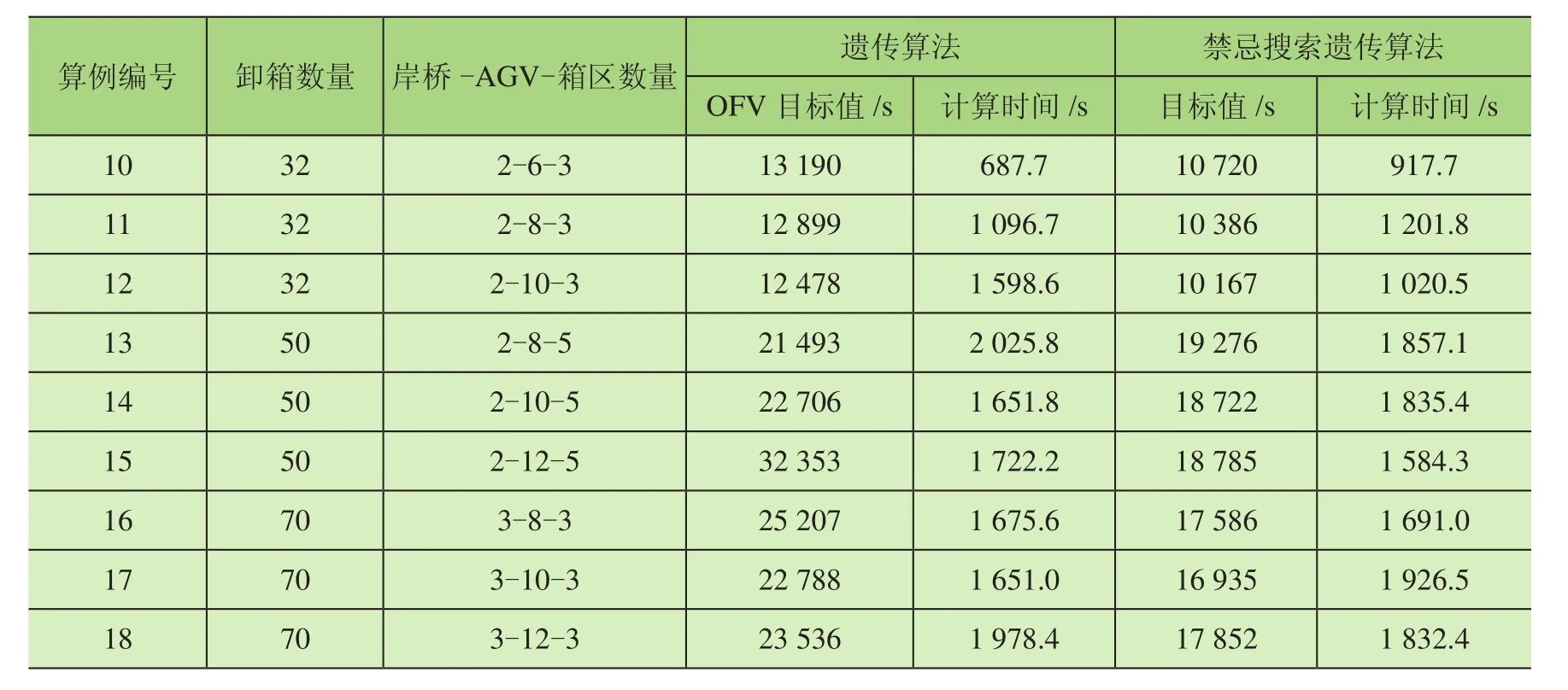
表4 禁忌搜索遗传算法和遗传算法对比(大规模)

图4显示了双层遗传算法的收敛性，以10个集装箱、5个AGV、2个岸桥为例，说明禁忌搜索遗传算法的收敛性的稳定性，充分说明了设计算法的稳定性。遗传算法的收敛速度越快，表明求解的工作时间越短，在实际自动化港口码头中，更高的工作效率极为重要。图5为AGV最短路径规划的调度图。

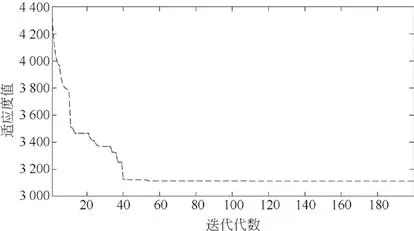
图4 典型遗传算法收敛图

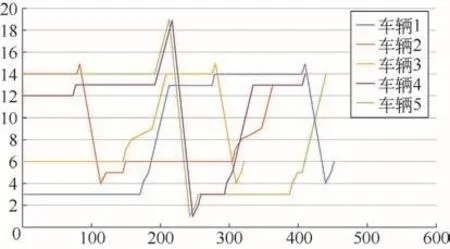
图5 典型AGV小车调度图

5 结论

本文研究了岸桥、AGV和ASC的综合调度问题，并进行装卸和卸载操作，建立了双层模型，模型中岸桥和AGV的调度被放在上层模型，其目标是尽可能减少集装箱的完工时间，以降低船舶停靠在岸的时间，同时结合实际约束了岸桥中转平台的容量为2个集装箱。模型的下层为AGV的路径规划，目标为AGV行驶的路径最短。此类问题通常可通过遗传算法进行求解，但随着任务数量的增加和岸桥AGV数量的变化，遗传算法可能会出现早熟情况，导致最优解的求解不准确。因此，对遗传算法加以改进，设计了禁忌搜索遗传算法对该问题进行求解。结果表明，在小规模的实验中证明了TSGA所求得的最优解要好于GA，同时TSGA的计算时间也与GA类似。证明了所提模型和算法的有效性，并能减少装卸时间，提高码头工作效率。