UHTC 功能梯度湿接缝的抗冲击性能

梅若诗，王 凯，余国庆，郭柳君

（华东交通大学土木建筑学院，江西 南昌 330013）

预制桥面板湿接缝因其便于工人施工并能显著缩短工期的特点而被广泛应用于桥梁工程中[1]，作为桥梁上的关键受力构件[2]，在其服役过程中，不可避免地会承受落石、 跳车现象等冲击荷载作用，从而导致湿接缝尤其是纵向湿接缝部位发生开裂、塌陷等病害现象， 进而将严重影响桥梁的使用寿命。 对预制桥面板湿接缝进行抗冲击性能的研究并预测其破坏寿命，改进湿接缝设计方案以延长破坏寿命，减少维修费用，具有十分重要的实用意义和科学研究价值。

超高韧性混凝土（ultra-high toughness concrete，UHTC，也称超高性能混凝土）是一种新型的混凝土结构建筑材料，因其优越的机械性能和材料性能被逐渐应用于桥梁工程中。 针对UHTC 的力学性能及其配比设计已有诸多研究报道[3-15]，并取得了许多积极的成果。 然而，这类研究都忽略了制作UHTC 的材料需要较高的成本，这大大限制了UHTC 在桥梁工程中的广泛应用。

已有研究表明，UHTC 对混凝土结构整体抗拉强度的提高效果明显优于抗压强度的提高效果[16]，整个混凝土结构均为成本较高的UHTC 显然是不经济合理的。 由此提出了UHTC 功能梯度混凝土这种多层混凝土结构的概念[17]。 目前对功能梯度混凝土的研究主要集中在对其抗弯性能、抗剪性能以及断裂性能等[16，18-21]，而对UHTC 功能梯度湿接缝这种UHTC 与素混凝土（normal concrete，NC）协同受力的组合结构的抗冲击性能及其冲击寿命的相关预测还不够。 同时存在大量研究表明[22-24]，湿接缝的破坏主要发生湿接缝受拉侧。 结合技术经济性考虑，本文引入功能梯度组合结构设计理念将预制桥面板湿接缝纵向受拉部分NC 替换成UHTC， 形成一种预制桥面板UHTC 功能梯度湿接缝，图1 为预制桥面板UHTC 功能梯度湿接缝设计示意图。 本文通过落锤冲击法研究了UHTC 功能层相对厚度以及UHTC 层抗压强度的大小对湿接缝模型试件的抗冲击性能的影响，同时结合试验数据建立终裂冲击寿命预测数学模型。

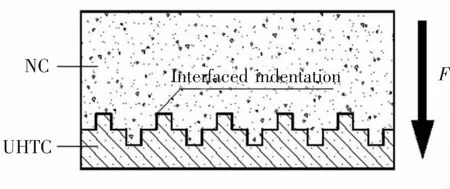
图1 预制桥面板UHTC 功能梯度湿接缝设计示意图Fig.1 Schematic diagram for designing wet joint of functional gradient of prefabricated bridge deck UHTC

1 试验概况

1.1 原材料

本试验所用原材料： 江西海螺水泥有限公司生产的42.5 级普通硅酸盐水泥（C）；南昌产石灰岩质碎石（G），粒径5～10 mm 连续级配；赣江江砂（S），细度模数为2.8，属于Ⅱ区中砂；南昌市火电厂生产的Ⅰ级粉煤灰（FA），平均粒径65.71 μm；江西钢厂产的S95 级矿粉（SL），平均粒径49.52 μm；挪威埃肯公司生产的中密质硅灰（SF），平均粒径0.1 μm；精细石英砂（QS），SiO2含量大于97%，粒径0.3～0.6 mm；江苏博特新材料有限责任公司产的JM-PCA（Ⅰ）型高效聚羧酸减水剂（PC）；江苏博特新材料有限公司生产的SBT-SRAⅠ系列混凝土减缩剂（SRA）；纤维是由钢纤维（STF）和聚丙烯纤维（PP）按比例混杂而成，两种纤维形态如图2。 纤维特征参数见表1，其中：fy为抗拉强度；Eu为弹性模量；D 为纤维直径；L为纤维长度；δ 为纤维吸水率。

表1 纤维性能指标Tab.1 Fiber performance index

图2 纤维种类Fig.2 Fiber type

素混凝土按强度等级C40 进行配制，其质量配合比水泥∶粉煤灰∶砂∶粗骨料∶减水剂∶水为1∶0.112∶1.739∶2.720∶0.003∶0.371。 为研究抗压强度对UHTC湿接缝抗冲击性能的影响，设计出4 种不同抗压强度的UHTC，配比见表2。

表2 超高韧性混凝土配合比Tab.2 Proportion of UHTC kg/m3

1.2 试件制作

立方体抗压试验采用150 mm×150 mm×150 mm标准。 抗冲击性能试验采用落锤法进行评价。 落锤法模型试件尺寸为150 mm×150 mm×40 mm。 为研究不同UHTC 功能层相对厚度对超高韧性湿接缝抗冲击性能的影响，共制备了5 种不同UHTC 功能层相对厚度的预制桥面板UHTC 功能梯度湿接缝模型试件。 抗冲击性能试验方案见表3，其中Hr为相对功能梯度厚度， 即UHTC 层相对总厚度的比值；fcu为UHTC 的抗压强度。

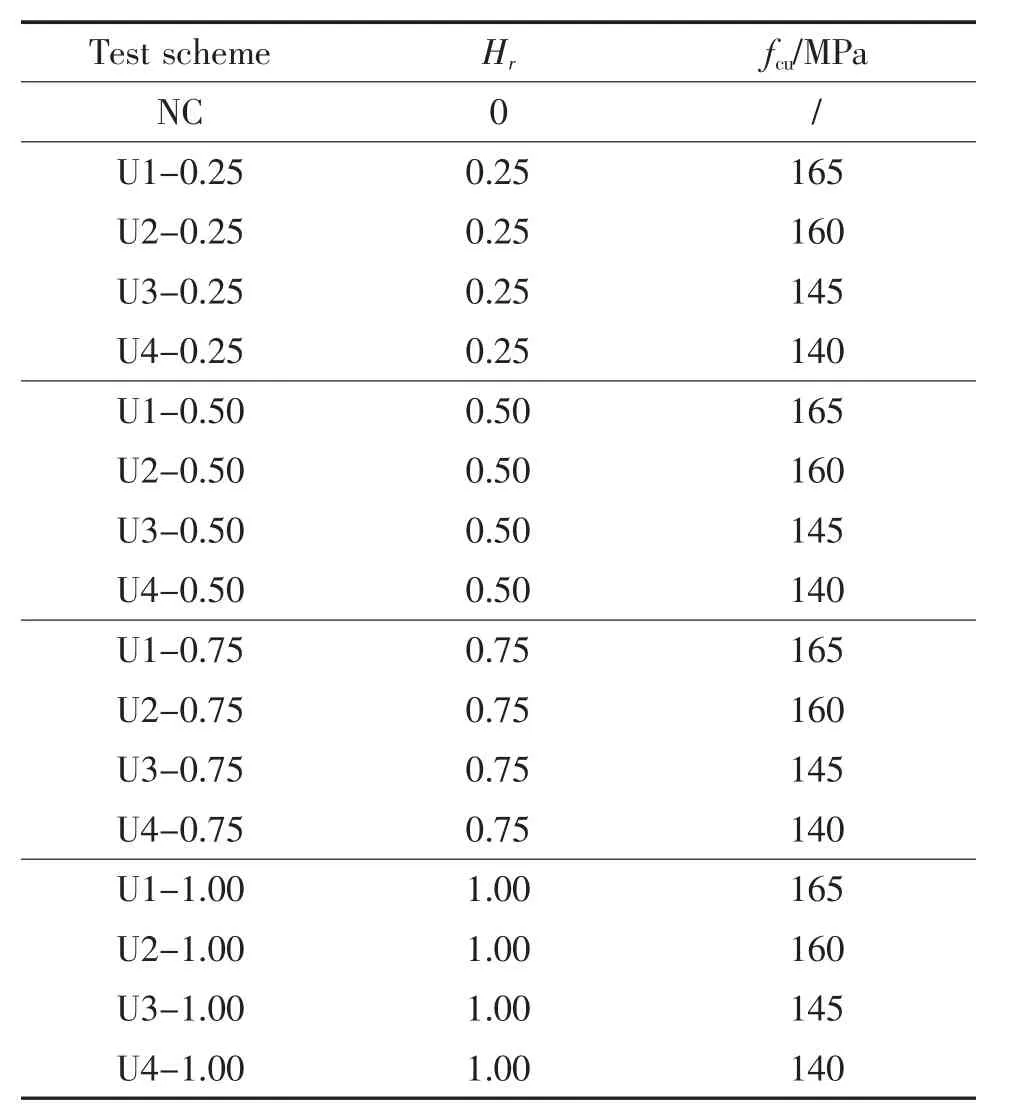
表3 抗冲击性能试验方案Tab.3 Impact resistance test scheme

本试验素混凝土与超高韧性混凝土均采用强制式搅拌机搅拌，其中对于超高韧性混凝土为防止纤维成团并保证其均匀分散至基体中，先将除纤维以外的混合料加入搅拌机干拌2 min， 然后加入50%的水以及全部减水剂和减缩剂的混合液搅拌1 min，再依次加入钢纤维和聚丙烯纤维湿拌2 min，最后加入剩余的50%的水搅拌6～7 min， 直至纤维分散均匀。 NC 单层体系模型试件和UHTC 单层体系模型试件一次浇注成型并充分振捣密实，而UHTC 功能梯度模型试件采用分层浇注法进行浇注。 在试模内先浇注普通混凝土层，当素混凝土充分振捣并达到预设层厚时，在其表面进行界面增强处理，随后浇注超高韧性混凝土并适当插捣。

1.3 试验方法

立方体抗压强度按CECS 13：2009 《纤维混凝土试验方法标准》[25]进行测试，测得其28 d 抗压强度。 落锤法冲击试验参照美国混凝土协会544（ACI544）提出的落锤法[9]，图3 为落锤法冲击试验示意图。 冲击过程中仔细观察试件表面，当试件表面出现第一条肉眼可见微裂缝时视为初裂，记此时的冲击次数为初裂寿命N1；继续冲击循环，当试件破坏至与4 块挡板中的任意3 块相接触时，视为试件破坏，记此时的冲击次数为终裂寿命N2；定义U 为冲击延性指数，表征混凝土初裂后的剩余抗冲击性能[26]；冲击耗能Ak也是描述构件抗冲击性能的重要指标之一，其定义式如下所示

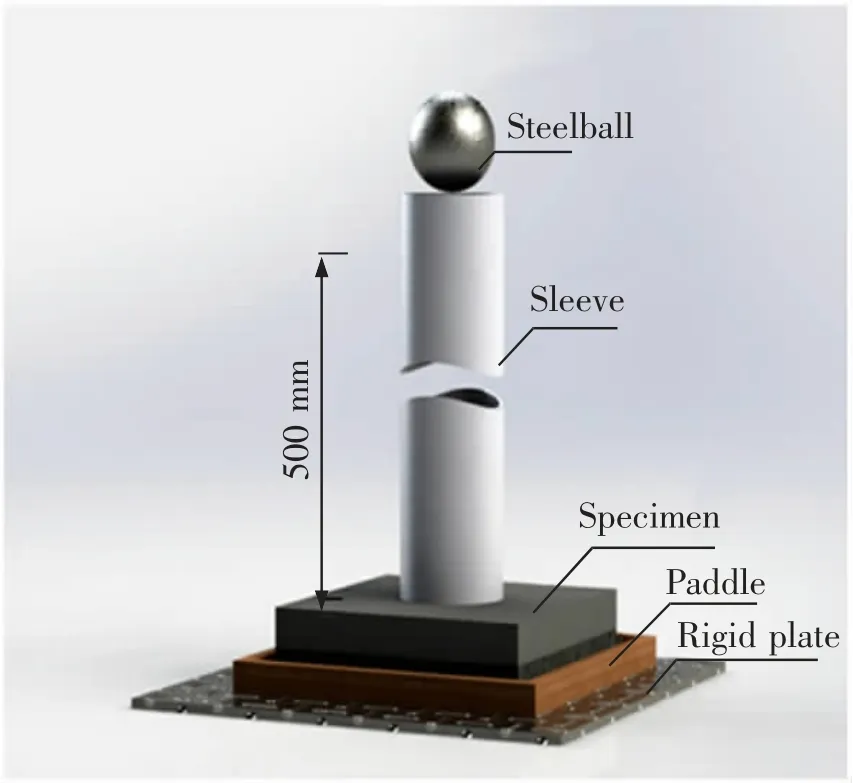
图3 落锤法冲击试验示意图Fig.3 Schematic diagram of impact test with drop-weight method

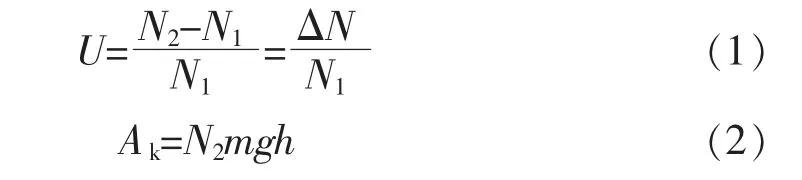
式中：m 为钢球的质量，本研究中取4.5 kg；g 为重力加速度，取9.81 N/kg；h 为钢球落距，本研究中取500 mm。

2 结果与讨论

2.1 破坏形态

对于冲击试验模型试件， 在冲击荷载的作用下，各试件组呈现出不同的冲击破坏形态。 图4 为冲击试验的破坏形态。 素混凝土试件NC 在表面出现1～2 条贯穿裂缝后完全断裂为2～3 块，均表现出明显的混凝土脆性破坏特征，这说明在冲击作用时素混凝土内部应力分布状态是不均匀的，导致局部应力过大而断裂； 对功能梯度混凝土试件和单层UHTC 试件，在表面出现第1 条裂缝后，未发生脆性破坏，仍然能继续承受冲击荷载作用，随着冲击次数的不断增加，产生新裂缝，而且随着原有裂缝继续扩展，直至试件破坏，出现3～4 条裂缝，将试件分成3～4 块，裂缝呈X 形分布，表现出明显的韧性破坏特征，在相同抗压强度条件下，随着UHTC 功能层相对厚度的增加，冲击荷载作用点附近的细小裂缝会更多， 而在UHTC 功能层相对厚度一定时，抗压强度越大， 冲击荷载作用点附近的细小裂缝越多。 以上表明，由于纤维的加入，混凝土基体由脆性破坏变为韧性破坏，试件发生开裂后，钢纤维和聚丙烯纤维对裂缝具有桥接的作用，纤维的拉断和拔出对冲击荷载产生的能量有一定的消耗作用，阻止裂缝的扩展， 提高了整个试件的延性与冲击韧性。综上，UHTC 功能层能有效改善结构的阻裂能力和抗冲击性能。

图4 模型试件冲击破坏形态Fig.4 Impact failure form of model specimen

2.2 冲击寿命

如图5 为fcu=165 MPa 时的初裂寿命N1以及初裂终裂寿命差ΔN 随UHTC 功能层相对厚度Hr变化的变化趋势。 由图5 可知，随着UHTC 功能层相对厚度的增加，初裂寿命N1与初裂终裂寿命差ΔN都有不同程度的增长，并且随着UHTC 功能层相对厚度的增加，2 种冲击寿命的增长速率也逐渐变大。

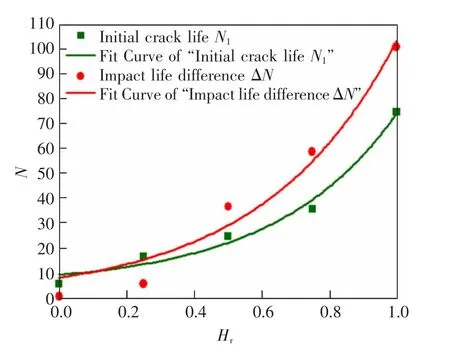
图5 冲击寿命与UHTC 功能层相对厚度的关系Fig.5 The relationship between impact life and relative thickness of UHTC function layer

预制桥面板UHTC 功能梯度湿接缝模型试件冲击寿命的增加表明其抗冲击性能增强。 试验结果表明冲击寿命N 可以表示为关于UHTC 功能层相对厚度的指数函数（图5），其函数表达式为

式中：a，b 和c 为与浇筑方式、养护条件以及素混凝土性能等试验初始条件有关的参数， 一般而言，当除UHTC 功能层相对厚度的试验条件确定时，a+b+c=const，而且这个常数等于素混凝土的理论终裂寿命；α 为与初裂前与混凝土的阻裂性能和抗冲击性能相关的参数， 定义为初裂前功能层厚度增效指数，用于表征UHTC 功能层相对厚度对混凝土的初裂前抗冲击性能的增效作用；β 为与初裂后与混凝土的阻裂性能和抗冲击性能相关的参数，定义为初裂后功能层厚度增效指数，用于表征UHTC 功能层相对厚度对混凝土的初裂后抗冲击性能的增效作用。 结合式（1）和式（3），可得终裂寿命N2计算公式

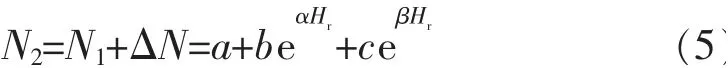
式中：β=α（1－Dimpact）。 定义Dimpact为冲击劣化因子，表示冲击荷载下，混凝土初裂后，功能层厚度增效指数的劣化作用。

将式（3）、式（5）代入式（2），得到超高性能功能梯度混凝土冲击延性关于UHTC 功能层相对厚度的函数为

已知U 的表达公式，将该公式作为拟合公式结合原始数据进行数据拟合得到相应的参数见表4。随着抗压强度的增大，Dimpact逐渐减小直至为负值。已知高性能混凝土中的纤维能降低混凝土表面水分蒸发速率， 并减小混凝土内外湿度差和温度差，从而减少混凝土因水分蒸发， 收缩作用引起的孔洞，进而提高混凝土的抗冲击性能。 这里在抗压强度为140 MPa 时Dimpact为负值，很大程度上可能是因为水胶比较大，UHTC 的强度不足，UHTC 中的纤维已经不能明显减少混凝土因水分蒸发、收缩作用引起的孔洞以抵抗混凝土初裂后的裂纹扩展。

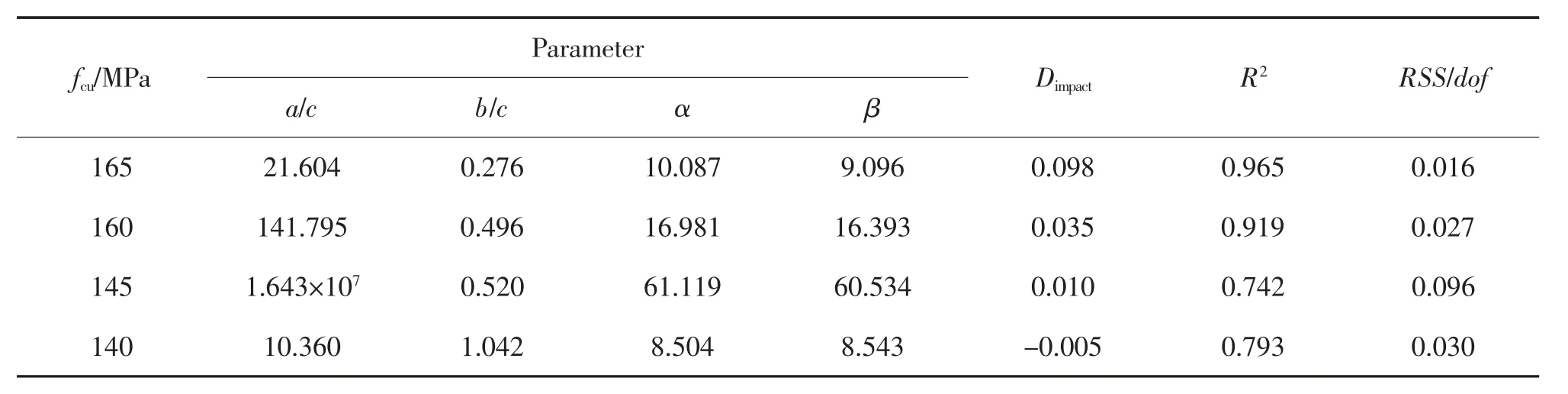
表4 湿接缝模型试件冲击延性拟合系数Tab.4 Fitting coefficient of impact ductility of wetjoints model specimens

2.3 冲击耗能

根据图6， 对各组湿接缝模型试件的冲击耗能Ak进行对比分析。 由图6 可以看出：对于UHTC 功能层厚度相同的模型试件， 其Ak随着UHTC 抗压强度的增大而增大，且增大幅度随着UHTC 抗压强度的增大而增大。 当UHTC 功能层相对厚度Hr为0.50，抗压强度从165 MPa 减少到140 MPa 时，湿接缝模型试件Ak分别降低了10.2%，22.0%和43.5%。此外， 随着UHTC 功能层相对厚度的增加Ak的降低率增大。 这表明其UHTC 功能层对湿接缝抗冲击性能具有较好的增强效应。

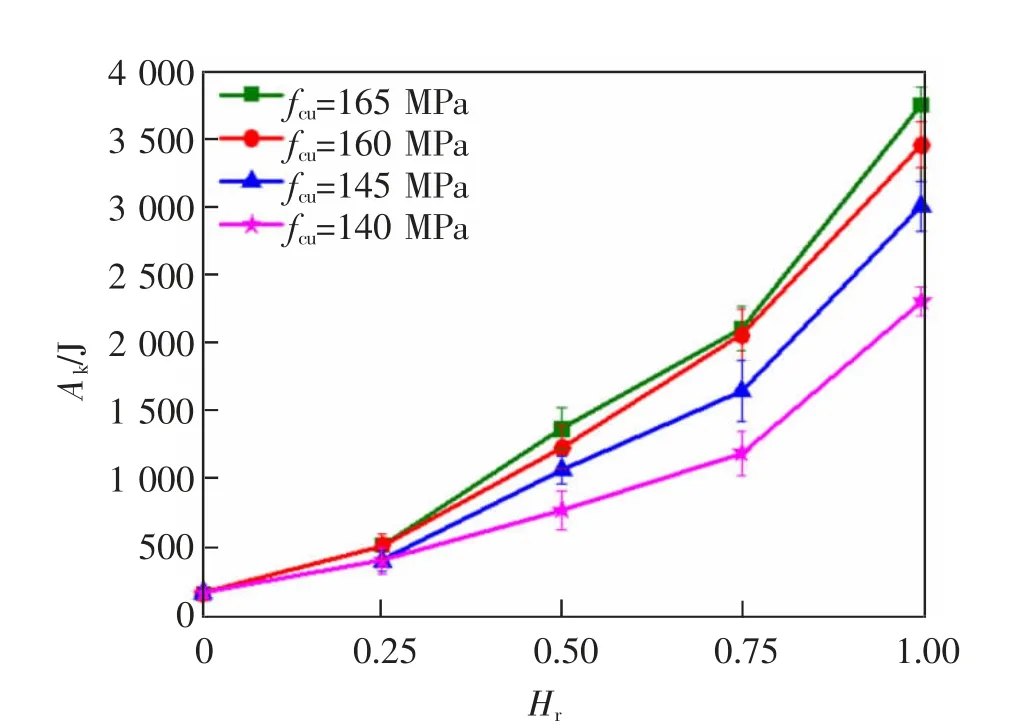
图6 冲击耗能Fig.6 Impact energy

2.4 初裂与终裂冲击寿命间的关系

如图7 为不同抗压强度下初裂寿命N1与终裂寿命N2的关系。 由图7 可知，初裂寿命和终裂寿命存在某种线性相关性， 并且随着抗压强度的增加，这种线性关系的斜率也在减小。

试验结果表明终裂寿命可以表示为关于初裂寿命的线性函数（图7），其函数表达式为

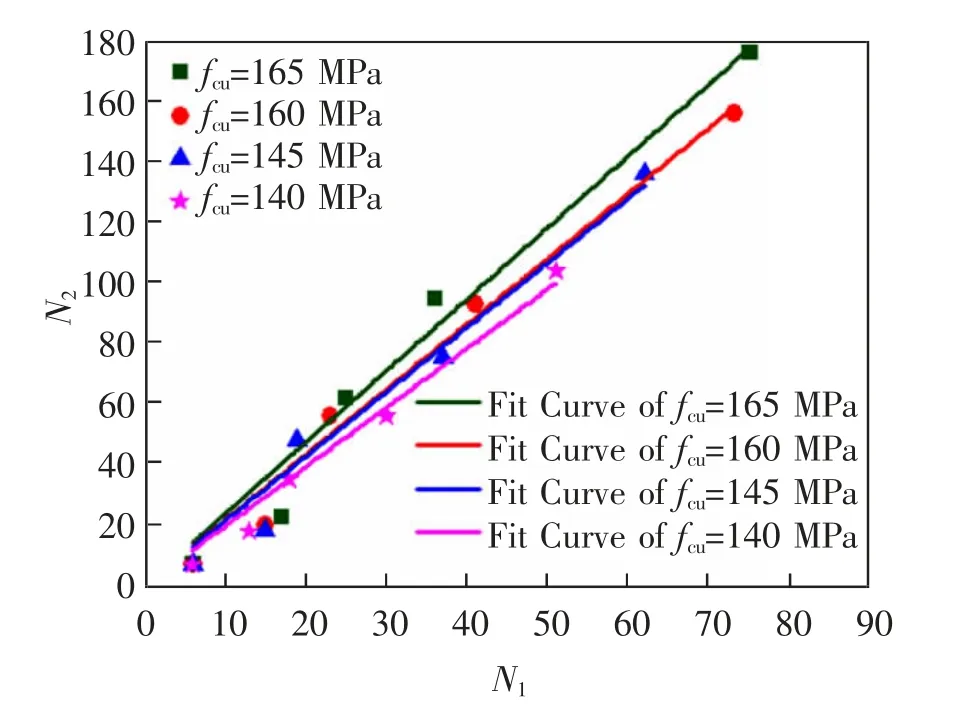
图7 湿接缝冲击寿命间的曲线拟合Fig.7 Curve fitting between the impact life of wet joints

式中：B 为与抗压强度相关的参数。

如表5 为不同抗压强度下的参数B。随着抗压强度的增大，B 逐渐减小， 在抗压强度为145～160 MPa时参数B 变化不大， 这表明在该抗压强度范围下，终裂寿命受初裂寿命的影响反应并非十分强烈。

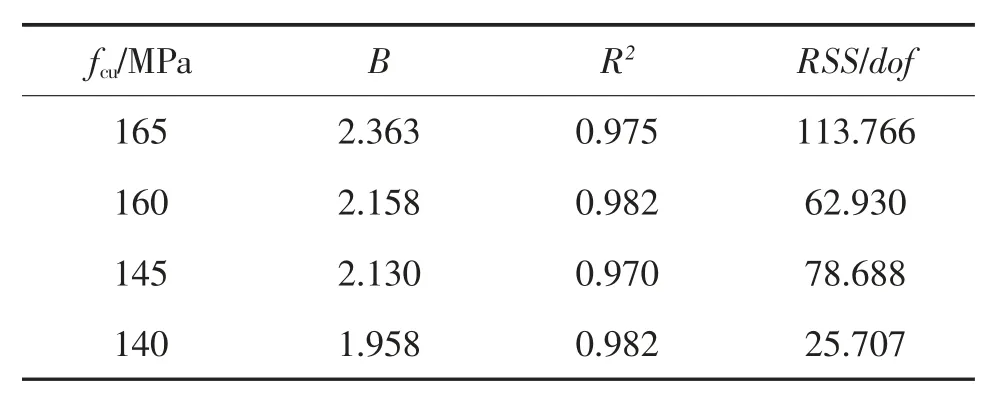
表5 湿接缝模型试件冲击寿命线性拟合系数Tab.5 Fitting coefficient of impact life of wetjoints model specimens

2.5 灰色关联分析

2.5.1 灰色关联分析方法

为了进一步研究相对功能厚度、抗压强度以及初裂寿命对预制桥面板UHTC 功能梯度湿接缝抗冲击性能的影响程度，衡量各因素影响程度的相对主次顺序，本文选择邓聚龙教授[27]提出的灰色关联分析模型进行分析。 关联分析作为灰色系统理论中应用广泛的分支，其基本思想是根据序列曲线几何形状的相似程度来判断其联系的紧密程度。 该方法能够在信息受限、关系模糊的情况下，通过无量纲化处理使无序的数据转变为有规律的数据，分析并确定多个自变量与多个因变量的关联程度[27-28]。

设参考数列X_0={X_0 （1），X_0 （2），X_0（3），…，X_0（n）}（在本文中即是终裂寿命数据列）；设比较数列X_i={X_i（1），X_i（2），X_i（3），…，X_i（n）}(i=1，2，3)（在本文中指的是UHTC 功能层相对厚度数据列、抗压强度数据列以及初裂寿命数据列）。

因为每组数列代表的不同的物理意义，量纲以及数量级会有很大的差异，若强行直接进行计算分析，得到的关联度系数之间没办法比较，对各数据列进行无量纲处理。 本文采用初值化的无量纲化处理方式得到新一组的参考数列和比较数列，计算过程如下

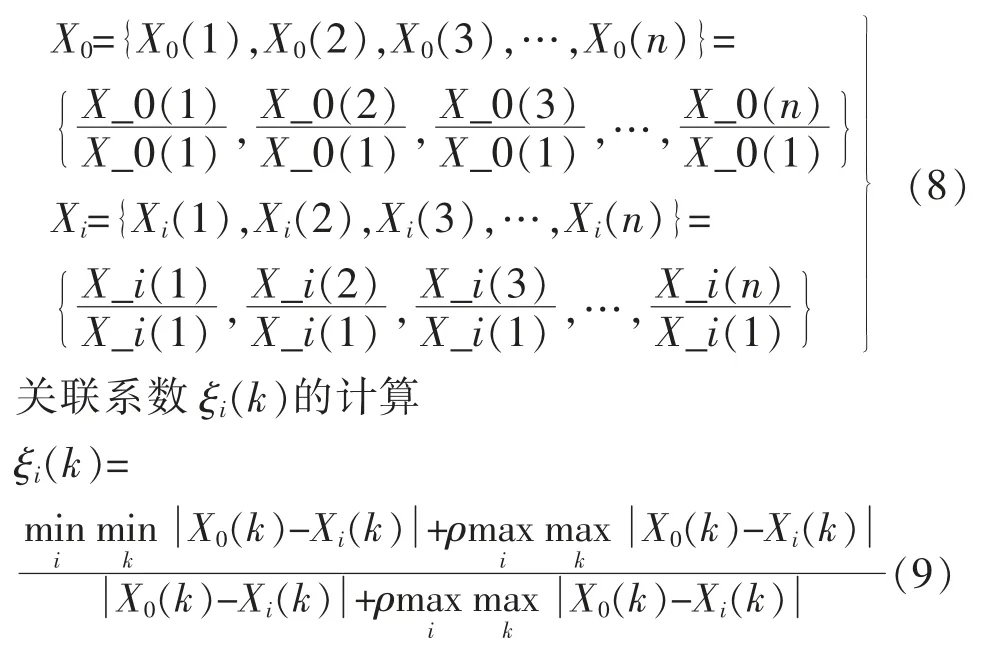
式中： 本文中i=1，2，3；k=1，2，3， …，n；ρ 为分辨系数，用来提高关联系数之间的差异性显著性，这里取ρ=0.5。

2.5.2 灰色关联分析结果

根据灰色关联分析步骤和落锤法冲击试验结果，确定灰色关联分析原始数据列，见表6。 原始数据列进行无量纲化处理后，结果如表7 所示。

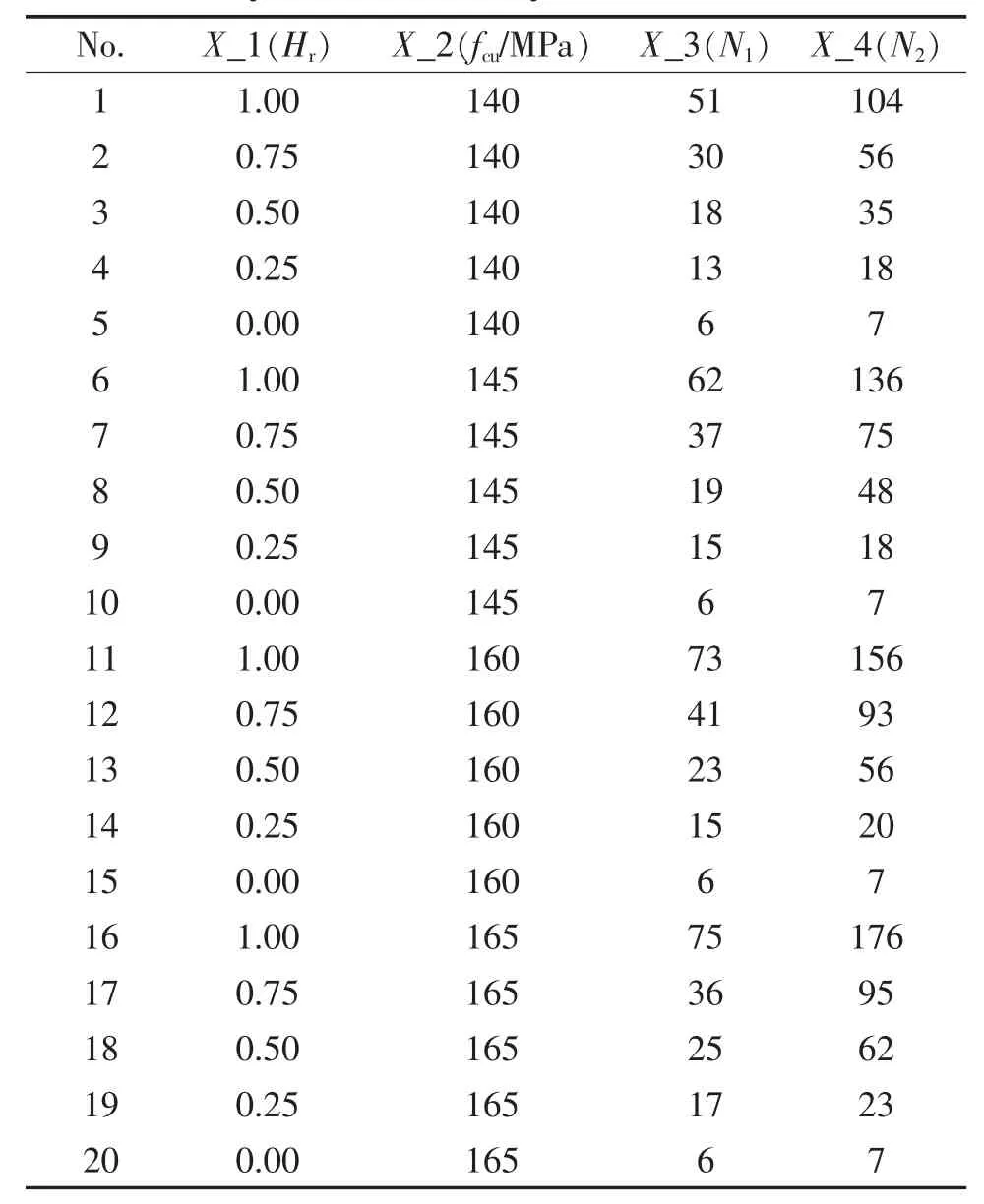
表6 灰色关联分析原始数据列Tab. 6 Gray correlation analysis on raw data columns

表7 原始数据列初值化Tab.7 Initialization of raw data columns

利用软件Matlab 计算UHTC 功能层相对厚度、抗压强度、初裂寿命与终裂寿命的灰色关联系数ξ 和关联度R，结果如图8 和表8 所示。 由表8可知，3 种影响因素对终裂寿命的影响程度由强到弱排列为：N1>Hr>fcu>0.5，前两个关联度均大于0.8。说明初裂寿命以及UHTC 功能层相对厚度对终裂寿命的影响十分显著， 其中初裂寿命的影响最大。 抗压强度的关联度为0.510，其对终裂寿命影响较显著。

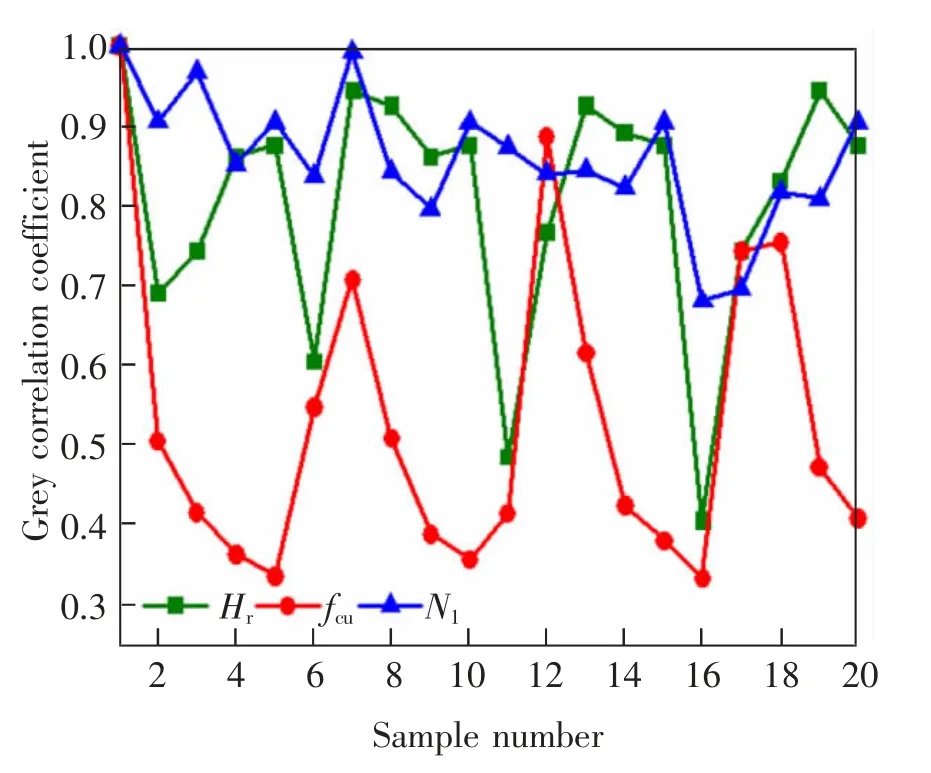
图8 灰色关联系数Fig.8 Gray correlation coefficient

表8 各因素与破坏冲击寿命的关联系数及关联度Tab.8 Correlation coefficient and degree between abrasion loss and various factors

3 UHTC 终裂冲击寿命多因素预测模型

灰色关联分析表明，各因素对终裂寿命的影响都较为显著；因此在建立终裂寿命多因素模型时需要综合考虑各个因素的影响。

3.1 预测模型建立

根据冲击寿命与功能层厚度典型关系推导出的冲击延性关于UHTC 功能层相对厚度的关系式（5）， 转化为终裂寿命关于UHTC 功能层相对厚度的关系式

图9 Dimpact 回归曲线Fig.9 The regression curve of Dimpact

将式（11）代入式（10）得到第一种终裂寿命预测数学模型（Model_Ⅰ）

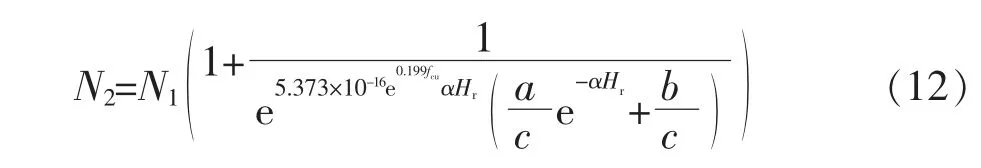
在2.4 节中， 求得终裂寿命与初裂寿命的关系表达式（7），关系式（7）在形式上比关系式（10）要更加简单， 但其未考虑UHTC 功能层相对厚度的影响，而初裂寿命在一定程度上也受到功能层厚度的影响， 可由初裂寿命和抗压强度作为影响因素预测预制桥面板UHTC 功能梯度湿接缝的终裂寿命。其中，与抗压强度fcu有关的参数B 的回归曲线如图10，由图可得到参数B 的回归表达式为

图10 参数B 回归曲线Fig.10 The regression curve of parameter B

将式（13）代入式（7）得到第2 种终裂寿命预测数学模型，命名为Model_Ⅱ

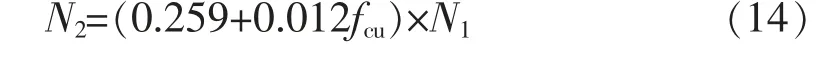
3.2 预测模型的检验与分析

将本文中预制桥面板UHTC 功能梯度湿接缝的终裂寿命预测模型Model_Ⅰ和Model_Ⅱ计算得到的预测值与湿接缝模型试件终裂寿命的试验值分别进行对比分析，结果如图11 所示。 图中的横坐标为模型试件终裂寿命的试验值，纵坐标分别为预测模型Model_Ⅰ和Model_Ⅱ计算得到的模型值，实线为试验值和模型值等值的参考线，另两条虚线表示变异系数为0.3 并且置信度为90%时磨损量模型值的上限与下限。由图11（a）得知，对于预测模型Model_Ⅰ，试验数据点分布在上下限以内且十分接近等值参考线，说明该预制桥面板UHTC 功能梯度湿接缝多因素计算模型能够较好地反映UHTC 功能层相对厚度、 抗压强度以及初裂寿命的关系；而对于预测模型Model_Ⅱ（图11（b）），虽然在终裂寿命较大，即湿接缝抗冲击能力较大时能够较好预测终裂寿命的大小，但在终裂寿命比较小，即湿接缝强度较弱时，模型值与试验值偏差较大。 在实际桥梁工程中，若已知UHTC 功能梯度湿接缝强度较大时，可用使用形式更加简单的预测模型Model_Ⅱ对终裂寿命进行粗略的预测，但若要对UHTC 功能梯度湿接缝的终裂寿命较为精细一些的预测，可采用吻合情况更加良好预测模型Model_Ⅰ。

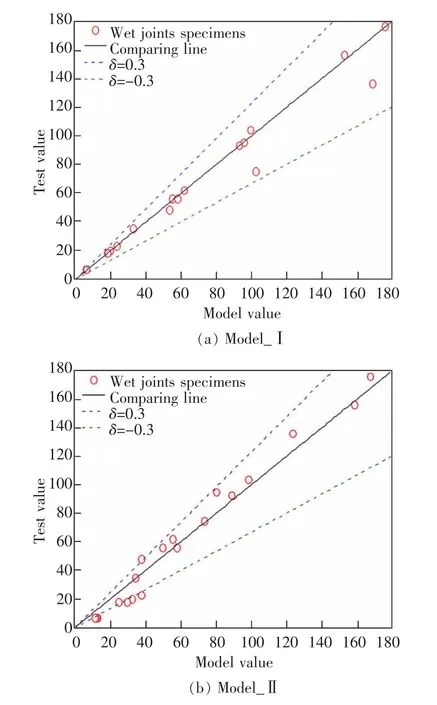
图11 湿接缝终裂冲击寿命的试验值与模型值Fig.11 Test value and model value of failure impact life of concrete

此外经计算得知，终裂寿命预测模型Model_Ⅰ和Model_Ⅱ模型值与试验值的比值的均值分别为μI=1.01，μⅡ=1.24，标准差σI=0.115 2，σⅡ=0.383 6，变异系数δI=0.113 6，δⅡ=0.309 7， 这表明上述预制桥面UHTC 功能梯度湿接缝终裂寿命多因素计算模型Model_Ⅰ的预测精度较高，适用性良好，而Model_Ⅱ的精度较差，适用性也相对较差。

4 结论

采用落锤法研究了UHTC 功能层厚度和UHTC抗压强度对预制桥面板UHTC 功能梯度湿接缝的抗冲击性能的影响规律，并结合试验数据建立破坏寿命预测数学模型，得出如下结论。

1） UHTC 功能层的设置可明显改善素混凝土湿接缝的抗冲击性能，使其由脆性破坏变为韧性破坏。 冲击寿命可以表示为关于UHTC 功能层相对厚度的指数函数，并在此基础上提出了关于UHTC功能层相对厚度的湿接缝模型试件冲击延性预测模型。

2） 对于UHTC 功能层厚度相同的模型试件，其Ak随着UHTC 抗压强度的增大而增长，且增长幅度随着UHTC 抗压强度的增大而增大。 此外， 随着UHTC 功能层相对厚度的增加Ak的增长率越大。这表明其UHTC 功能层对湿接缝模型试件整体抗冲击性能具有较好的增强效应。

3） 在抗压强度一定时，落锤法冲击试验得到的终裂寿命可以表示为关于初裂寿命的线性函数。

4） 根据灰色关联分析，得到3 种影响因素对终裂寿命的影响程度由强到弱排列为：N1>Hr>fcu>0.5，前两个关联度均大于0.8，说明初裂寿命以及UHTC功能层相对厚度对终裂寿命的影响十分显著，其中初裂寿命的影响最大。 抗压强度的关联度为0.510，其对终裂寿命影响较为显著。

5） 基于冲击延性预测模型， 推导出了UHTC功能层相对厚度， 抗压强度以及初裂寿命共同影响下湿接缝模型试件的终裂寿命预测数学模型Model_Ⅰ。 基于落锤法得到的初裂寿命与终裂寿命线性相关性，推导出了抗压强度以及初裂寿命为影响因素的湿接缝模型试件的终裂寿命预测数学模型Model_Ⅱ。 将试验值与模型值进行比较计算，得出预制桥面UHTC 功能梯度湿接缝终裂寿命多因素计算模型Model_Ⅰ的预测精度较高， 适用性良好，而Model_Ⅱ的精度较差，适用性也相对较差。但在实际桥梁工程中，若已知UHTC 功能梯度湿接缝强度较大时， 可用使用形式更加简单的预测模型Model_Ⅱ对终裂寿命进行粗略的预测， 但若要对UHTC 功能梯度湿接缝的终裂寿命较为精细一些的预测，可采用吻合情况更加良好预测模型Model_Ⅰ。