分数阶捕食者−食饵模型的变分迭代法
2022-04-06岑达康汪志波
岑达康,汪志波
(广东工业大学 数学与统计学院, 广东 广州 510520)
近年来分数阶微分方程(Fractional Differential Equation, FDEs)的应用越来越普遍,如模拟反常扩散过程、波传播、湍流、生物系统等[1-2]。目前除了少数简单的FDEs外,大部分FDEs还不能找到其解析解[3]。因此,针对FDEs提出简单高效的数值算法是十分必要的。
求解分数阶微分方程的数值算法主要包括有限差分法、有限元法、级数逼近法(变分迭代法、Adomian分解法、同伦摄动法等)、移动网格法、矩阵转化法等。有限差分法[4-5]、有限元法[6-7]将方程离散化,从而得到方程的近似数值解。与它们相比,变分迭代法(Variational Iteration Method, VIM)不需要进行变换和数值逼近,是一种重要的近似解析方法。1978年,Inokuti等 [8]提出广义拉格朗日乘子法(Lagrange Multiplier, LM)。基于LM方法,何吉欢[9]于1997年提出了VIM方法。目前,VIM方法已广泛应用于非线性微分方程的近似逼近问题。尹伟石等[10]应用VIM方法求解Riesz分数阶偏微分方程。基于VIM方法,高秀丽等[11]成功模拟了Whitham-Broer-Kaup方程和mKdV方程两类非线性数学物理方程的行波解。姜兆敏等[12]用VIM求解二阶常微分方程组边值问题,并给出2个具体应用实例。
许多数学家和生态学家对捕食者−食饵(Predator-Prey, P-P)系统进行了深入的研究,建立了一系列数学模型,如Volterra模型、带自身阻滞作用logistic项的改进Volterra模型、Lotlak-Volterra模型等。分数阶微积分的非局部性质使其在模拟遗传性和记忆性现象上更具优势。因此,分数阶P-P模型越来越受到研究者的关注。El-Shahed等[13]研究了一类分数阶广义P-P模型的正平衡点的存在性、稳定性和极限环。王虎等[14]讨论了具有阶段结构的时滞分数阶P-P模型的稳定性,得到了平衡点的渐进稳定性条件和参数稳定区间。关于P-P模型的VIM方法研究,汪维刚等[15]利用一组泛函,选取拉格朗日乘子,用修正的变分方法,得到了相应模型的近似解。但是其并未对VIM迭代格式进行收敛性分析。由于分数阶模型的VIM方法研究相对较少,本文研究式(1)~(2)的分数阶捕食者−食饵模型的VIM方法及其收敛性。
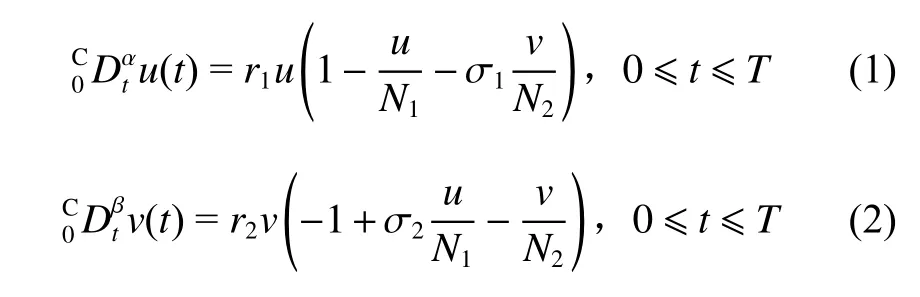
式(1)~(2)中:u和v分别为捕食者和食饵的种群密度,t为时间,T是t的最大时间。 α,β 分别为Caputo分数阶导数的阶数。r1为 食饵种群增长率,r2为捕食者种群死亡率,N1为 食饵种群环境容纳量,N2为捕食者种群环境容纳量, σ1为 供给比率, σ2为消耗比率。1 <α,β<2;u(0),v(0),u′(0),v′(0)已知。

式中:Γ是Gamma函数,τ为积分运算变量。

由式(3)可得式(1)~(2)的等价模型为

式中:

假设F,G满 足Lipschitz条件,存在常数C,使

1 变分迭代格式
对模型(4)~(5)构造式(6)~(7)的限制泛函。


2 收敛性分析
定 理1取u0(t)=ϕ(t),v0(t)=φ(t) ,其 中ϕ(0)=u(0) ,φ (0)=v(0)。由迭代格式(8)~(9)得到的近似解序列 {un(t)}和{vn(t)}收敛于模型(4)~(5)的精确解u(t)和v(t)。
证明易知u(t)、v(t)满足

记en(t)=un(t)−u(t) ,εn(t)=vn(t)−v(t)。由迭代格式(8)~(9),可得误差方程(10)~(11)。

显然有
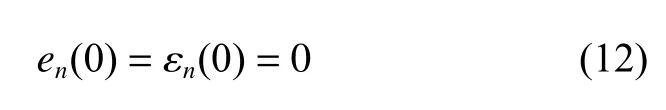
计算可得

代入式(12),有

由Lipschitz条件,有

3 数值模拟
例 1 考虑如下时间分数阶logistic模型
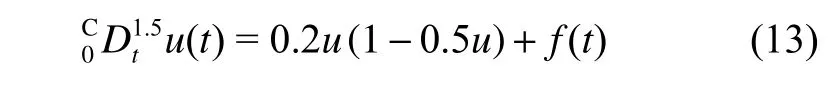
式中:f(t)=Γ(2.5)−0.2t1.5+0.1t3, 初值条件为u(0)=0,u′(0)=0; 精确解为u(t)=t1.5。
取u0(t)=0,得

表1列出了u0(t),u1(t)与精确解的绝对误差。
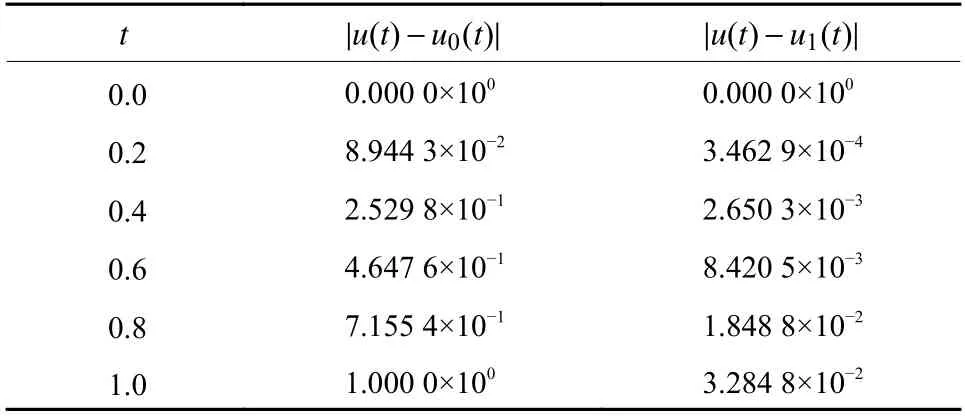
表1 例1的数值误差结果Table1 Numerical error results for Example 1
例 2 考虑如下时间分数阶捕食者−食饵模型

式(14)~(15)中:

初值条件为u(0)=v(0)=0,u′(0)=v′(0)=0,精确解为u(t)=t1.4。
v(t)=t1.6, 取u0(t)=0,v0(t)=0,算得

表2列出了u0(t),u1(t),v0(t),v1(t)与精确解的绝对误差。

表2 例2的数值误差结果Table2 Numerical error results for Example 2
4 结论
本文重点研究了一类分数阶捕食者−食饵模型。依据变分理论,对此类方程建立变分迭代格式,并严格地证明所建立格式的收敛性。最后,对2个模型进行数值模拟。模拟结果验证了该方法的可行性和有效性。
