直升机机身冲击损伤有限元分析

宋畅 岳巍

（中国直升机设计研究所，江西景德镇 333001）

0.引言

粘接的蜂窝夹层复合材料被广泛的用于直升机机身结构，如图1所示，蜂窝夹层结构具有比强度高、比刚度高、抗疲劳、可设计性强等优异特性，密度远小于金属，可为直升机减重25%-30%[1]。然而，蜂窝夹层结构对冲击损伤是极其敏感的，除了面临地面武器和空中武器的威胁，在执行日常任务时，机身常常受到沙石和冰雹等恶劣天气，从而造成冲击损伤[2]。冲击损伤破坏了复合材料夹层结构的完整性，造成大面积的脱粘和分层，进而降低其强度和刚度。因此，蜂窝夹层结构的冲击损伤阻抗及损伤容限已发展成为国内外的研究热点。

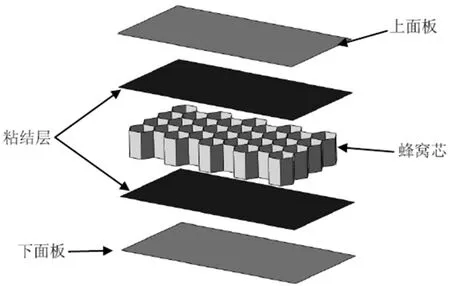
图1 蜂窝结构示意图

国内外学者开展了诸多复合材料抗弹性能的数值和试验研究。古兴谨[3]针对不同铺层角度的层合板的冲击损伤进行了分析，分别考虑纤维断裂、基体裂纹和分层等三种损伤形式。Raju等[4]采用不同尺寸的冲头对蜂窝夹层结构进行了冲击试验，探究其对冲击损伤的影响。Fatt和Park[5]对蜂窝夹层结构冲击的能量耗散机制进行了研究，发现下面板在冲击过程中所吸收的能量较多，损伤更为严重。国内外针对复合材料层合板冲击问题的研究较为广泛，但是对蜂窝夹层复合材料在较低能量下的冲击损伤研究较为缺乏，在冲击载荷下的损伤过程和机理的研究有待发展。

本文基于ABAQUS建立蜂窝夹层结构冲击的数值分析模型，通过编写VUMAT子程序实现了双向编织复合材料面板的渐进损伤分析，包括损伤起始、扩展以及刚度折减。将薄面板蜂窝夹层结构冲击损伤有限元仿真分析与试验结果进行对比，为直升机机身的抗冲击设计提供参考。

1.损伤模型和失效准则

自20世纪初60年代以来，科学家对复合材料进行了大量的研究，针对不同材料对象和应用对象提出多种强度准则，如早期的最大应力强度准则和最大应变强度准则、蔡-希尔强度准则、蔡-吴张量准则等。随着研究的进展，大量的试验结果表明，纤维增强复合材料的破坏模式分为纤维控制的失效模式和基体控制的失效模式，纤维控制的失效模式包括纤维方向的压缩屈曲破坏和拉伸破坏，基体控制的失效模式除了压缩和横向拉伸破坏之外，还有面内剪切破坏。根据上述特点，Hashin[6]分别考虑纤维以及基体的失效模式，基于应力提出了应用广泛的Hashin失效准则，当失效因子小于1时，材料并不是完全失去了承载能力，而是根据其损伤形式对刚度进行退化处理，当失效因子大于1时，材料发生破坏。由于Hashin准则针对单向纤维的复合材料，本文研究的蜂窝夹层上下面板为双向编织层合板，由于其结构完整型较好，强度及损伤容限较高，Hashin准则偏于保守，因此采用Yen[7]提出的编织结构复合材料损伤起始准则—Yen失效准则进行仿真，并与试验结果进行对比。

复合材料受冲击时受力以及失效类型较为复杂，典型受力形式包括界面拉伸脱粘、界面剪切脱粘、面内拉伸、面外压缩、面外剪切等。Yen失效准则是基于应变的失效准则，分别考虑双向编织纤维经向和纬向的压缩失效和拉剪耦合失效，基体主导的面外压缩失效、面内剪切失效以及分层失效，应用了双向编织复合材料损伤起始准则，公式如下：

（1） 经向纤维拉剪耦合失效

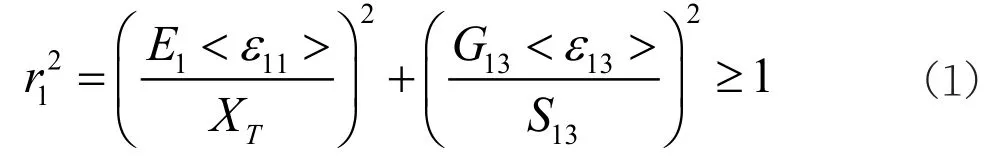
（2） 纬向纤维拉剪耦合失效

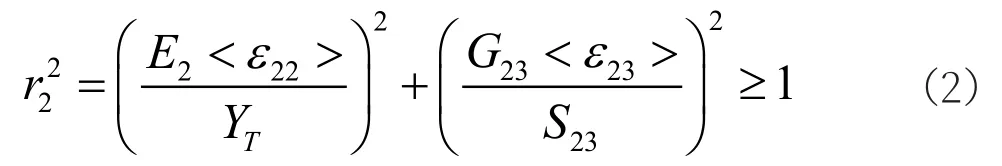
（3） 经向纤维压缩失效

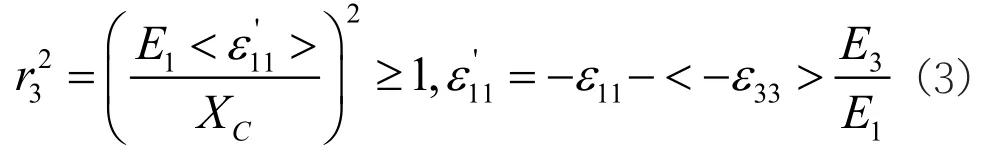
（4） 纬向纤维压缩失效

（5） 面外基体压缩失效

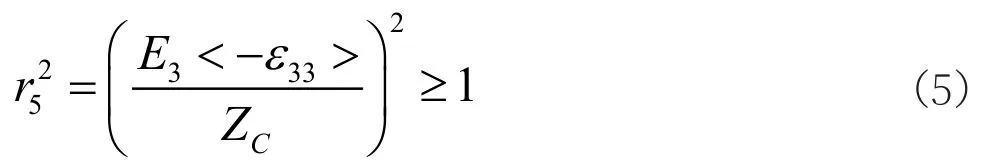
（6） 基体剪切破坏

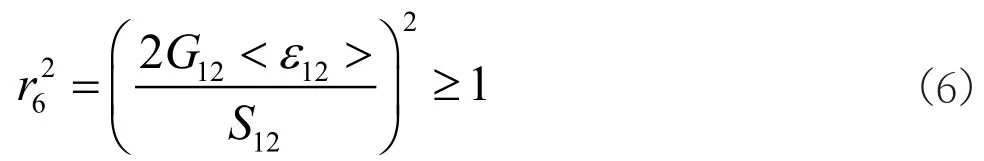
（7） 分层失效

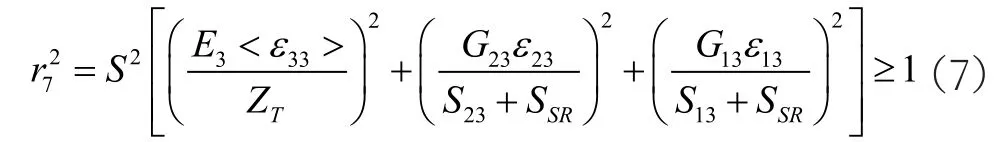
ri(i= 1,2,… …,7)是分别为上述7种失效模式的失效因子，E、G、ε分别代表了复合材料弹性模量、剪切模量以及应变，X、Y、Z、S分别代表双向编织复合材料三个方向的压缩强度、拉伸强度以及剪切强度。

当应变水平满足失效准则后，即Max[ri(i= 1,2,… …,7)] ≥1，材料损伤起始，结构承载能力下降。因此，对材料的进行刚度折减，常用的两种方法为常数折减和函数折减，常数折减即材料损伤起始后刚度立即折减至某一定值，函数折减则为材料损伤起始后，随着损伤不断累积，刚度持续减小。研究表明，在冲击载荷的作用下，采用刚度函数折减的方法进行渐进损伤累积计算的结果与试验情况更为相符。因此，本文采用函数折减的方法，Yen失效准则的损伤变量dI计算公式如下：

rI为损伤起始准则计算得到的失效因子，m为应变软化系数，根据经验m取值为4，用于反映材料的损伤扩展特性。

单元刚度折减与纤维和基体的损伤有关，因此将损伤变量分为3类，纤维拉剪损伤、纤维压缩损伤、基体损伤。其中d1=Min[r1，r2]，为纤维拉剪损伤变量；d2=Min[r3，r4]，为纤维压缩损伤变量 ；d3=Max[r5，r6，r7]，为面外基体损伤变量。采用式（9）的函数进行刚度折减，模拟复合材料层合板的渐进失效。

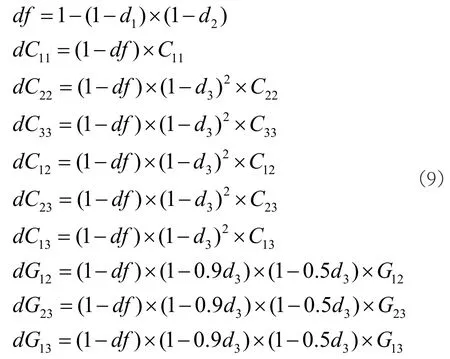
损伤变量随着失效因子的不断增大而增大，并逐渐趋近于极限值1，当纤维拉剪损伤变量d1或纤维压缩损伤变量d2为1时，材料完全失效并破坏，不再提供刚度。

2.蜂窝冲击有限元模型

本文使用ABAQUS的VUMAT用户子程序和显示动力学分析（Dynamic,Explicit）对复合材料薄面板蜂窝夹层结构进行冲击损伤分析，使用Yen失效准则对单元进行失效判定，在分析过程中删除失效单元。

有限元模型分别建立冲头、上下面板、蜂窝和胶层，如图2所示。半球形冲头直径为12.7mm，设置为刚体（Analytical rigid）并加入质量点；上下面板为双向纤维编织复合材料，定义用户材料，将弹性常数、泊松比、剪切模量、阻尼、拉伸强度、压缩强度、剪切强度等力学常数输入；蜂窝芯高度为20mm，采用等效建模方法，根据蜂窝结构等效理论，求得材料参数，采用工程常数定义为各向异性材料，同时基于蜂窝受压变形的四个阶段，即弹性阶段、软化阶段、压溃阶段和密实化阶段，将蜂窝定义为弹塑性模型，加载初始为弹性材料，达到屈服应力后，应力-应变关系为非线性，卸载后会产生永久的塑形变形，将试验测得的应力应变曲线输入模型，模拟蜂窝冲击的失效过程；在面板的层与层、面板与蜂窝间使用Cohesive单元模拟胶接，通过定义材料属性和截面，将Cohesive单元赋予Cohesive截面属性，设置损伤演化并输入失效应力，以此模拟胶层。不同材料层与层之间采用共节点的方法连接。上下面板和蜂窝使用三维应力线性减缩积分单元（C3D8R），胶层使用线性三维Cohesive单元（COH3D8）。

图2 蜂窝冲击有限元模型

动力学显式求解采用ABAQUS/EXPLICIT分析步，时间为10ms，并设置阻尼使计算更快的收敛。边界条件为上下面板边界完全固定，在冲击方向，利用预定义场（Predefined field）将冲头赋予初始速度，冲头的能量为0.9J。冲击过程中的接触问题是复杂的，采用Surfaceto-surface的方法建立接触，冲头的外表面为主面，蜂窝中心处直径稍大于冲头直径的圆柱区域节点集为从面，接触属性为硬接触，摩擦系数取0.1。采用运动接触法和有限滑移方式，在冲击过程中不断更新从面节点和主面的接触情况。

冲击后蜂窝的位移云图如图3所示，面板表面出现纤维损伤断裂，蜂窝芯体出现凹坑，表面基体存在压缩损伤，损伤区域直径为8mm，如图4所示。将仿真结果与试验结果进行对比，蜂窝受冲击过程中凹坑深度及半球形冲头速度随时间变化的曲线如图5、图6所示，有限元模拟的蜂窝冲击过程与试验结果吻合良好，试验的凹坑深度为1.24mm，仿真为1.35mm，试验的半球形冲头反弹速度为0.39m/s，仿真为0.50m/s，由于仿真环境较为理想，未考虑试验过程中摩擦等因素，导致试验与仿真存在一定误差。

图3 冲击后蜂窝的位移云图

图4 面外基体压缩损伤

图5 凹坑深度-时间曲线

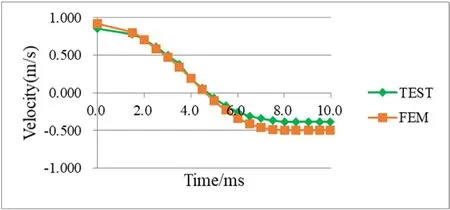
图6 半球形冲头速度-时间曲线

3.结论

本文建立了直升机机身蒙皮冲击损伤的有限元模型，并将试验结果与仿真结果进行对比，验证了有限元模型的有效性和准确性。使用ABAQUS建立薄面板蜂窝夹层结构的有限元模型，基于VUMAT用户子程序，采用Yen失效准则模拟面板的损伤起始和损伤扩展方式，将蜂窝芯体等效为弹塑性模型，并使用Cohesive单元模拟层间胶接。在低能量冲击下，冲击损伤表现为面板凹坑、少量纤维断裂、基体损伤并出现分层。对比分析薄面板蜂窝夹层结构冲击过程中凹坑深度及半球形冲头速度随时间变化的曲线，有限元结果与试验结果吻合良好。通过建立有限元模型模拟冲击的损伤过程和机理，预测损伤程度及范围，为直升机机身蒙皮的抗冲击设计提供依据。