基于供需双边模式的服务方案高效构建方法
2022-04-04徐汉川王忠杰涂志莹徐晓飞
王 笑,徐汉川,王忠杰,涂志莹,徐晓飞
(哈尔滨工业大学 计算学部,黑龙江 哈尔滨 150001)
0 引言
随着大数据、云计算、物联网等理论和技术的快速发展,Internet上可用的软件服务越来越多,现实中的各类物理资源及人工服务也通过虚拟化和物联网技术被接入Internet,并与线上的软件服务建立协同和集成,这两个趋势使互联网上的可用服务数量急剧增加。与此同时,客户需求也越来越倾向于大粒度和个性化,涉及到的应用业务与数据体现出很强的复杂性、关联性与跨界性,单一的服务往往难以满足此类需求,通常需要多项服务的集成。这种跨越大量领域、服务、业务流程和规则的服务生态系统构成了服务互联网或大服务[1-2],其中用户对服务的需求海量且个性化,服务资源数量众多且跨领域,需要在海量需求和服务间进行服务匹配,通过聚合不同领域的服务,产生复合服务解决方案,以满足用户需求。例如,养老服务中,某老人患有糖尿病,不愿接受到养老院养老,而子女白天上班,无法照顾老人。通过构建服务解决方案,可以将护工预约、护工日常护理、健康商城、老人健康档案、慢病管理、医院就医等跨领域和组织的服务整合在一起提供给老人,满足老人的居家养老需求。因此,如何高效构建用户满意的服务方案是服务互联网中服务设计和优化的核心问题。
服务方案构建的核心问题是在可用服务与用户需求间建立匹配关系,即服务供需双边匹配。研究人员已对服务供需匹配问题进行了大量研究,传统服务组合[3]和服务选择[4]技术将每个用户需求视为独立的个体,以某个或某些目标最优化为目标,在满足约束的前提下,根据现有可用服务构造出用户满意的优化服务解决方案。典型方法包括精确算法[5-6]、演化算法[7-11]、基于深度学习的算法[12-13]以及将服务组合问题转化为经典规划问题[14-15]与基于图的方法[16-17]。CHATTOPADHYAY[18]对服务组合问题提出一种近似机制来获得接近于最优解的时间。RODRIGUEZ-MIER等[6]提出一种使用精确算法的方法,该方法使用一种混合的局部—全局策略来优化QoS感知服务组合问题。HAYTAMY等[10]提出一个基于深度学习的服务组合框架,该框架融合了长短期记忆人工神经网络(Long Short-Term Memory, LSTM) 和粒子群优化算法。ZHOU等[8]在云制造领域中提出了解决多目标服务组合问题的自适应多种群差分人工蜂群算法。但是,在服务互联网场景下,用户需求和服务资源数量庞大,算法搜索空间巨大,现有的服务组合和服务选择技术难以高效快速地得到满足大规模个性化用户需求的服务方案。经过大量的实践观察和分析,发现服务与服务间、需求与需求间均存在相似性和关联性,某些领域服务也会频繁地在一起关联使用,如淘宝购物服务中,用户只能选择支付宝服务,而在京东购物服务中,只能选择微信或者京东钱包服务。这类相似性与关联性是领域服务先验知识的一种体现,如果能够挖掘出蕴含其中的关联关系,将历史上成功的可复用服务解决方案(服务模式)和用户经常提出的关联需求(需求模式)用于服务方案的构建和用户需求声明中,则可以将服务匹配的粒度从小粒度的原子服务和需求提升为大粒度的构建模块,有效缩减搜索空间,提升用户满意度。如果可刻画服务模式与需求模式间的关联关系,则可以进一步提高服务匹配的效率,实现服务方案的快速高效构建。
在现有研究中,通过数据挖掘技术从历史中挖掘模式已经成为服务组合中一种主导的方法[19-20]。PERRYEA等[21]在基于社区的服务组合方法中,利用历史上的复合解决方案尽可能地满足新的需求。LIU等[22]使用FP-growth算法从历史服务解决方案中挖掘服务模式。XU等[23]提出“需求—工程”(RE2SEP)两段式服务开发范型,对服务模式进行了定义,并提出了将需求模式与服务模式通过情境信息进行匹配。虽然当前已经有不少对服务模式的研究,但是对需求模式的研究还不足,只是根据用户提出的需求使用服务模式进行服务组合或者服务选择。同时,对于服务模式使用情境的研究较少,只是单纯使用历史出现的全部或部分服务流程进行复用。
另外,为了更好地理解用户需求,需要提供一种表达能力强且易于用户之间建模的需求模型。面向目标的建模技术常用于需求建模当中,ASADI等[24]提出一种基于描述逻辑的方法,在一个共同的知识库中表达模型之间的关系。ROLLAND等[25]和YU[26]将目标模型应用与需求工程的系统分析和设计以及信息和软件系统开发中。HORKOFF等[27]通过与功能和非功能目标的联系来分析和证明模型的正确性。但是,这些方法没有以服务开发为中心,而且必须对指定的目标模型进行人工分析,才能得到相应的候选服务[28]。同时,这些模型大多太过复杂,对于没有建模经验的终端用户,使用这些模型提出需求十分困难。
基于以上分析和思考,本文提出一种基于供需双边模式的服务方案高效匹配方法,其核心思想是挖掘领域先验知识中服务间、需求间以及服务与需求间的关联特征,利用模块化的思想提升服务匹配中供需双边构建单元的粒度,从而提高服务匹配效率和用户满意度。本文首先建立了基于双边模式的服务匹配问题模型;之后针对用户需求端,提出了基于意图树的需求和需求模式模型;针对服务提供端,提出了服务模式模型及挖掘策略;进而根据历史服务方案中的用户情境信息等内容构建了多维双边模式关联矩阵,并提出了关联矩阵的适应性更新策略;最后,针对3种典型的服务场景,设计了不同类型的算法,验证本文所提基于双边模式的匹配方法相较于传统方法的有效性。
1 基于供需双边模式的服务匹配问题模型与方法框架
1.1 基于供需双边模式的服务匹配问题模型
本文采用的优化策略是利用供需双边模式(服务模式与需求模式)及其关联矩阵来缩小搜索空间,提高匹配效率,实现服务方案的高效快速构建。由于最小化问题和最大化问题可以等价转化,服务互联网中基于供需双边模式的服务匹配问题模型可定义如下:
minF(x)=(Gu(x),Gs(x),Gp(x))T。
(1)
s.t.
hi(x)≤0,i=1,2,…,uh;
(2)
cpj(x)>0,j=1,2,…,|SSP|;
(3)
sspk≻sspl,k,l∈SSP。
(4)
其中决策变量x为服务方案,x=SSP,SEQ。其中:SSP为服务方案构造单元集合,由|SP|个服务模式sp和|S|个原子服务s构成,即ssp∈{sp1,sp2,…,sp|SP|,s1,s2…,s|s|},|SSP|=|SP|+|S|;SEQ为服务方案中构造单元间执行顺序集合,SEQ={seqij|sspi需要在sspj之前执行,sspi,sspj∈SSP}。式(1)为优化目标函数向量,根据目标诉求方可分为用户目标Gu(x),服务提供商目标Gs(x)以及第三方平台目标Gp(x),根据优化目标数量可以分为单目标、多目标以及超多目标(目标数量超过4个)优化问题。每个目标的计算方式由目标本身和方案流程决定,服务系统的优化目标通常包括时间、成本、资源利用率、可靠性、资源均衡利用等。式(2)为用户需求中提出的约束,hi(x)≤0表示用户提出的第i个约束,uh为约束数量,不等式中大于和小于可以相互转化,以小于等于代指所有类型约束。式(3)为服务能力约束,cpj(x)为服务方案x中服务模式spj或原子服务sj当前服务能力值,所用服务的服务能力需要大于0。式(4)为顺序约束,约束了服务流程中服务的先后顺序,sspk≻sspl表示服务模式spk或原子服务sk需要在服务模式spl或原子服务sl之前执行。
1.2 问题求解框架
针对服务供需匹配问题,提出如图1所示的求解框架。具体求解环节如下:
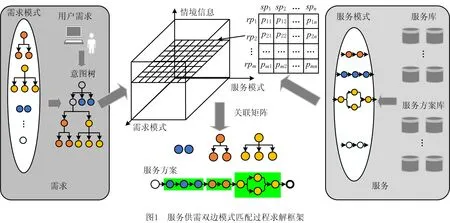
(1)在用户需求端,维护历史需求库,并从中挖掘得到需求模式库。
(2)在服务提供端,维护可用原子服务集,并从历史服务方案中挖掘得到服务模式库。
(3)构建双边模式关联矩阵,利用服务日志中的历史匹配记录,得到需求模式与服务模式间的匹配关系。
(4)构建服务解决方案,针对特定需求,建立需求模型,对用户需求进行匹配,得到一组能够最优匹配所提需求的需求模式。进一步通过关联矩阵找到每个需求模式对应的一组服务模式,针对用户提出的优化目标,适应性地选择优化算法得到匹配的服务模式,最终构造一个满足用户需求的优化服务方案。
其中:环节(1)~(3)为服务方案构造所需基础数据准备阶段,需要维护历史需求库、需求模式库、原子服务库、服务模式库和双边模式关联矩阵;环节(4)为针对特定需求构建服务方案环节。
2 供需双边模式与关联矩阵
2.1 基于意图树的需求模型与需求模式
2.1.1 基于意图树的需求模型
在常用需求建模方法中,面向目标的建模技术因其具有形式直观、易于理解、表达能力强、不需过多专业知识等优点,被广泛应用于需求工程中的需求建模[24,27]。基于目标建模的方法理念,本文提出一种基于意图树的需求模型iTree,
iTree=G,E
其中意图树iTree由意图节点集合G={G1,G2,…,Gn}与意图关联关系集E构成。一个意图树节点Gi包括意图、约束和优化目标,Gi=intension,{constaint},{OptObjective}。意图树节点间的关联关系有分解与依赖两种。需求模型可以由用户直接手工建立,也可以通过其他需求获取的方式建立,如通过与用户对话等方式。
如图2所示为iTree模型中的元素及其关系,详细介绍如下:
(1)User表示用户。
(2)Role表示角色。一个用户可以被分配不同的角色。
(3)Intension表示意图。用户通过意图来描述自己的功能性需求。
(4)Decomposition表示分解。上层意图可以分解为若干下层意图。该关系有“与”和“或”两种。“与”关系表示当下层意图均被满足时,上层意图同时被满足;“或”关系表示当任意一个下级意图能被满足时,上层意图即可被满足。
(5)Dependency表示依赖。同级意图之间某意图的实现依赖于另一意图。
(6)Constraint表示约束。用户通过约束来描述自己的非功能性需求。约束使用键值对定义:Cons=Conskey,Constype,Consvalue,分别表达约束名、约束数据类型和约束值。
(7)OptObjective表示优化目标。用户使用优化目标表达自己的偏好,如解质量优先或求解速度优先,此指标在服务方案构建时予以考虑。
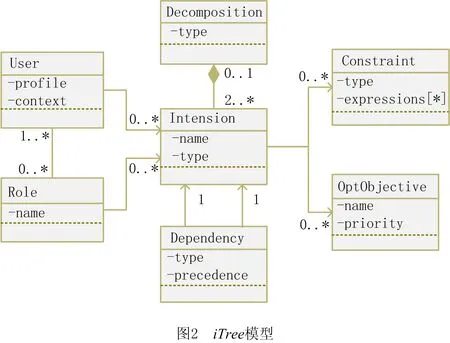
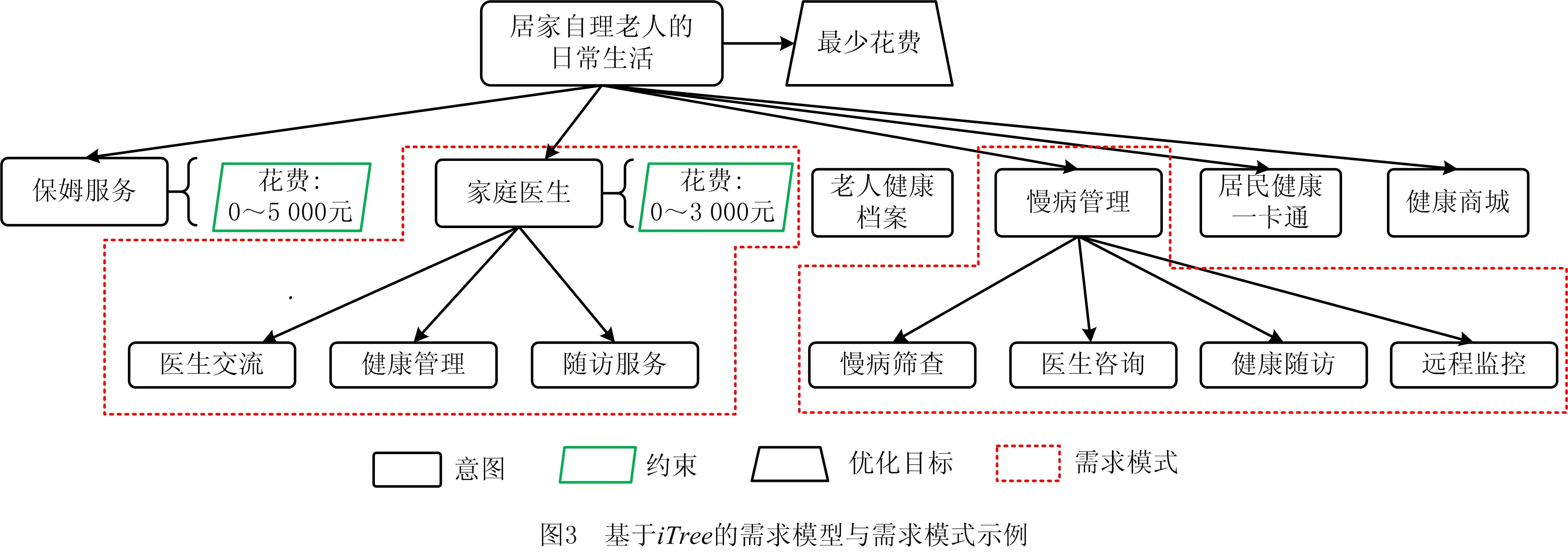
图3给出了一个居家老人日常生活需求的iTree模型实例。老人通过意图树表达自己的日常生活需求:老人需要找一名保姆、找一名家庭医生并进行慢病管理、办理健康档案与居民健康一卡通、使用健康商城服务购买医疗用品。意图树中描述了老人对意图的偏好和非功能性需求,如:老人对服务的偏好是最少花费;在家庭医生服务意图中,老人对非功能性需求进行了指定:花费在0~3 000元间,并进一步表达了自己的需求:需要与医生交流、进行健康管理以及医生随访服务。
2.1.2 基于意图树的需求模式
在大量的用户需求中,某些需求中包含的意图间存在较强的关联性,这些关联意图集往往会在多个需求中被重复提出,这些频繁出现的关联意图集体现了领域用户需求的先验知识,本文对其进行挖掘并刻画为需求模式(RP)。需求模式是对用户需求的模块化描述,在用户需求声明过程中,利用需求模式,通过需求补全、推荐、重构等操作,可将碎片化和不精确的原始需求,快速完整地转换为合理优化的需求。进一步,将需求模式同服务模式关联,形成供需双边模式关联矩阵,增大匹配粒度,提高匹配效率,高效构建服务方案。
基于意图树的需求模式是由多棵子意图树组成的森林,RP=info,{iTreei}。其中:info表示需求模式的基本信息,如需求模式描述和使用频率等;{iTreei}为意图树集合。在图3所示的例子中,存在两个需求模式,一个是“家庭医生服务”,另一个是“慢病管理服务”,其中家庭医生服务需求模式包含了医生交流服务、健康管理服务、随访服务3个频繁出现的子意图以及指定家庭医生服务的约束为花费在0~3 000元间。
需求模式的构建可以采用人工定义和自动挖掘两种手段。自动挖掘包括两个阶段:
第一阶段:频繁意图树结构挖掘。该过程以挖掘频繁树结构为目标,考虑意图与结构,不考虑约束。使用gSpan算法挖掘频繁结构。
第二阶段:需求模式挖掘。从需求全集中提取包含频繁结构的子意图树,根据约束进行聚类,最后得到具有相同结构及意图,但约束不同的需求模式。
由于篇幅限制,本文只简要介绍需求模式挖掘算法思路,详细算法以及如何利用需求模式进行需求的自动补全、推荐、重构等内容将在后续论文进行描述。
2.2 面向关联知识复用的服务模式
在服务互联网环境下,服务之间存在着相似性和关联性,即某些服务之间经常会关联在一起搭配使用,如第1章所述的京东商城和天猫商城的例子。本文对历史服务方案和领域知识中,经常被高频使用的服务流程和服务搭配进行分析和挖掘,形成服务模式(SP)[29]。服务模式定义如下:
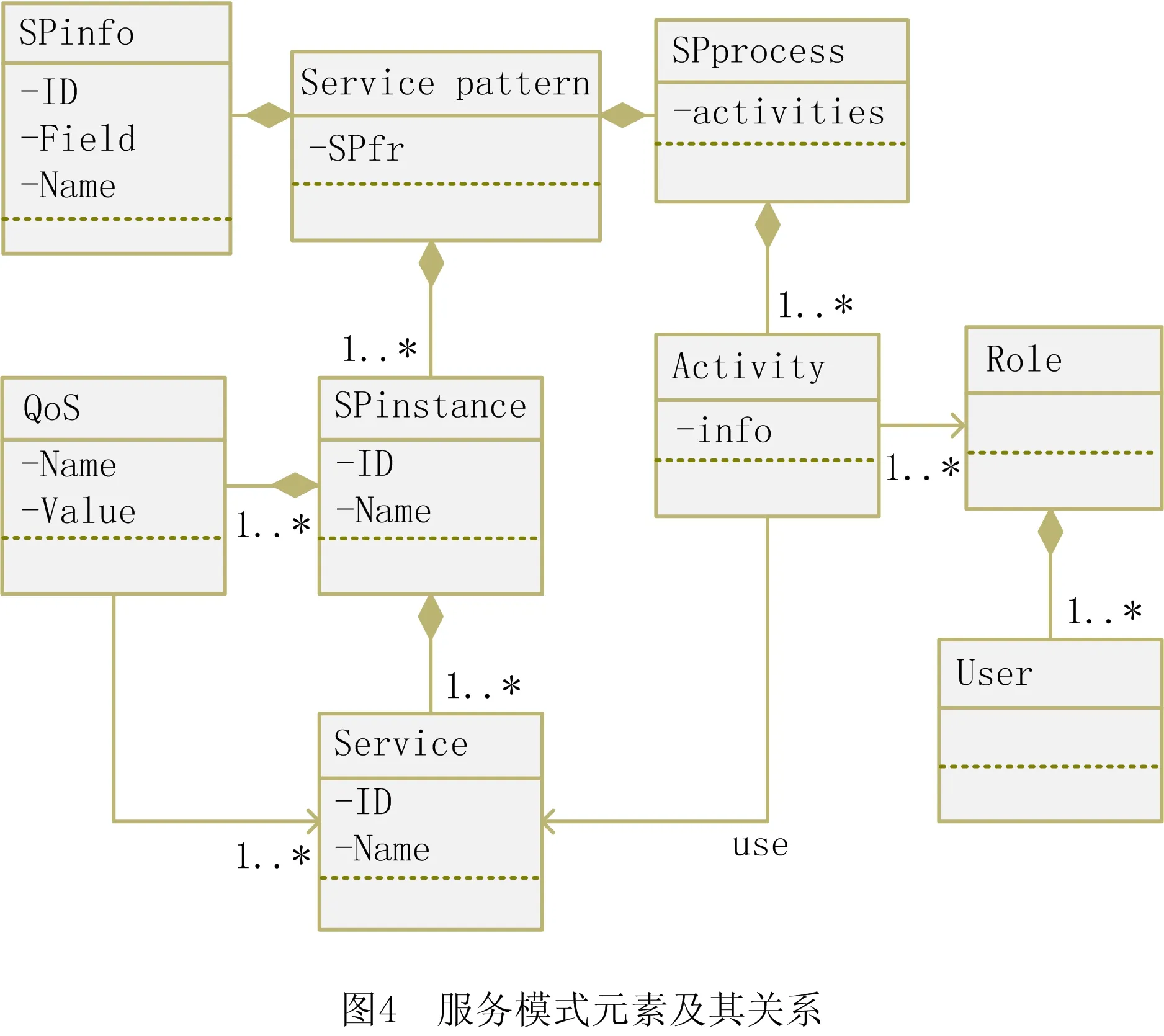
SP=SPinfo,SPfr,SPprocess,SPinstance。
其中:SPinfo表示服务模式的基本信息,如名称、所属领域等;SPfr描述了服务模式完成的功能;SPprocess描述服务流程,实现时可采用业务流程建模与标注(Business Process Modeling Notation, BPMN)格式描述和存储;SPinstance是服务模式的实例集,SPinstance=S,SPQoS,其中:S为该服务模式实例绑定的服务集合,服务可以使用传统的网络服务的本体语言(Ontology Web Language for Services, OWL-S)或Web服务描述语言(Web Services Description Language, WSDL)等服务模型进行建模,SPQoS为服务模式实例的质量指标信息。
如图4所示为服务模式中的元素及其关系。
与利用原子服务构建服务方案相比,服务模式挖掘了历史服务方案中成功的案例并将其重用,减少搜索空间,提高构建效率;此外,由于服务模式体现了领域先验的服务使用知识,可以预先准备建立关联,降低关联成本;且服务模式是经过实践验证的成功案例,可获得更好的用户满意度。
在之前的研究中,已提出采用频繁模式增长(Frequent Pattern growth, FP-growth)算法从服务系统的历史日志中挖掘服务模式[22]。该算法包括两个步骤:利用紧凑的数据结构FP-Tree,对日志进行压缩,避免多次的数据库扫描;使用FP-growth算法挖掘出频繁的服务模式。
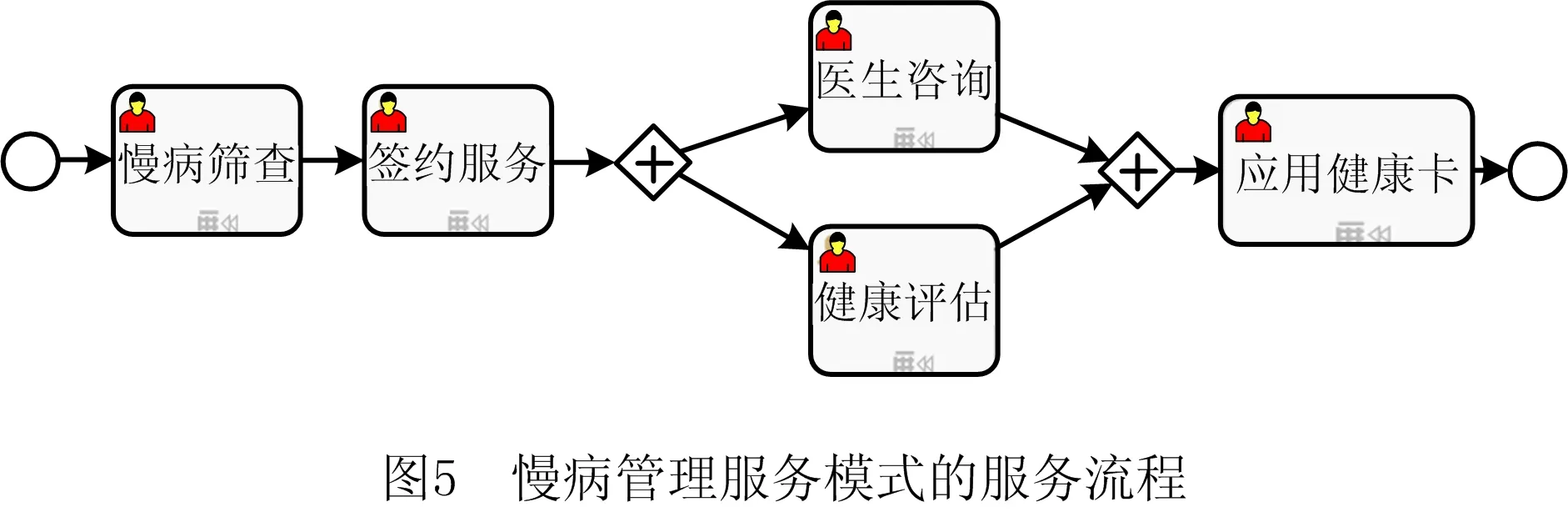
如图5所示的服务模式为一个“慢病管理”服务模式的流程示例,内含5个服务:慢病筛查服务、签约服务、医生咨询服务、健康评估服务和应用健康卡服务。
2.3 供需双边模式关联矩阵
2.3.1 关联矩阵定义
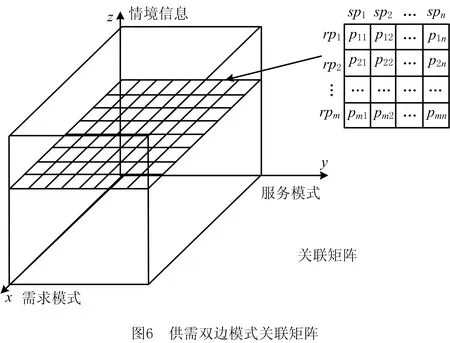
通过2.1节和2.2节介绍的需求模式和服务模式,可以通过固化需求间和服务间的关联关系,形成需求模式和服务模式,通过提升需求与服务的构建单元粒度,缩小搜索空间。可进一步利用历史服务方案中供需双边模式间的成功匹配先验知识,构建双边模式间的多维概率关联矩阵,支持服务方案构建中的快速搜索。该关联矩阵由R,S,RP,SP,Context五个维度构成,其中:R为需求集合,S为服务集合,RP为需求模式集合,SP为服务模式集合,Context为情境信息集合。如图6所示为供需双边模式关联矩阵的示意图,图中:x轴为需求模式,y轴为服务模式,z轴为情境信息。
五个维度间存在多种关联关系,需求模式与服务模式分别蕴含了需求间的关联和服务间的关联,本节重点阐述需求模式与服务模式在不同情境下的关联关系,关联关系的强弱通过匹配度pij∈[0,1)进行度量。
假设共有n个需求模式与m个服务模式,关联矩阵定义如下。
(1)当情境ctk相同时,设需求模式rpi可以匹配mi个服务模式,aij为需求模式rpi与服务模式spj的匹配度。若二者不能匹配,则匹配度aij=0。由于每个需求模式只对应少量服务模式,mi通常远小于m,故需求模式与服务模式之间关系可以表达为稀疏矩阵:
(5)
(2)当同一需求模式rpi所处的用户情境不同时,其对应的服务模式也不同。设有c个情境信息,设bk,j为情境ctk时,需求模式rpi与服务模式spj的匹配度,若二者不能匹配,则匹配度bk,j=0。为简单起见,本文设每个情境信息对应的候选服务模式都有m0个,则相应匹配关系可表达为稀疏矩阵:
(6)
2.3.2 用户情境信息
在不同情境下,同一需求模式能够匹配的服务模式可能不同。因此,在服务方案构建过程中,需要依据服务情境信息的不同,采用不同的策略和优化方法,因此在关联矩阵构建时,要考虑情境维度的信息。
本文所考虑的情境信息包括两类:
(1)用户情境,即用户年龄、性别等自然信息以及用户的职业、人际关系等群体信息。
(2)环境情境,即时间、地点等用户提出需求时所处的环境。
采用键值对形式对情境进行建模,对于连续型情境,使用标准化欧氏距离度量两个情境的相似程度,对于离散型情境,按照one-hot编码规则转换为连续型情境。由于抽象后的情境维度可能过高,本文使用主成分分析法(Principal Component Analysis, PCA)[31]进行降维。
2.3.3 双边模式匹配度计算
双边模式匹配度是需求模式在某情境下匹配服务模式的匹配概率。匹配度的计算需要考虑历史、当前和未来3部分服务数据。因为历史中使用次数较高的服务模式当前可能不会出现,且新需求模式,服务模式对存在冷启动问题,服务模式的约束值也可能会发生变化,所以历史和当前部分数据的匹配度计算需考虑包括时间衰减、约束满足度和匹配次数3个参数。
(1)时间衰减Ti,表示第i次匹配的时间衰减程度,
Ti=1-e-(t0-ti)。
(7)
式中t0表示当前时间,ti表示第i次匹配时间点。
(2)约束满足度Ci,表示第i次匹配时需求模式约束满足程度,
(8)
式中:n为约束数量,cj为第j个约束的服务模式满足度。对于枚举值,满足约束为1,不满足为0;对于范围值的情况,服务模式满足度定义如下:
(9)
式中:wmin与wmax指需求模式中约束的最小值与最大值,w为约束的实际值。
(3)匹配次数记为N。
综合3个参数,包含历史和当前部分信息的匹配度
(10)
未来部分的匹配度pf需要结合特定领域对未来需求与服务的使用情况进行预测,有针对性地调整匹配度。
需求模式中每个子需求的预测值为pf,ri,则需求模式的预测值
其中:n为子需求的个数;ai为子需求i的权值,本文认为需求模式中约束多的子需求为更重要的部分,在匹配度计算中权值越大,因此ai为子需求i约束的数量。同理,服务模式的预测值pf,s即为每个服务预测值的平均值。在实际应用中,可根据使用具体情境,采用对应的预测模型,获得需求和服务的变化趋势,设计预测值pf,ri的计算方法。综上,包含历史、当前和未来3个部分信息的匹配度
(11)
其中,由于历史和当前部分可以同时考虑,统一用k1表示历史和当前部分的权重;k2表示将来部分的权重,k2的大小与需求和服务预测的置信度有关,预测的置信度越低,k2越小。
将p归一化即为最后得到的匹配度。
关联矩阵在使用时,首先通过用户情境信息找到Ak,再根据需求模式找到与其对应的服务模式集,经过优化得到最终的服务方案。如图3的需求模型,用户提出居家老人的日常生活意图树,假设其情境信息的一部分为60岁,哈尔滨,则根据其情境信息,就只会找到适合60岁且地点在哈尔滨的家庭医生和慢病管理的服务模式。
2.4 供需双边模式关联矩阵的构建与更新方法
2.4.1 供需双边模式关联矩阵的构建算法
算法1双边模式关联矩阵构建算法。
输入:服务方案集合solution;
输出:关联矩阵A。
1 begin
2 用户情境集合X=∅;匹配时间点集合D=∅;关联矩阵A=∅
3 foreach服务方案si∈solution do
4 foreach (rpj,spk)∈sido
/* X[(rpj,spk)]与D[(rpj,spk)]初始为空列表*/
5 X[(rpj,spk)]←X[(rpj,spk)]+ci//ci为si中用户情境
6 D[(rpj,spk)]←D[(rpj,spk)]+ti//ti为si中匹配时间点
7 end
8 end
9 foreach (rpj,spk)∈X do
10 Cij←X[(rpj,spk)]
11 Tij←D[(rpj,spk)]
12 使用PCA算法对Cij降维
13 使用Birch算法对Cij聚类
14 计算匹配度,并将聚类结果与匹配度加入A中
15 end
16 返回A
17 end
2.4.2 供需双边模式关联矩阵的更新策略
由实验可知,当服务日志中总方案数量很多时,更新时间会达到1个小时甚至更多,关联矩阵更新代价巨大。因此,需要根据总服务方案数量动态调整更新频率,在更新效率与更新效果间进行均衡。本节根据关联矩阵的特点针对性地提出了关联矩阵的适应性更新策略,关联矩阵在满足一定条件时进行更新,以实时调整关联矩阵的内容。
(1)新增策略 该策略包含两部分:

2)增加新的需求模式,服务模式。此时,在服务日志中找到新增模式的匹配情况,并更新关联矩阵。
(3)服务质量变化策略 服务质量发生变化会导致匹配度中约束满足度发生变化,这时也需要对关联矩阵中的匹配度进行更新。
在关联矩阵使用时,需定期判断是否满足上述策略。如满足策略1或策略2,使用算法2对关联矩阵进行更新;如满足策略3,对使用该服务的需求模式,服务模式对的匹配度进行更新。当需求模式,服务模式对在某情境下的匹配度降低到某一阈值时,在匹配中不予考虑,视为该对失效,但在关联矩阵中保留数据,随关联矩阵进行更新。
双边模式关联矩阵的更新算法如算法2所示,从历史记录中取出需要更新的需求模式,服务模式对,读取其PCA模型与Birch模型,将新的匹配记录加入模型中并计算匹配度。
算法2双边模式关联矩阵更新算法。
输出:更新后的关联矩阵A。
1 begin
2 用户情境X′=∅;匹配时间点D′=∅
3 foreach服务方案si∈solution do
4 foreach(rpj,spk)∈sido
/* X′[(rpj,spk)]与D′[(rpj,spk)]初始为空列表*/
5 if(rpj,spk)∈rpsp and匹配时间点大于上次更新时间do
6 X′[(rpj,spk)]←X′[(rpj,spk)]+ci//ci为si中用户情境
7 D′[(rpj,spk)]←D′[(rpj,spk)]+ti//ti为si中匹配时间点
8 end
9 end
10 foreach (rpj,spk)∈X′ do
13 if (rpi,spj)∉X do
16 end else
17 Cij←X[(rpj,spk)]
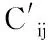
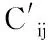
20 计算匹配度,并将聚类结果与匹配度加入A中
21 end
22 返回A
23 end
3 基于供需双边模式的服务方案构建算法
服务方案构建算法的目标是获得优化的服务执行方案Solution,
Solution=Info,SSP,Process,Q。
其中:Info为基本信息;SSP为方案中使用的服务模式SP与原子服务集合S;Process为服务流程;Q为质量指标。如图1所示,构建算法流程分为需求匹配、服务模式与原子服务选择、生成服务流程3个步骤。
3.1 需求匹配方法
需求匹配的目标是利用历史需求信息,使用需求模式去覆盖意图树的过程。其结果包含可被需求模式匹配的意图集(体现为对应的需求模式集)和不能被匹配的意图集两部分。
匹配算法采用基于优先规则的迭代方式,逐步使用需求模式覆盖意图树中未被覆盖的意图,即使需求模式中包含的意图和需求树中待匹配意图完全相同,且需求模式中的约束包含待匹配意图的约束。
需求匹配优先规则的顺序如下:
(1)优先考虑覆盖率更高的匹配方案;
(2)优先考虑使用更少需求模式的匹配方案;
(3)优先考虑需求模式平均使用频率更高的匹配方案。
限于篇幅,匹配算法流程不再赘述。
3.2 构建服务方案
在得到需求模式集和单独的意图集之后,该环节基于双边模式关联矩阵和服务的描述信息,利用算法得到优化后的服务方案。
构建步骤分为以下两个部分:
(1)对需求进行需求匹配。根据需求匹配的结果和匹配情境,从关联矩阵中找到与各需求模式对应的匹配度较高的服务模式集,并在服务库中找到与各单独意图对应服务功能的服务集。如果某需求模式找不到对应的服务模式,则对该需求模式利用更小粒度的需求模式进行需求匹配,并重复以上步骤。
(2) 在上述集合当中选择合适的服务模式和服务,并构建服务流程。利用匹配算法,最终得到满足约束且优化目标最优的服务方案。
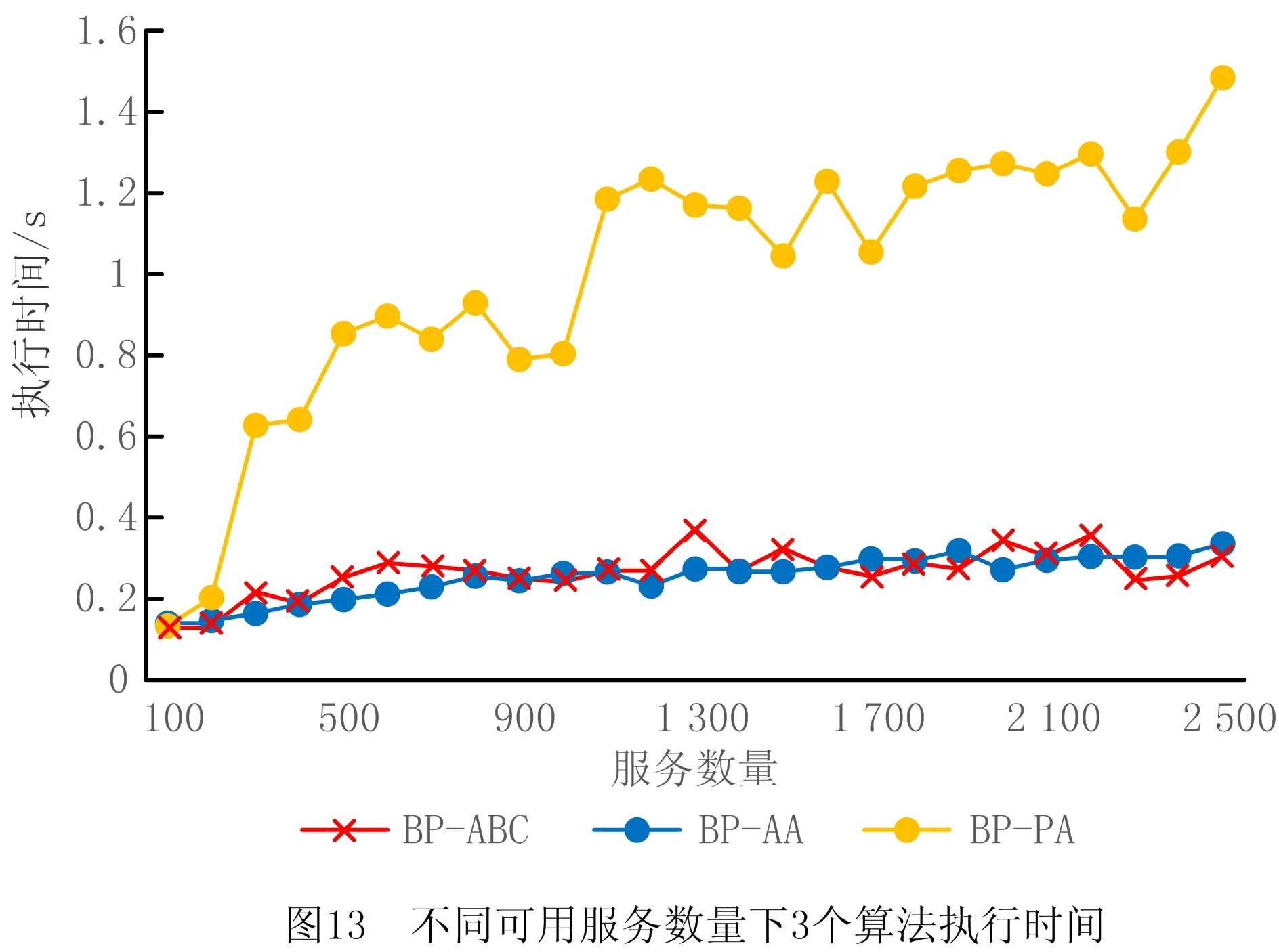
由于在不同实际应用场景中,服务数量和需求数量规模不同,追求的质量与效率的偏好不同,因此,本文提出3类算法,并将双边模式以及关联矩阵融入其中:精确算法(Bilateral Pattern Precise Algorithm, BP-PA),适用于数据规模较小且用户需要最优解的场景;贪心算法(Bilateral Pattern Approximation Algorithm, BP-AA),适用于数据规模适中且用户对算法效率要求较高的场景;人工蜂群算法(Bilateral Pattern Artificial Bee Colony Algorithm, BP-ABC),适用于数据规模较大且用户需要质量较好解的场景。
BP-PA算法通过遍历每个服务方案来获得最优解,在实际应用中通常使用各种不同的剪枝算法来提高运行速度,如:若当前遍历的部分服务方案已经劣于当前最优方案,不再继续对该部分服务方案的后续服务进行遍历等。

BP-ABC算法(算法5)使用的可行性准则定义如下:如果解x1和解x2满足以下3点之一,则称解x1支配解x2:①解x1满足约束而解x2不满足约束;②解x1和解x2均不满足约束,但x1总约束满足度较大;③解x1和解x2均满足约束,但解x1帕累托支配解x2。
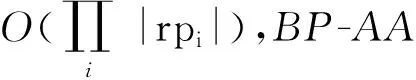
算法3精确算法(BP-PA)。
输入:用户意图树iTree,需求模式集RP,服务模式集SP和原子服务集S,关联矩阵A,用户需求情境ctk;
输出:最优服务方案x*。
1 begin
2 x*←∅
3 调用需求匹配算子reqMatch,利用RP覆盖iTree,获得需求匹配结果:需求模式集RP′,未能匹配的意图集R′(见3.1节)。
4 从A中根据ctk找到子矩阵Ak并根据RP′中各rpi找到对应的服务模式集SPi,在S中找到R′中意图rj与服务功能对应的服务集Sj。
5 对SPi中服务模式以及Sj中原子服务按照优化目标排序
6 foreach服务模式spim∈SPi与原子服务sjn∈Sjdo
7 调用服务流程构建算子constructingProcess获得服务方案x
8 if x满足约束且优化目标优于x*
9 x*←x
10 end else continue
11 end
12 返回x*
13 end
算法4贪心算法(BP-AA)。
输入:用户意图树iTree,需求模式集RP,服务模式集SP和原子服务集S,关联矩阵A,用户需求情境ctk;
输出:最优服务方案x*。
1 begin
2 x*←∅; success←0; i←0;初始化循环次数N
3 调用需求匹配算子reqMatch,利用RP覆盖iTree,获得需求匹配结果:需求模式集RP′,未能匹配的意图集R′(见3.1节)。
4 从A中根据ck找到子矩阵Ak并根据RP′各rpi找到对应的服务模式集SPi,在S中找到R′中意图rj与服务功能对应的服务集Sj。
5 对SPi中服务模式以及Sj中原子服务按照优化目标排序
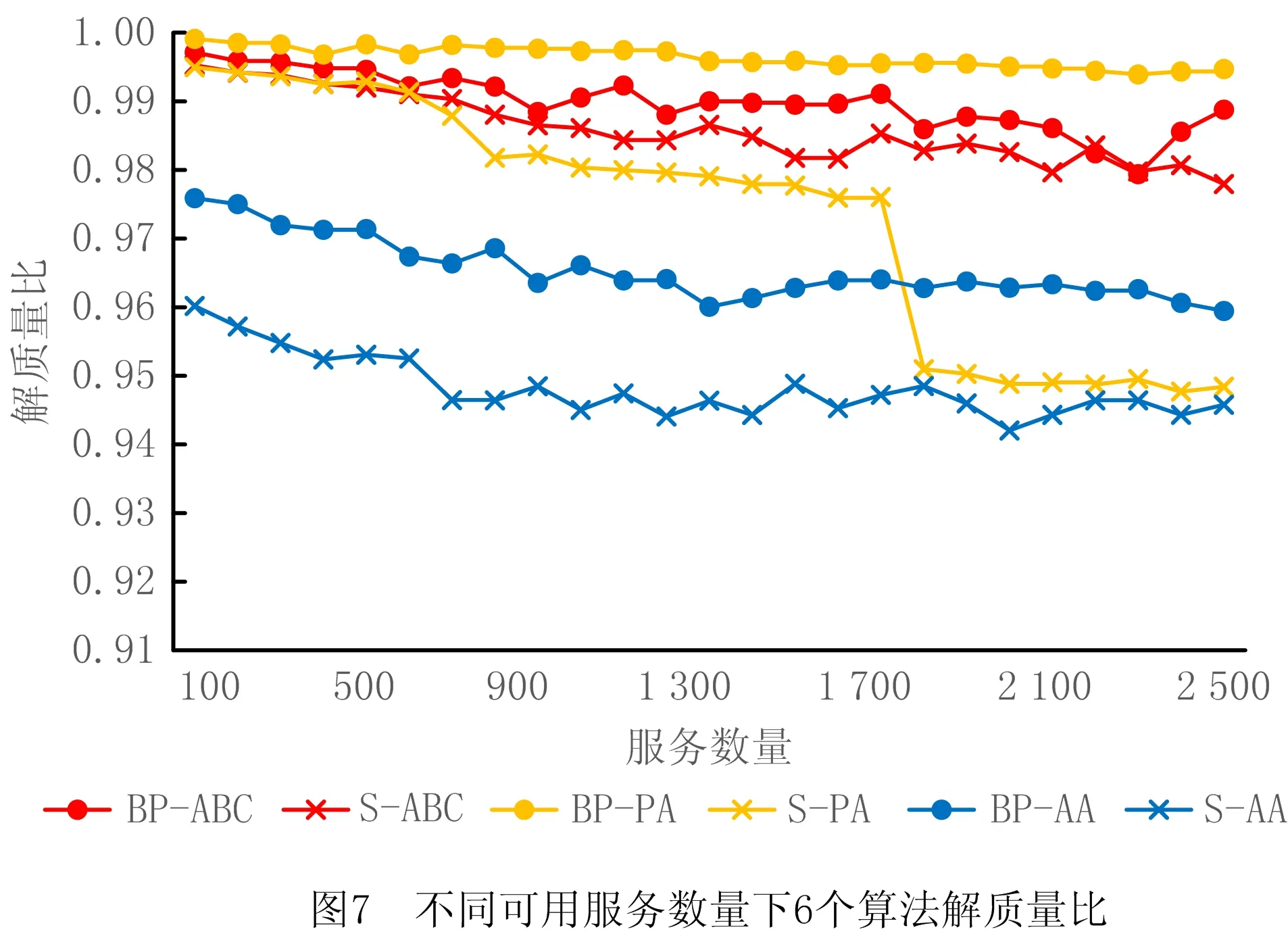
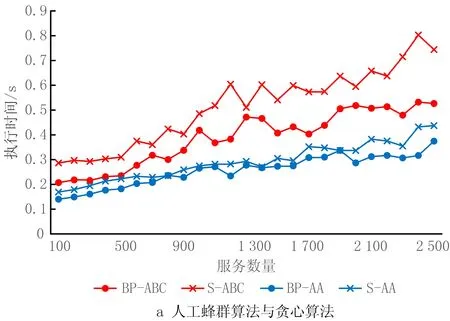
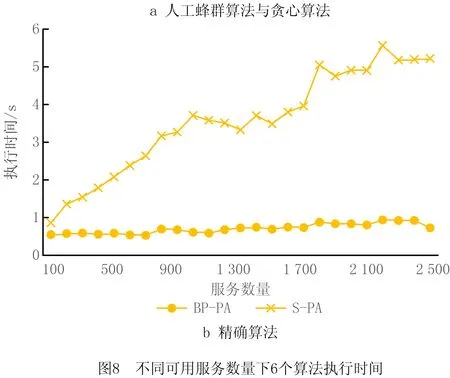
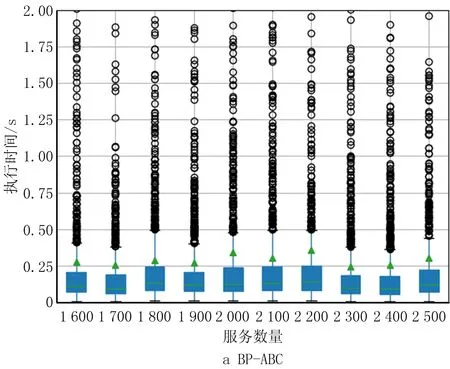
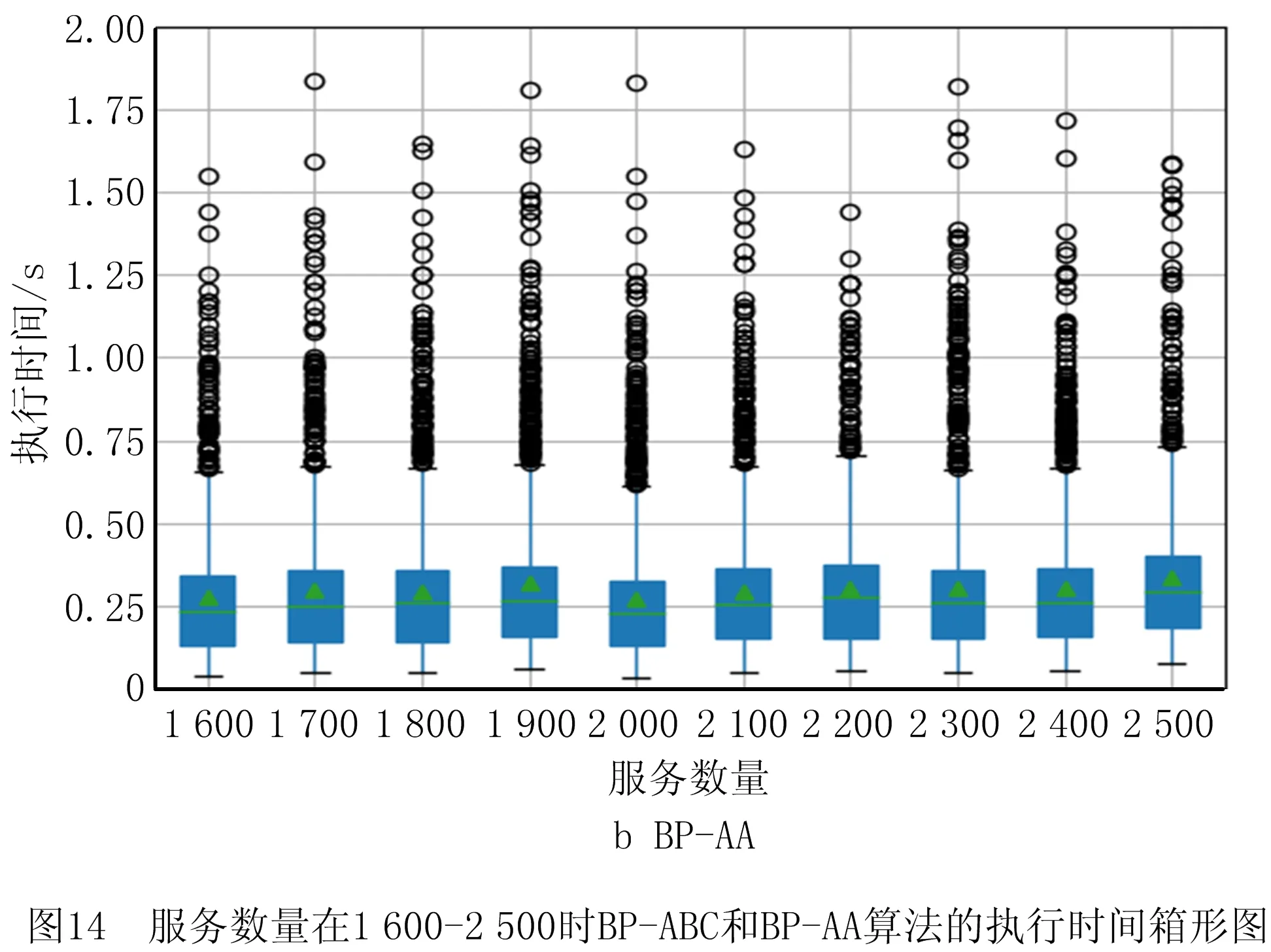
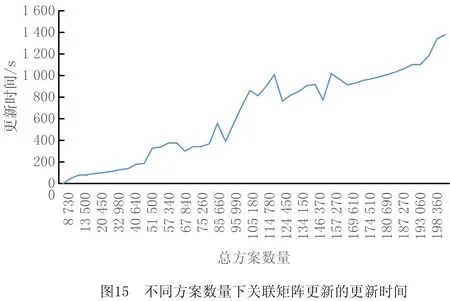
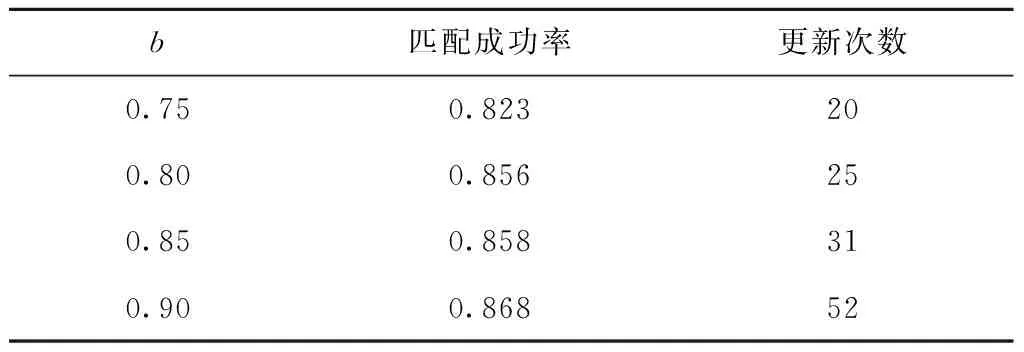
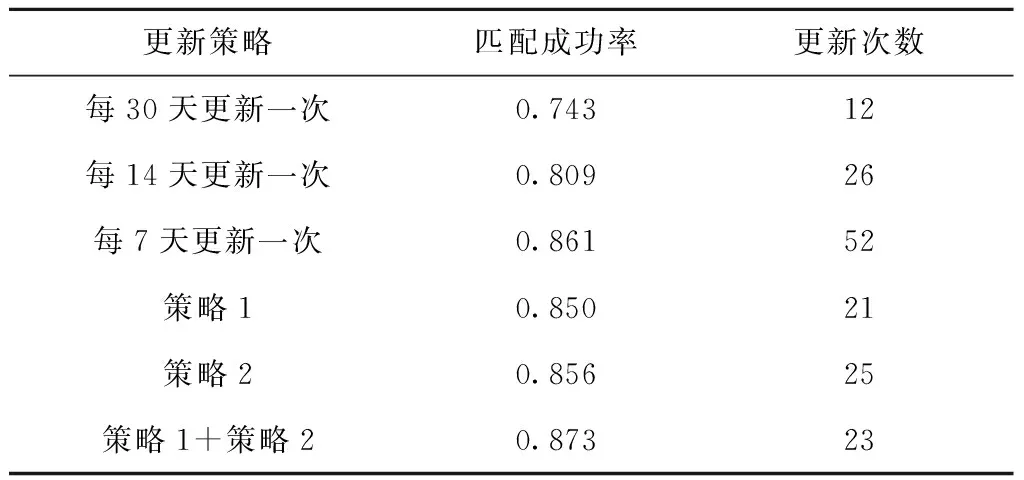
6 while success=0 and i 7 根据贪心准则选择服务模式进行替换 8 调用服务流程算子buildingProcess获得服务方案x* 9 i←i+1 10 if x*满足约束 11 success←1 12 end else continue 13 end 14 返回x* 15 end 算法5人工蜂群算法(BP-ABC)。 输入:用户意图树iTree,需求模式集RP,服务模式集SP和原子服务集S,关联矩阵A,用户需求情境ctk; 输出:最优服务方案x*。 1 begin 2 x*←∅;j←0;初始化循环次数MCN;侦察蜂参数limit;食物源个数SN;跟随蜂个数d 3 调用需求匹配算子reqMatch,利用RP覆盖iTree,获得需求匹配结果:需求模式集RP′,未能匹配的意图集R′(见3.1节)。 4 从A中根据ck找到子矩阵Ak并根据RP′各rpi找到对应的服务模式集SPi,在S中找到R′中意图rj与服务功能对应的服务集Sj。 5 根据SPi与Sj随机生成SN个服务方案xi 6 foreach j 7 foreach xido 8 随机选择xi中1维用其他服务模式替换。 11 counti←0 12 end else counti←counti+1 13 随机选择d个服务方案,使用NSGA Ⅱ多目标优化法优化 14 foreach xido 15 if counti>limit do 16 随机生成服务方案xi 17 end else continue 18 end 19 记录当前最优的服务方案x*;j←j+1 20 end 21 返回x* 22 end 本节介绍将选择后的服务模式和原子服务构造成一个流程的方法。在服务方案历史执行流程中对每个服务模式和服务加上时间戳,用来记录服务与服务模式间的执行顺序。顺序执行的服务/服务模式,时间戳依次加1,并行执行的,时间戳相同。 若将P中的服务模式和服务表示为图中的点,大于1的值表示为图中的边,可以将P表示成一张有向图。因为P中服务模式间的偏序关系可能存在环,所以使用贪心算法去掉环,使用的贪心策略为:去掉Σpij最大的spi的入边。去环后的P即为一个合理的服务流程。服务流程构建算子constructingProcess如算法6所示。 算法6服务流程构建算子constructingProcess。 输入:服务模式集SP,服务集S,顺序比矩阵P; 输出:服务流程s*。 1 begin 2 t←0;SP′←SP+S;ti←0为各服务模式/服务的时间戳 3 while SP′≠∅ do 4 foreach spi∈SP′ and spj∈SP′ do 5 si←0 6 if pij<1 do 7 si←si+1 8 end 9 end 10 将si最小的spi放入集合SP″中,s←minsi 11 if s=0 do 12 foreach spi∈SP″ do 13 ti←t 14 SP′←SP′SP″ 15 end else 16 foreach spi∈SP″ and spj∈SP′ do 17 spm←Σpij最大的服务模式 18 if pmj<1 do 19 pmj←1; pjm←1 20 end 21 SP′←SP′{spm} 22 end 23 t←t+1 24 end 25 返回依据时间戳升序原则生成的服务流程s* 26 end 本章将对所设计的基于双边模式的3个服务方案构建算法进行实验分析,并与对应不采用模式的传统算法进行比较。此外,对所提双边模式关联矩阵的更新策略进行实验,分析其有效性。 本文选择公开服务数据集CrossWOZ[32]作为实验数据集,CrossWOZ是一个大规模的中文跨领域数据集。它包含5个领域的6 012个需求对话及相关服务资源,服务资源包括:酒店、餐厅、景点、地铁和出租车5大类。下面是数据集提供的一条需求对话示例。 CrossWOZ usr:你好,可以帮我推荐一个评分是4.5分以上的景点吗? Hello, could you recommend an attraction with a rating of 4.5 or higher? sys:天安门城楼,簋街小吃和北京欢乐谷都是很不错的地方呢。 Tiananmen, Gui Street, andBeiJjing Happy Velleyare very nice places. usr:我喜欢北京欢乐谷,你知道这个景点周边的酒店都是什么吗? I likeBeijing Happy Valley. What hotels are around this attrraction? sys:那可多了,有A酒店,B酒店,C酒店。 There are many, such as hotel A, hotel B, and hotel C. usr:太好了,我正打算在景点附近找个酒店住宿呢,知道哪家评分是4分以上,提供叫醒服务的不? Great! I am planning to find a hotel to stay near the attraction. Which one has a rating of 4 or higher and offers wake-up call service? 针对本文所提方法的特点,对数据作以下处理,以形成服务、服务模式、需求、需求模式和双边模式关联矩阵等实验数据: (1)将数据集中的对话转化为意图树作为需求数据,共6 012棵意图树;数据集中服务资源作为可用服务,为增加可用服务规模,以验证算法的求解效率,增加华为应用商店中评分较高的地图与天气预报服务,共2 569个服务。 (2)随机选取1 000棵意图树作为训练集,挖掘得到需求模式集;从训练集中生成对应服务方案集,从中挖掘得到服务模式集。 (3)对所选的1 000棵意图树形成的训练集进行需求模式与需求的匹配,根据匹配结果中包含的需求模式在服务方案中对应的服务模式,构造双边模式关联矩阵。 对BP-PA、BP-AA、BP-ABC三个本文所提出的基于双边模式的服务方案构造算法,以及S-PA、S-AA、S-ABC三个对应的不使用双边模式的算法进行对比。将CrossWOZ数据集中除1 000条训练集之外的其余5 012条数据作为验证集,从可用服务数量、需求复杂度(所含意图的数量)、双边模式关联矩阵在匹配中可用程度(通过需求模式对需求的覆盖程度来度量)3方面输入数据的变化进行实验分析,用算法执行时间和解质量两个指标进行对比。其中解质量指标采用当前对比算法所得解同最优解的比值(解质量比)度量,如式(12)所示: (12) 为公平对比,进行解质量比对比时,BP-PA和S-PA算法所生成服务方案的解质量比是在执行时间8 s下获得;BP-ABC和S-ABC算法所生成服务方案的解质量比是在执行时间0.5 s下获得;BP-AA和S-AA算法的解质量比的获得没有时间限制。 进行执行时间对比时,BP-PA和S-PA算法的执行时间是在所生成服务方案的解质量比为0.95的前提下获得;BP-ABC和S-ABC算法的执行时间是在所生成服务方案的解质量比为0.98的前提下获得;BP-AA和S-AA算法的执行时间没有解质量比限制。 针对S-ABC和BP-ABC算法,运行10次,取平均值。 (1)不同可用服务数量下实验结果 本节在可用服务数量为100~2 500时对6个算法进行对比,以验证各算法在不同可用服务数据规模下的求解速度和求解质量,结果如图7与图8所示。由于执行时间数据差异较大,为了能够清晰地加以区分,将2个精确算法的执行时间单独列出。 由图7与图8可见,无论是解质量还是算法效率,使用双边模式下均优于不使用双边模式,且服务数量越多,数据规模越大,使用双边模式的表现越好。由于数据的关系,在服务数量为1 800时,不使用双边模式的精确算法的解质量比发生突变,这是因为在该范围内出现了一个质量较好的服务,但是由于执行时间被限制在8 s,导致精确算法并没有搜索到该服务就已经停止。由于其他算法能搜索到该服务,故此点为异常点。 (2)不同意图树节点数量下实验结果 本节在意图树节点数量为2~7时对6种算法进行实验,以验证各算法在不同需求复杂程度下的求解速度和求解质量,结果如图9与图10所示。 从图9和图10可见,无论是解质量还是算法效率,使用双边模式的算法均优于不使用双边模式,且意图树节点数量越多,需求越复杂,使用双边模式的表现越好。观察不使用双边模式的人工蜂群算法在解质量比的表现,可以发现在意图树节点数量在7时发生突变,原因是运行时间0.5 s不足以让算法收敛,得到满意的解。 (3)不同需求模式覆盖比例下实验结果 本节在需求模式覆盖比例不同时对6种算法进行实验,以验证各算法在关联矩阵的可用程度不同时的求解速度和求解质量。如实验(2)所示,由于意图树规模对实验结果有较大影响,选择使用节点数量为5的意图树作为实验集,结果如图11与图12所示。 如图11与图12所示,在解质量方面,使用双边模式的算法要优于不使用双边模式的算法,且需求模式覆盖比例越高,使用双边模式的算法解质量比越好。在算法效率方面,当需求模式覆盖比例为0(关联矩阵不发挥作用)时,使用双边模式的算法退化为不使用双边模式的算法,由于使用双边模式的算法需要进行需求匹配,算法执行时间要多于不使用双边模式的算法,随着需求模式覆盖比例的增加,使用双边模式的算法在匹配效率方面逐渐优于不使用双边模式的算法。 (4)3种求解策略对比 本实验中BP-PA和BP-ABC算法的执行时间是在所生成服务方案的解质量比为0.97的前提下获得的,实验结果如图13所示。当服务规模较小(100~200),在获得近似解质量比的情况下,3个算法的时间差距不大(0.1~0.25 s),因此选择BP-PA算法以得到最优的解质量比;在服务规模中等(300~1 500)时,BP-PA算法执行时间较长(0.5~1.25 s),而BP-ABC算法求解时间较BP-AA算法长,因此选择BP-AA算法平衡算法速度与解质量;在服务规模较大(1 600~2 500)时,BP-ABC和BP-AA的求解速度相互起伏,无法通过平均时间判定算法优劣,因此本文对服务数量在1 600~2 500,BP-ABC和BP-AA两个算法的箱形图(如图14)进行分析。 对两组数据进行t检验,结果如表1所示。 表1 服务数量在1 600~2 500时BP-ABC和BP-AA算法的执行时间t检验 由于样本数量大,本文选择显著度水平α=0.025,当p<α时,拒绝零假设,即有显著差异。当服务数量为2 300时,两组数据均值有显著差异,这时BP-ABC的均值为0.245,BP-AA的均值为0.303,前者的平均执行时间要少于后者。对于其他服务数量,均值无显著差异,而BP-ABC的矩形箱明显偏下,大部分需求的执行时间优于BP-AA,因此优先选择BP-ABC提升求解速度。 首先对使用关联矩阵更新策略的必要性进行验证。实验内容为当总服务方案数量在0~200 000时更新关联矩阵并记录执行时间,结果如图15所示。 由实验可知,更新时间与总方案数量基本呈线性关系,当日志中的方案数量为25 000时,更新时间为125 s,但当方案数量很大时(超过175 000),日志中方案不断累积,更新时间会达到1 000 s甚至更多,关联矩阵更新代价巨大。由此可见,有必要对关联矩阵采用动态更新频率和策略。 下面对关联矩阵更新策略的有效性进行验证。由于数据集中没有时间信息,本文通过百度指数网站收集2019年各景区逐日网络关注度数据来模拟一年中各景区每日的访问量,模拟每日各需求出现的数量。首先使用精确算法生成最优解并挖掘服务模式,再根据精确解中的每个景区,得到对应需求每日被提出的次数。因为数据中没有服务QoS变化的信息,所以本文不对策略3进行实验验证。本文假设每次更新的总方案数量相同。如2.4.2节所述,当某需求模式,服务模式对在某情境下的匹配度降低到一定程度时,在匹配中不予考虑,且4.2节已经通过实验证明使用双边模式生成服务方案在效率和匹配质量上要优于不使用双边模式,所以本节以匹配成功率和更新的次数来度量更新策略的效果,匹配成功率越高,更新次数越少,策略越优。 (1)策略1:新增策略 本节对策略1的参数a进行分析,结果如表2所示。可以发现,随着参数a的降低,匹配成功率增大,更新次数增多,但是当a过小时,更新次数迅速增加但匹配成功率变化不大,策略效果达到瓶颈。综合考虑,本文选择a=0.1作为策略1的参数。 表2 策略1参数设置 (2)策略2:突变策略 对策略2的参数b进行分析,结果如表3所示。可以发现,随着b的增大,匹配成功率增大,更新次数增多。与参数a相似,当b过大时,更新次数迅速增加但是匹配成功率变化不大。综合考虑,本文选择b=0.8作为策略2的参数。 表3 策略2参数设置 (3)同时考虑两种更新策略 如表4的4~6行所示,同时使用两种策略比仅使用一种策略的匹配成功率高,且更新次数相近,说明同时使用两种策略要优于单独使用一种策略。观察表的前3行与后3行,可以发现定期更新策略要劣于使用本文提出的关联矩阵更新策略。因此,本文提出的关联矩阵更新策略在匹配成功率与更新次数上表现较优,在关联矩阵使用过程中有较好的效果。 表4 关联矩阵更新策略实验验证 针对服务互联网中的服务供需匹配这类复杂优化问题,本文基于模块化的思想提出了基于供需双边模式的服务匹配问题模型。当服务日志中已经存在了一定的历史服务方案,利用领域先验知识挖掘需求模式与服务模式,增加匹配粒度,提高重用效率。设计多维关联矩阵建立需求模式和服务模式的关系,提出自适应关联矩阵更新策略动态调整更新频率,进一步提高匹配效率。针对3种不同场景设计3种算法构建服务方案,通过对各算法的求解质量与执行时间的对比,证明所提的使用双边模式的算法(以S-ABC算法与BP-ABC为例)在时间上提高了41.2%,在质量上提高了1.12%。通过对关联矩阵更新策略的匹配成功率与更新次数的对比,证明本文提出的关联矩阵自适应更新策略(与每14天更新作比较)在匹配成功率上提高了7.9%。 在未来工作中,将进一步研究关联矩阵的多维数学模型建模,优化存储和查询的数据结构,索引技术等内容,提升检索效率,降低存储空间,解决矩阵稀疏性等问题。同时,考虑将方法扩展至分布式环境中,需求与需求模式、服务与服务模式以及关联矩阵将如何存储,节点间应以何种策略协作以完成全局目标构建优化的服务解决方案将是今后的研究重点。
3.3 生成服务流程

4 实验与分析
4.1 实验环境
4.2 基于双边模式的服务方案构建算法的实验与分析
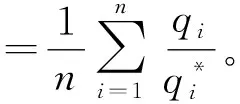
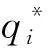
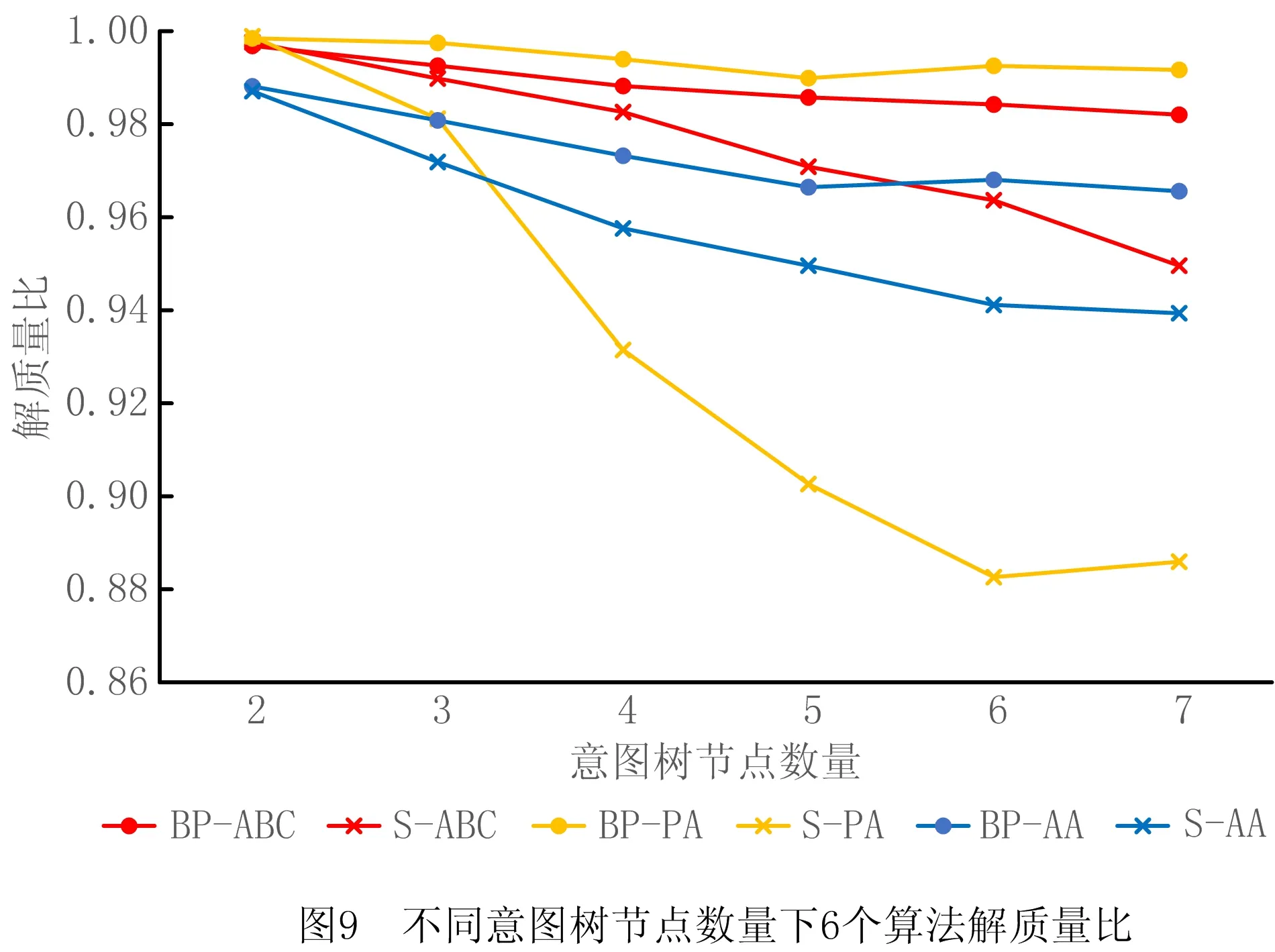
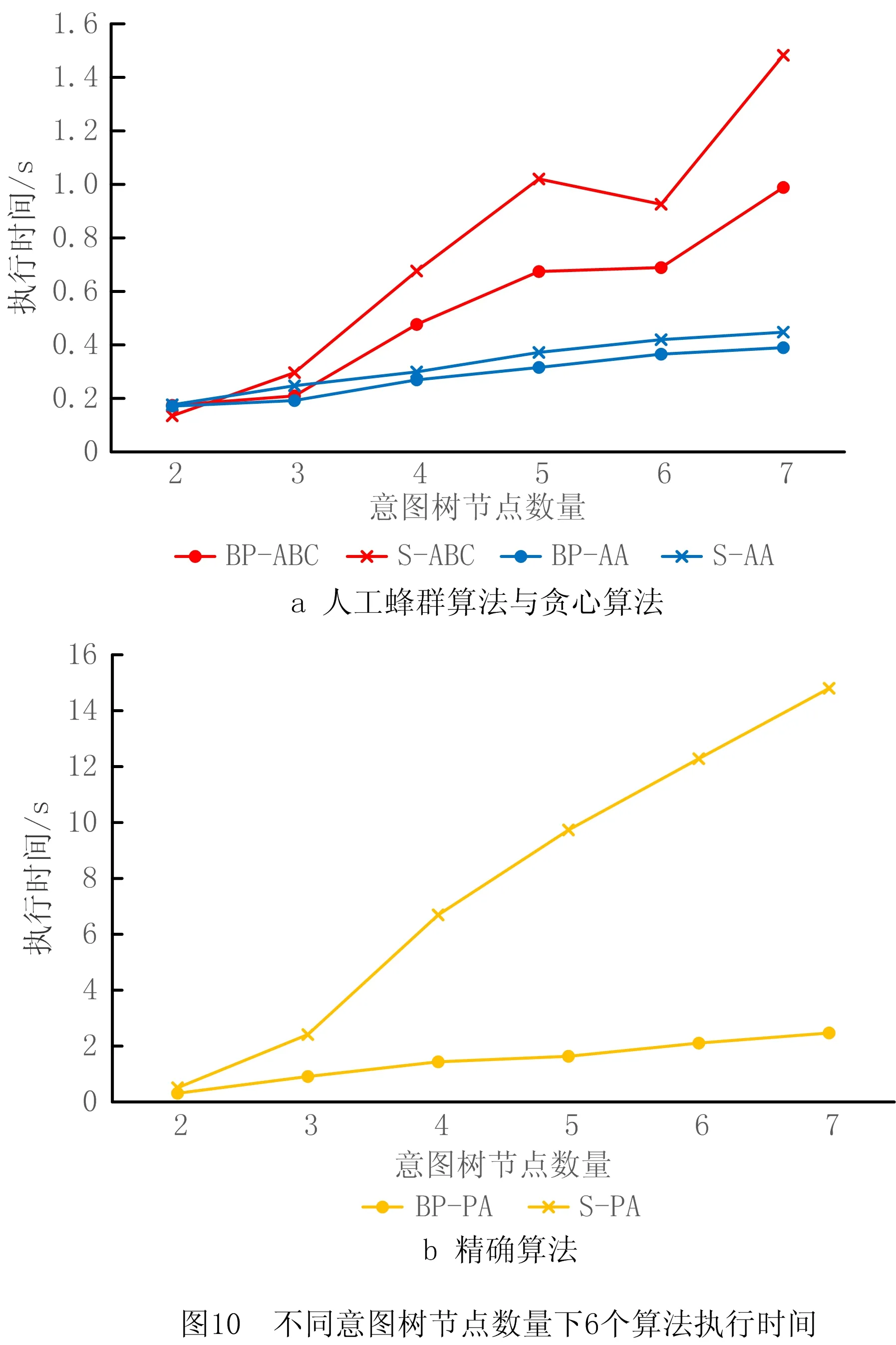
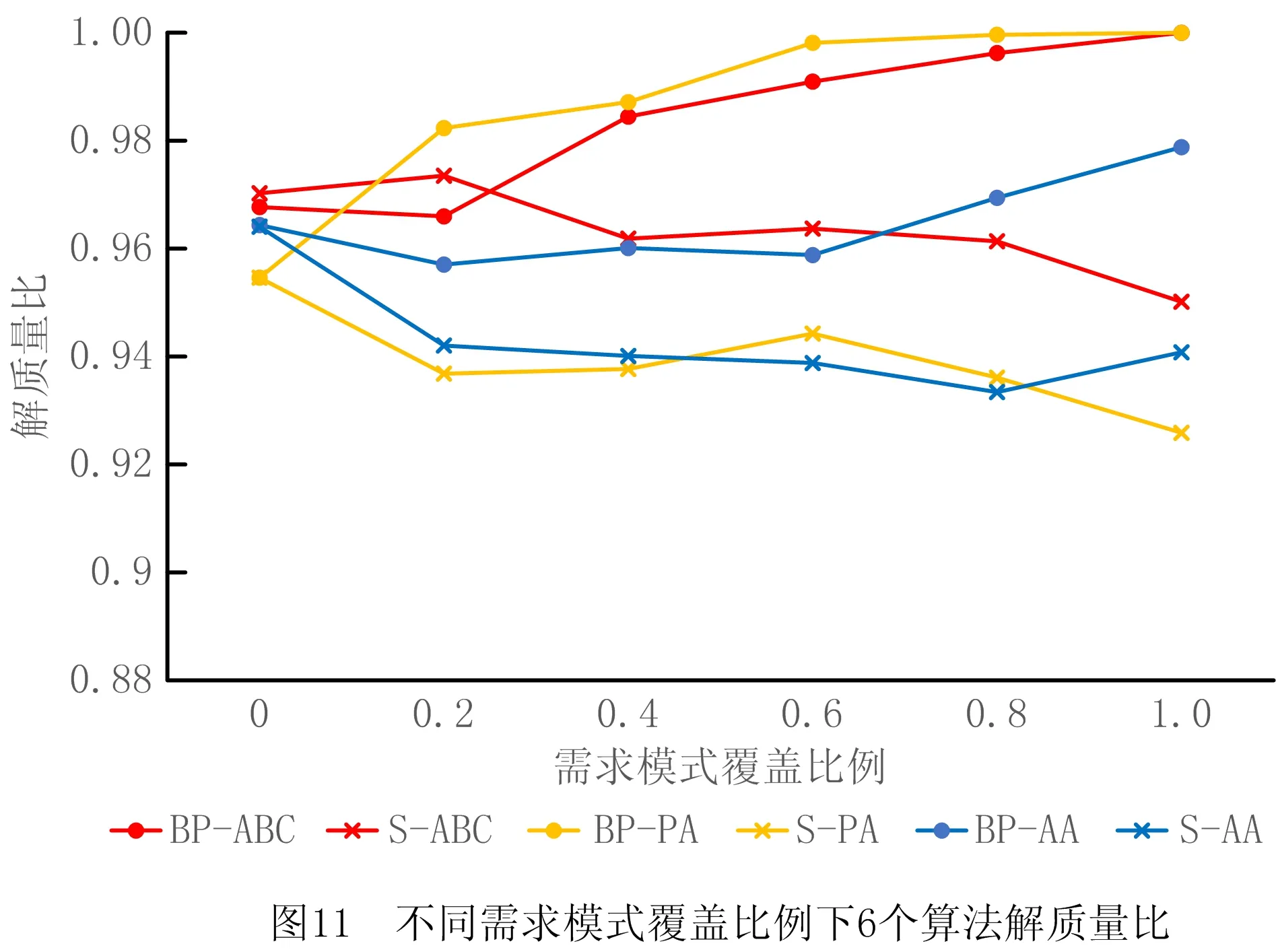
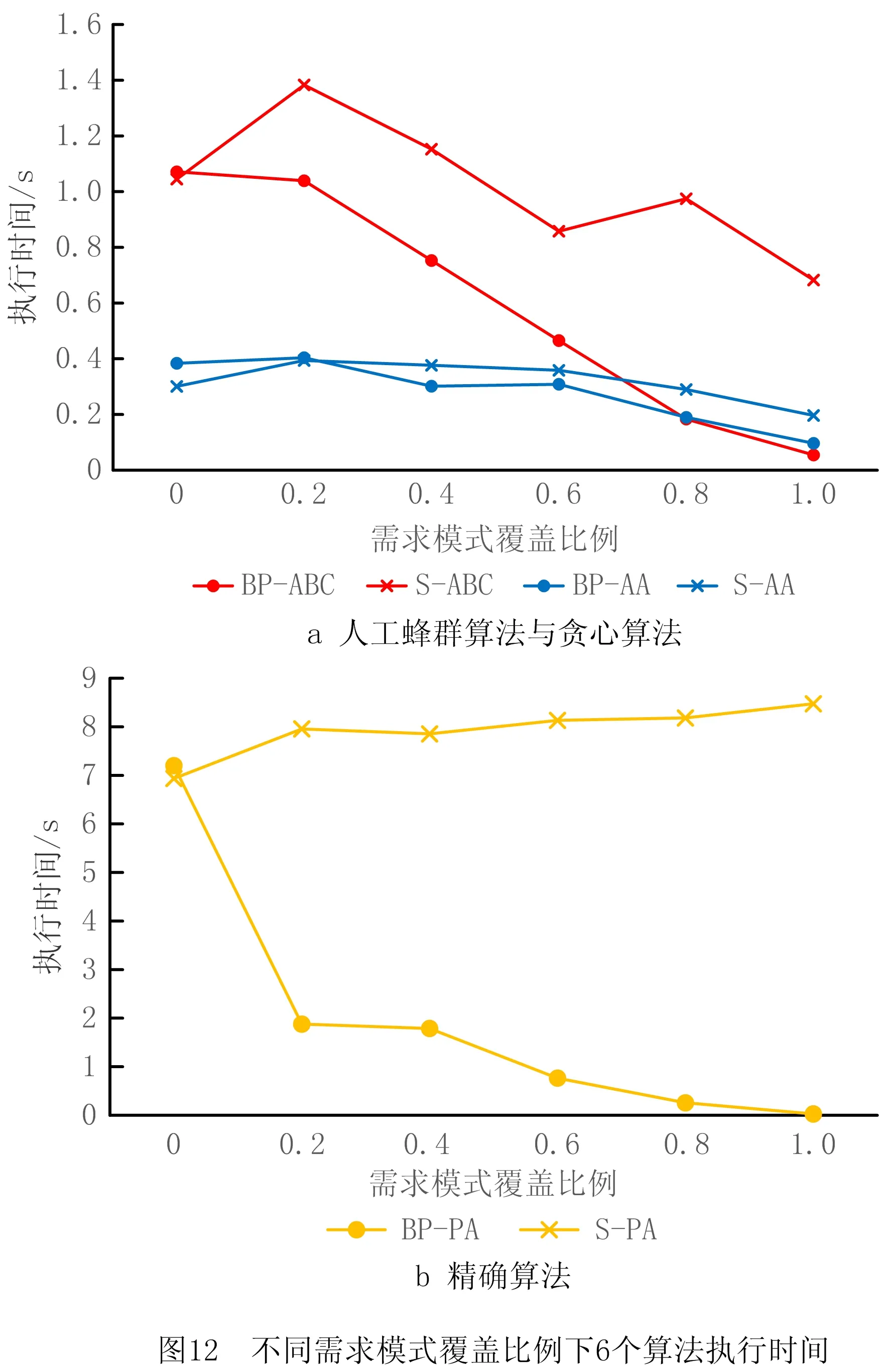

4.3 关联矩阵更新策略实验与分析

5 结束语
