面向多品种小批量制造过程的关键工序识别与聚类分析方法

陈克强，刘伟军，姜兴宇，徐思迪，王 永，刘 傲

(沈阳工业大学 机械工程学院，辽宁 沈阳 110870)

0 引言

由于用户个性化需求日趋多样化和市场竞争愈发激烈，多品种小批量生产模式已成为全球企业的必然选择，但其具有品种规格多且工序复杂、生产批量小且重复生产少等生产特点，导致其制造过程中产品质量难以有效控制。关键工序是制造过程质量控制的关键环节，因此，如何准确有效识别关键工序，并解决关键工序质量特征数据不足问题，是目前多品种小批量制造过程质量控制的关键。因此，研究关键工序的识别与聚类分析是实现多品种小批量制造过程质量控制的前提，也是目前现代质量工程领域研究的热点。

关键工序的识别方法有逐层分解法和影响因素法。逐层分解法是专家根据经验来判定零件的关键特性，零件关键特性所在的工序即为关键工序。MA等[1]针对关键质量特性识别问题，提出基于ReliefF算法的MTS(Mahalanobis-Taguchi System)方法消除无关的质量特性，采用正交表与信噪比确定关键质量特性,从而识别关键工序。TIUC等[2]分析复杂产品的关键特性重要程度、客户需求、生产法规，从而识别复杂产品的关键质量特性，取得了良好的效果。ESTRADA等[3]通过构建系统持续改进模型识别关键特性，解决关键特性存在的问题。张莉等[4]基于装配有向图研究关键特性波动传动，由上层质量特性推导出潜在下层质量特性，利用模糊理论的Dematel方法量化分析下层质量特性集合，确定本层的关键特性。王化强等[5]引入Lasso方法对原始数据进行降维及排序，并利用支持向量机(Support Vector Machine, SVM)分类器进行测试验证，有效地识别多属性高纬度复杂产品的关键质量特性。徐海生等[6]基于图论建立了生产车间的工序模型,并从工序节点与分段产品尺寸精度的相关程度、工序节点对其他节点的影响程度、工序节点质量水平3个方面提出关键工序识别模型,并给出船舶分段车间工序节点关键度的概念和计算公式,衡量模型中工序节点的关键度。

影响因素法即为研究分析关键工序的影响因素，从而识别关键工序。BAGHERY等[7]基于失效模式与影响分析(Failure Mode and Effects Analysis, FMEA)法对产品制造过程进行故障模式及影响分析，计算风险优先数，从而依据风险评价识别关键工序。LATCHOUMY等[8]提出一种可靠性执行模型，通过计算网格中存在的过程故障，确定关键工序。BOGDAN等[9]借助质量功能展开(Quality Functional Deploymen, QFD)与 SIPOC(supplier，input，process，output，customer)方法，针对产品复杂过程的关键工序进行改进。唐任仲等[10]通过构建生产车间模型，利用关键度衡量模型中工序节点的关键程度识别关键工序。王立岩等[11]针对多工序多指标的产品制造过程，改进质量损失函数从而计算质量损失度，进而识别关键工序。陈友玲等[12]从加工过程的角度，构建了工序难度评估体系，运用层次分析法(Analytic Hierarchy Process, AHP)法和群决策理论求解工序难度系数。杨续昌等[13]通过分析影响加工工时的关键因素构建零件制造工序的难度评价指标，基于熵值法与群决策理论考虑各种关键因素，构建零件制造工序的难度系数模型。尹超等[14]通过关键工序的5M1E(man，machine，material，method，measurement，environment)，建立关键装配工序物料质量损失模型及其评价体系，实现对关键装配工序物料质量损失的评估。YUAN等[15]在重新设计因果矩阵方法的基础上，提出了选煤关键过程识别方法，该方法考虑了生产数据集、质量指标，工序与质量特性之间的关系，从而评估关键工序。

针对多品种小批量制造过程中工序样本数量不足的问题,目前国内外研究学者主要分为3个方面展开研究，即数据转换法、过程建模法与贝叶斯预测法。STEINER等[16]提出基于同一工序加工的相似零件的质量数据建立样本集，从而建立质量控制图的设想。WIEDERHOLD等[17]通过识别相似生产过程并将质量特征数据进行聚类分析，增大样本量。周康渠等[18]运用相似性原理分析和判定不同零件工序的相似性，采用相对公差法将工序相似的零件质量数据进行分析转换，建立适合多品种小批量生产的质量控制图，实现统计过程控制(Stotistical Process Control, SPC)对多品种小批量生产过程的质量控制。张根保等[19]利用相似元理论,根据影响工序的各种因素,将与目标工序相似的其他工序合并成组,通过数据转换扩大样本容量,进而利用大样本加工数据对目标工序进行质量控制和工序能力分析。蒋子涵等[20]提出一种新的广义标准灰数概念，结合经典贝叶斯理论，提出一种灰贝叶斯迭代优化控制图模型，并通过次模型在小样本贫信息的情况下监测数据的异常波动。而基于贝叶斯理论的方法虽然在中小批量质量控制中取得了一定效果[21]，但是此类方法的研究多针对单一品种的质量数据，在多品种条件下的控制方法研究明显不足[22]。

逐层分解法识别关键工序属于根据专家经验判定的定性方法，对简单产品的关键工序识别效果明显，但在面对复杂产品时，容易出现误判和错判现象。影响因素法属于对工序关键度的定量评价方法，其分析系统性不足，缺少对工序间影响、加工过程、工序质量的综合考量，容易出现关键工序识别片面性问题。此外，在制造过程中样本数量不足的研究中，多针对单一品种分析其相似工序或先验信息，缺乏对多品种关键工序聚类分析的相关研究。

基于上述分析，多品种小批量制造模式下的关键工序识别应综合考虑关键质量特性与影响关键工序的因素，结合专家经验与影响因素的定量分析，全面、客观、准确地识别关键工序。在此基础上，考虑多品种小批量生产模式下单一品种质量样本的缺乏问题，基于影响关键工序的5M1E六方面因素构建聚类分析指标体系，从而对各品种关键工序进行聚类分析，为后续质量控制提供数据支撑。

1 基于清晰集与灰色关联分析的关键工序识别模型

关键质量特性是对产品的主要功能、安全性、可靠性和成本影响最显著的特性，因此关键质量特性是关键工序的识别过程中最重要的影响因素。基于此，运用清晰集理论中清晰综合评价的方法[23]，对关键质量特性的重要度进行分析；运用灰色关联分析的方法[24]，对关键质量特性与工序的关联度进行评价；最后，基于关键质量特性的重要度和工序与关键质量特性的关联度构建关键工序识别矩阵。

综上所述，关键工序识别模型主要包括关键特性重要度评价、工序与关键质量特性的关联度评价、关键工序关键度计算3个部分。关键工序识别模型构建方法如图1所示。

1.1 关键质量特性重要度分析

关键质量特性(Critical to Quality, CTQ)的重要度，即针对当前产品而言该关键质量特性的重要程度。由于同一产品具有多个关键质量特性，需要对关键质量特性的重要度进行评价。基于清晰综合评价的方法对关键质量特性从实现难度、成本、客户(Voice of Customer, VOC)角度进行评价，得出关键质量特性重要度。该方法综合考虑了专家组评分时的意见情况，评价更为准确、客观。

1.1.1 清晰集理论

定义1清晰集。

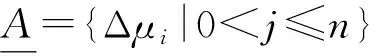
为了研究实际应用，建立清晰数及其四则运算的方法，具体如下：

定义2清晰数。

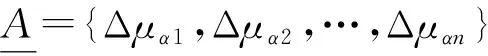
当μα1,μα2,…,μαn相应地用α1,α2,…,αn代替时，得

(1)

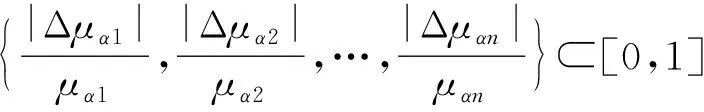
清晰数的均值计算如下：

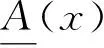
称实数

(2)

1.1.2 重要度分析

基于清晰综合评价的关键质量特性重要度分析方法如下：

(1)建立各因素对应的清晰数

设现有n个有限个专家组成的专家组μα1,μα2,…,μαn，其中αi∈R(1,2,…,n)。各专家组针对某一因素重要度评价时赞成者为Δμα1,Δμα2,…,Δμαn，评分为x1,x2,…,xn，则该因素的清晰数为：

(3)

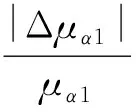
表1 清晰数评分方法

(2)计算综合评判的清晰数

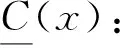
(4)

清晰数的加法运算方法如下：

设清晰数

可能值带边和计算矩阵如下：

隶属度带边积计算矩阵如下：

(5)

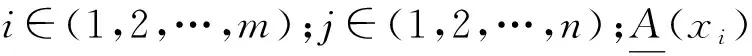
(3)求解清晰数均值

根据清晰数的均值定义，可得：

(6)

关键质量特性的重要度为所求清晰综合评价的结果，即为清晰数的均值。

1.2 关键质量特性与工序的关联度分析

由于每个产品的关键质量特性不唯一，且关键质量特性与工序的关联度也并非一一对应，需要分析各关键质量特性与各工序的关联度。但这种关联度是模糊的、不确定的概念，具有很强的“灰色性”。基于此，采用灰色关联分析的方法，从工序难度、装夹难度、工序质量3方面进行关键质量特性与工序的关联度分析，从而计算出关键质量特性与工序的关联度。

(1)确定关联度评分矩阵

根据式(7)从工序难度、装夹难度、工序质量3个方面计算工序与关键质量特性的关联度：

关联度评分=关联度系数×工序难度×

装夹难度×工序质量。

(7)

其中关联系数CI为关键质量特性所在工序的节点的影响度，即关键质量特性所在工序对其他工序的影响度。通过工艺流程分析并结合可达矩阵分析的方法，可以得到影响度的可达矩阵K=[Pij]n×n，其中n为工序节点的数量，Pij为工序i至工序j的可达性，且有

(8)

因此，含有n个工序的产线模型中工序vi的影响度根据式(9)可计算为：

(9)

由于在实际生产线中，工序的总个数不会大于n，故而可将影响度指标归一化，得到关联系数

(10)

从生产线获取的实际数据，构建关联度评分矩阵。考虑到工序的工序难度与加工公差等级具有直接关系，因此根据公差等级对工序难度进行评分赋值，如表2所示。装夹难度赋值如表3所示。工序质量为该产品在对应工序的废品数。

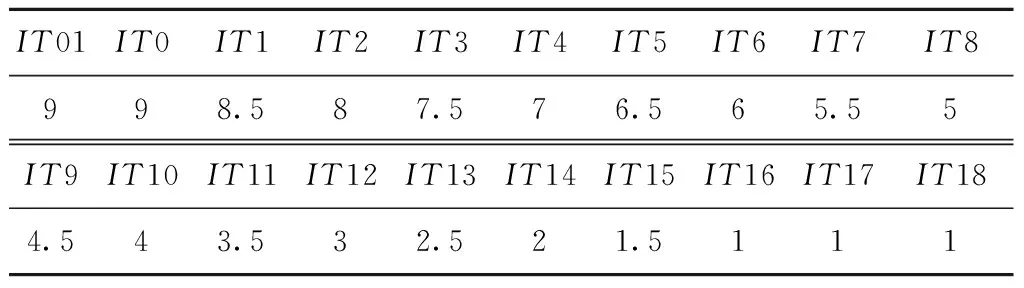
表2 工序难度赋值表

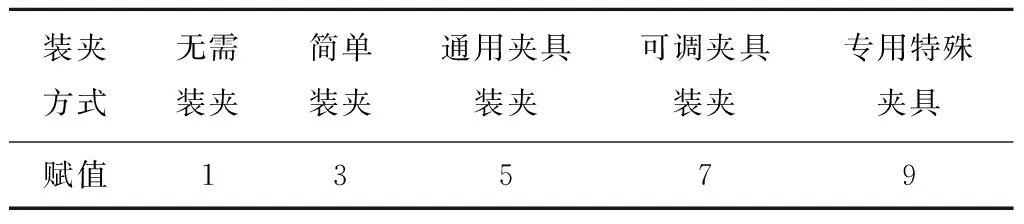
表3 装夹难度赋值表

(2)原始数据的无量纲处理、确定参考序列

为获得正确的分析结果，在确定关联度评分矩阵后，必须对原始数据进行数据规范化变换和处理,使其消除量纲并具有可比性，通常采用初值变换法、均值变换法、百分变换法、归一变换法、倍数变换法等数据变换的方法，本文采用均值变换法，即

(11)

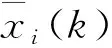
无量纲处理后将无量纲矩阵中各行的最大值选取为最优值，确定参考序列如下：

(12)

(3)计算关键质量特性与工序的关联度

在确定无量纲矩阵和参考序列后，根据式(13)计算评价序列与参考序列的绝对差序列矩阵。根据式(14)计算关键质量特性与工序的关联度Rij，确定关联度矩阵。

(13)

(14)

其中ρ=0.1～1，常取ρ=0.5。

1.3 关键度计算

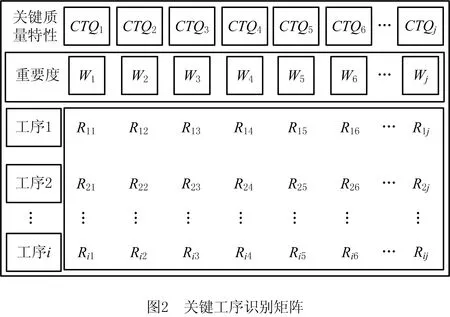
在获得关键质量特性的重要度与关键质量特性与工序关联度矩阵后，构建关键工序识别矩阵，如图2所示，工序的关键系数计算方法如式(15)所示，并根据二八原则确定关键工序。

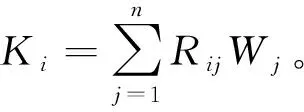
(15)

2 关键工序层次聚类分析

在识别各品种关键工序后，针对影响工序的5M1E(人、机、料、法、环、测)六个方面因素进行聚类分析，构件关键工序聚类分析评分矩阵；在此基础上，根据聚类分析评分矩阵计算聚类距离矩阵，采用层次聚类分析法对关键工序进行聚类分析，为后续质量控制工作提供数据基础。

(1)建立聚类分析指标体系及确定特征值、权重

根据影响工序的5M1E确定聚类分析指标体系，如表4和表5所示。在确定参考关键工序后，获取各二级指标的相似度。二级指标中职业资格等级、企业绩效、设备精度、加工精度、测量系统的重复性和复现性值(Gauge Repeatability and Reproducibility, GRR)为赋值型指标，根据式(16)计算其特征值；其余指标为比较型指标，根据表中赋值方法进行特征值赋值。采用层次分析法确定一级指标与二级指标的权重，其层次结构模型如图3所示。

(16)

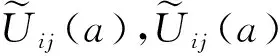
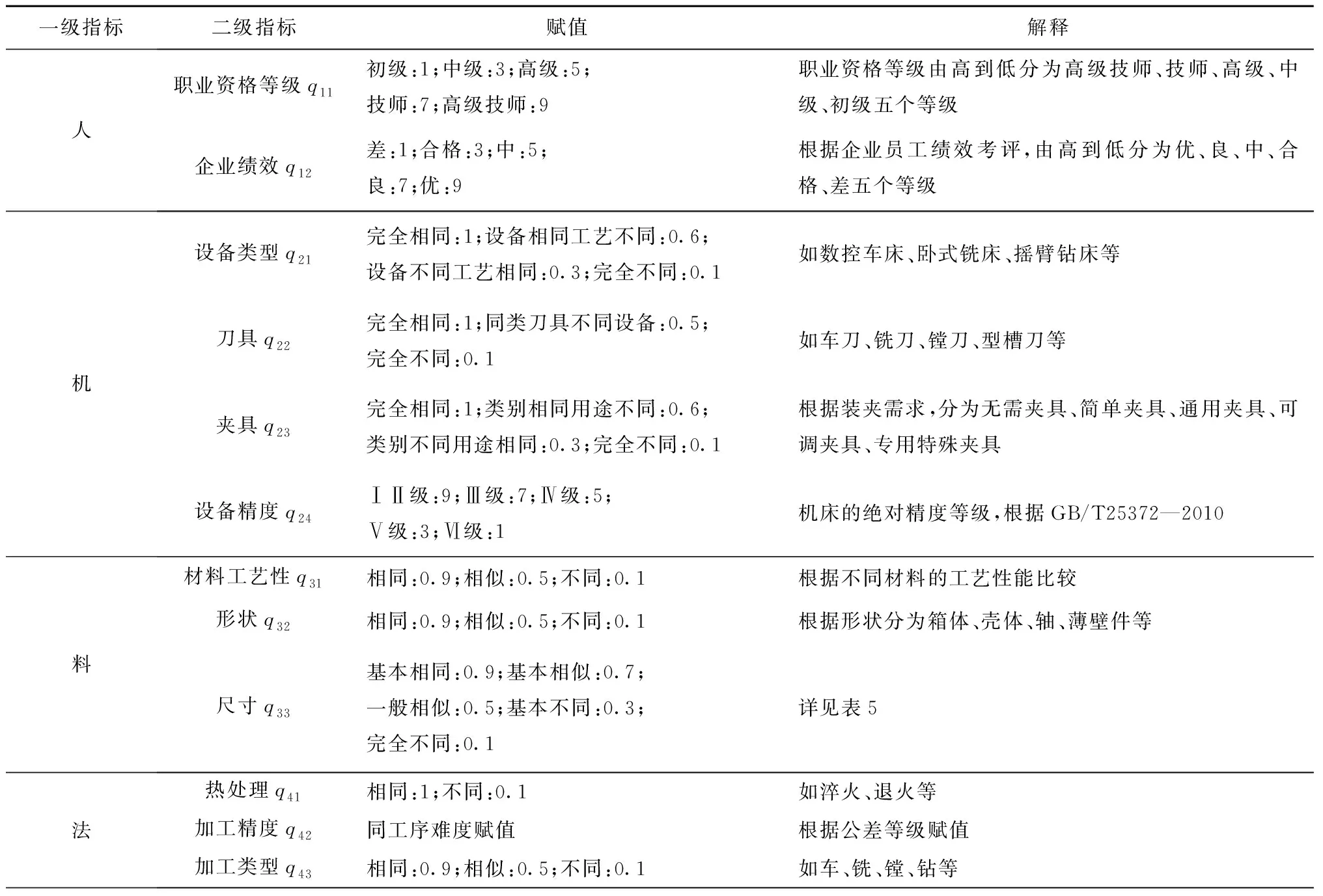
表4 关键工序聚类分析指标体系

续表4

表5 尺寸相似评价表

(2)计算一级指标的特征值与工序特征值

根据各二级指标的特征值与权重，按照式(17)计算各一级指标的特征值。按照式(18)计算工序特征值，并建立关键工序聚类分析评分矩阵。

一级指标特征值

(17)

式中：dij为二级指标权重,rij为二级指标特征值。

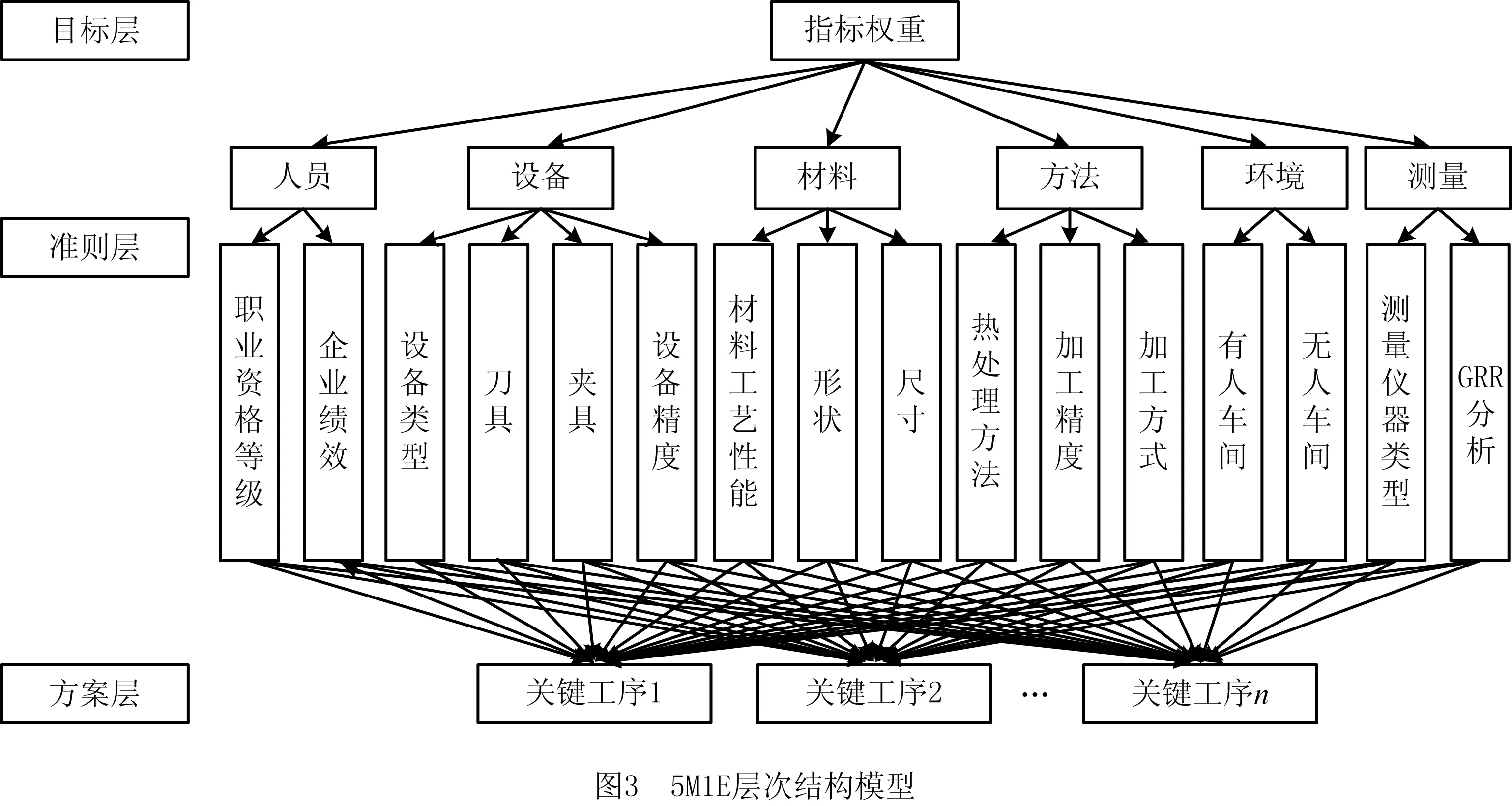
工序特征值

(18)

式中Dij为一级指标权重。

(3)关键工序聚类分析

在获得关键工序聚类分析评分矩阵的基础上，根据式(19)采用欧式距离法计算各关键工序的距离，确定聚类距离矩阵,

(19)

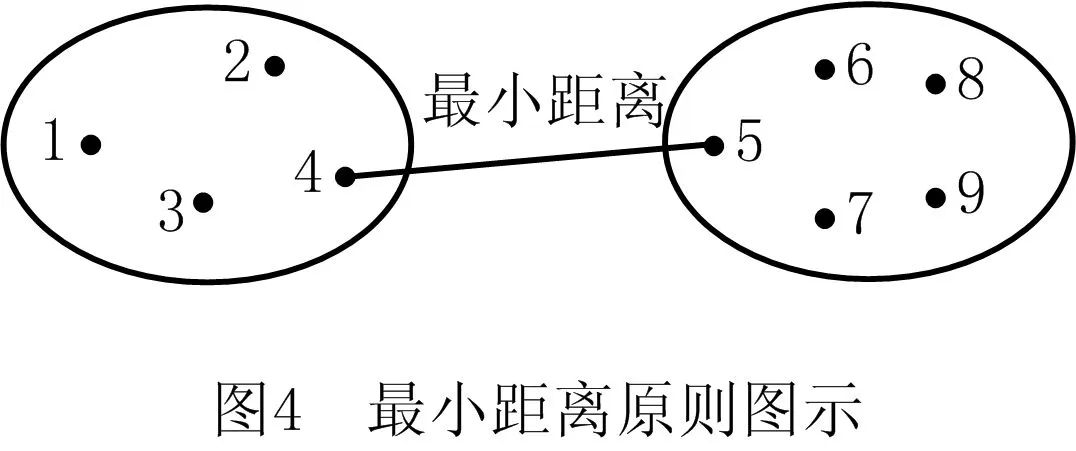
采用凝聚层次聚类分析法,以簇间最小距离的原则计算簇间距离，如图4所示，直到所有对象最终合并至一个簇，输出层次聚类结果。在得出聚类结果后可根据质量控制需求，确定聚类结果的分辨率，根据分辨率截取关键工序的分组方式。

3 实例分析

某航天复杂构件制造企业是典型的多品种小批量制造模式的企业，其产品品种型号多样、产品批量较少、生产过程复杂且不稳定，产品质量无法保证。通过调查分析，发现其产品质量不稳定的主要原因是该企业目前采用的质量管理方式主要依赖于事后检验，没有采用系统的方法识别关键工序，关键工序识别主要依赖于生产经验，对关键工序的质量控制效果不足，无法满足企业的质量需求，导致其质量问题频发。

本文基于上述关键工序识别与聚类分析方法，以其复杂框架类、曲轴类、通道体类、油缸体类4种典型品种为例，采用科学的方法对各品种关键工序进行识别，并对各品种关键工序进行层次聚类分析，从而为该企业的质量控制提供依据与支持，具体如下：

以油缸类零件的加工过程为例，分析其加工过程的关键工序。油缸体每个月生产批量为10～20套，与其他品种零件混线生产。图5为油缸类零件的三维建模与工程图，表6为油缸类零件的加工工艺流程。

由产品技术要求与客户需求可知，油缸体的关键质量特性包括：M36螺纹孔的同轴度；φ32孔的圆度、同轴度与尺寸精度；φ27.5孔的圆度、同轴度与尺寸精度；镜面孔与孔尾端的方槽的共线度；以及孔壁表面粗糙度。基于此，构建关键质量特性集CTQi={M36同轴度，φ32相关特性,φ27.5相关特性，镜面孔与孔尾端的方槽的共线度，孔壁表面粗糙度}。

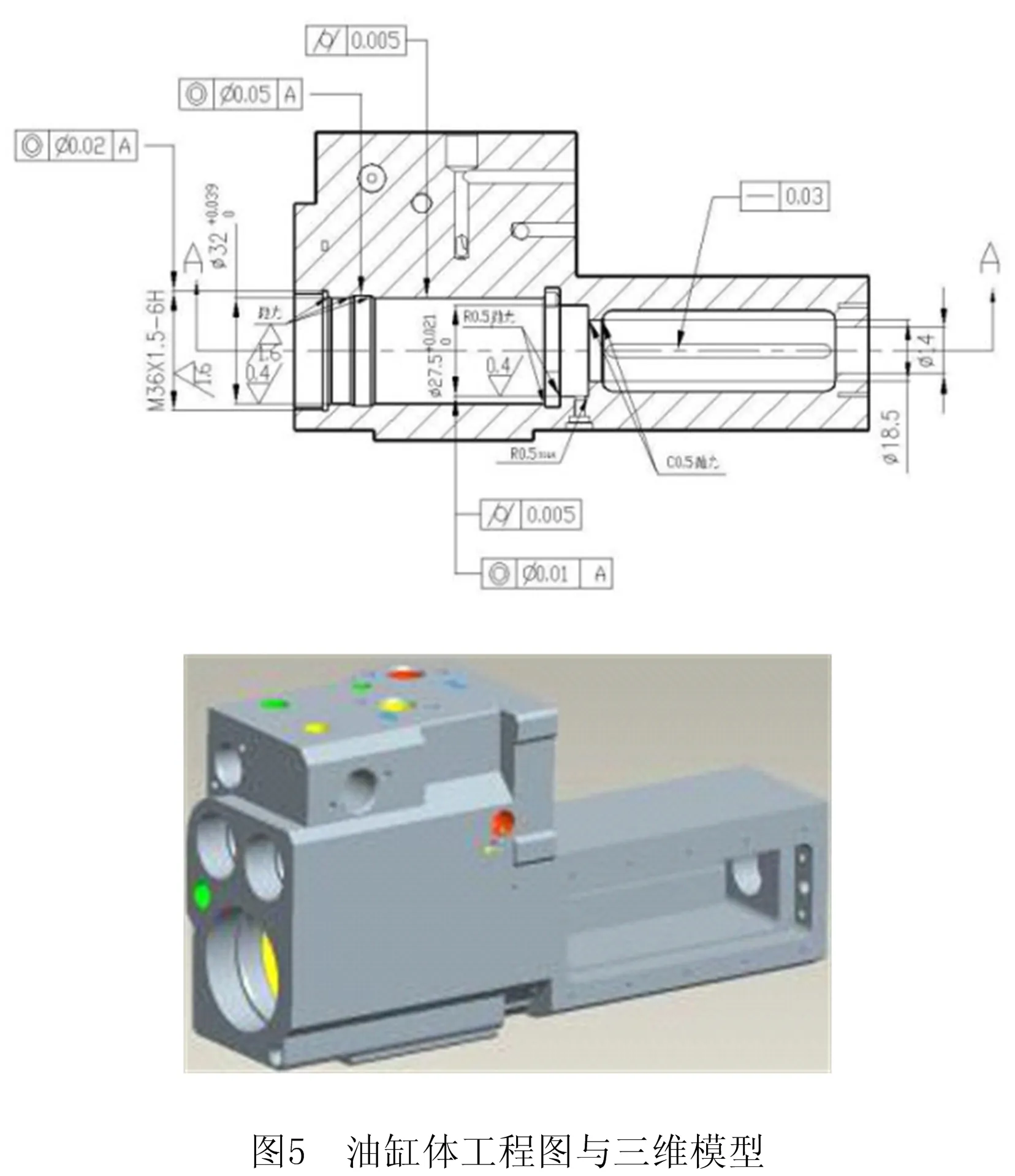
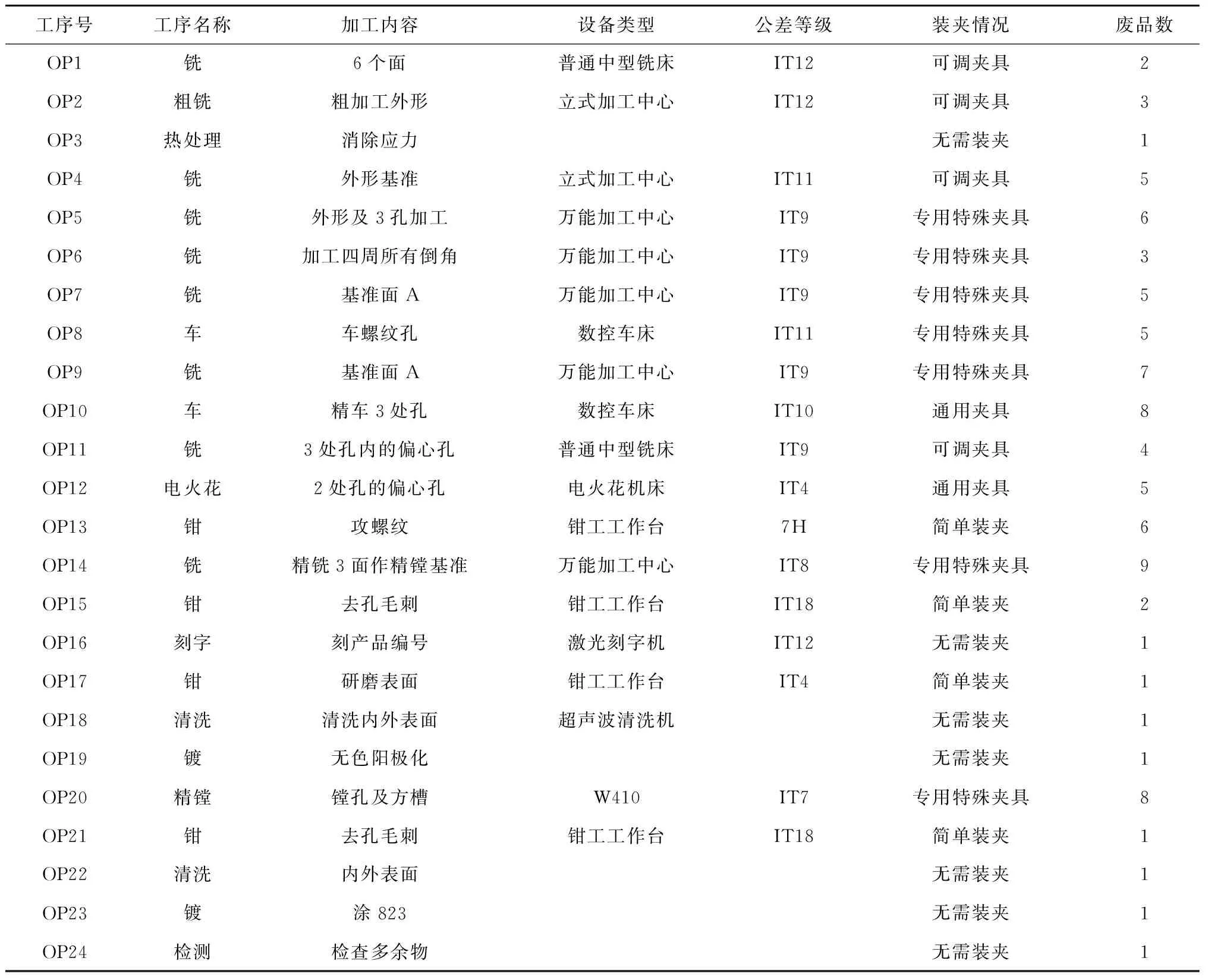
表6 油缸体工艺流程介绍

在此基础上，基于清晰综合评价的方法，从实现难度、成本、VOC三个方面对关键质量特性集中的关键质量特性进行重要度分析，确定各关键质量特性的重要度指标集。采用层次分析法确定实现难度、成本、VOC三个指标的权重，其比较矩阵如下:

实现难度 成本 VOC

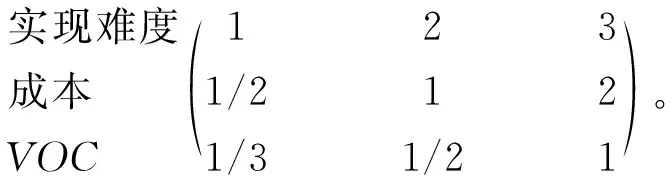
经过计算(过程略)可得：实现难度、成本、VOC三个指标的权重分别为0.548 5,0.302 0,0.149 5。以φ32相关特性为例，各专家组采用清晰综合评价方法从上述3方面对CTQ的清晰综合评价打分，其结果如下：

(1)实现难度

(2)成本

(3)VOC

运用Python语言，在Pycharm软件环境下对以下过程进行计算与求解,根据式(4)针对评价结果(保留4位小数)，对各指标清晰数进行加权计算，结果如下：

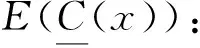
因此可得出该CTQ的综合得分为7.796 2分。基于上述过程，可以得到所有CTQ的评分，如表7所示。

表7 各CTQ的重要度得分

根据油缸体的工艺流程以及CTQ的所在工序，按照式(4)～式(6)计算CTQ所在工序的可达矩阵，即影响度矩阵，如图7所示。

根据式(7)计算CTQ与各工序的关联度，其中缺省值为1,得到关联度评分矩阵；根据式(8)采用均值法对关联度评分矩阵进行无量纲处理，得到无量纲矩阵；根据式(9)～式(11)计算工序与CTQ的关联度，从而确定关键工序识别矩阵；根据式(12)计算关键系数，并根据“二八原则”识别关键工序，程序仿真结果如表8所示。

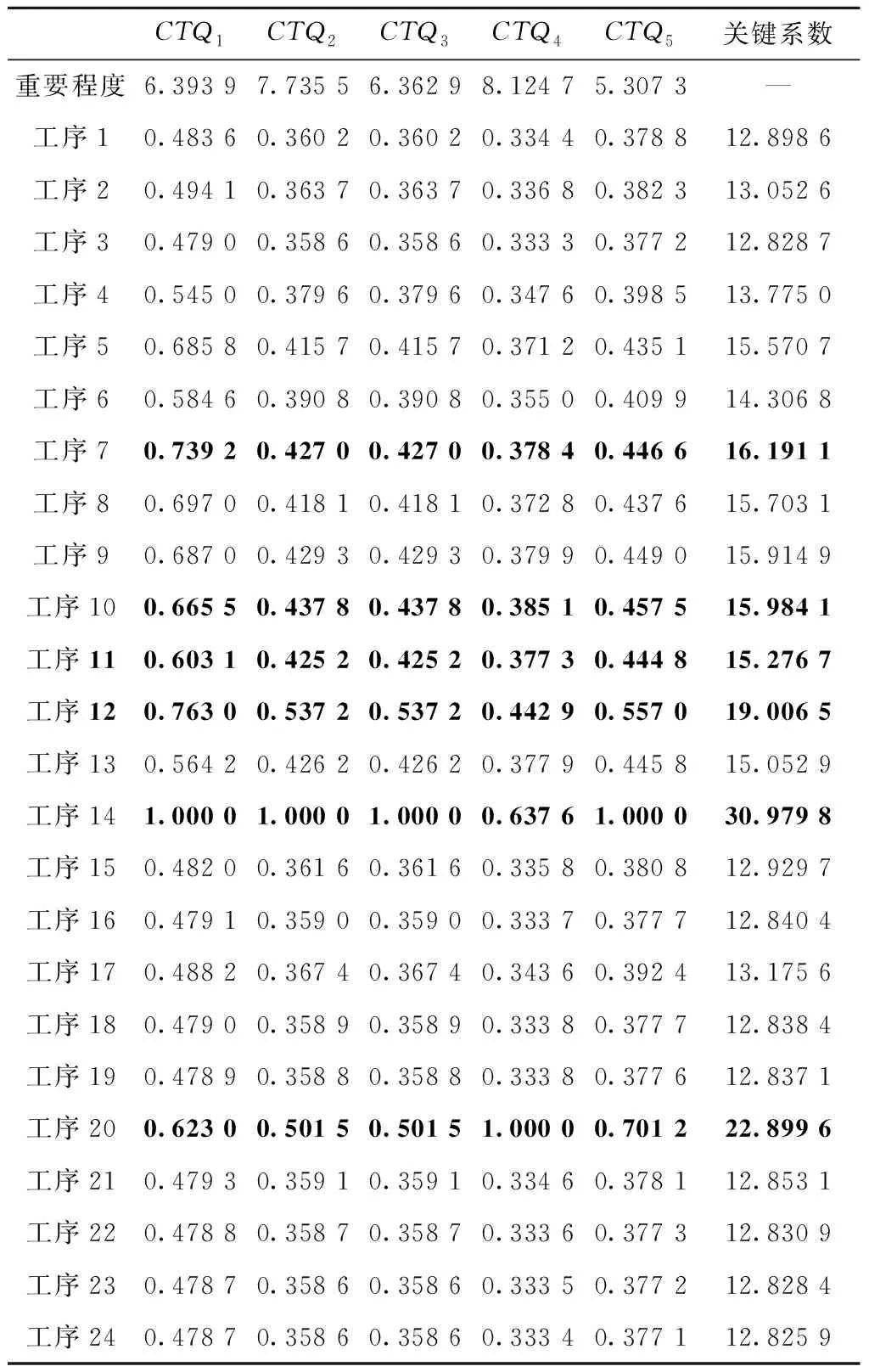
表8 关键工序识别仿真结果

通过分析识别结果，可以得出油缸体加工工艺流程中的关键工序为：工序7、工序10、工序12、工序14、工序20,如表8黑体数据。若用逐层分解法识别关键工序，则应有关键工序的个数为7个。本文方法识别关键工序为5个，相比之下准确度提高了25%左右。与影响因素法相比，本文方法在兼顾了关键质量特性对工序质量的影响的同时考虑了工序间影响、加工难度、装配情况、工序质量对关键工序影响，从而使关键工序的识别更为客观、合理、准确。基于此，上述关键工序的识别方法可识别出该航天复杂构件制造企业内各品种的关键工序，识别结果如表9所示。

表9 各品种关键工序识别结果

在此基础上，根据表4所示的关键工序聚类分析指标体系，获取各关键工序的二级指标相关信息，如表10所示；选定关键工序1作为参考工序，根据表4中的指标赋值方法对各关键工序的二级指标进行赋值，得到特征值矩阵，其结果如表11所示。

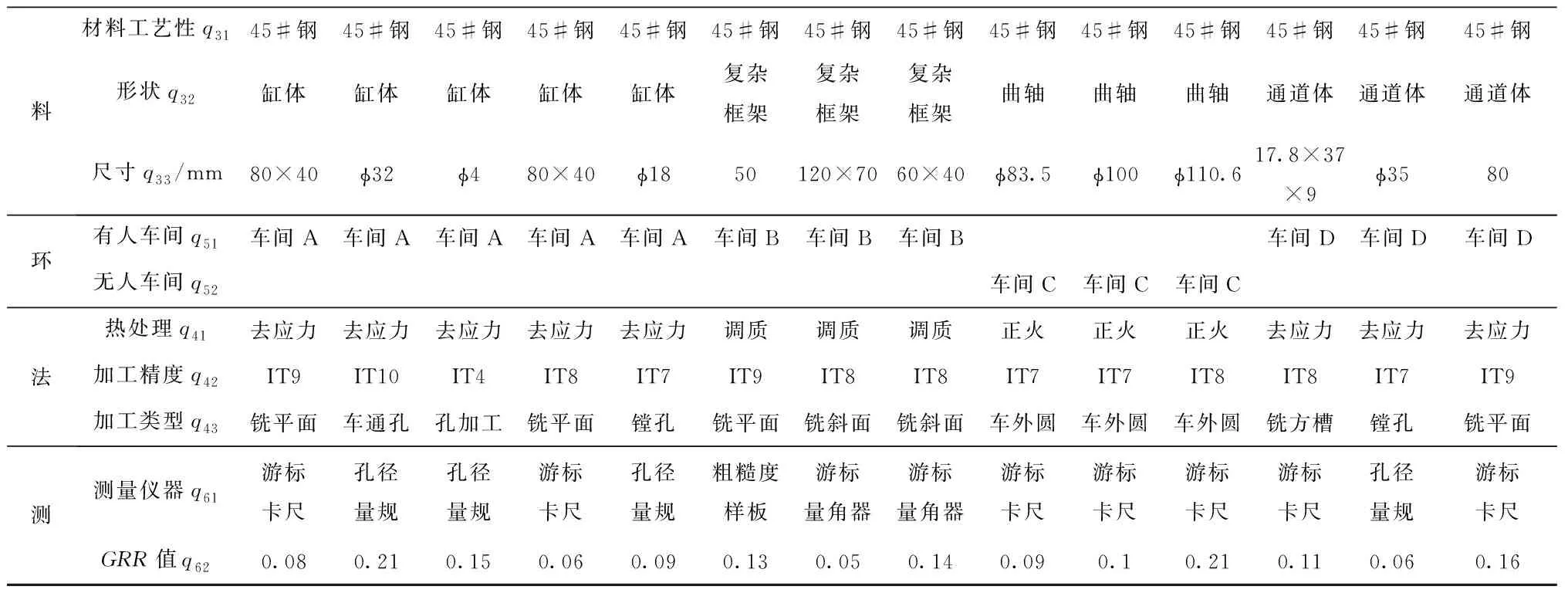
续表10

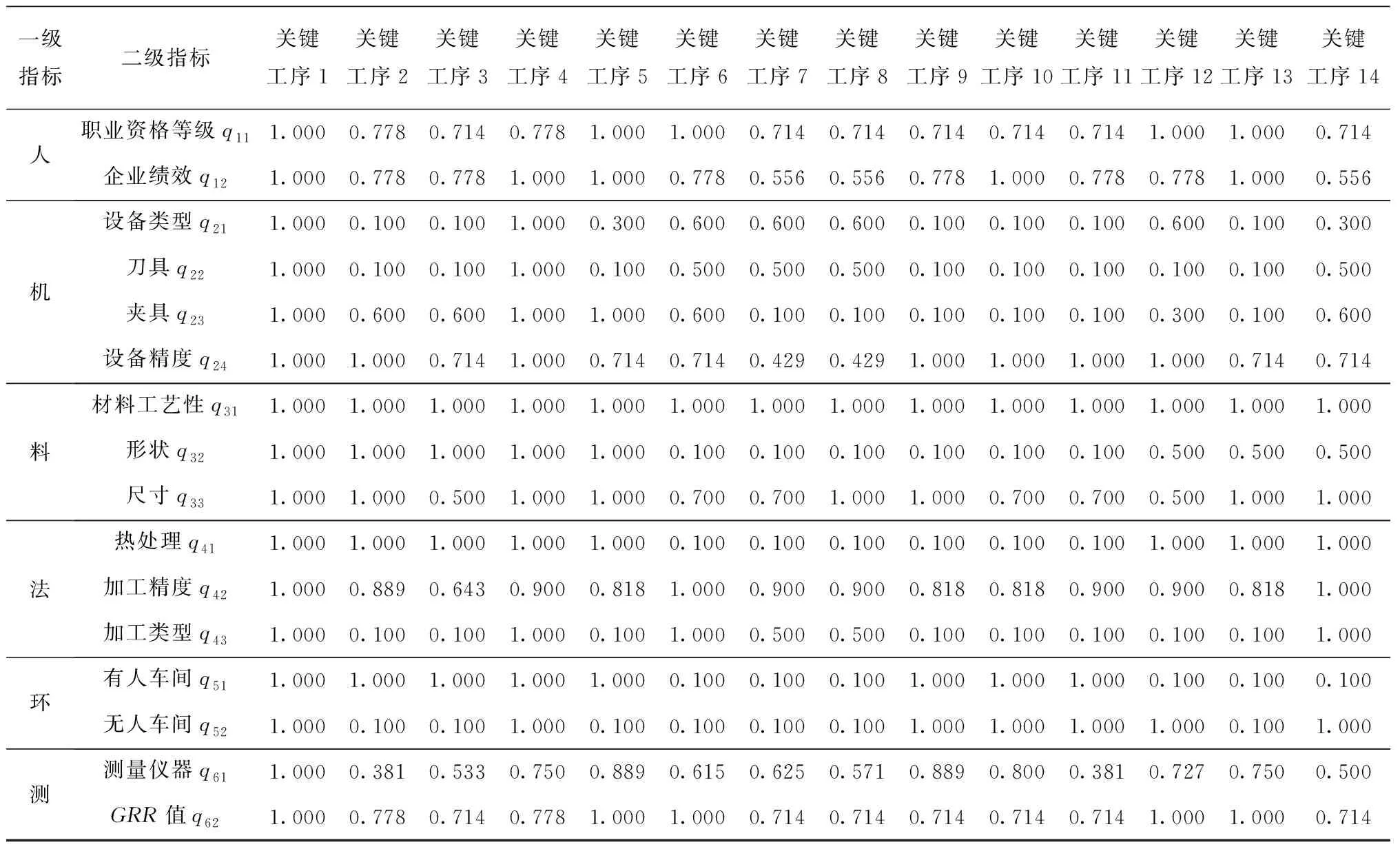
表11 各品种关键工序二级指标特征值

根据表4对比较型指标的特征值赋值。以职业资格等级为例进行，其特征值计算如下：

根据图3中的层次结构模型，对各项指标的权重进行计算，利用AHP法将各一级指标进行两两比较，得到一级指标的判断矩阵，如图6所示。

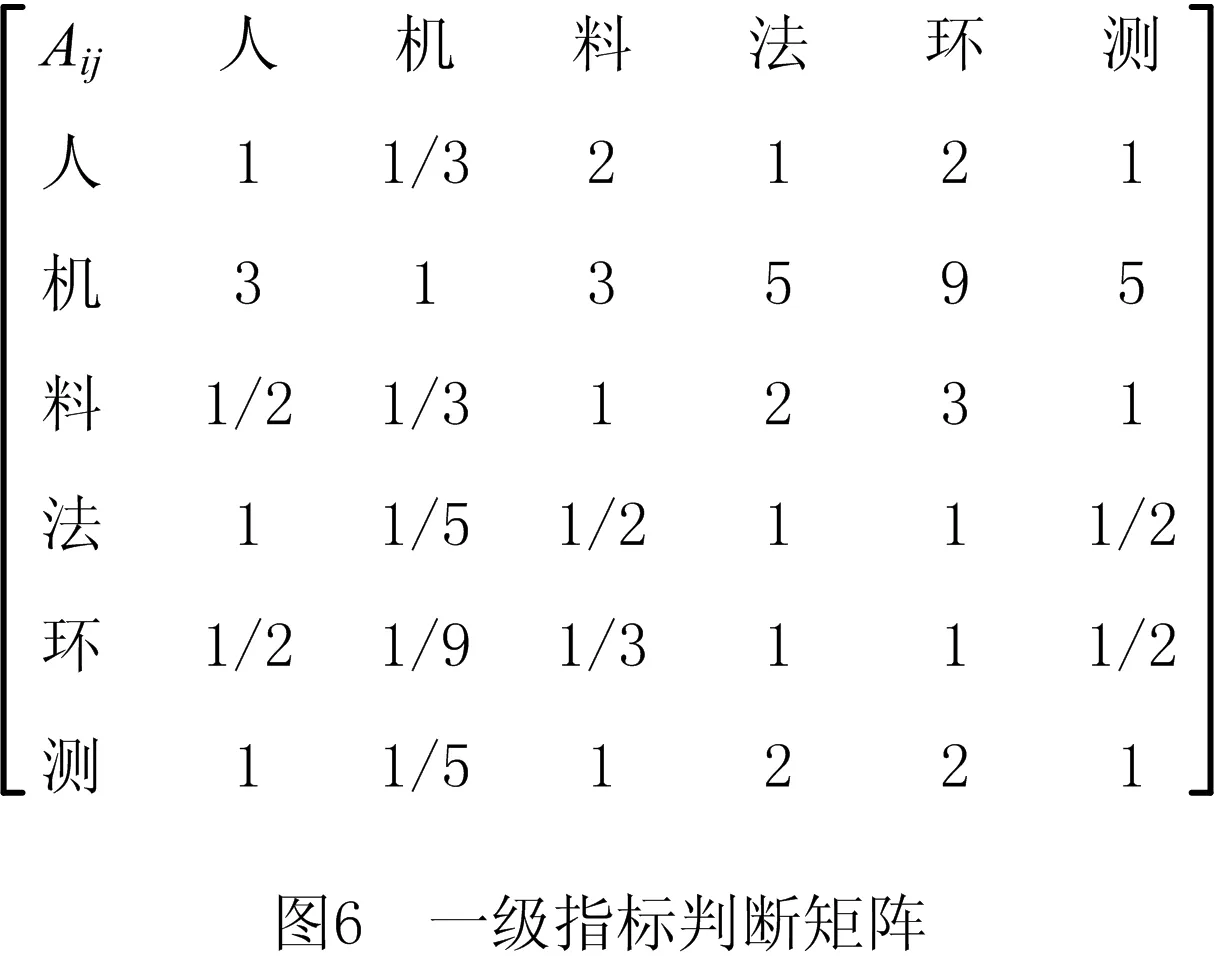
在此基础上，对一级指标判断矩阵进行一致性检验，根据式(17)和式(18)求得判断矩阵对应的特征值。特征结果如下：λmax=6.206，CI=0.041；经查表可得当矩阵阶数为5时，RI=1.26。经计算，CR=0.032<0.1,通过一致性检验。因此，所得特征向量即为一级指标权重，按照5M1E的顺序其权重依次如下：

Di=(0.146,0.415,0.141,0.087,0.072,0.139),

(17)

(18)

采用上述方法对各一级指标下的二级指标分别赋予权重，建立判断矩阵，求出各二级指标权重如表12所示。在此基础上，计算各一级指标特征值，以关键工序3的一级指标“人”为例，其一级指标特征值计算如下：

0.778×0.346≈0.107。

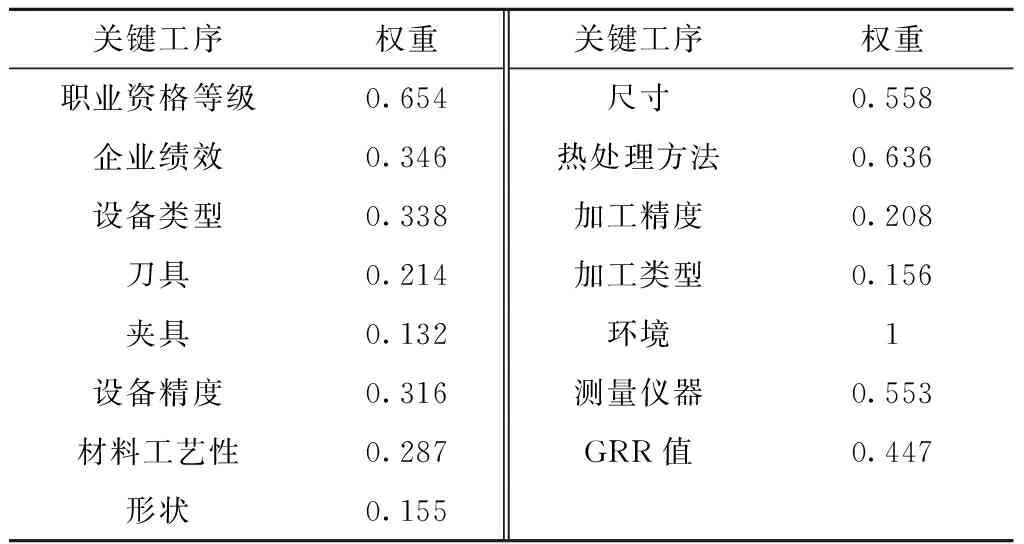
表12 各品种关键工序二级指标权重

根据相似性评分矩阵，采用式(16)欧式距离法计算各关键工序的聚类距离矩阵，并基于最小距离原则计算每次聚类的阈值，直至距离矩阵只有一个值时，凝聚聚类停止。根据凝聚层次聚类的结果绘制出层次聚类树状图，如图7所示。

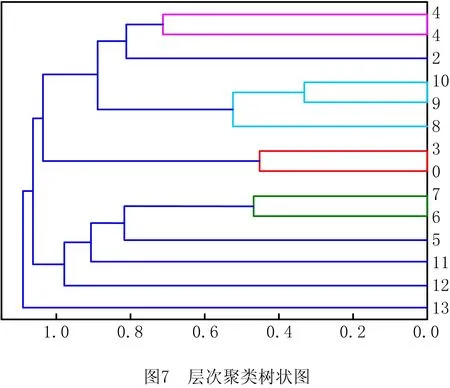
分析层次聚类树状图可知，聚类分辨率可有两种方案：方案一为分辨率为3，与关键工序1相似的关键工序组为{关键工序1、关键工序2、关键工序3、关键工序4、关键工序5、关键工序9、关键工序10、关键工序11}；方案二为分辨率为4，与关键工序1相似的关键工序组为{关键工序1、关键工序4}。若方案二包含的质量数据样本集可以满足样本需求，则选用方案二，且聚类精度最好;若方案二无法满足样本需求，则选用方案一构建质量数据样本集，但聚类精度次之。

4 结束语

本文提出一种面向多品种小批量制造模式的关键工序识别方法，基于清晰集与灰色关联分析的方法，考虑实现难度、成本、VOC三个因素，并根据“二八原则”的思想建立了关键工序识别模型，实现了对产品关键工序的识别。在识别关键工序的基础上，从产品的5M1E角度出发，构建了聚类分析评分矩阵，采用层次聚类分析法对各品种的关键工序进行聚类分析，其聚类结果可为后续质量控制环节提供数据支撑。以某航天复杂构件制企业的实际生产状况为例，运用Python语言对本文的关键工序识别与层次聚类分析方法进行编程仿真，仿真结果验证了本文方法的有效性与可行性。

综上所述，本文考虑了关键工序所涉及的关键质量特性与影响因素，对制造过程的工序关键度进行了定量分析与计算，实现了对关键工序的识别，并对关键工序进行聚类分组。通过程序仿真与实例分析验证了本文方法对准确性、有效性与可行性，可为多品种小批量生产模式下的关键工序研究提供借鉴，为多品种小批量质量控制提供支撑。但由于本文中所涉及的指标权重赋值采用层次分析法，当指标数量过多时，权重确定效率低、一致性差。因此，在指标权重确定方面，还值得继续研究。