基于NSGA-II的冷链物流配送路径多目标优化
2022-04-02常海平李婉莹董福贵郭晓鹏
常海平,李婉莹,董福贵,郭晓鹏
(华北电力大学 经济与管理学院,北京 102206)
随着社会发展和人民生活水平的不断提高,人们对生鲜农产品的需求量不断增加,对生鲜农产品的质量要求也越来越高。据中物联冷链委统计,2019年我国食品冷链物流需求总量约为2.33亿t,同比增长23.52%。根据《2019农产品产地冷链研究报告》数据显示,目前欧美国家已经将生鲜产品的损耗率控制在5%的稳定水平,而我国的生鲜平均损耗率在10%以上,是欧美国家的2~3倍,并且我国果蔬、肉类、水产品的冷藏运输率分别为35%、57%、69%,而发达国家平均冷藏运输率高达90%以上。虽然近几年我国冷链物流实现了快速发展,但与发达国家比较仍有较大差距[1]。物流业的高速发展,物流各环节对能源的需求越来越多,由此产生的CO2也越来越多。2020年9月,习近平总书记提出我国CO2排放力争于2030年前达到峰值,努力争取2060年前实现碳中和;碳达峰、碳中和目标彰显了我国主动承担应对气候变化的国际责任、推动构建人类命运共同体的坚定决心[2]。因此,要加大对物流业的监管力度,控制化石能源总量,不断实行可再生能源替代行动。
电子商务的迅速发展以及其方便、快捷的消费形式,使人们对生鲜农产品的需求也越来越多样化,冷链物流已成为国内外学者的关注热点。许婷婷等[3]考虑了车辆运输成本、货损成本、时间成本、温度成本,构建以成本最小为目标的优化模型。邓红星等[4]构建了基于随机需求且带有软时间窗的最小配送成本函数模型,利用改进的遗传算法求解。朱泽国等[5]考虑了在路段通行时间不确定背景下,多种车型车辆配送的组合优化。Qi等[6]基于应急冷链物流资源的最短调度时间,构建了应急冷链物流调度的数学模型。Amorim等[7]针对易腐食品的配送问题,建立了成本最小化和产品新鲜度最大化的多目标模型。在此基础上,碳排放量也受到了越来越多专家和学者的关注,温喜梅等[8]考虑了碳排放环境下对多配送中心车辆路径规划问题的影响研究。Zhang等[9]将低碳经济引入冷链物流,建立了包括碳排放成本在内的冷链物流路线优化模型。冷链物流配送路径模型从最初的单目标到双目标,再逐渐演变成多目标,侯宇超等[10]提出三个目标:客户满意度、总成本、大气污染物和温室气体排放量,将客户满意度作为主要目标,并利用精英蚁群算法进行求解。Bortolini等[11]提出了同时考虑运营成本、碳足迹和配送时间的多目标生鲜农产品配送网络优化模型。Song等[12]分析了包含每个客户的调度时间窗口、不同类型的车辆以及每辆车的不同能耗和容量的冷链物流系统中的车辆路径优化问题,利用改进的人工鱼群(IAFS)算法进行求解。Zulvia等[13]研究了易腐产品的绿色车辆路线问题,考虑了时间窗口、高峰时段和非高峰时段的不同出行时间以及工作时间,并使用多目标梯度演进(MOGE)算法求解模型。
很多专家学者已经从不同成本、目标及算法对冷链物流配送进行了研究,并取得了一定成果。但冷链物流配送路径优化模型仍存在以下问题:
1)虽然研究的配送优化模型从单一的成本目标到多目标演变,但在求解过程中,多数学者选择主要目标法,未将各目标的重要程度进行合理量化。因此,文中在考虑多目标的基础上,提出模型求解算法,即先通过NSGA-II[14-15]求得Pareto最优解,再结合层次分析法(AHP)求得各目标权重,对各目标的重要程度进行了赋权量化,最后选出最优满意解。
2)多数作者将生鲜农产品的新鲜度或准时送达率作为客户满意度的量化参考,而文中将生鲜农产品的新鲜度和准时送达率均作为客户满意度的量化参考,考虑更加充分,更接近实际问题需要。
1 冷链物流配送路径多目标优化模型建立
1.1 模型假设及约束
将车辆配送路径优化模型抽象为数学模型,为方便模型构建,需做以下假设:
1)为一配送中心、多客户需求的配送路径优化研究,订单确定后,客户的地理位置不再改变,且生鲜农产品的需求量为已知;
2)配送中心能够满足所有客户需求,配送当天所有产品均完成装车;
3)配送车辆为带有冷冻或冷藏设备的货车,在配送过程中始终保持匀速行驶,忽略交通拥堵延误配送情况;
4)生鲜农产品在运输途中车内保持低温不变状态,运输过程中和开启车门卸货时都会产生货损成本,同时,生鲜农产品新鲜度下降;
5)车辆出发后,不能对车辆进行路线更改,车辆的始末点均为配送中心。
1.2 模型目标函数构建
1.2.1 客户满意度目标
客户满意度评价指标包括生鲜农产品新鲜度和准时到达率。
1)生鲜农产品新鲜度。生鲜农产品在配送过程中,其新鲜度会不断下降,造成新鲜度下降的主要原因为时间累积和环境温度较高。文中将生鲜农产品的新鲜度分为三个阶段:第一阶段,在T0时间内,生鲜农产品的变质率为0,保持100%的新鲜度;第二阶段,货物在运输过程中时间累积变质率为∂1,打开车门后的变质率增加为∂2(∂2>∂1),新鲜度呈指数下降;第三阶段,产品品质下降到一定程度,无法进行销售,不被市场接受。文中主要考虑第二阶段的农产品新鲜度下降情况。
当车辆从配送中心出发到达客户时,不考虑开启车门所引起的新鲜度下降,只考虑车辆运输过程中时间累积造成的农产品新鲜度下降,生鲜农产品的新鲜度损失为
(1)
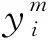
当开启车门时,外界热空气会进入车厢,车内温度会有所上升,此时由于温度上升导致的农产品新鲜度下降[16],变质率为∂2,车辆在卸货时开启车门造成的生鲜农产品新鲜度损失为
(2)
式中:θ2∈[0,1];Qim为车辆m离开客户i时车上的生鲜农产品重量;tis为客户卸货所需时间,设装卸效率为ui,则卸货时间可表示为qi/ui。
2)准时到达率。车辆在配送过程中,会考虑路程、需求量等各种因素,优先选择一些客户进行配送,因此,对于客户提出的期望时间窗并不能保证全部满足,部分客户无法准时配送。
文中提出双边下降的混合时间窗客户满意度模型,将准时到达率作为客户满意度的一部分。设客户的期望时间窗为[ti a,ti b],车辆提前或延后到达都会使客户满意度呈线性下降,当车辆在ti o之前或在ti c之后到达,准时到达率均为0%,客户拒绝接受服务[17]。利用混合时间窗及车辆实际到达时间求出车辆的准时到达率θi t,客户i的准时到达率函数为
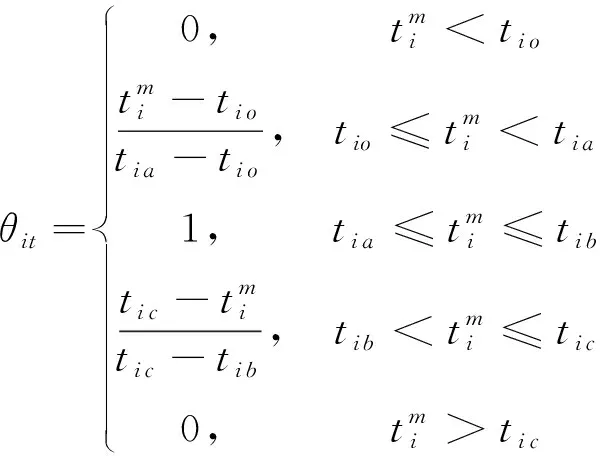
(3)
式中:ti a,ti b分别为准时到达率为100%的时间早晚临界点;ti o,ti c分别为准时到达率为0%的时间早晚临界点。
根据客户的准时到达率函数,可画出如图1所示的准时到达率曲线。
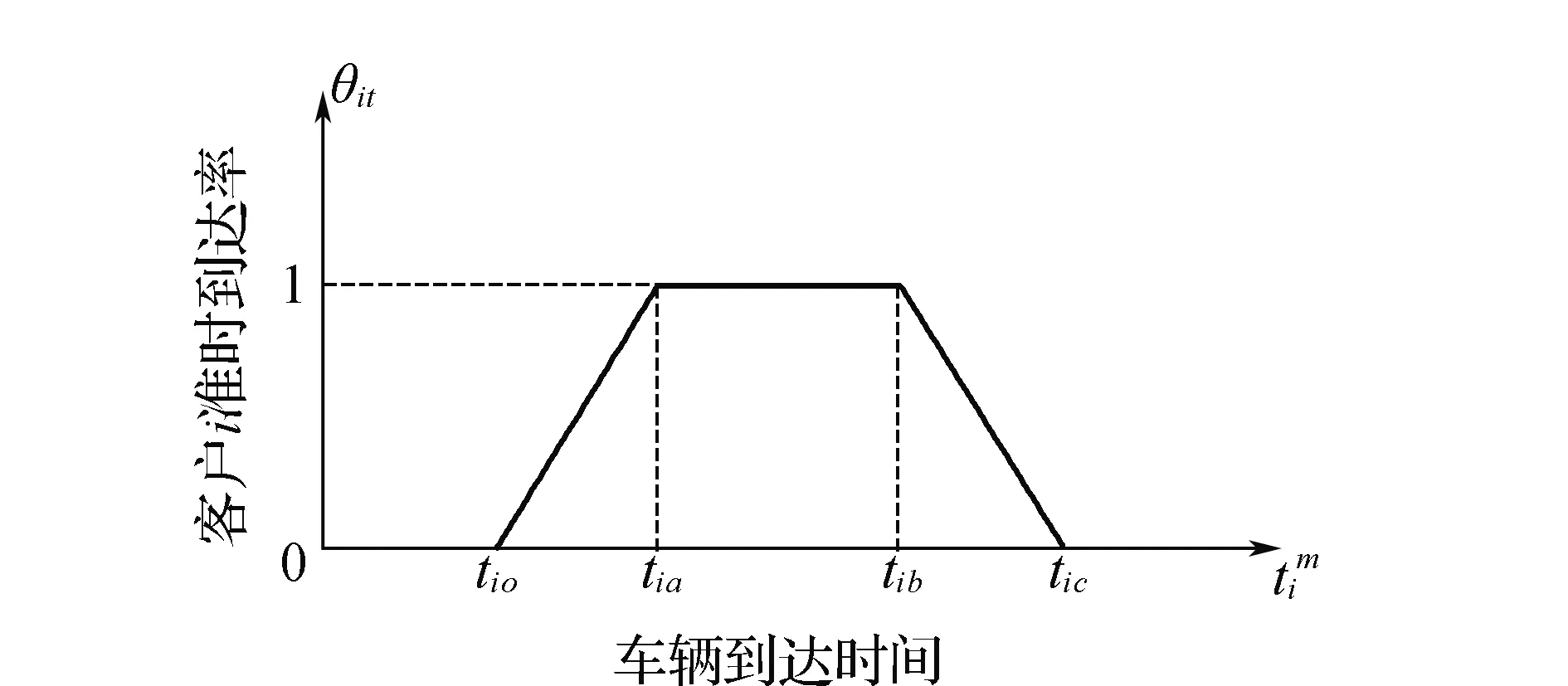
图1 客户i的准时到达率
当客户准时到达率为θi t时,所有客户的综合准时到达率θt可表示为
(4)
1.2.2 物流成本目标
将冷链物流配送的总成本分成4个组成部分,即固定成本、运输成本、制冷成本和时间窗惩罚成本。
1)固定成本。车辆在配送生鲜农产品的过程中,产生的固定成本主要有车辆损耗折旧以及驾驶员工资等成本,其大小不随客户及行驶里程的多少改变,固定成本C1可表示为
(5)
式中:fm为车辆m的配送固定成本。
2)运输成本。运输成本包括车辆的油耗、维修和保养成本等,其大小随客户及行驶里程的多少改变,运输成本C2可表示为
(6)

3)制冷成本。制冷成本包括运输过程中为维持车内温度而产生的制冷成本以及卸货打开车门后为抵消外界热空气所产生的制冷成本。其中,运输过程中产生的制冷成本与车内外温度差和行驶时间有关;卸货时产生的制冷成本主要是车门打开时发生热交换[18],该成本与车门打开程度、打开时间和车内外温差有关。
运输过程中产生的制冷成本C3d可表示为
(7)
Gt=(1+α)RSΔT
(8)
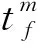
当打开车门卸货时,为保证温度,需要增加制冷,由此产生的制冷成本C3u表示为
(9)
Gs=(0.54V+3.22)·ΔT·β
(10)
式中:Gs为车辆打开车门后的热负荷,ti s为卸货时间,V为车厢体积;β为开门的程度系数。
4)文中研究带混合时间窗的车辆配送路径优化问题,当客户的可接受时间窗为[ti o,ti c],配送车辆在该时间窗内到达无惩罚成本;当车辆提前到达时需要在原地等待,当延后到达有相应惩罚成本,惩罚系数分别为σ1,σ2,其中,σ1为车辆提前到达单位时间的惩罚成本,σ2为车辆延误发生的单位时间惩罚成本。根据上文提出的准时到达率函数,客户i的时间窗惩罚成本C4i可表示为

(11)
客户的时间窗惩罚成本函数如图2所示。
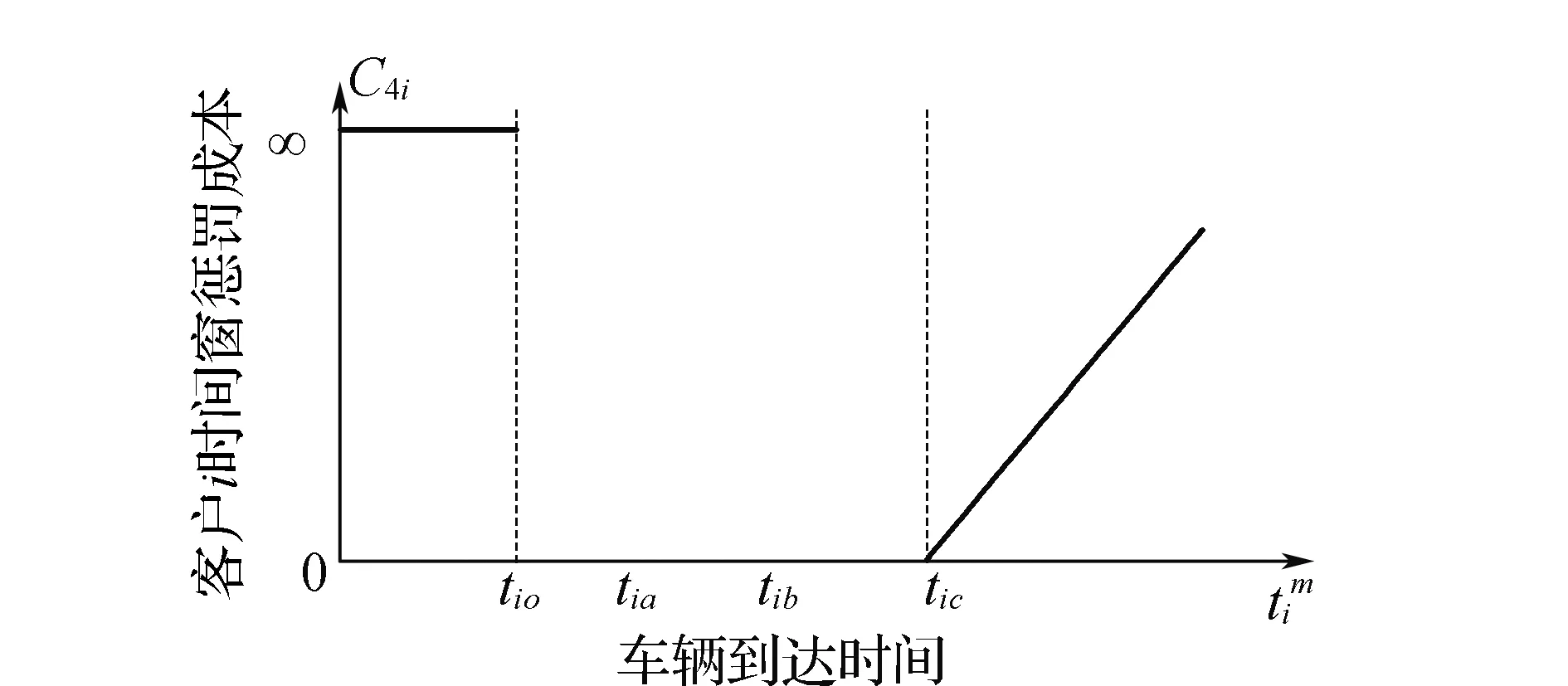
图2 客户i的时间窗惩罚成本
1.2.3 碳排放目标
文中研究的碳排放量指的是CO2排放量E。车辆在配送过程中的碳排放主要包括两方面:车辆行驶过程中燃料消耗排放的CO2E1,以及制冷设备制冷产生的CO2E2。对于车辆配送过程中燃料消耗产生的CO2排放量,文中假设为线性相关,计算碳排量的公式为:碳排放量=燃料消耗×CO2排放系数。燃料消耗不仅与运输距离有关,而且受车辆载重能力和其它因素影响。当车辆空载重量为Q0,载货量为X′(自变量),单位距离燃料消耗量为Y′(因变量),可得到下式
Y′=a(Q0+X′)+b
(12)
若车辆的最大载货量为Qmax,且满载时车辆行驶单位距离的燃料消耗量为Y*,空载时车辆行驶单位距离的燃料消耗量为Y0,则上式可得
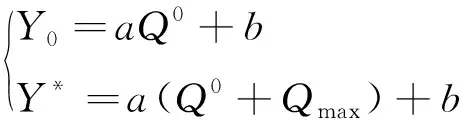
(13)
(14)

(15)
式中:e0为CO2排放系数,Qi m为车辆m离开客户i时车上的生鲜农产品重量。
制冷设备制冷时产生的CO2量,与车中剩余生鲜农产品的质量和车辆行驶距离有关[19],设备制冷的碳排放量E2可表示为
(16)
式中:ω为制冷的单位碳排放量。
1.3 建立冷链物流配送路径多目标优化模型
综上所述,冷链物流多目标配送路径优化模型可表示为以下几个方面。
1)决策变量
2)目标函数
3)约束条件
(20)
(21)
(22)
(23)
(24)
其中,式(17)表示客户满意度最大化目标;式(18)表示物流成本最小化目标;式(19)表示碳排放量最小化目标;式(20)表示每位客户只能由一辆车服务;式(21)表示提供配送服务的车辆从配送中心出发,配送任务结束后返回配送中心;式(22)表示总的服务客户数量为n;式(23)表示每辆车服务客户的总需求不能超过最大载重量;式(24)表示配送到客户j的时间。
2 模型求解设计
在冷链物流配送过程中,存在“效益背反”特性,即多个目标之间相互冲突,无法均达到最优水平。此外,路径优化的搜索空间极为复杂,一些传统的规划方法已无法求出最优解,文中采用NSGA-II进行求解,搜寻Pareto解集,在此基础上结合AHP进行综合评判求解。
2.1 NSGA-II求解过程
1994年,由Srinivas N和Deb K提出了非支配排序遗传算法(NSGA),算法根据个体之间的支配与非支配关系分层实现。Deb K等人进一步改进NSGA,提出了NSGA-II,相比之下NSGAII的计算复杂度降低,耗时较短,提出的拥挤度比较算子很好地保持了种群多样性,增加的精英策略可以在一定程度上确保已经找到的满意解不被丢失,迅速提高种群水平。
步骤1 编码和解码
根据冷链物流车辆配送路径的特点,文中采用自然数全排列编码方式,用0表示配送中心,用1,2,…,n表示需求客户点。配送中心拥有M辆货车,多辆货车同时配送。为了在编码的一条染色体上包含所有的配送路径信息,文中采用增加M-1个虚拟配送中心的方法,分别用n+1,n+2,…,n+M-1表示[20],所以染色体由1,2,…,n+M-1个互不重复的自然数组成,通过染色体解码可得到配送路径方案。如,冷链配送中心用3辆车进行配送,现有8个需求客户,染色体由1,2,…,10(9,10表示配送中心)个自然数随机全排列组成。
1)染色体编码58749106312表示的配送路径为:路径1为0-5-8-7-4-9(0);路径2为10(0)-6-3-1-2-0,共有2条配送路径。
2)染色体编码36295810174表示的配送路径为:路径1为0-3-6-2-9(0);路径2为9(0)-5-8-10(0);路径3为10(0)-1-7-4-0,共有3条配送路径。
步骤2 初始群体
根据编码的生成方法, 染色体由1,2,…,n+M-1个随机全排列组成。结合实际情况,并不是所有随机生成的染色体都可以构成有效染色体。例如约束条件式(23),每辆车服务客户的总需求不能超过该车的最大载重量,因此,要判断染色体是否为有效染色体,需要对每条路线均进行超载判断,任意一条路径超载,该染色体便视为无效染色体。具体判断方法为:将随机生成的全排列染色体解码成具体的配送路径,然后对每段路径进行超载验证。染色体编码36295810174对应3条配送路径,分别为:路径1为0-3-6-2-9(0),路径2为9(0)-5-8-10(0),路径3为10(0)-1-7-4-0。对于路径1,将客户3、6、2、9的需求量累加,若结果大于车辆最大载重量,则认为超载,该条染色体为无效染色体,否则继续验证路径2,依此类推,只有所有的路径都不超载,才可以判定为有效染色体。有效染色体数目逐渐增加,直到达到规定数量为止,最终构成初始群体。
步骤3 快速非支配排序
假设种群为P,规定每个个体k含有2个参数nk和Sk,nk表示P中支配个体的解个体数量,即比个体k优的个体数,Sk表示P中被个体k支配的解个体集合,即比个体k劣的个体集合。个体的优劣可以通过比较各目标函数值的大小进行判断,当配送路径优化模型为多目标函数时,对每个目标函数值进行逐一优劣比较。实现快速分层步骤为
1)找出种群中所有nk=0的个体,并保存在当前集合F1中;
2)对当前集合F1中的个体,从第一个个体开始,遍历其支配解集合Sk中的每个个体l,执行nl=ni-1,如果nl=0,则将l保存在集合H中,重复以上操作,直到F1中的个体全部完成筛选;
3)F1中得到个体组成第一个非支配层,并赋予该非支配层内每个个体相同的非支配排序等级krank(krank=1,2,3…);
4)以H为当前集合,重复步骤2)和步骤3)的操作,直到整个种群被分层[21]。
步骤4 确定拥挤度
拥挤度是指在指定种群中某一个体周围的个体密度大小,用kd表示,个体k的拥挤度等于它在同一层级相邻的点k-1和k+1组成的矩形平均边长,如图3所示。

图3 个体k的拥挤度
为实现拥挤度计算,首先,将有效染色体解码,并进行快速支配排序,将整个种群分成不同的非支配层,然后计算每一层级的拥挤度,具体计算步骤为
1)对同一层级的个体初始化距离,令L[k]d=0(L为种群中的非支配集)。
2)对同一层级的个体,在目标函数Z下对个体进行非支配排序,可表示为
L=sort(L,Z)
(25)
式中:sort( )表示对个体进行非支配排序。
3)规定同一层级的最大及最小个体的拥挤度为无穷大,即L[0]d=L[l]d=∞。
4)对同一非支配集其他个体进行拥挤度计算,算式为
(26)

5)对不同的目标函数重复步骤2)—4)操作。
步骤5 选择操作
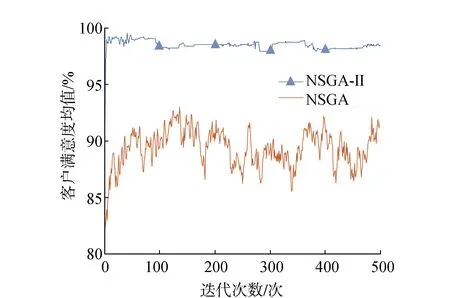
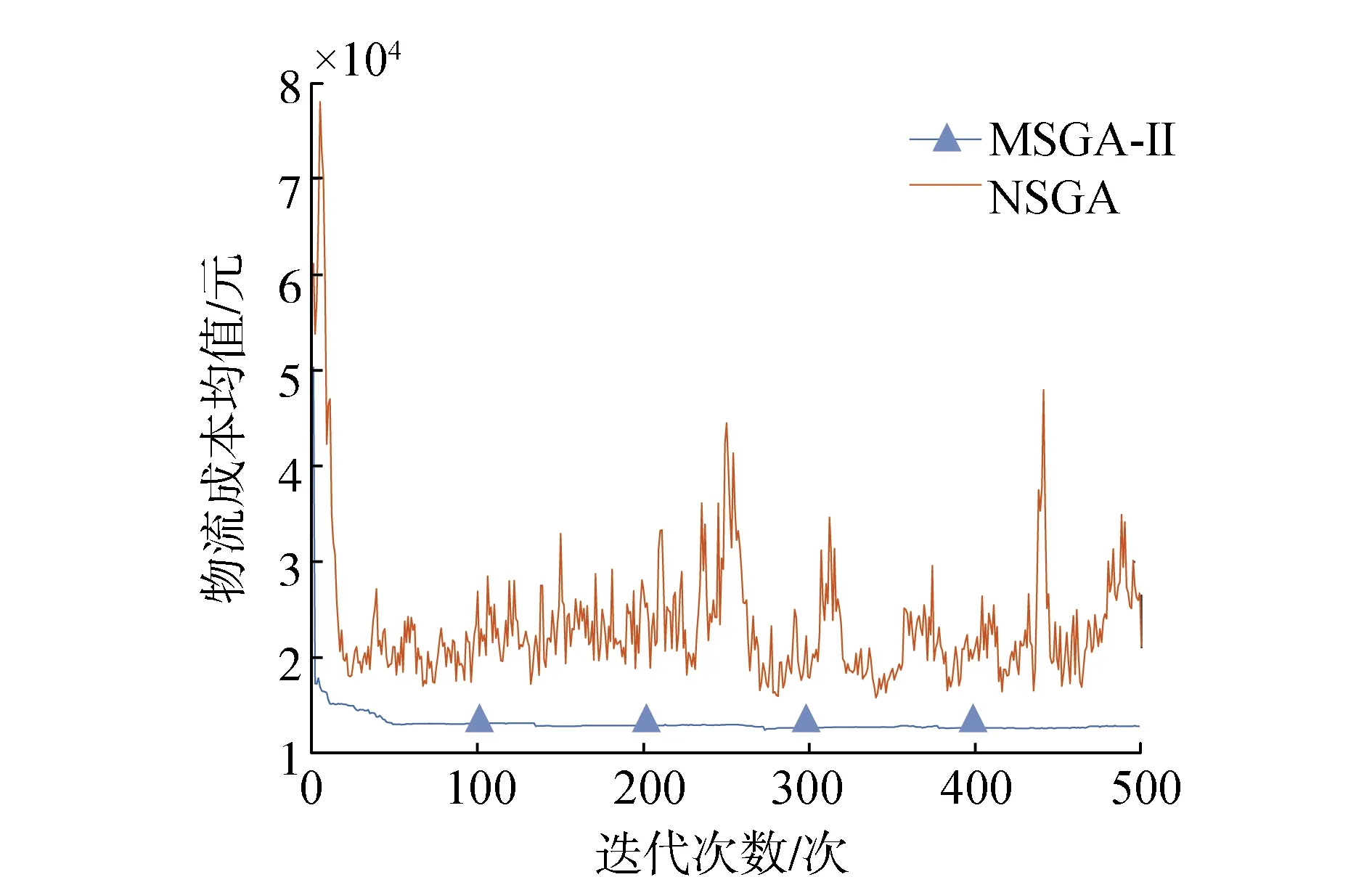
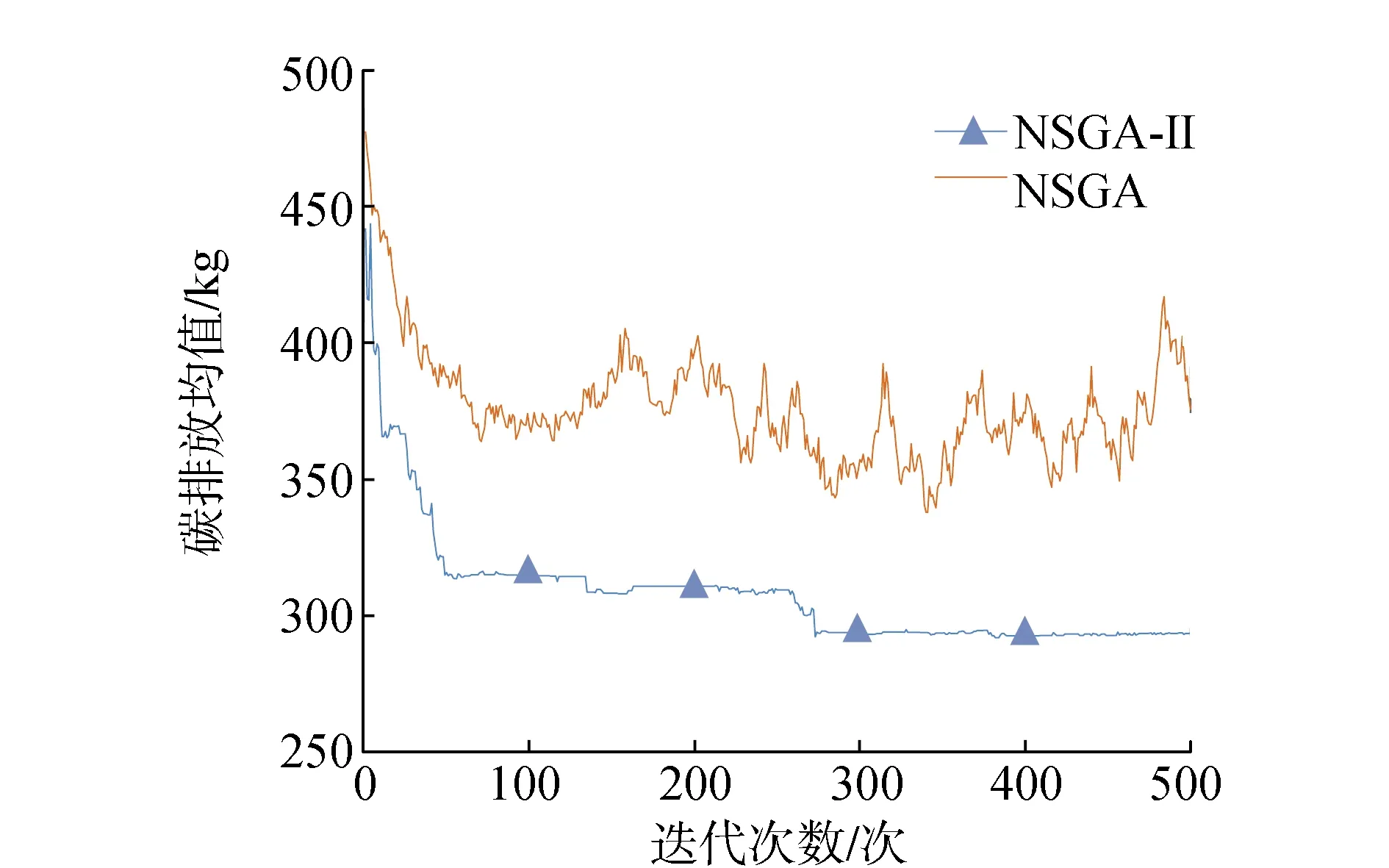
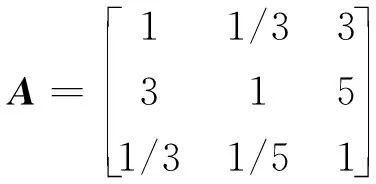
为确保所有解集能够收敛到一个均匀分布的Pareto面上,需要一个比较优劣的选择算子。选择算子能够避免优良染色体的损失,增加高性能的个体生存概率,从而提高全局收敛性和计算效率[22]。经过快速非支配排序和拥挤度计算的个体,都拥有非支配排序等级krank和拥挤度kd两个属性,二者为选择算子。定义偏序关系:当krank 选择操作采用锦标赛选择策略,即每次从种群中随机取出2个个体,根据偏序关系,选择较优个体进入子代种群,并重复该操作,不断选出较优个体,直到规模达到原种群规模[23]。 步骤6 交叉操作 经过选择操作得到的较优群体,需要以概率Pc完成交叉操作。由于每条染色体均为全排列,在交叉过程中仍要保证其有效染色体特性,对染色体进行以下交叉操作: 1)在选择得到的群体中,随机选择2个个体,并随机选择相同的交叉区域,例如:A=362|95810|174,B=587|49106|312; 2)将B的交叉区域复制到A的前面,将A的交叉区域复制到B的前面,得到:A′=|49106|36295810174,B′=|95810|58749106312; 3)在A′、B′中删去交叉区域后重复的自然数,得到:A″=49106325817,B″=95810746312; 4)对新产生的子代A″和B″重新进行有效染色体判断,若均不存在超载,则视为有效子代,否则重新交叉。 通过交叉操作,染色体片段被重新组合,推动了多种群的多样化发展。 步骤7 变异操作 变异操作与交叉操作同时进行,变异概率为Pm。由于染色体编码的特殊性,在变异过程中不能生成新的自然数,否则会产生无效变异,无法完成染色体解码,因此,为保证染色体的全排列特性,并保证其有效性,规定染色体的变异方式为:随机选择一条染色体,C=36295810174,在染色体上随机选择两个位置,如C=362|9|5810|1|74,将两个位置上的数字进行互换,得到新的染色体C′=36215810974,对新生成的子代进行有效染色体判断,若不存在超载,则视为有效子代,否则重新变异。 步骤8 精英策略 精英策略可以保证上一代种群中优秀个体进入子代,它是遗传算法以概率1收敛的必要条件。图4为NSGA-II算法的主要流程。 图4 NSGA-II算法流程 首先,初始化父代种群P0,种群大小为N,先进行非支配排序和拥挤度排序,再进行选择、交叉、变异操作,产生下一代种群Q0,设R0=P0∪Q0,利用R0完成以下操作: 1)将第t代产生的子代种群Qt和父代种群Pt合并成Rt,种群大小为2N; 2)对Rt进行快速非支配排序形成非支配集F1,F2,F3…,再对同一非支配级的个体进行拥挤度排序,选择此时Rt中的前N个个体作为父代种群Pt+1,其余个体删去; 3)对父代种群Pt+1进行选择、交叉、变异操作,产生子代种群Qt+1; 4)重复操作1)—3),直至达到规定的最大代数[24]。 通过NSGA-II计算可得到Pareto解集,对Pareto解集中的方案进行无量纲化,可得到决策矩阵B=(bij)p×q,经过层次分析法可得到目标的权重向量W=(w1w2…wj)T。因此,评价方案的满意度矩阵可表示为 (27) 最终选择的方案DL可表示为 DL=max{Di} (28) 为验证算法的有效性,以华北地区某省的实际情况作为参考,随机生成需求点,进行算法模拟。该配送中心负责周边50 km以内的生鲜农产品配送,现有一笔订单,为分布在各地的20个客户配送水果,客户分布如图5所示。各客户的位置、需求量、期望时间窗等信息如表1所示。 图5 配送中心及客户位置分布 表1 客户需求信息 水果从产地运往配送中心,消耗时间默认为T0,考虑从配送中心到客户的运送过程,故T0取0。不考虑由于交通拥堵导致车辆行驶速度改变的情况,车辆以50 km·h-1均速行驶,每辆车的固定成本为200元·辆-1,车辆的最大载重量为7 t。假设配送过程中车内温度控制在6 ℃,车外温度为21 ℃,α1和α2的取值为算例合理假设,可根据具体情况进行调整,其他参数如表2所示。 表2 参数设定值 利用MATLAB对算法进行求解,以Aravind Seshadri在MathWorksk中提出的NSGA-II代码为参考,修改编码方式,将文中的二进制编码方式改为适合本文的自然数全排列编码方式,并对各流程进行相应修改,初始群体、交叉操作和变异操作时均考虑染色体的有效性。 3.2.1 NSGA-II初步求解算例 种群为50,交叉概率为0.95,变异概率为0.05,采用NSGA-II进行500代计算,运算时间为72.91 s,50个Pareto解的三维立体图如图6所示。 图6 NSGA-II求解的Pareto面(500代) 通过图6可以看出50个点几乎落于同一面——Pareto面上,说明收敛效果较好,每个点对应的解几乎都是最优解。 为说明NSGA-II的优势,利用NSGA与其进行对比,通过运行得到NSGA运算时间为NSGA-II的4倍左右,把2种算法500代中各代排序前10的个体目标函数的平均值变化过程以曲线表示,如图7—图9所示,比较2种算法的优劣。 图7 客户满意度均值变化 图8 物流成本均值变化 图9 碳排放量均值变化 从图7—图9可以看出,NSGA-II的客户满意度均值明显高于NSGA,碳排放均值明显低于NSGA的碳排放值,物流成本可以实现快速收敛,物流成本均值维持在12 800元左右。由于NSGA所得结果的波动比较大,不像NSGA-II可以实现快速收敛,所以,利用NSGA-II算法进行求解具有一定的合理性和有效性。还可以看出NSGA-II所得结果的碳排放量在300代后波动较小,碳排放量均值维持在294 kg左右。而客户满意度则在小范围内不断波动,均值在98.5%左右,为追求较少的物流成本和碳排放,需要牺牲一定的客户满意度。 3.2.2 无量纲化处理Pareto解 将NSGA-II计算得到的Pareto解集进行无量纲化处理,将各个目标值均变换到范围内,统一量纲。文中采用以下量化处理方式。 1)对于正向指标(客户满意度)进行如下量化处理 (29) 2)对于负向指标(物流成本、碳排放量)进行如下量化处理 (30) 经过无量纲化得到方案的决策矩阵B=(bij)p×e。 3.2.3 AHP决策过程 通过专家打分或合理性假设得到判断矩阵,即对客户满意度、物流成本、碳排放量三者的重要性进行量化处理,采用专家打分法对三个目标的重要程度进行评判。本算例对各目标重要程度进行合理性假设,方便对算例结果进行选择。实际问题需根据实际情况进行专家评判。 实例决策时重要性依次为物流成本、客户满意度、碳排放量。在碳达峰、碳中和双碳目标下, 碳排放越来越受到重视,但相比于客户满意度与物流成本其重要性仍较小,而成本是最被关注、最为重要的目标,其重要性较大,用1~9之间的数据来表示它们之间的两两重要性。算例得到的判断矩阵为 经计算得到权重向量:W=(0.258 3 0.637 00.104 7)T。 3.2.4 综合评判 利用式(27)可得到评价方案满意度矩阵,并在方案中选择最大值DL,得到DL=0.668 5=D38,说明方案38为最满意方案,客户满意度为97.71%,物流成本为12 359.13元,碳排放量为291.62 kg,具体配送路线如表3所示。 表3 最满意方案配送路线 1)冷链物流配送过程中,为保证生鲜农产品的新鲜度,需增加制冷成本,由此产生高成本与高碳排放,混合时间窗下客户对产品送达时间存在约束,配送过程中各个目标存在效益背反关系。文中以客户满意度(生鲜农产品新鲜度和准时送达率)最大化、物流成本(固定成本、变动成本、制冷成本和时间窗惩罚成本)最小化、碳排放量(运输能耗和制冷)最小化为目标,在车辆最大载货量、配送连续性和混合时间窗约束下,建立冷链物流配送路径多目标优化模型。 2)针对多目标问题,采用NSGA-II求解,根据冷链物流配送路径特点,进行染色体全排列编码,以载重量限制作为染色体有效性检验的依据,在交叉和变异时仍保持全排列特性,并用精英策略保留父代精英解。经过NSGA-II计算得到Pareto解集,并进行AHP决策,选出最优满意解。 3)进行算例验证,并与NSGA求解方法对比,以服务20个客户为例,利用MATLAB进行求解,将第500代的父代结果作为最终的Pareto解集,并分析各目标均值变化过程,将NSGA与NSGA-II运算结果对比,发现利用NSGA-II求解收敛速度较快,且结果质量较高。经过AHP决策选出的最优满意解,各目标值较为理想,证明了该模型和算法的有效性与实用价值。
2.2 AHP决策
3 冷链物流配送算例
3.1 算例说明
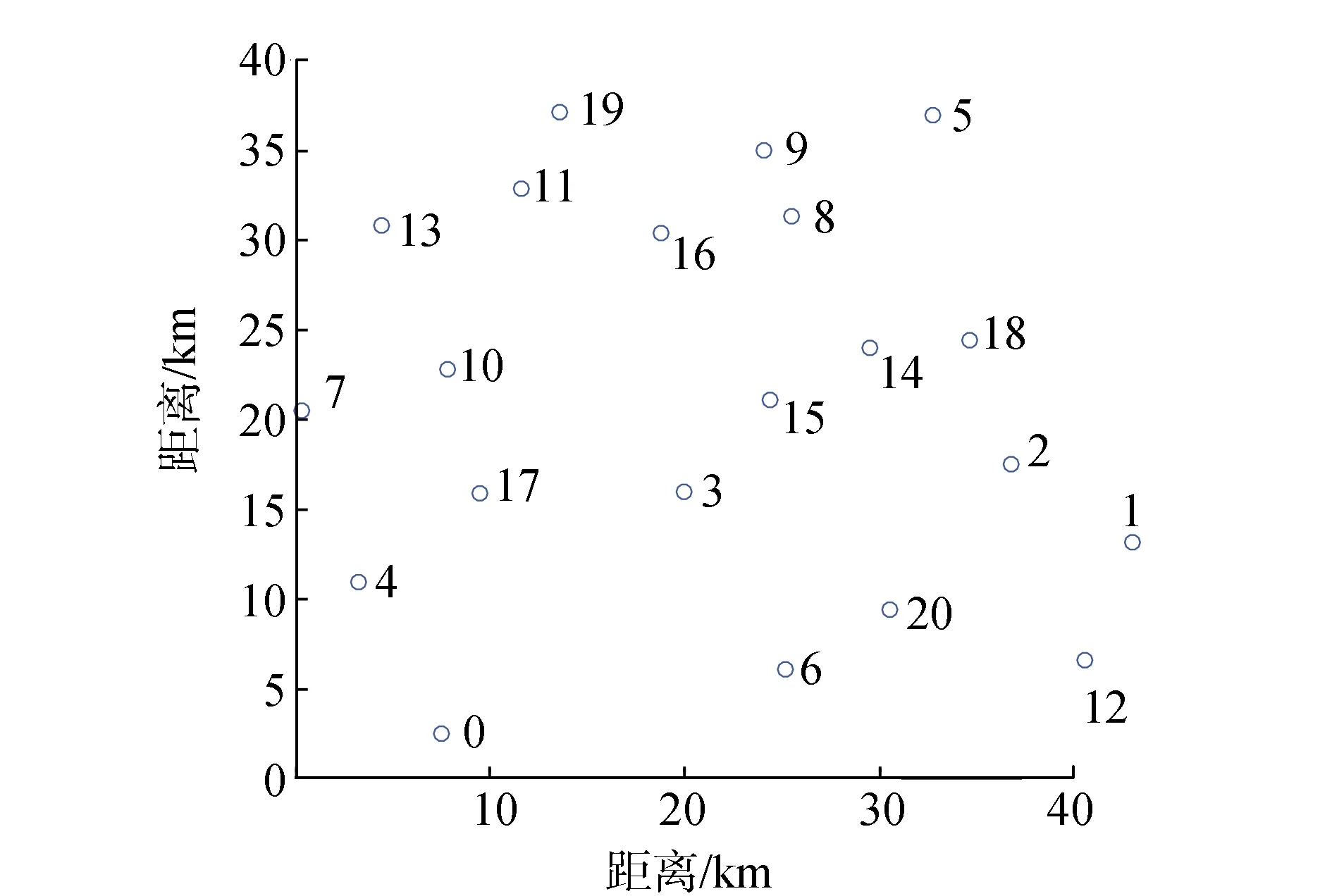


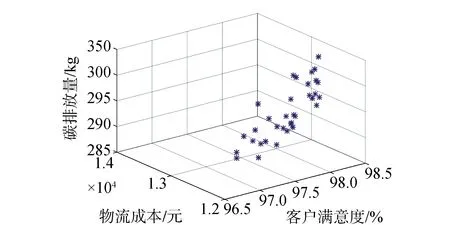
3.2 算例结果分析
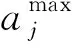

4 结 论
