基于多尺度有限元的海上升压站脚靴式桩套筒连接结构分析研究

张 伟，张 坤，姜贞强，孙震洲，王永发，吕国儿，陈杰峰

(1.华能辽宁清洁能源有限责任公司，辽宁 沈阳 110000；2.浙江省深远海风电技术研究重点实验室，浙江 杭州 311122；3.中国电建集团华东勘测设计研究院有限公司，浙江 杭州 311122)

随着“3060”碳排放目标的提出，作为可再生清洁能源的海上风电将迎来持续性的增长。截至2021年年初，国内已成功建设40余座海上风电场，在建海上风电场20余座。在海上风电场从浅海向深海发展的大趋势下，承担电能汇集及传输作业的海上升压站结构型式由桩插入主导管型式向桩插入水下套筒型式转变。一方面，桩—套筒脚靴式导管架可大大降低导管架钢材量；另一方面，该导管架型式海上打桩、灌浆等施工更为简便，大大提高了工程经济性。相应地，脚靴式连接结构扮演着荷载从导管架向桩基础传递的重要角色，一旦失效将造成灾难性后果。因此，针对上下轭板、剪力板等连接件开展更精确地计算方法研究分析，是该型式海上升压站在位状态安全性评估的关键。

现有的工程设计中，通常采用有限元计算软件建立整体海上升压站的框架结构模型，关注梁、杆等单元的应力状态。对于脚靴式结构与主导管的连接部位，其由剪力板、上下轭板及翼缘板等板型结构构成，在梁杆系有限元中无法准确计算板的应力状态[1]。因此针对关键部位的板型结构，通常采用截断的板系有限元模型进行计算分析。然而，截断有限元模型对于边界条件设置十分敏感，不准确的边界条件可能造成截然相反的结论。此外，对于海上升压站，其设计工况包含在位[2]、地震[3]、靠船[4]、疲劳[5]等诸多控制性工况，截断有限元模型需要提取大量组合工况的节点位移、荷载等边界条件，同时涉及整体坐标系与局部坐标系的转换，给设计人员增加了巨大的计算复核压力。

为解决整体有限元与截断有限元之间的矛盾，宜采用多尺度有限元同步模拟宏观的整体行为及结构局部的微观特性[6]，在保证计算效率的同时，也可提高局部区域的计算精度[7]。对于多尺度有限元的研究，国外起步较早。在20世纪末，McCune等[8-9]基于功平衡原则给出了梁单元—实体单元、梁单元—板单元等跨尺度界面的节点约束方程，该方程具有更好的应力连续性的同时，考虑了杆件的剪切变形效应。随后，Nukala等[10]将多尺度推广至框架结构中，解决了几何非线性问题；Ladeveze等[11]在多尺度域分解方法的基础上，增加了时空多尺度特性，发展了广义分解法。除结构多尺度外，Fafitis[12]通过多尺度有限元模型，对材料非线性开展研究并验证了跨尺度耦合的可行性；Li等[13]提出了一致多尺度方法，对材料损伤演化造成的结构失效进行模拟，分析了强动荷载引起的结构失效问题。

目前，国内学者也对多尺度有限元开展了诸多研究。李兆霞等[14]基于ABAQUS软件，研究了大跨结构多尺度模拟中的建模方法和策略；刘海峰[15]研究了网格节点或杆件塑性屈服前后，多尺度有限元求解的弹性阶段和塑性阶段；徐世鹏[16]针对粗糙边界问题，采用局部正交分解技术构造了多尺度组合有限元法；郑哲远[17]提出了尺度域演变机制，并建立了边尺度域有限元方法，解决了损伤跨尺度演化对计算精度的影响；王小庆[18]通过优化改进的多尺度并行数值模拟方法，将多尺度计算推广至千万自由度以上的超大规模数值分析。可以看出，针对海洋工程结构特别是海上风电结构的多尺度模型分析研究尚少，同时有限元结果仅针对屈服强度的验算，无法完成板受压时的屈曲极限复核，对于短、频、快的海上风电结构工程设计未形成指导性意见。

文中基于多尺度有限元计算理论及SACS软件，针对我国东北地区某海上风电场的脚靴式海上升压站结构，建立多尺度有限元模型，对脚靴结构的屈服强度进行复核；并采用直接计算的方式，对各板件的屈曲进行验算。同时，通过不同精细化范围的多尺度有限元模型及不同边界的截断有限元模型对比研究，论证了多尺度有限元的优越性，给出了截断有限元边界条件设置建议；进而结合屈曲极限的敏感性曲线，为工程设计的不同阶段提供建议。

1 失效模式分析

1.1 屈服失效

在工程应用中，通常可采用有限元计算中的等效应力来研究所关注结构的屈服强度。文中采用多尺度有限元法来确保边界条件及传力路径的准确性，以计算得到较为可靠的设计强度值。

多尺度有限元分析中，通常将结构分成两个部分——整体大尺度域Ω(1)和局部小尺度域Ω(2)。基于最小势能原理，为得到位移的唯一解，应使得系统应变能的变分为零，可以得到有限元的一般控制方程，同时对应于多尺度有限元模型不同尺度域，可表达为：

(1)

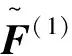
(2)

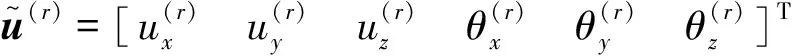
(3)

式中：F及M为梁/杆单元的节点力及力偶；Nd为跨尺度界面上精细化单元的数量；Ai为精细化单元的面积；τ为单元平面内的剪应力流；σ为主应力；α为单元局部坐标系与整体坐标系的夹角，上标e代表单元。

1.2 屈曲失效

对于轭板，其结构型式属于外沿受压构件，其受压屈曲应满足[19]：

(4)

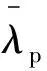
(5)

其中，s为板的宽度，t为板的厚度，kσ为屈服强度fy的折减系数，其与板两端的应力比Ψ存在一定的函数关系，即kσ=f(Ψ)，两者关系如图1所示。实际计算时，Ψ应根据有限元计算得到的轭板两端应力关系确定，Ψ=σ2/σ1，σ1为较大侧应力的最大值，其中受压为正。从图1可以看出，当最大应力位于约束侧时，kσ对应力比Ψ十分敏感。因此，为保证屈曲校核的准确性，应尽可能地在有限元计算中计算得到准确应力比Ψ。

图1 kσ与Ψ关系图[19]

对于轭板受剪、剪力板受剪屈曲校核及轭板翼缘的校核，可参照规范DNV-RP-C201[19]，文中不做赘述。

对于屈服和屈曲校核，可采用UC(unity check)值来直观衡量结构的安全性，对于安全性复核时，UC值应满足以下要求：

(6)

式中：σmises为采用多尺度有限元模型计算得到的等效Mises应力，γm为材料系数。

2 工程算例

2.1 计算模型

文中所采用的计算模型依托于大连海域某300 MW海上风电项目海上升压站。该海上升压站上部组块采用空间桁架结构，平面尺寸约41.0 m×38.0 m，共设置4层甲板，总高度约20.5 m，一层为电缆层及休息区，主变压器、气体绝缘组合电器(GIS)、开关柜等主要设备布置于2～4层，总质量约3 200 t。基础采用桩—套筒脚靴式导管架结构，脚靴处主导管腿截面尺寸为Φ1 850 mm×50 mm，套筒截面尺寸为Φ2 960 mm×50 mm，两者通过上、下轭板及剪力板焊接连接。算例工程桩径为2 600 mm，入泥约49 m，桩基持力层为粉质黏土层。

海上升压站所处海域平均海平面水深为23.22 m，选取具有代表性的极端风暴潮工况作为研究工况。其百年一遇高潮位为3.79 m，百年一遇低潮位为-4.14 m，百年一遇最大波高为Hmax=3.09 m，其对应周期T=9.44 s，百年一遇最大垂向平均流速为1.41 m/s。为精确计算桩—套筒处位置板的应力状态，采用SACS V15.0进行多尺度有限元建模。为同时保证计算效率，通过无局部细化的有限元模型试算后，选取最危险受力处的脚靴式连接结构，采用板壳单元对主腿及其相邻撑杆、套筒、剪力板、上下轭板及轭板翼缘板进行网格划分，各构件参数如表1所示。为体现撑杆与主腿的节点关系并获得最优的网格质量，撑杆及主腿采用三角形单元，其余位置均以四边形单元为主，最终计算模型如图2所示。特别地，局部精细化建模位置波流力无法直接采用Morison公式计算得到，为保证荷载输入的正确性，通过调整板的拖曳力系数，使环境荷载等同于无局部细化的整体模型环境荷载。

图2 海上升压站的多尺度有限元计算模型

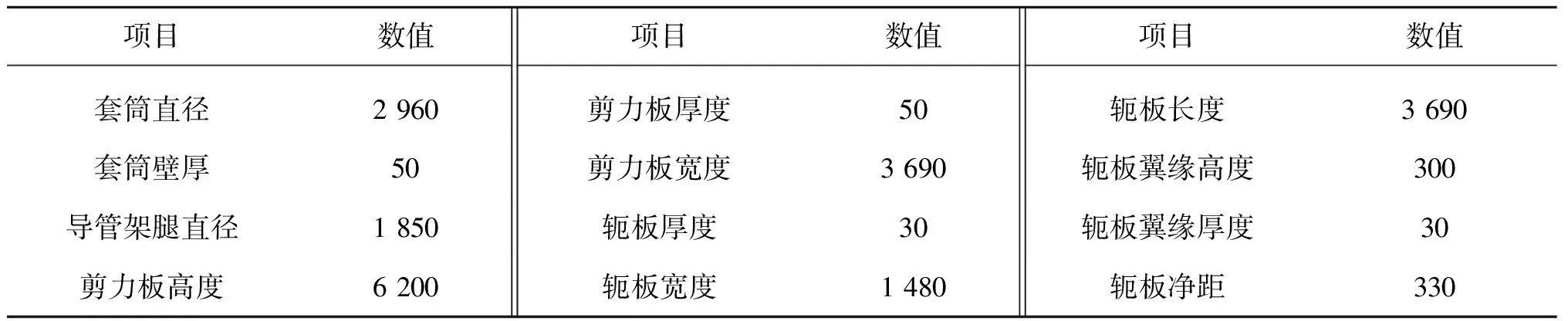
表1 脚靴式连接结构各构件参数 Tab.1 The parameters of the boot-type substation (mm)

2.2 屈服失效分析

多尺度有限元模型约束条件等同于在位工况时整体有限元模型的约束，即套筒底部为土体超单元矩阵。极端风暴潮工况计算时共设置32组工况，包括各个典型角度的风浪流荷载组合，如表2所示。为保证多尺度有限元模型中计算结果的可对比性，选取局部小尺度域处的桩头0779位置，对比计算得到的桩头水平位移及桩头轴力结果，如图3所示。可以看出多尺度模型与整体模型计算结果基本吻合，验证了多尺度模型局部精细化建模的合理性。

表2 极端风暴潮荷载工况组合

图3 多尺度有限元与整体有限元节点位移及内力对比

通过桩土非线性静力分析，可得到海上升压站大尺度杆件UC结果及小尺度板等效应力结果，如图4所示。不难看出，上部组块及导管架各梁、柱和杆件UC值均小于1，满足安全性要求。需要指出，对于局部精细化模型，其主腿撑杆可直接通过杆件校核结果得到，因此撑杆的网格划分仅为得到主腿应力分布及撑杆与弦杆交界处网格的连续性，不作为应力校核的参考依据。

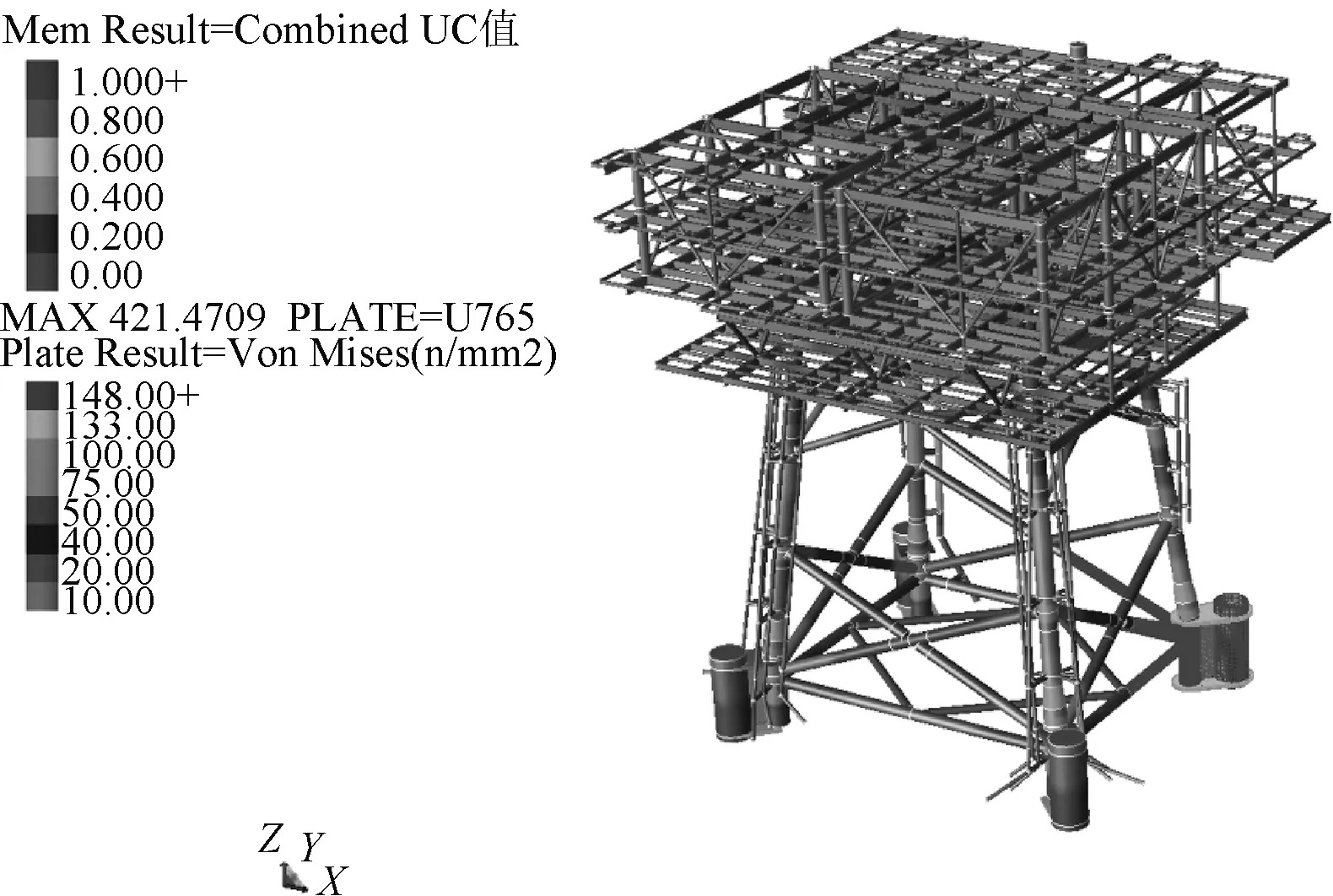
图4 多尺度有限元6012工况计算结果

多尺度有限元中各板的等效应力云图如图5所示。在局部精细化模型中，对套筒—浆体—桩的相互作用予以忽略，保守考虑该位置板单元厚度仅为套筒壁厚，通过改变套筒单元板的密度来修正缺失的桩及灌浆料质量，该部分的局部强度及浆体的抗剪/压强度需额外计算[20]。通过多尺度有限元计算得到最大等效应力位于剪力板与套筒、下轭板连接处，幅值达到421.5 MPa。该位置处于应力重分布的交界处，具有明显的应力集中现象，且该位置塑性应变小于5%，不会导致塑性区域进一步扩展。基于规范[21]，考虑1.15材料系数的50 mm钢板的屈服强度为282.6 MPa，除应力集中位置外，最大等效应力215 MPa小于板的屈服强度，满足安全性要求。另外，上、下轭板及其翼缘介于75～181 MPa间，最大等效应力为180.4 MPa，位于剪力板与下轭板连接处，同样满足安全性要求。

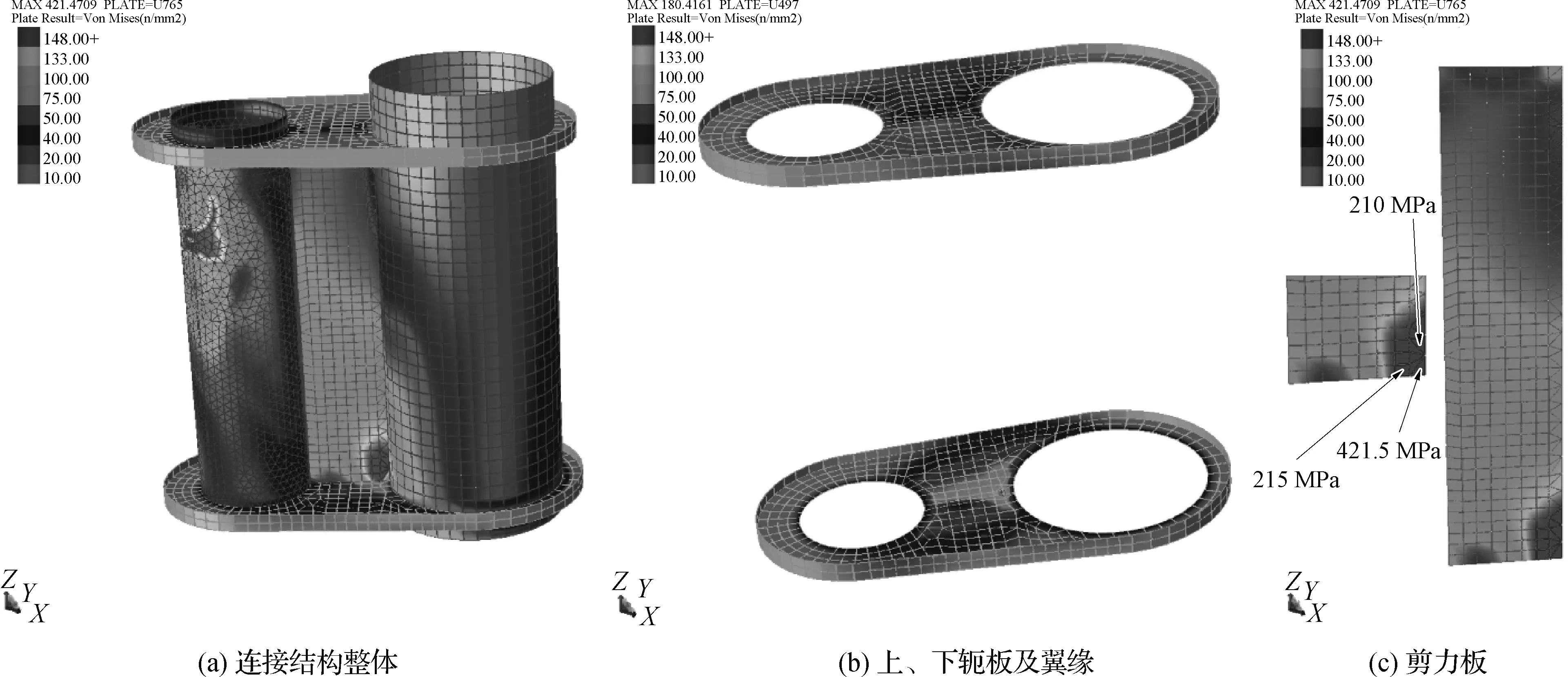
图5 脚靴式连接结构等效应力云图

2.3 屈曲失效分析

对脚靴式连接结构上、下轭板及剪力板屈曲校核时，为保守考虑通常假定桩头传递的基底弯矩和剪力均由轭板承担，桩头传递的竖向力则由剪力板承担。基于轭板及剪力板的受压状态，轭板按外沿受压构件进行屈曲校核，剪力板按无加强筋受剪构件进行屈曲校核。在轭板的屈曲校核时，建立如图6所示的局部坐标系，将基底弯矩及剪力转换至轭板所在的局部坐标系中进行校核，x方向为导管架中心与桩中心连线方向，y方向垂直于该连线方向，剪力板屈曲校核仍采用整体坐标系。

图6 轭板局部坐标系

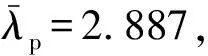
从脚靴式连接结构的两种失效模式分析中可以看出，对于算例工程极端风暴潮工况，剪力板的屈服失效为最危险工况，UC值达0.76，且上轭板的屈曲UC值(0.63)相对于屈服UC值(上轭板最大等效应力为168.9 MPa，UC值为0.60)更大，说明了仅屈服校核无法涵盖所有失效模式，表明屈曲校核的必要性。

3 有限元模型敏感性分析

对多尺度模型精细化范围及截断模型边界条件对于结果的敏感程度进行分析，特别地，选取桩头产生最大竖向荷载的6012工况(低水位下重力起主导作用时和45°环境荷载的组合工况)。在海上升压站整体坐标系下，该工况桩头(0779)位置内力为FX=2 741.1 kN，FY=2 971.9 kN，FZ=-15 960.9 kN，MX=21 468.2 kN·m，MY=-20 900.8 kN·m，MZ=-101.7 kN·m，以用于截断有限元该位置的边界条件约束。

3.1 多尺度模型精细化范围

从2.2节计算结果可知，项目结构主导管并非为最危险位置，在多尺度有限元模型中，为了保证主导管与撑杆相贯关系，在其局部位置需划分大量网格，降低了运算效率。这里建立无撑杆网格划分的多尺度有限元模型为对比模型，大大降低网格数量和网格复杂程度，讨论多尺度模型精细化范围对计算结果的影响。

为保持计算结果的可对比性，模型除不对撑杆进行网格划分及主腿采用四边形单元网格划分不同外，其余网格划分及输入条件设置均保持一致。最终计算结果对比如表3所示，各部位等效应力云图如图7所示。可以看出，除主导管位置外，其余部件最大等效应力均有所增长，但均在10%以内，等效应力云图趋势均保持一致。主导管位置由于撑杆荷载传递由网格传递更改为杆件节点传力，局部网格位置的受力无法体现，被网格所耗散的荷载变小，进而导致其余构件等效应力变大。因此，若在设计前期或关注重点为连接构件时，可不对撑杆节点网格划分，提高计算效率的同时，使得计算结果更为保守，有利于前期结构设计。

表3 不同精细化范围多尺度模型计算结果对比

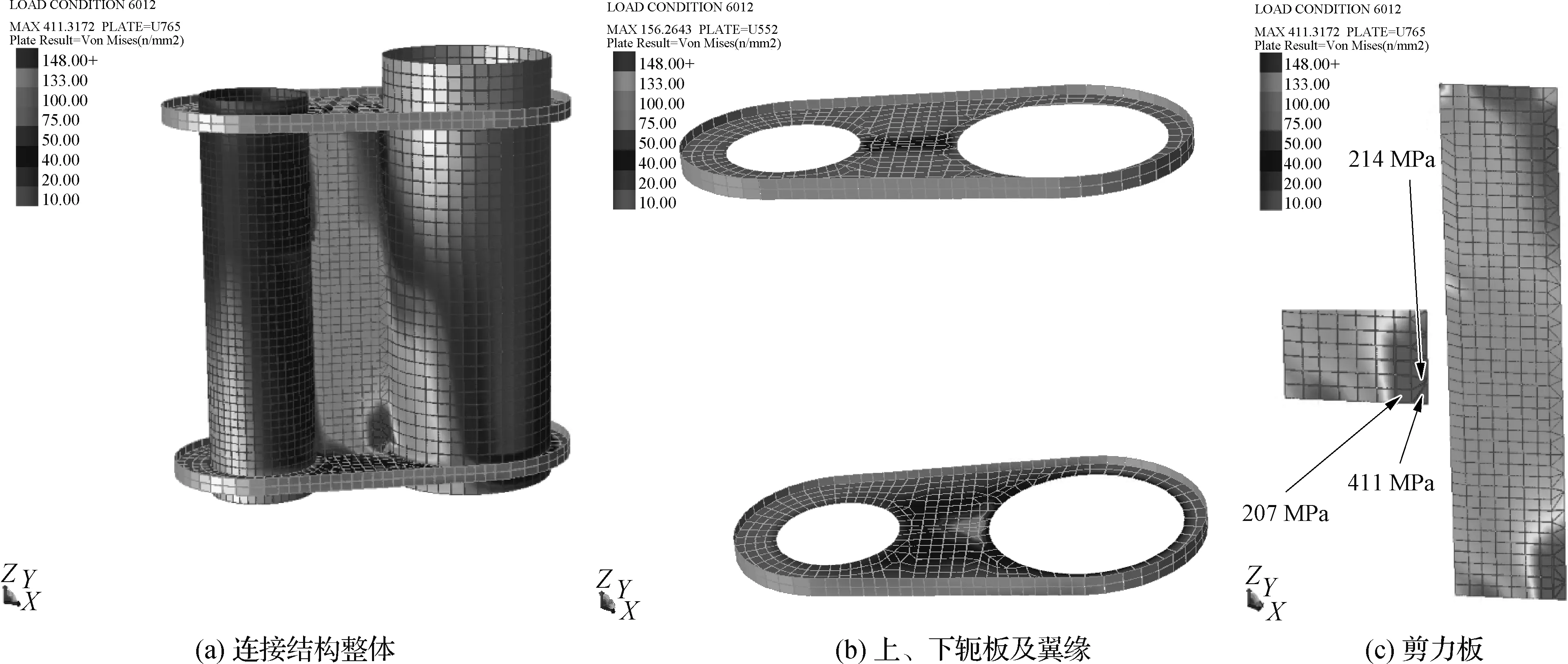
图7 脚靴式连接结构精细化范围缩小等效应力云图

3.2 截断模型边界条件

通过设置6组不同截断有限元模型的边界条件，研究计算结果对边界条件的敏感程度。同样为消除有限元网格带来的影响，截断模型采用2.2节多尺度有限元模型中精细化建模部分。相同的，为结果显示的清晰性，同样不对撑杆进行应力分析。6组边界条件设置如表4所示。

表4 截断有限元模型边界条件设置

计算得到各截断模型等效应力云图如图8～13所示。其中，截断模型4和截断模型5由于等效应力超限大，采用百分比的形式来体现应力分布。基于3.1节结论，这里重点关注上、下轭板及剪力板的等效应力幅值变化，结果汇总于表5中。通过结果对比，可以得到如下结论：

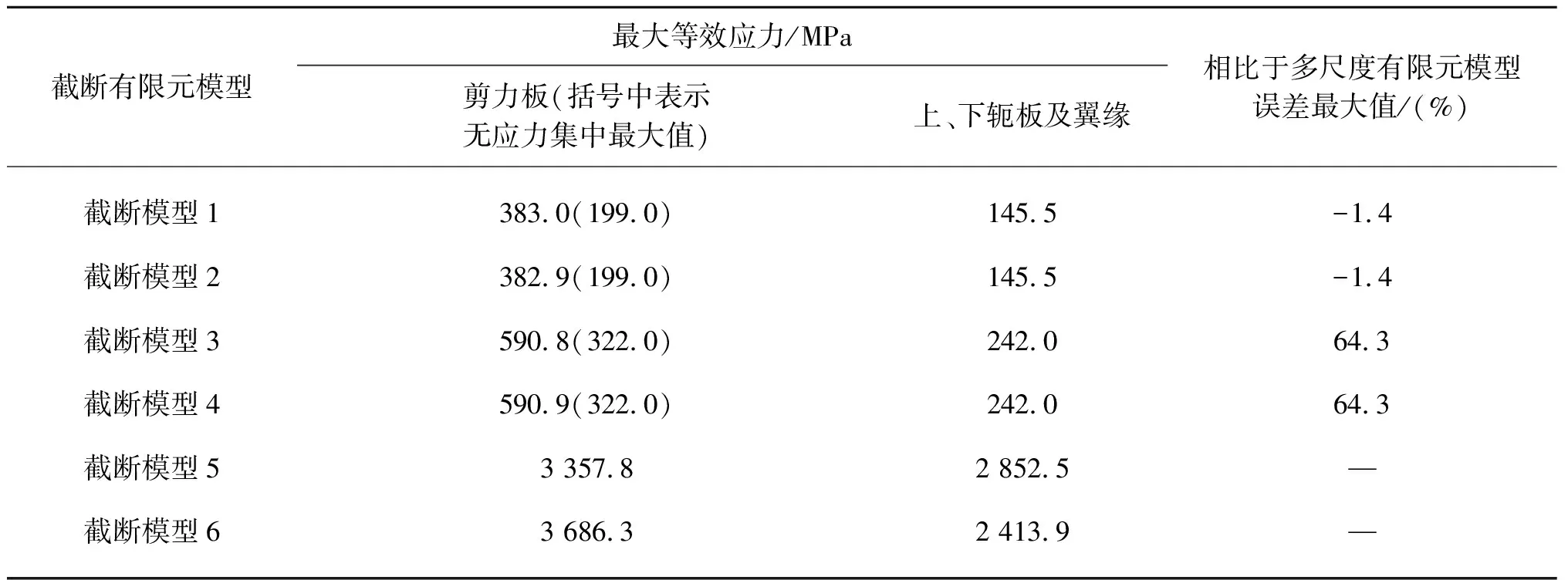
表5 截断有限元模型计算结果

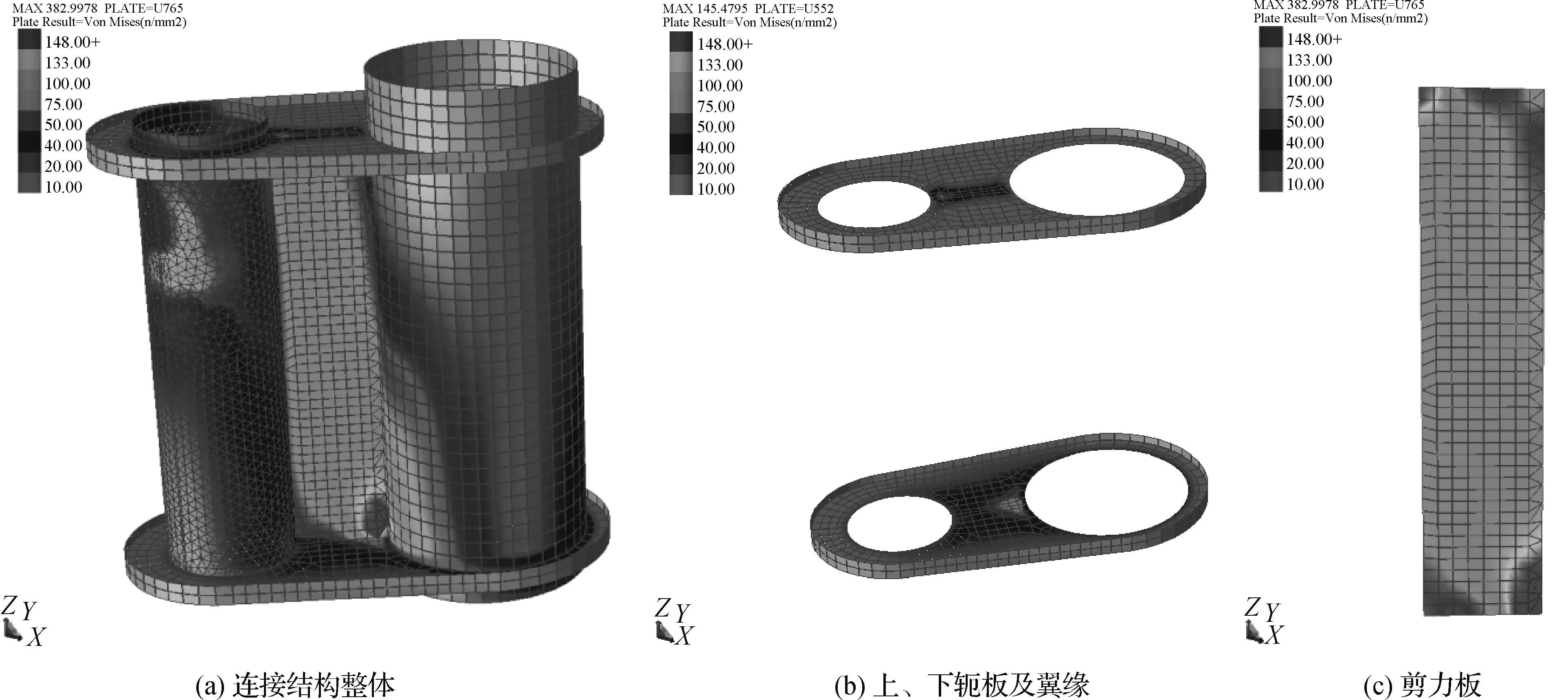
图8 截断模型1等效应力云图计算结果

1)各截断有限元模型中，剪力板的等效应力分布基本一致，极值点均出现在剪力板与下轭板、套筒和上轭板、主导管连接位置，且下方等效应力更大，截断模型1和截断模型2与多尺度模型计算结果更为接近；

2)相比于多尺度模型，截断模型1和截断模型2上、下轭板等效应力最大值基本相同，但除开最大等效应力位置，如轭板边缘及翼缘计算结果整体偏小；

3)从主导管的应力分布可以得知，截断模型1与截断模型2相比，其结果更接近多尺度有限元模型，因此在不便于提取撑杆位移时，可简化采用固定约束进行分析，但需注意主导管的校核结果将偏危险；

4)套筒底部施加固定或位移约束后，计算结果均偏大，这是由于在多尺度模型中，套筒底部实际是采用桩土相互作用产生的约束，等效刚度较小。截断面的约束越强，则计算得到的等效应力结果越大。

综上，在截断有限元分析计算时，推荐采用截断模型1的约束方式；当主导管构件应力水平低或多尺度模型截断位置节点位移获取困难时，可采用截断模型2来分析。但针对上、下轭板翼缘的校核，截断模型结果均偏小，若该位置为主要关注位置，应采用多尺度有限元模型或相应规范条款进行补充分析。

图9 截断模型2等效应力云图计算结果

图10 截断模型3等效应力云图计算结果

图11 截断模型4等效应力云图计算结果

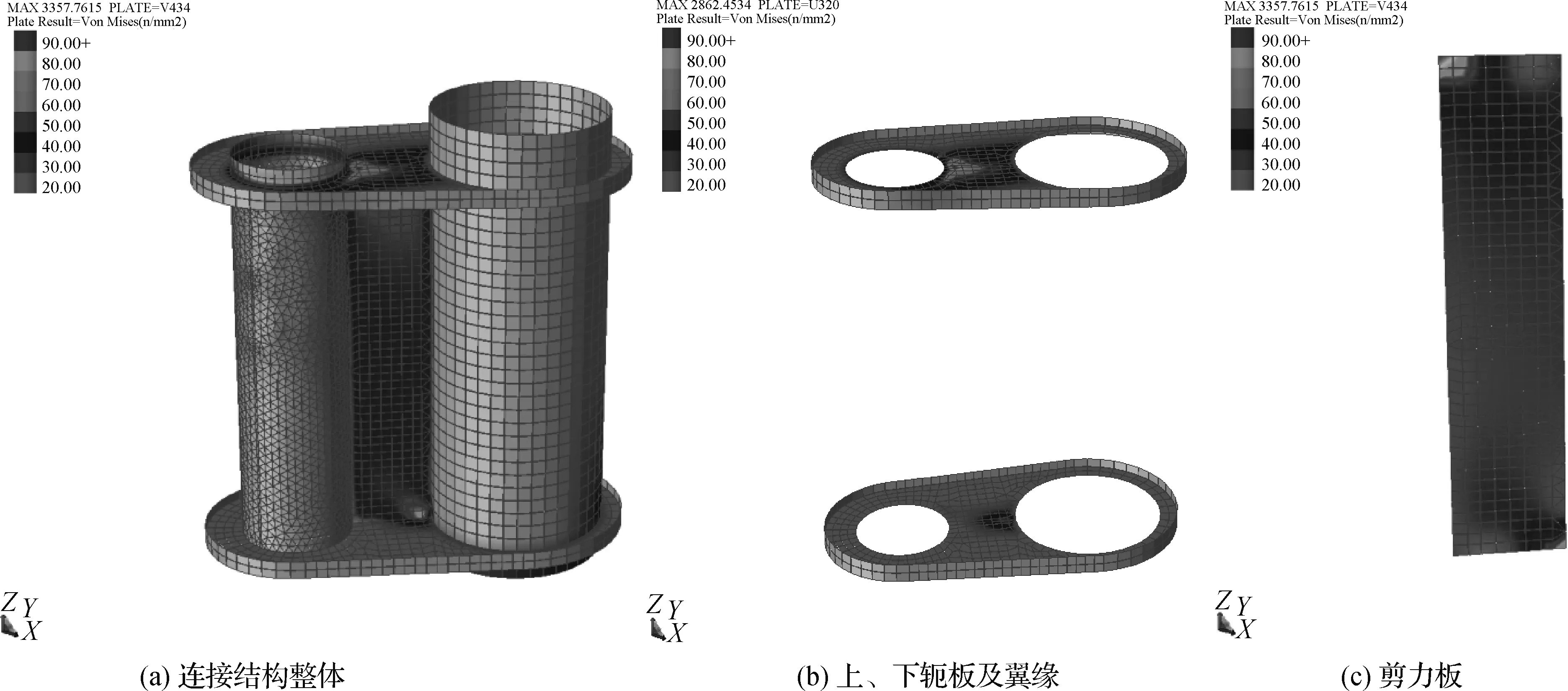
图12 截断模型5等效应力云图计算结果

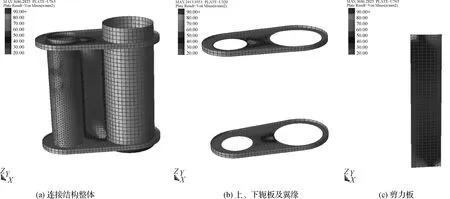
图13 截断模型6等效应力云图计算结果

4 屈曲敏感性分析

4.1 结构设计参数

根据2.3节结论，对于文中工程项目剪力板的控制工况为屈服失效，屈曲UC值较小，但上轭板的屈曲UC值要大于屈服UC值，因此将探讨不同轭板板厚对屈服及屈曲设计的敏感性。为保证轭板屈服应力计算结果的准确性，重点关注轭板的等效应力值，因此基于3.1节结论，采用无斜撑的多尺度有限元模型进行保守计算，同时为排除应力比对屈曲极限的影响，均选取30 mm轭板计算的应力比0.78计算，共考虑32组工况。分别设置轭板板厚为20～40 mm，板厚间隔为5 mm，计算得到的两种失效模式UC值如图14所示。

从图14中可以看出，屈曲UC值随轭板板厚变化斜率更大，即屈曲失效对轭板板厚更为敏感。对于工程中当板厚为30 mm时两种失效模式UC值相当。在工程设计中，除构件安全性校核需求外，仍需考虑钢材用量、焊接施工难度等，当板厚提高时，焊接难度及用钢量增加明显。可综合考量项目需求、施工质量及安全性等指标，给出合理的板厚设计值。

图14 轭板板厚对失效模式的影响

4.2 应力比Ψ

脚靴式连接结构上轭板的屈曲不仅与本身设计参数有关，亦与应力比Ψ关系密切。基于规范[19]要求，应力比应根据有限元计算结果确定，因此从不同有限元模型计算得到的应力比Ψ对屈曲计算的敏感性，来探讨多尺度有限元模型的优越性。

选取6012工况为研究工况，基于3.2节的结论，对两个多尺度有限元模型及截断模型1～6进行分析研究。根据公式(5)，可以绘制出屈曲极限折减系数Cx与应力比Ψ的关系，如图15所示，可以看出在不同约束条件下，折减系数均随着应力比的增大而减小，当应力比为1时达到最小值0.30。对于文中工程，可以计算得到带斜撑的多尺度模型应力比为0.78，不带斜撑的多尺度模型、截断模型1和2的应力比为0.60，截断模型3和4的应力比为0.58，屈曲极限值分别为93.20 MPa、102.31 MPa和103.33 MPa，带斜撑的有限元计算结果最为保守，当有限元模型计算得到的等效应力结果接近时，所计算得到的应力比相当。对于工程设计的前期阶段，可采用应力比1进行保守设计；随着设计深度的提升，宜在建立多尺度有限元模型计算后，提取精确的应力比对脚靴结构的屈曲进行重新验算，以保证计算的合理性和结构的安全性。

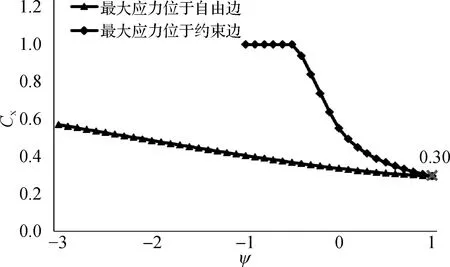
图15 屈曲极限对应力比的敏感性曲线

5 结 语

针对国内尚无多尺度有限元方法应用于海上风电场结构的空白，采用多尺度有限元方法开展了脚靴式海上升压站桩—套筒连接结构的局部分析，以某海上升压站实际结构为对象验证了其在极端风暴潮工况下屈服及屈曲失效模式的安全性。同时，开展了多尺度有限元精细化范围及不同边界条件下截断有限元计算结果对比研究，并针对上轭板板厚及应力比对屈曲极限值的敏感度分析，得到的主要结论如下：

1)对于文中海上升压站工程，脚靴式结构不存在屈服和屈曲失效，满足安全性要求。

2)多尺度有限元方法相比于截断有限元结构荷载传递更为合理，考虑桩土的相互作用，可准确计算得到脚靴处连接结构的等效应力，精细化网格面积越大，则可实现更大范围的精确等效应力计算。文中细化斜撑的多尺度模型可更为精确地计算主导管位置等效应力。

3)截断有限元模型套筒底部施加荷载边界条件及截断位置施加位移或固定边界条件时，计算结果最接近多尺度有限元结果，但在上、下轭板及翼缘位置计算结果偏危险，多尺度有限元方法计算得到的等效应力更符合工程实际，更能反映结构的受力特性；截断有限元建模边界条件建议采用荷载加位移/固定边界条件的组合。

4)脚靴式连接结构上轭板屈曲极限对板厚更为敏感，对于上轭板而言，屈曲验算更为关键；在实际工程设计时，应统筹考虑板厚、施工质量、经济性及安全性等指标。

5)在设计初期上轭板屈曲校核可保守采用应力比1进行估算，当设计阶段深入时宜采用多尺度有限元计算得到更为准确的应力比进行复核。