基于模糊认知图的气象要素预测模型

2022-04-02朱红康

计算机技术与发展 2022年3期

白雪，朱红康，吴瑞

(山西师范大学数学与计算机科学学院，山西临汾 041099)

0 引言

大气环境受到多种气象要素(风速、相对湿度、气温、气压、云量、降水量等)的综合作用，随着季节、时段、地理位置的改变，一个气象要素的变化会直接或间接地影响着其他一个或多个气象要素的变化。近来，许多学者研究发现气象要素的变化与全球灾害如干旱、山洪，人类疾病如哮喘[1]、过敏[2]、季节性流感[3]和登革热[4]等的发作和冬季供暖[5]和PM2.5[6]等造成的大气污染息息相关。因此研究气象要素间的相关性是一项重要的预防措施。目前气象要素相关性主要依靠站点检测和分析，为气象要素的预测提供数据支持。然而，气象要素之间的影响过程错综复杂，包含多种物理或化学变化过程，目前的气象模式也难以准确地描述大气中各种气象要素的相互变化关系，因此难以对其定性和定量计算进行预测。目前，用于研究气象要素的方法分为以下几类：数学模型和机器学习方法。钱悦等人利用基于后向轨迹HYSPLIT模型和潜在源解析PSCF对江西省(赣州市)臭氧污染特征与气象因子的关系进行了分析[7]。尹晓梅等人利用后向轨迹及WRF-CAMx模式针对气象要素及污染物浓度进行了特征分析，得到了供暖结束前后的污染物演变规律[8]。上述是基于现有数学模型的研究方法，在气象要素的分析研究中，机器学习的算法应用得越来越广泛，在预测方面表现出巨大的潜力。随着科学技术的发展，机器学习算法之一的神经网络已成为许多领域进行预测的强大工具。黄建风等人利用小波-NAR神经网络技术，提出气象要素的时间序列预测原理与方法[9]，刘洋等人研究了降雨及其多种相关参数(PWV,温度,相对湿度,露点温度,年积日,日积时)间的时变特征,并构建了基于径向基(radial basis function，RBF)神经网络的短期降雨预测模型[10]。Peng Zhen等人提出一种PS-FCM模型并将其挖掘方法应用于雾霾污染因果挖掘和预测[11]。

基于气象要素的监测数据，采用智能算法进行分析，建立预测模型，已成为新的研究方向之一。然而采用现有数学模型进行分析模拟需要考虑本地化，设置相应的参数化方案。而且WRF都是中尺度模式，对于小尺度的模拟不够精确，所以模拟出来的分辨率还比较粗[12]。而神经网络独有的黑匣子特性，导致无法解释其预测机理，随着模型预测规模的增加，误差也随之增加。

由于气象要素之间彼此制约的特点符合模糊认知图的运行机制，故该文将FCM应用于气象预测领域，提出一种基于FCM的气象要素相关性模型。首先以相邻气象监测点的以时间为序列的数据集作为研究对象，对历史数据通过相关分析法获得影响权重，构建关系矩阵，进而建立气象要素相关性模型进行研究，可对未来的气象要素进行较为准确地推算。

1 模糊认知图

模糊认知图(fuzzy cognitive map，FCM)由节点和加权弧(连接，边)组成，它们以图形形式显示为带可选反馈环的带符号加权图。图上的节点表示描述系统行为特征的概念。概念可以是系统的输入、输出、变量、状态、事件、动作、目标和趋势[13]。带符号的加权弧表示概念之间存在的因果关系。模糊认知图的推理使用一种源于神经网络的方法，可以迭代计算因子对彼此的影响。网络稳定之后，结果显示系统内的趋势。由于模糊认知图允许反馈循环，新激活的概念可能会影响以前已经激活的概念，最后，激活通过非线性的方式通过模糊认知图传播，直到系统达到一个稳定的极限环或者不动点[14]。

图1说明了一个简单的FCM，由六个概念l=1,2,…,6组成。这六个要素作为概念节点集合C,C={C1,C2,C3,C4,C5,C6}，同时也定义了各要素之间的关系权值矩阵W，如公式(1)所示，权重表示概念之间的因果关系。

C1C2C3C4C5C6

(1)

Kosko[15]提出了一规则，根据相互关联的概念的影响来计算每个概念的值，其中下列函数被归一化到区间[-1,1]：

(2)

2 基于模糊认知图的气象要素预测模型

由于气象模式的不确定性和气象要素之间相互影响的特点，将模糊认知图应用到气象背景中，研究气象要素间的关系。

2.1 基于模糊认知图的气象要素相关性模型

利用FCM可以动态地衡量时间序列中概念的前一时刻对后一时刻的影响程度的特性，本节将FCM引入气象要素的相关性建模中，建立一个气象要素相关性模型，将气象要素作为概念，要素之间的相关系数作为加权弧，通过FCM体现要素和要素之间的相关性。

构建的模糊认知图如图2所示。以九个气象要素l=1,2,…,9作为概念节点集合C，C={C1,C2,…,C9}。将节点之间的关系表示为矩阵Wl，如公式(3)所示，节点之间的关系作为有向连线，ωij表示要素和要素之间的相关性，其中ωij为正表示节点之间是正相关，为负则表示节点之间是负相关。ωij根据公式(3)其初始关系权值可以算出。

(3)

2.2 基于相关分析法的关系矩阵初始化

(4)

(5)

(6)

wij是要素i和j之间的相关系数，表示气象要素之间的相关程度，处于[-1,1]之间。wij>0，表示要素对要素有促进作用；wij<0，表示要素对要素有减弱作用；wij的绝对值越接近于1，表示要素i和要素j之间的关系越密切，wij的绝对值越接近于0，表示两要素无关。在该模型中，l=9,即共有9个概念节点，对于气压(P)和露点温度(Td)这两个要素来说，它们之间的相关性可以表示为：

(7)

2.3 基于遗传算法的关系权值的优化

由于模糊认知图属于神经网络的一种，且之前受到专家领域的知识、经验和个人主观性的干扰，使得得出的结果缺乏一定的客观性。鉴于这个缺点，该文采用基于数据驱动的实数编码的遗传算法通过时间序列历史数据构成模糊认知图。

遗传算法包括选择、交叉、变异三个步骤，适应度fitness低的个体会被逐步淘汰，而适应度高的个体会越来越多，经过多代的自然选择后，保存下来的个体都是适应度很高的[13]。err表示适应度函数中预测值和真实值的均方误差。

(8)

(9)

式中，N为模糊认知图中概念节点的个数，即衡量个体的指标数，L为模糊认知图中每个概念节点的原始数据的个数，即个体的个数。

利用模糊认知图对时间序列数据进行预测，该文采用一步领先预测的方法，即根据上一时刻的数据对下一时刻的数据进行预测的方法。即根据T-1时刻的数据预测T时刻的数据。

(10)

f(·)表示激活函数，数据进行完一次迭代以后通过激活函数，其输出值即为预测值。激活函数可以将非线性因素引入到模糊认知图的计算当中，使得模糊认知图可以逼近非线性函数，这样模糊认知图可以应用到众多的非线性模型中。模糊认知图的结构源于神经网络，因此激活函数也与神经网络的激活函数一脉同源，在此采用Tanh函数作为激活函数。

(11)

构建模糊认知图之前，先将数据集分为两部分。将一年中每个季节的70%数据作为训练集，将剩下的每个季节的数据作为测试集。

关系权值的优化流程如下：

(1)编码：将九个要素对自身的关系权值设置为1，要素的关系矩阵对应81个权值。需要将位于1和-1之间的81个权值进行实数编码，W在遗传算法中称作染色体，Wj= {w11,w12,…,w99}。

(2)初始化种群：构建过程中已经通过历史数据使用相关分析法确定了j个适应值较大的染色体Wj(j=1,2,3,4)作为初始种群。

(3)适应度计算：按照公式(8)计算种群中每条染色体的适应度。

(4)选择：通过处理历史数据得到了最优染色体，此步骤将精简得出的每条染色体保留并参与交叉和变异操作，直接插入到新种群pop中。

(5)交叉：实验中设置交叉率参数Pc。该步骤的操作对象是实数数串Wj，任选数串中的一个数据位置作为交叉点。例如染色体W1，若选中染色体中第三个元素w13作为交叉点，则这条染色体第三个元素与其之后的第九个元素相互交换，构成新的一条染色体参与下一步的变异操作。每次交叉之前，生成一个0到1的随机数，若该随机数大于Pc则进行本步操作，否则不进行。

(6)变异：设置变异率参数Pt，在变异之前产生一个0到1的随机数，如果该随机数大于Pt，则进行变异，否则不变异，变异时随机产生染色体中的位置，其值按照公式(12)进行修改，其中r为0到1之间的任意浮点数，MaxPerturbation为最大变异步长[14]。

(7)迭代：重复执行第3到第6步，将变异后的新染色体插入到种群pop中，直到达到种群上限或者适应度基本不变为止。

w=w+(r-1.0)×MaxPerturbation

(12)

关系权值优化的伪代码如下：

算法1：用实数编码遗传算法构建模糊认知图。

输入：训练集，初始化的权值矩阵,交叉概率Pc，变异概率Mt，最大迭代代数T，最大变异步长MaxPerturbation

输出：最佳权值矩阵。

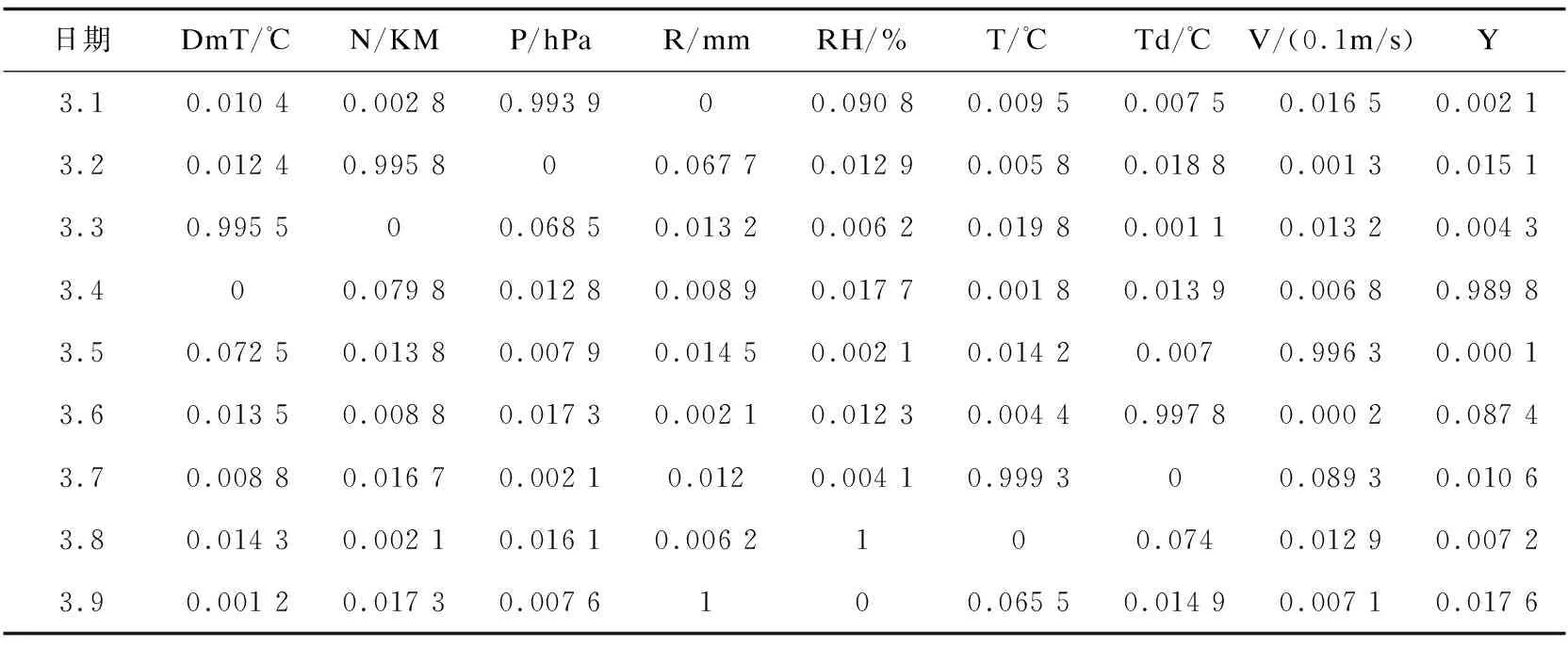
1. while i

2.保存该种群中染色体的适应度

3.将此染色体插入下一代种群popj

4. while n

5.对此个体按交叉概率Pc执行交叉操作

6.对此个体按变异概率Mt执行变异操作

7.这个新染色体插入下一代种群popj

8. end while

9. i++

10. end while

通过上述步骤构建出了基于模糊认知图的气象要素相关性模型，首先应用相关分析法将关系矩阵初始化，然后对初始化后的权值矩阵通过遗传算法进行优化。

3 实例与实验分析

3.1 数据的收集与处理

实验选取的是某市2018年末和2019年两个气象监测站点共24个点位的监测数据，观测了逐日逐时的地表温度(Dmt)、能见度(N)、本站气压(P)、降水量(R)、相对湿度(RH)、温度(T)、露点温度(Td)、风速(V)和云量(Y)九个气象要素数据。根据气温的起伏变化将实验数据分为四季，2018年12月到来年2月为冬季，3月到5月为春季，6月到8月为夏季，9月到11月为秋季。通过相关性分析与合并处理，最终得到乐山市一年中四个季节不同气象要素的相关系数。表1为3月份的部分数据。

表1 春季的部分气象数据

由上述表1和图3可知，各个要素的取值范围存在较大差距，因此在使用数据的时候需将数据进行预处理。

数据预处理包括两个步骤：

(1)除了降水量R这一指标外，对每个因素每天的24个点位的数据取平均值，对降水量R的24个数据求和，其结果作为当日的数据结果。

(2)由于站点数据的差异较大，因此对参与模型构建的数据进行标准化处理，将上一步处理好的数据压缩到0和1之间，这里采用公式(13)最大最小值法标准化数据结果。

(13)

以平均值为代表的春季的数据值归一化后的部分如表2所示。

表2 春季数据的归一化值

3.2 关系矩阵的构建

FCM中的权重矩阵可以用来分析因果关系和推断预测结果。首先运用气象学中常用的相关分析法初始化权重矩阵。图4为春季的初始化权重矩阵。

由于利用相关分析法得到的关系矩阵的适应度还存在改进的空间，利用公式(8)～公式(12)对矩阵不断交叉变异，在迭代10 000次优化之后，将最大适应值的权重矩阵保存下来。经过实验发现不同的变异步长，得到的实验结果不尽相同，下面列举了五个不同的步长所产生的不同的适应值。图5为适应值随变异步长r的变化趋势。