基于特征选择和优化极限学习机的短期电力负荷预测

2022-04-02商立群李洪波侯亚东黄辰浩张建涛

西安交通大学学报 2022年4期

商立群,李洪波,侯亚东,黄辰浩,张建涛

(西安科技大学电气与控制工程学院,710054,西安)

电力负荷预测作为电网规划中的重要组成部分,对于电力系统安全经济运行具有重大意义。精确的电力负荷预测,特别是短期电力负荷预测,既能保障人们用电可靠和电网安全稳定运行,也能使电力行业的效益极大地提升[1-2]。

早期的电力负荷预测方法是基于数学统计理论中的模型提出的,如趋势外推法、时间序列法、回归分析法、灰色系统法等传统预测方法[3-4]。由于这些预测方法的模型单一,且对于时间序列的平稳性要求较高,使得预测的结果误差大、精度低[5],随着人工智能技术的发展,机器学习及人工智能等方面的算法被广泛应用于电力负荷预测领域,如专家系统、支持向量回归、人工神经网络等[6-9]。专家系统缺乏自主学习能力,负荷预测精度会受其对突发性事件和不断变化的条件适应性较差的影响[10-11]。支持向量回归采用结构风险最小化原则解决小样本数据,预测效果较好,但其核函数参数的选取限制了最终的预测精度[12-13]。人工神经网络相对复杂,它要通过反向传播以调整网络权值和阈值,收敛速度慢,需要消耗大量的训练时间才能得到较为准确的预测结果[14-15]。极限学习机(ELM)的提出很大程度上弥补了传统的人工神经网络的缺点,在学习速率和泛化能力方面具有较大的优势,只需随机产生输入层与隐含层之间的权值以及隐含层的阈值并训练对电力负荷进行预测,但利用随机数作为初始参数会导致ELM的稳定性下降[16]。准确选择合适的特征对于短期电力负荷预测尤为关键,而短期电力负荷原始时间序列的历史负荷特征及外部影响因素多样而复杂,仅依靠机器学习进行预测很难达到更高的精度,因此对原始数据进行优选和降维十分重要。

针对负荷预测的特征选择问题,文献[17]利用核主成分分析法对外部气象因素进行优选,但并未对历史负荷特征进行最优选择。文献[18]利用最大互信息系数对历史负荷特征及外部影响因素进行筛选,取得了较好的结果,但筛选后的特征中仍具有较大的信息冗余,且未对最优特征维数进行确定和检验。针对ELM模型在预测时产生的稳定性问题:文献[19]利用蝙蝠算法对ELM的隐含层节点数进行优化,但并未对权值和阈值进行优化;文献[20]利用改进遗传算法对ELM的权值和阈值进行优化,一定程度上提高了ELM的稳定性,但算法过程较为烦琐;文献[21]利用多目标粒子群算法优化ELM的参数权值和阈值,但单一的粒子群算法存在易陷入局部最优解而导致参数优化不佳的缺点,会对ELM的稳定性产生不良影响。

针对这些问题,本文提出基于格拉姆-施密特正交化与皮尔逊相关性分析相结合特征选择方法(GSO-PCA)和改进灰狼算法(IGWO)优化极限学习机的短期电力负荷预测模型(IGWO-ELM)。分别使用GSO和PCA对两种不同类型特征进行优选,并根据平均绝对百分比误差(MAPE)确定最优特征集,这样既可保留大量的负荷原始数据信息,也可避免负荷信息的重叠,与常见的特征选择方法比较,验证了其优越性;将Tent混沌映射和粒子群算法(PSO)融入到灰狼算法中,得到IGWO算法,并使用两种典型的测试函数验证了IGWO算法具有更强的寻优能力;利用IGWO算法对ELM的参数进行动态优化,建立IGWO-ELM短期负荷预测模型;将同一最优特征集分别输入到ELM、GA-ELM、PSO-ELM、GWO-ELM和IGWO-ELM模型中进行短期电力负荷预测,并对所得结果进行比较与分析。实例分析验证了本文所提的负荷预测模型具有更高的预测精度和更强的泛化能力。

1 GSO-PCA特征选择方法

电力负荷具有显著的特性和变化规律,但一些外部因素会对它产生重大影响,如气象、日期类型等,因此要精确预测未来的负荷变化情况必须充分考虑负荷自身的变化规律以及相关影响因素[22]。本文将负荷预测特征分为两大类:反映负荷自身变化规律的特征(预测时刻之前的负荷值)与外部影响因素特征(气象、日期类型等)。本文分别使用GSO算法和PCA对两种不同类型特征进行优选,并根据MAPE确定最优特征集。在保证预测精度的前提下,既提取了表达负荷的有效信息,避免了冗余信息的出现,也弥补了经验特征选择方法标准缺乏的不足。

1.1 GSO算法原理

GSO算法是一种前向选择方法,可根据研究目标之间的正交性对特征进行筛选并排序[23]。为了选择与输出量相关的最佳特征,计算每个特征xk与其输入量y的余弦值作为评价指标,表达式为

(1)

式中:xk=[xk1,xk2,…,xkm]T,xkm为第m个样本的第k个特征量;y=[y1,y2,…,ym]T为输出量;φk为第k个特征量与输出量y之间的夹角;〈xk,y〉为xk和y之间的内积。cosφk越接近1,则输入特征与输出量越相关;反之,则越不相关。因此,在筛选过程中,选择评价指标大的特征作为目标的最相关特征,本文将满足cosφk≥0.7的负荷特征作为最相关特征。与经验特征选择方法进行负荷特征选择相比,GSO算法选择的负荷特征更能体现负荷的变化规律,避免了负荷信息冗余的出现。

基于GSO算法的负荷特征选择方法步骤如下。

步骤1将历史负荷时间序列分为训练集和测试集,根据测试集中的样本确定各预测时刻的真实负荷值。

步骤2将数据归一化后,构造每个预测日的特征量矩阵和输出量矩阵;特征量矩阵由各历史负荷特征组成,输出量矩阵由预测日各时刻负荷值组成。

步骤3根据相关条件对各历史负荷特征进行筛选并排序,获得最相关负荷特征。

基于GSO算法的负荷特征选择流程见图1。

图1 基于GSO算法的负荷特征选择流程Fig.1 The process of load feature selection based on GSO algorithm

1.2 PCA原理

电力负荷预测除了与自身的变化规律相关,与外部影响因素也密不可分。PCA是一种被广泛用来描述变量相关性的方法,其核心思想是通过皮尔逊相关系数(PCC)来反映变量的相关程度。

设Xi={xi(1),xi(2),…,xi(k),…,xi(n)}为外部影响因素集合,i代表第i个影响因素,k代表第k天,Yj={yj(1),yj(2),…,yj(k),…,yj(n)}为负荷集合,j代表第j个负荷类型,则Xi与Yj之间的皮尔逊相关系数表达式为

(2)

皮尔逊相关系数rX,Y取值范围为[-1,1],|rX,Y|越大,则X与Y之间的相关度越强。具体相关程度关系如表1所示。本文选择皮尔逊相关系数大于等于0.4的影响因素构建特征集。

表1 皮尔逊相关系数相关程度关系Table 1 Related degree relationship table of Pearson correlation coefficient

1.3 GSO-PCA特征选择工作流程

基于GSO-PCA的特征选择流程如图2所示。

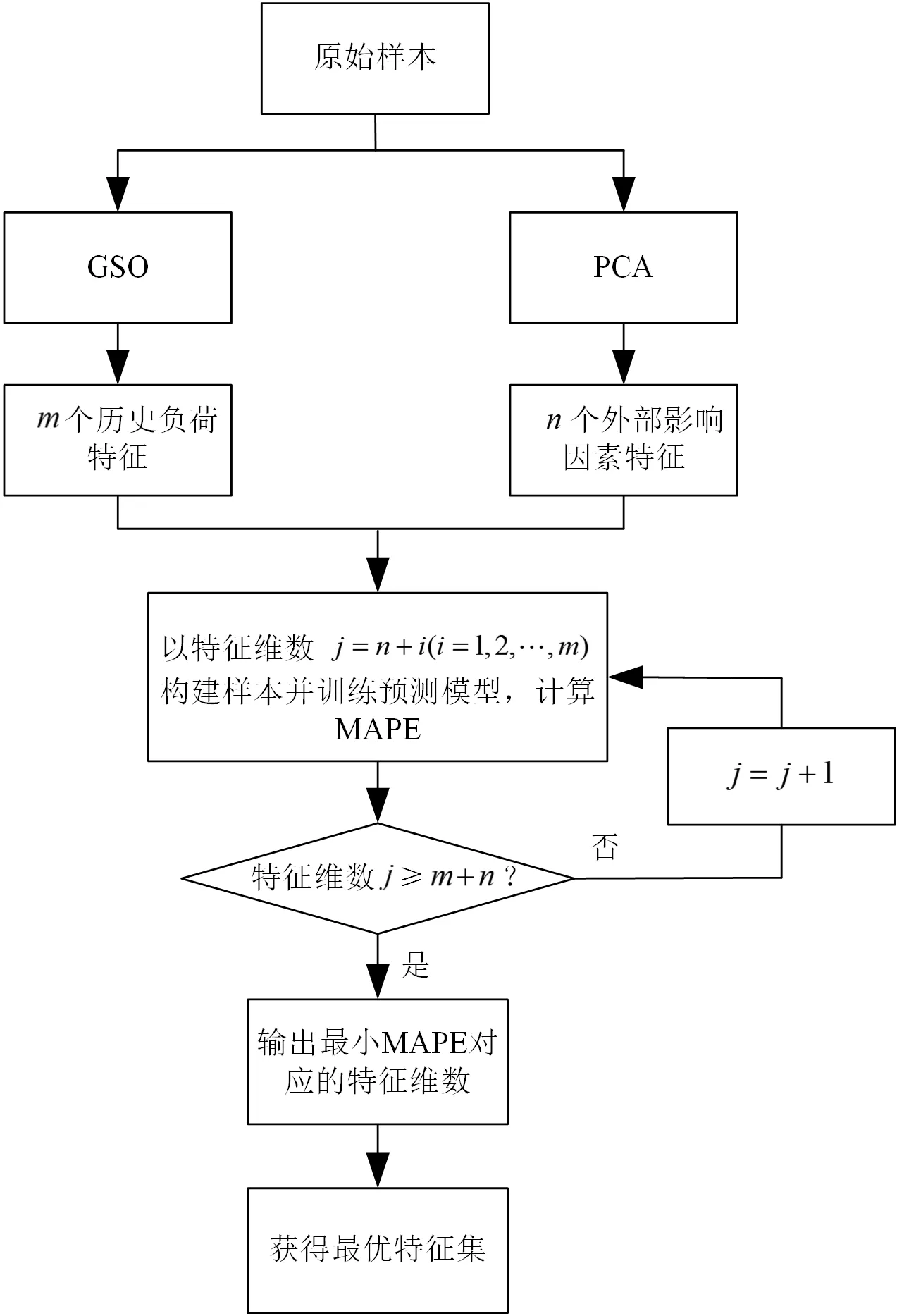
图2 基于GSO-PCA特征选择流程Fig.2 The process of feature selection based on the GSO-PCA

2 极限学习机原理

极限学习机是一种基于前馈神经网络构建的机器学习方法。ELM的基本原理是随机生成输入层与隐含层之间连接的权值以及隐含层节点的阈值,并设置隐含层神经元数,然后经过简单的矩阵计算便可获得唯一最优解的过程。与传统的前馈神经网络算法相比,ELM具有学习速率快、泛化性能强等优点,它不仅能解决回归、拟合等问题,还在分类、模式识别等领域得到了广泛的应用。

极限学习机的数学模型为

(3)

式中:ωi=[ωi1,ωi2,…,ωim]为输入权值矩阵;βi=[βi1,βi2,…,βin]T为隐含层输出权值矩阵;tj=[tj1,tj2,…,tjn]T为网络输出矩阵。式(3)通过一系列的推导可得

Hβ=T

(4)

ELM的学习过程相当于一个非线性优化问题。当激活函数无限可微时,ELM可以随机选择输入权值和隐含层的阈值,且隐含层的输出矩阵在训练过程中保持不变。此时,ELM的学习过程可等价求最小二乘解,其解可表示为

β*=H+T

(5)

式中H+为隐含层输出矩阵H的Moore-Penrose广义逆。

3 灰狼算法及其改进

3.1 基本灰狼算法

灰狼优化(GWO)算法[24]是一种新型的群智能优化算法,其灵感来源于自然界中灰狼种群的严格社会等级制度和捕食行为。自然界中的灰狼种群分为4个等级,从高到低依次为α狼、β狼、δ狼、ω狼。α狼、β狼、δ狼为灰狼领导层,且数量仅为一只,对狼群的狩猎起领导和决策作用,其余均为ω狼,配合灰狼领导层搜索猎物的工作。算法核心是利用ω狼在搜索猎物过程中的不同位置,与上层狼群位置进行比较,将更优的位置赋予上层狼群,最终达到寻优的目的。设灰狼种群中有N头狼,在d维空间内搜索,则第i头灰狼在的位置为xi=[xi,1,xi,2,…,xi,d]T。基本灰狼算法描述如下。

(1)猎物位置确定。在狩猎的过程中,猎物所在的位置更接近灰狼领导层,因此ω狼可根据灰狼领导层的位置确定猎物的位置,表达式为

(6)

式中:Xα(t)、Xβ(t)、Xδ(t)分别为灰狼领导层α狼、β狼、δ狼的位置向量;Dα、Dβ、Dδ分别为ω狼与灰狼领导层α狼、β狼、δ狼之间的距离向量;X(t)为当前ω狼的位置向量;C1、C2、C3均为系数向量,分别代表ω狼与灰狼领导层α狼、β狼、δ狼之间的搜寻距离权值;r2为区间[0,1]的随机向量。

(2)灰狼位置更新。当灰狼领导层α狼、β狼、δ狼的位置确定后,需要对领导层周围的猎物进行围捕,表达式为

(7)

式中:X(t+1)为ω狼更新后的位置向量;A1、A2、A3均为系数向量,分别代表ω狼与灰狼领导层α狼、β狼、δ狼之间的位置距离权值;r1为区间[0,1]的随机向量;Tmax为最大迭代次数。

当猎物停止移动时,灰狼种群会对猎物进行攻击,即寻得最优值。a、A、C在相应区间内发生变化时,每迭代一次,灰狼种群个体就会更新位置,直至接近并寻得猎物(最优值)。

3.2 改进灰狼算法

3.2.1 Tent混沌映射

Tent映射是一种分段混沌映射函数,其数学表达式为

(8)

式中a为[0,1]的常数。若Xn+1>1,则Xn+1返回值为1;若Xn+1<0,则Xn+1返回值为0。

由于基本灰狼算法是采用随机初始化的方法来确定种群初始位置的,导致灰狼个体在初始解空间内分布不均,极大地影响了灰狼算法的整体求解性能。混沌序列时常被运用于优化搜索问题,研究表明,Tent混沌映射得到的序列在随机性、均匀性、遍历性等方面相比于其他混沌映射具有较大的优势[25]。因此,本文采用Tent混沌映射产生的序列对灰狼种群初始化,有利于使初始的种群位置在初始解空间内分布更加均匀、范围更广。

3.2.2 粒子群优化算法

粒子群优化算法是一种传统的智能优化算法,其原理是空间中的粒子群通过不断迭代,跟踪个体最优值和全局最优值这两个极值,以更新自己的位置和速度,直至寻得满足终止条件的最优值。更新位置和速度表达式为

(9)

灰狼算法本身具有一定的位置优化能力,但其在寻优过程中缺少群体位置与个体位置的交流,因此易陷入局部最优解。PSO算法具有易实现、收敛速度快且对控制参数具有较强的鲁棒性等优点。因此,将粒子群优化算法融合到灰狼算法中,通过粒子群的位置更新来代替灰狼种群最终的位置更新,使得灰狼种群在寻优过程中具有更好的记忆能力,并在灰狼位置更新时加入ω惯性因子,以提高灰狼算法的局部搜索能力。由此,式(6)转化为

(10)

式中θ为[0,1]内的随机数。式(9)可转化为

(11)

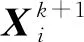
改进灰狼优化算法流程如图3所示。

图3 IGWO算法流程Fig.3 The process of IGWO algorithm

3.3 IGWO算法性能测试

为了测试IGWO算法的性能,本文采用两种典型的单峰和多峰测试函数,并与PSO算法和基本的GWO算法进行对比。测试函数表达式为

(12)

(13)

不同测试函数的取值范围、最优解等信息如表2所示,不同算法的参数设置如表3所示。

表2 测试函数信息而最优值和标准Table 2 Information of test function

表3 不同算法的参数设置Table 3 Parameter settings of different algorithms

将算法的最大迭代数Tmax设置为1 000,种群规模N设置为30。对于测试函数,在迭代数一定时,平均值可以反映算法的寻优精度,方差可以反映算法的稳定性和鲁棒性。为避免单次运行结果所带来的偏差,本实验分别对2个测试函数独立运行30次,得到各测试函数的最优值、平均值以及标准方差。测试函数优化结果比较见表4。

表4 不同测试函数优化结果对比Table 4 Comparison of optimization results of different test functions

由表4可知,IGWO算法优化得到的最优值更接近真实最优解,且平均值和标准方差小于PSO算法和GWO算法优化的结果。相较于PSO算法和基本的GWO算法,IGWO算法具有更好的稳定性和寻优能力,能更快速而准确地得到最优解。

4 IGWO-ELM短期电力负荷预测模型

在传统的ELM中,输入层与隐含层之间连接的权值以及隐含层节点的阈值是随机生成的,这大大节省了ELM的训练时间,但也不可避免地会出现产生的随机值并非最优的情况。这一方面使ELM相较于其他人工神经网络需要更多的隐含层神经元,另一方面使得到的隐含层输出矩阵出现较大偏差,进而使ELM的泛化能力大大减弱,输出也极不稳定。因此,对ELM的权值和阈值进行优化十分必要。

本文采用IGWO算法对ELM参数进行优化,利用IGWO算法的全局及局部寻优能力,找出最优的权值和阈值参数。将优化后的参数代入到ELM中对短期电力负荷进行预测。IGWO-ELM预测模型建立步骤如下。

步骤1参数初始化。设置灰狼种群数量N、种群维度D、最大迭代数Tmax。

步骤2初始化灰狼种群。使用式(8)对灰狼种群初始化。

步骤3计算参数a、A、C,将所有权值和阈值的组合作为每个灰狼个体的位置,并计算每一匹狼的适应度。本文将训练集中实际值和预测值之间的均方根误差作为适应度函数,适应度排名前3的分别作为α狼、β狼、δ,其余均为ω狼。

步骤4利用式(10)更新灰狼种群个体的位置,并更新参数a、A、C。

步骤5引入粒子群优化算法,更新灰狼种群个体的位置。利用式(11)对灰狼种群个体位置进行更新。

步骤6计算灰狼新位置的适应度,并与上一次迭代的适应度比较。若适应度优于上一代,则更新,否则不变。

步骤7判断是否已达到最大迭代数。若是则结束,并输出最优权值和阈值的组合,否则跳转至步骤3。

步骤8利用优化后的ELM模型对短期电力负荷进行预测,并对结果进行分析。

基于IGWO-ELM的短期电力负荷预测流程如图4所示。

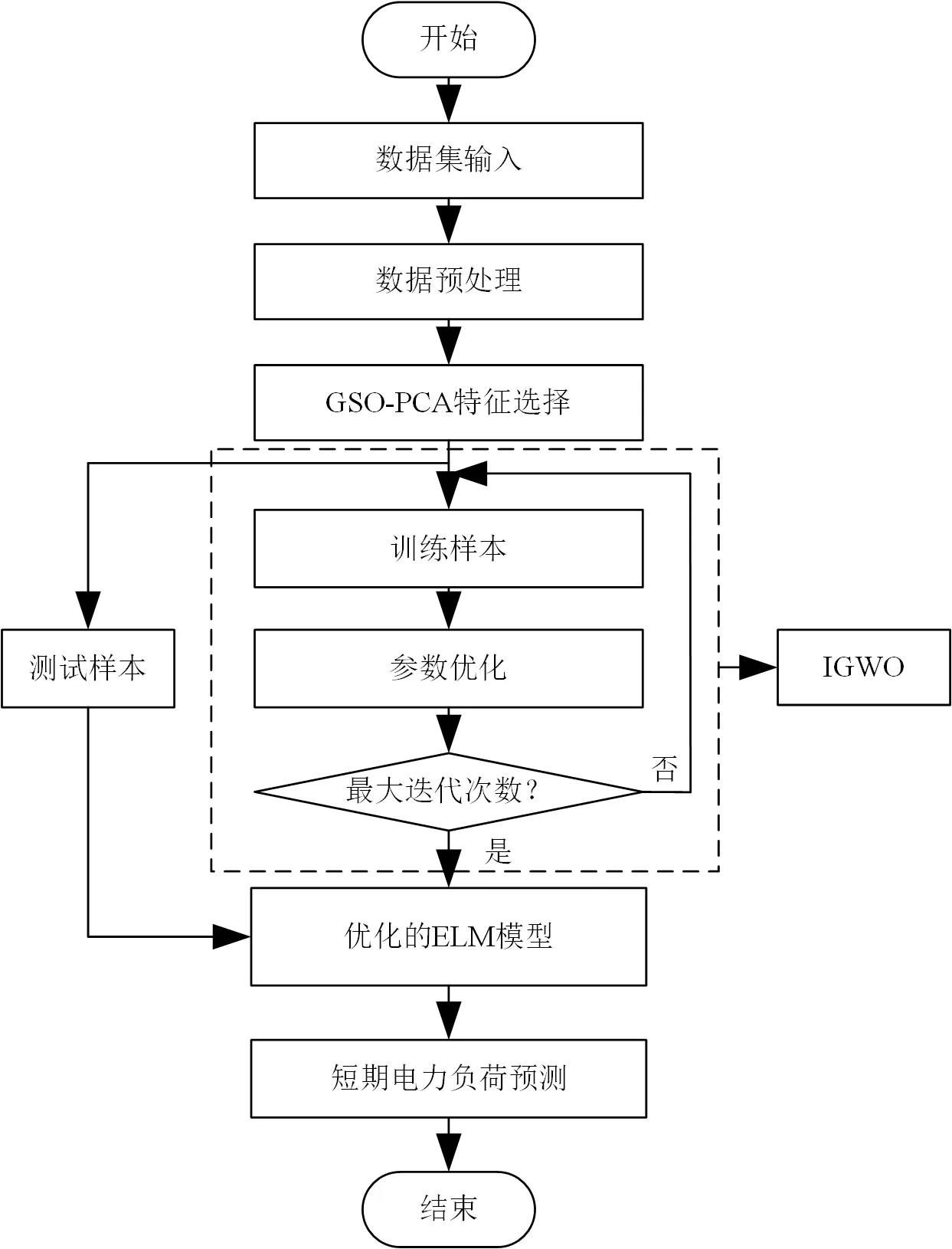
图4 基于IGWO-ELM的短期电力负荷预测流程Fig.4 The process of short-term power load forecasting based on IGWO-ELM

5 实例分析及仿真实验对比

本文采用第九届电工杯数学建模提供的实例数据集,从中选取2014年1月1日至2014年12月31日的电力负荷及气象数据,采样周期为15 min,数据集共有35 040条负荷数据。选择常用的负荷预测评价指标,将本文IGWO-ELM预测模型与传统ELM、GA-ELM、PSO-ELM以及GWO-ELM预测模型进行对比分析,验证本文模型的有效性和优越性。

5.1 数据归一化及评价指标

为避免因变量间的数量级不同而产生误差,对数据进行预处理,将数据统一归一化至[0,1]。

为了更好地评估不同负荷预测模型的精度,本文选用4种常用的负荷预测评价指标,即拟合优度检验系数R2、平均绝对误差、均方根误差和平均绝对百分比误差,表达式分别为

(14)

(15)

(16)

(17)

5.2 GSO-PCA特征选择

利用GSO算法优选出最相关负荷特征。基于现有相关文献研究[26-28],构建原始负荷特征集,共37个,其中包括预测时刻前几个小时的负荷值、前几日或前几周同一时刻的负荷值。具体历史负荷特征如表5所示。本文研究短期电力负荷预测,故以预测日为1天的特征选择为例。首先将样本数据进行归一化处理,然后利用GSO算法筛选出最相关的负荷特征,结果表6。

表5 历史负荷特征Table 5 Historical load features

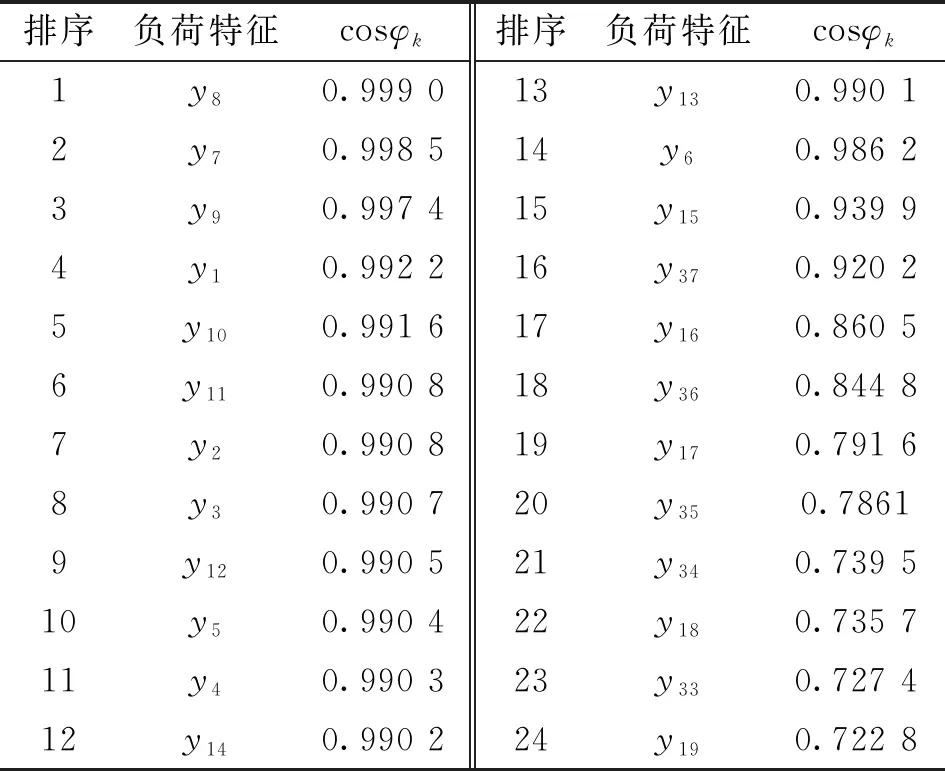
表6 GSO算法优选的最相关负荷特征Table 6 The most relevant load features preferred by the GSO algorithm

由表6可知,GSO算法筛选后所得各负荷特征的评价指标cosφk均在0.7以上,说明优选得到的负荷特征与预测时刻负荷高度相关。对各负荷特征的评价指标进行排序,排序越靠前,则表示该负荷特征与预测时刻负荷相关度越强,为后文最优特征集确定作准备。

对于外部影响因素采用皮尔逊相关性分析方法。原始数据中包含日最高温度x1、日最低温度x2、日平均温度x3、相对湿度x4和降雨量x5,考虑日期类型x6对不同负荷类型的影响,按照工作日记为1、双休日或法定节假日记为0的原则统计数据。根据表1,利用皮尔逊相关性分析剔除低相关的影响因素。不同负荷与单一影响因素的皮尔逊相关性分析如表7所示。由表7可知,日最高温度、日最低温度、日平均温度与负荷之间的皮尔逊相关系数r均超过0.6,表明为强程度相关,且显著检验均为显著。日期类型与日最小负荷之间的r只有0.2,但与日最大负荷和日平均负荷之间的r均超过0.4,因此将日期类型与负荷视为中等程度相关。相对湿度和降雨量与负荷之间的r较小,且显著检验均为不显著,由此说明在此数据集下,相对湿度和日降雨量与负荷的相关度不强,对负荷的影响几乎可以忽略,故外部影响因素最终选择日最高温度、日最低温度、日平均温度和日期类型。

表7 不同负荷类型与单一影响因素的皮尔逊相关性分析Table 7 Pearson correlation analysis of different loads and single meteorological factor

为了确定最优特征集Zm,将4个相关度最强的外部影响因素和负荷特征组合的特征集分别输入到ELM模型中,采用交叉验证法,并根据MAPE确定最优特征集。eMAPE越小,则代表该特征集对应的负荷预测精度越高。仿真结果显示,当特征维数少于7时,eMAPE会超过1,由此表明选择合适特征维数对于预测十分关键。当特征维数大于等于7时,特征维数与MAPE的关系如图5所示。由图5可知:当特征维数m为20时,eMAPE最小;当特征维数m大于20时,eMAPE反而有所增加。由此说明特征维数为20时ELM模型预测效果能达到最佳,后加入的特征会给预测效果带来不利影响,因此将20个特征组成的最优特征集Zm作为ELM的输入。

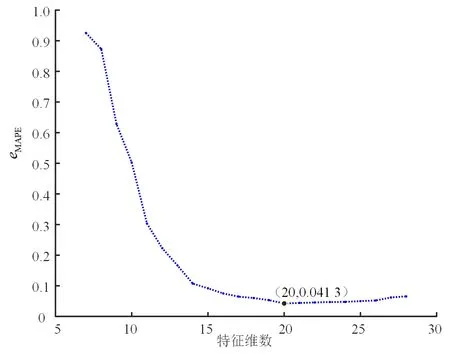
图5 特征维数与MAPE的关系Fig.5 The relationship of feature dimension and MAPE

经GSO-PCA特征选择后的最优特征集见表8。为验证GSO-PCA特征选择方法的优越性,与以往的特征选择方法进行对比,分别计算MAPE。

表8 最优特征集ZmTable 8 The best feature set Zm

以往的特征选择方法主要分为经验特征选择法和机器学习特征选择法两类。在对比实验中:对于经验特征选择法,直接选用温度、预测日前1～7天同一时刻的负荷值作为最优特征集;对于机器学习特征选择法,选用最大互信息系数(MIC)和随机森林(RF)[29]对特征进行优选。具体对比数据见表9。

表9 不同特征选择方法的误差对比Table 9 Error comparison of different feature selection methods

由表9可知,本文提出的特征选择方法优于其他两类方法。与经验特征选择方法相比,能够较好地筛选出与预测时刻相关度高的特征;与单一的机器学习特征选择方法相比,能够更好地解决数据样本信息冗余、特征维数难以确定等问题。

5.3 实例分析与仿真实验对比

为了验证IGWO-ELM模型的优越性,本文在保证相同最优特征集条件下,选择不同算法优化的ELM模型进行对比实验,具体步骤如下。

步骤1确定训练集和测试集。将2014年3月1日—2014年3月14日两周的负荷数据作为训练集,共1 344个样本。将2014年3月15日至3月17日3天的数据作为预测集,共288个样本。

步骤2确定输入量和输出量。利用GSO-PCA特征选择方法分别确定3个预测日的最优特征集,并以此为基础分别构建训练集和测试集,每个样本包括输入量和输出量,输入量由最优特征集组成,输出量为各个预测时刻的的负荷值。

步骤3对数据进行预处理。将样本数据统一归一化至[0,1]。

步骤4设置ELM模型相关参数。以MAPE为评价指标,通过多次仿真可知,当隐含层节点数为125时MAPE最小,因此ELM隐含层节点数设置为125,激活函数设置为Sigmoid函数。

步骤5得出结果并分析。将预处理后的样本数据分别输入不同的预测模型,得到预测结果并对结果进行误差分析。

本文的仿真实验平台为Windows 10操作系统、内存16 GB的计算机,运行环境为Matlab软件。为了保证所得结果的有效性和可靠性,算法的种群数量均取30,最大迭代数均取200。不同算法参数设置如下:GA算法的交叉概率pc为0.7,变异概率pm为0.3;其余算法参数设置与3.3小节一致。

为了避免单次运行结果产生偏差,分别对不同预测模型独立运行4次,即5种预测模型共运行20次。对每种预测模型得到的4种负荷预测结果求和并取均值,得到各个不同预测模型的预测结果以及评价指标。表10为不同模型的预测精度对比,图6为不同模型的预测结果对比。

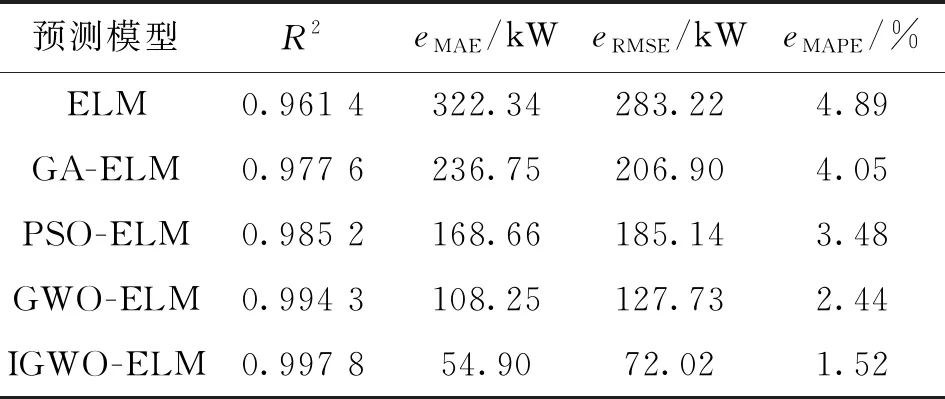
表10 不同负荷预测模型精度对比Table 10 Comparison of accuracy of different load forecasting model

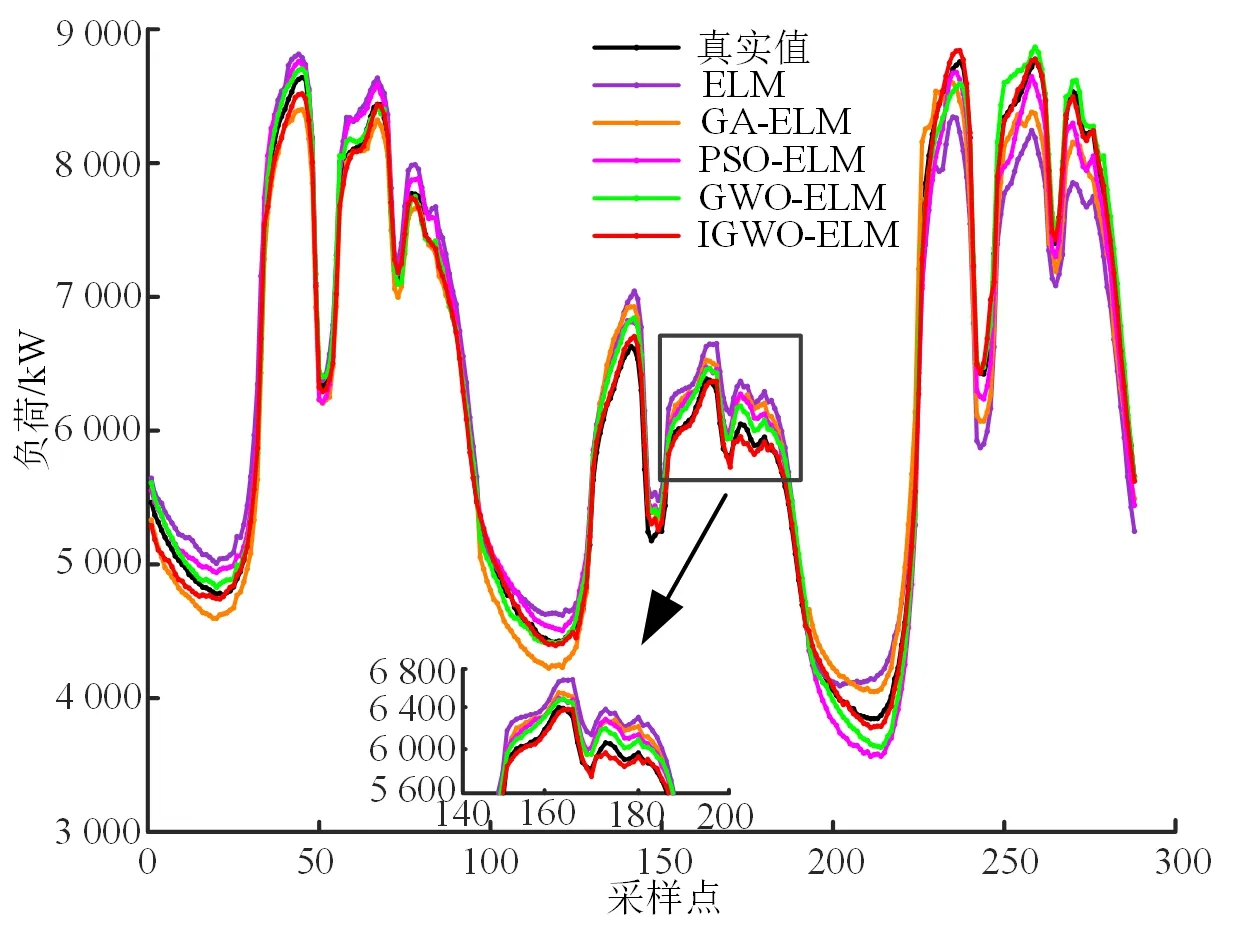
图6 不同负荷预测模型预测结果对比Fig.6 Comparison of results of different load forecasting model

由图6的局部放大图可知,本文预测模型所得的结果与真实值更加吻合。由表10可知:从拟合优度检验系数R2分析,本文所提预测模型的R2最接近1,拟合效果最好;从平均绝对误差分析,本文所提预测模型与ELM、GA-ELM、PSO-ELM以及GWO-ELM预测模型相比,eMAE分别下降了267.44、181.85、113.76和53.35 kW;从均方根误差分析,本文所提预测模型与其他传统预测模型相比,eRMSE分别下降了211.2、134.88、113.12和55.71 kW;从平均绝对百分比误差分析,本文所提预测模型与其他传统预测模型相比,eMAPE分别下降了3.37%、2.53%、1.96%和0.92%。综合可知,本文提出的IGWO算法优化ELM的预测模型具有更好的稳定性,负荷预测精度也有明显的提高。