金属矿尾砂浆压缩与剪切屈服应力的关系

2022-04-02焦华喆杨文博杨柳华陈峰宾王金星张文祥

重庆大学学报 2022年3期

焦华喆,杨文博,杨柳华,陈峰宾,王金星,张文祥,苏芮

(河南理工大学土木工程学院,河南焦作 454150)

在中国国民经济构成中,金属矿产资源为各行各业提供基础生产材料,占有及其重要的地位。矿床开采将地下资源转移到地表,不仅产生了大量的固体废物,而且由此产生的井下采空区和地表尾矿库也成为了金属矿山的两个重大危险源[1]。

膏体填充法是将沉积在地表的固体废物变成膏体,回填到井下用来治理采空区塌陷问题,不仅提高了地下采矿作业的安全性,而且充分利用了地表废物,实现了“一废治两害”的目标。目前膏体流变学的研究是矿业浆体流变学的热点和难点。膏体技术包括脱水、搅拌、输送、堆存4个阶段,均涉及到非牛顿流体流变特性。在脱水阶段,全尾砂浆的压缩屈服应力和剪切屈服应力共同影响脱水效果[2]。全尾砂重力浓密脱水工艺中,床层压缩过程是指沉降至容器底部的絮团进一步密实排水的过程[3]。

目前已有的研究进展表明:全尾砂浆重力浓密性能由沉降絮凝和床层压缩两个方面组成[4]。絮凝沉降指的是由于固液密度差,固体颗粒在重力作用下向下沉降,从而在容器上部澄清层。絮凝沉降速度影响最大的是固液分离的效率[5]。床层压缩过程是指沉降至容器底部的絮团进一步密实排水的过程[6]。絮团沉降至容器底部时,在自然状态下进行堆积,堆积面积逐步升高形成床层。由于絮团堆积的不均匀性,造成床层孔隙率大,随着床层高度的升高,在重力作用下,床层下部絮团所受的重力作用大于床层上部絮团,因此,床层内部浓度是不均衡的,其浓度梯度导致床层上下部的渗透性不同,床层的渗透性又影响了浓度的进一步分布。在膏体输送过程中,其关键问题是阻力特性,以往的研究大多注重与从固液两相流的角度出发,考虑颗粒的沉降速度及对流扩散等因素[7]。然而对于膏体来说,由于浆料中存在细颗粒的絮凝作用,因此在其内部有着一定强度的絮网结构,进而导致浆料流动特性的单一性变化,即由两相流呈现为结构流体[8]。研究颗粒的物理与化学特性与其流变特性之间的内在关系,进而研究颗粒在管道中的输送方式,将为进一步研究管道阻力提供基础[9]。压缩屈服应力的改变表征了浆体浓度的变化[10],而在剪切屈服应力的研究过程中浆体的浓度是不发生变化的。目前的研究往往忽略了该特性,也是压缩屈服应力与剪切屈服应力最大的不同。压缩流变特性决定了能够达到的最大脱水浓度,剪切流变特性是影响耙架旋转和膏体底流排放的重要因素[11]。同时浓度与流动性能相互影响,对立统一。但是目前关于压缩流变特性和剪切流变特性关系的研究几乎没有。

笔者从压缩屈服应力和剪切屈服应力两个方面出发,对床层压缩主要的力学过程进行了力学分析和数学建模。并结合其物理意义,发展了全尾砂可浓密性能的表征方法,利用压缩屈服应力和剪切屈服应力2个关键参数来表征全尾砂浆的浆体输送性能和床层脱水阻力,以便对沉降和压缩的统一表征。最终得出了结论:絮团网状结构的压缩屈服应力要远大于其剪切屈服应力,因此剪切作用能够更容易的破坏絮团结构,是脱水的主要外力部动力,从而解释了搅拌脱水的力学机理。

1 全尾砂浆的微观结构特性

在全尾砂可浓密性能表征研究中,絮团特征参数中最重要的是絮团结构的尺寸大小,絮团尺寸大小的变化伴随着絮团结构的变化。因此絮团尺寸影响沉降速度、絮团形状结构的强度影响底流浓度,全尾砂絮团的微观结构和力学行为是影响浓密效果的根本原因。

如图1所示,高浓度床层的微观结构是含有大量水的多孔网状结构,这种网状结构的存在影响了脱水速度和脱水浓度[12]:

图1 未剪切絮团网状结构Fig.1 Mesh structure of unsheared flocs

1)为了提高浓度,需要扰动网状结构,以便排除水分[13];所以网状结构的强度是决定脱水浓度的关键参数;

2)颗粒间距的减小,脱水速度下降,因此浓度开始上升,该浓度下的达西渗透阻力增加[14];因此,网状结构的渗透能力是影响脱水速度的关键参数。

1.1 压缩屈服应力

在絮凝剂的作用下,稳定的悬浮液中颗粒会与其他颗粒连结在一起,形成一个颗粒絮团聚合体结构[15]。当浓度达到一定高度时,就会形成一个渗透到整个悬浮液中的颗粒网状结构。此时,该网状结构具有固体的结构和性质。作用在颗粒上的压缩应力便可在整个网状结构的内部传递。在网状结构中引入固体压力的概念,且认为当足够小的情况下,网状结构将保持固体状态且能够抵抗外部压力,当外部压力上升至顶点,随后继续增加,便会破坏颗粒之间的连接,使颗粒重新排列,产生塑性变形,进而使其浓度升高。

因此,认为网状结构的压缩屈服应力随固体浓度的增加而增加,这是由于单位体积内颗粒数量越多,接触就会越多,从而造成网状结构强度越大。压缩屈服应力表征浆体的脱水阻力,即在一定压力或剪切力作用下,浆体可能达到的最大浓度。

1.2 凝胶浓度

底层物料的浓度随着压缩的进行而逐渐上升,当浓度达到顶点时,床层的内部絮状物连结在一起,形成一个网状结构,该结构可以抵抗外部的剪切作用并且强度较高,这个顶点就称之为凝胶浓度。

检测凝胶浓度就是对物料底部何时形成网状结构的研究,底部的颗粒将受上部物料重力产生的压应力。网状结构的强度随浓度的增高而增大,当网状结构强度与上部物料产生的压缩应力相等时,沉降停止。在沉降床层内部,固体浓度会随着深度的增加而增加。床层中的最大压缩应力也会随着初始浓度和高度的改变而改变,此时床层平均浓度也会发生改变。

1.3 剪切屈服应力

理论和实验研究表明,可以用宾汉姆模型或者H-B模型来表征全尾砂膏体的流变特性。认为膏体的应力——应变曲线为一条在切应力轴上有一截距τ0的直线或曲线,剪切应力只有超过这一应力时才开始流动,膏体产生流动时的临界应力称为剪切屈服应力。全尾砂膏体在发生流动时,剪切应力剪切速率之间的关系满足线性要求,便可采用宾汉姆模型来研究;但是当施加的外界剪切速率值较大时,呈现出类似于幂律流体等纯粘性非牛顿流体的行为,采用线性关系描述发生剪切流动阶段的膏体将不再合适。此时可使用三参数的H-B模型来描述,认为此类具有屈服应力的非牛顿流体其在超过屈服点之后,可以使用幂律流体的模型近似。当流动指数n＜1时,膏体具有剪切变稀特性;当流动指数n＞1时,膏体具有剪切增稠特性;当流动指数n=1时,曲线呈直线的形式,其斜率为膏体的塑性粘度系数,宾汉姆体模型为H-B模型的一种特征形式[16],流变方程为

式中:τ为剪切应力,Pa;τ0为屈服应力,Pa;η为塑性黏度,Pa·s;γ为剪切速率,s-1。

2 高压力下全尾砂压缩流变特性

2.1 多段压滤的理论基础和数学模型

采用理论分析的方法,利用压缩屈服应力参数开展高压力作用下尾砂浓密性能的研究。多压力过滤过程有以下几个阶段:初始滤饼形成、滤饼压缩、滤饼生长。

2.1.1 滤饼开始形成

在初始压力P1、初始浓度φ0时,自上而下的形成一个平均浓度为φ1的滤饼。在该压力下,滤液不断从底部滤布流出,滤饼厚度不断增加,平均浓度仍为φ1。此浓度和压力下,滤饼比阻为A1,

式中:P1为初始过滤压力,Pa;η为液体粘度,Pa·s;B为滤饼厚度,m;A1为压力P1时的滤饼比阻,m-2;t为过滤时间,s。

时间从t0至t1,滤液比容从V0至V。得到

式中:t为过滤时间,s;t0为初始过滤时间,s。

假设:(t0,V0)=(0,0)表示过滤初始状态

床层形成阶段,床层浓度与过滤时间的关系是线性的,而到了床层压缩阶段,床层浓度与过渡时间的关系是非线性的。无论是线性阶段还是非线性阶段,该曲线斜率代表了床层形成速度和床层压缩速度,斜率越小,速度越快。

2.1.2 滤饼压缩

在滤饼形成过程中

式中:V1为时间t1时的滤液比容;P2为第二过滤压力;A2为时间t1+t2时的滤饼比阻;φ2为压力P2时对应的滤饼浓度。

2.1.3 滤饼生长

在滤饼生长过程中

式中:A2为压力P2时的滤饼比阻;

2.2 参数计算方法

压缩屈服应力计算:

在理论分析的基础上,基于初始固体浓度和可浓密性能测试结果,可确定每个压力对应的极限平衡体积浓度计算方法

式中,h0为初始高度;h∞为各压力作用下的最终滤饼高度。

对于测试的各压力阶段,最终固体浓度浆体的压缩屈服应力等于施加的外部压力。因此,可浓密性能实验中,每个压力值产生一组数据点:(φ,P y(φ))。

2.3 实验方案

在压滤理论指导下,开展相关实验,对全尾砂高压力作用下的浓密性能进行测试。利用压滤实验柱,开展多段压力过滤实验,检测不同压力作用下,滤液流出速度和各压力作用下滤饼浓度。过滤压力分别为10 k Pa、20 kPa、30 k Pa、40 kPa、50 kPa、70 kPa、100 kPa,絮凝剂单耗为0 g·t-1、10 g·t-1、20 g·t-1、30 g·t-1,如图2所示。

图2 压滤实验柱Fig.2 Experimental column for filtration

2.4 全尾砂压缩屈服应力

基于前述分析,得到高压力下全尾砂浆体的压缩屈服应力,如图3所示。

图3 高压力下压缩屈服应力变化曲线Fig.3 Compressive yield stress variation curve at high pressure

当砂浆浓度低于0.3(53.7wt%)时,其网状结构所具有的压缩屈服应力为0～21 k Pa。当体积浓度增加至0.38～0.54(62.3～76wt%)之间时,所对应的压缩屈服应力呈数量级增加,达到15～100 k Pa。意味着如果需要达到较高的浓度,则必须提供较大的压缩应力,以破坏底流中强度较大的网状结构[17]。

3 剪切屈服应力测试

压缩和拉伸是剪切排水的两种基本模式,而产生排水的外力在于耙架提供的压缩应力和剪切应力[18]。利用压缩屈服应力表征网状结构的抗压强度,利用剪切屈服应力表征网状结构的抗剪强度。压缩屈服应力随浓度的增加呈指数形式上升。

3.1 桨式流变仪检测原理

检测方法如图4所示。屈服发生在由桨叶转子旋转产生的圆柱形表面附近,避免了壁滑效应,使浆体本身屈服[19]。

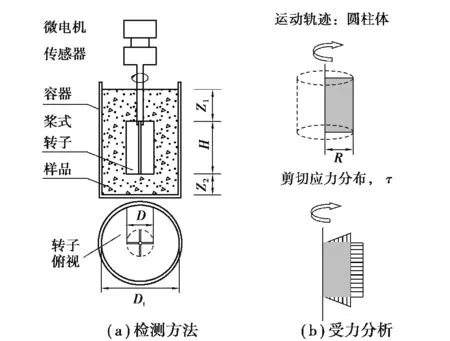
图4 桨式转子检测方法与受力分析Fig.4 Paddle rotor inspection method and force analysis

桨叶克服了浆体的屈服应力开始旋转,随着桨叶的旋转,在浆体周围一定范围内发生剪切作用,在旋转时扭矩与应力的关系如公式(11)所示。

式中,T为桨叶所受扭矩;τy为浆体的屈服应力;D为剪切圆柱体直径;H为剪切圆柱体高度。

3.2 Controlled Shear Rate法(CSR)

将桨叶完全侵入至浆体中,以相同的速度旋转,将检测出来的扭矩作为时间函数。图5为剪切应力时间曲线。从图中可以看出,C-D 区间包含了扭矩最大值,一旦屈服面的形状参数和剪切应力分布明确,就可以计算出屈服应力。

从图5可以看出有着2个屈服应力,分别发生在粘弹性终止阶段和应力时间曲线的峰值处,分别成为静态屈服应力(τy(s))和动态屈服应力(τy(d))。

图5 应力时间曲线Fig.5 Stress-time curve

3.3 实验方法

本试验采用流变仪进行检测,选用转子尺寸为H=4 cm,D=2 cm。选用500 ml的烧杯作为实验容器,D t=8.5 cm,Z1=5.5 cm,Z2=2 cm。实验采用会泽铅锌矿尾砂,平均粒径98μm,粒度较细。物料浓度分别为0.539(76 wt%),0.568(78 wt%),0.597(80 wt%),0.628(82 wt%)。

3.4 实验结果

将转子插入到位后,分别以0.05 s-1,0.5 s-1,1 s-1的剪切速率检测料浆的流变参数,得到的剪切应力时间曲线如图6所示。由图可知,剪切速率越高,得到的曲线波动越大。

图6 不同剪切速率时剪切应力时间曲线Fig.6 Shear stress-time curves at different shear rates

当采用较高的剪切速率检测时,高浓度料浆和低浓度料浆的流变曲线表现出不同的形式。如图6(a),图6(b)所示,0.5 s-1和1 s-1的峰值应力远高于0.05 s-1的结果。从图6(c),图6(d)可以看出0.5 s-1和1 s-1的峰值应力低于0.05 s-1的结果,说明剪切速率越大,峰值越小。

4 压缩屈服应力和剪切屈服应力的关系

将前述实验结果进行综合对比,绘制相同浓度下浆体剪切屈服应力和压缩屈服应力关系曲线,如图7所示。

图7 浆体屈服应力和压缩屈服应力关系Fig.7 Relationship between slurry yield stress and compressive yield stress

由图可知,浆体屈服应力为剪切应力,压缩屈服应力为压缩应力;浆体的压缩屈服应力、剪切屈服应力与浓度均呈指数关系。压缩屈服应力远大于剪切屈服应力。

因此,在相同条件下,剪切作用更易破坏絮团,是脱水的主要外部动力。在无耙的情况下,在浓密机内部仅有侧壁高度产生的重力压应变,而无侧向剪切应力,因此需要大大提高浓密机高度,形成深锥,以提供足够的压力破坏絮团。在任何耙架转速下,压缩屈服应力都随底流浓度的增大而增大。在实际工程中,浓密机的设计的核心内容在于两个关键参数:设备直径和搅拌扭矩。浓密机直径选择过小会造成处理能力、底流浓度不达标;过大则会造成投资浪费。深锥浓密机的优势在于由于床层高度大、导水杆数量多,从而易于获得高浓度的底流,但会带来的不利表现就是搅拌耙架扭矩过大。为此,在工程实践中可通过设置耙架或增加浓密机高度的方法来提高底流浓度。

产生上述现象的原因是颗粒群——液体散结构的物理力学特点决定的。根据吴爱祥等人的研究,散体结构的抗压强度大于其抗剪强度。其中,抗剪强度受多因素支配,包括:颗粒间的摩擦、剪胀等,如图8所示。