磁流变调谐质量阻尼器在海上风机振动控制中的应用

杨 毅,冷鼎鑫,徐 凯,刘贵杰,田晓洁,谢迎春,王泓晖

(中国海洋大学 工程学院,山东 青岛 266100)

风能作为一种可再生的清洁能源是绿色能源的代表。海上风力发电是一种对风能进行有效开发利用的新技术,已成为风力发电的主流发展趋势[1-2],在全球范围受到越来越多的关注。海上风力机采用新型复合材料后比以前更大更轻,这些大型柔性结构容易受到海洋环境外部振动源影响。为了保证海上风电机组的安全运行,需要对风电机组的动力响应进行振动控制。目前,国内外学者对海上风机塔架/叶片的振动控制主要采用在海上风机塔架顶部(即机舱内)安装被动调谐质量阻尼器(TMD)[3-5],通过抑制塔顶位移最大的塔架基本振型,达到对风机塔架的减振效果,该方法适用于海上风机在风、波浪低频载荷下的振动控制,此时风机塔架的主要激发模态为塔顶位移的第一阶主振型。世界上很多已建或在建海上风电机组位于地震多发地带,在风、波浪、地震多种载荷作用下,海上风机的高阶模态振型被激发,系统呈现多个不同阶次固有频率的振动特征,若仍采用针对常规工况(风/浪载荷)设计的被动TMD 对风机减振,效果会大大降低甚至造成抑振失效。

针对此类问题,有学者[6-9]提出了多重调谐质量阻尼器(MTMD),由2个或2个以上质量较小的TMD分别安装在塔筒的不同位置以应对不同的振动特性,结果表明控制效果优于单一TMD;还有学者提出半主动控制方法,通过采用智能材料驱动和自适应控制算法,衰减海上风机在多载荷激励下的振动响应,如:李静等[10]提出了磁流变阻尼器与模糊控制算法结合的半主动控制模型,应用于地震和风载荷作用的海上风机结构,结果表明,采用磁流变阻尼器能够有效减小地震和风载荷作用下的风机结构的加速度和位移响应;闫石等[11]基于形状记忆合金(SMA)的超弹性效应,设计了针对风机塔架结构的耗能减振装置,通过对比塔架位移和加速度响应证明了SMA-TMD 的有效性。

文中应用一种基于磁流变弹性体的变刚度调谐质量阻尼器,开展导管架式近海风机在风、波浪和地震多种载荷联合作用下的振动控制研究。对MRE-TMD 的结构设计和工作原理进行了分析,提出了针对风机减振需求的关键参数设计;建立了导管架式海上风机-TMD 的动力学模型,基于频率跟踪算法,评估了MRETMD 对海上风机动力学响应的控制效果。

1 MRE-TMD结构和工作原理

1.1 磁流变弹性体材料特性

磁流变弹性体的弹性模量可以随着磁场的改变而改变,当磁场撤去后可立即恢复到初始状态。基于这种磁控特性,磁流变弹性体已广泛应用于变刚度智能吸振器及隔振器。

根据偶极子模型[12]可知,MRE中的铁磁颗粒在磁场作用下发生相对运动,导致材料剪切模量变化,磁致剪切模量为[13]

式中,a是铁磁粒子半径;r0是粒子间距离;φ是铁磁颗粒体积分数;为外部磁场强度;μ0是真空导磁率,μ0=4π×107(Hm-1);β= (μp-μ1)/(μp+2μ1)≈1;μp为铁磁颗粒的相对导磁率;μ1 为硅橡胶的相对导磁率;ξ=。

磁流变弹性体材料在零磁场下的剪切模量Gzero为[14]

式中,G0为基体弹性模量。

MRE的有效剪切模量为

1.2 MRE-TMD结构和工作原理

海上风机在风、波和地震荷载作用下,塔架结构顶部与机舱将出现明显位移,设计的MRE-TMD 在机舱应承受较大的横向应变;此外,TMD 与主结构的质量比一般设置在1%～8%之间[7],海上风机主结构的质量以百吨计入,意味着MRE-TMD 需要提供足够的竖直承载力。为了满足OWT 振动控制要求,文中采用多层MRE变刚度TMD,如图1所示,其由MRE 隔振器[15]连接质量块构成,通过顶端质量块运动提供惯性力来进行风机的振动控制。

图1 MRE-TMD装置Fig.1 MRE-TMD device

作为MRE-TMD 系统的核心部件,MRE在剪切工作模式下的刚度可表示为

式中:GMRE为MRE 的剪切模量;A为MRE 的横截面积;h为橡胶层的厚度;n为该装置中磁流变弹性体层数。

在多载荷联合激励下,海上风机主要被激发一阶和二阶主振型模态,并且模态参与比在80%以上[7]。因此,文中主要针对风机的前两阶主频,设计MRE-TMD 的变频范围,[λopt·f1,λopt·f2],其中,λopt=为MRE-TMD 系统的最优频率比[16],f1和f2分别为风机结构的一阶主频和二阶主频,具体参数如表1所示。MRE-TMD 的参数为

表1 导管架式海上风机前两阶固有频率Table 1 First two natural frequencies of jacket supported offshore wind turbine

式中:μ为质量比,文中取μ=5%;f i为MRE-TMD 变频范围内的频率;ζ为阻尼比。

2 海上风机MRE-TMD系统动力学建模

2.1 海上风机模型

研究对象为NREL公司5MW 导管架式海上风机[7-9],主要参数如表2所示,导管架式海上风机模型如图2所示。

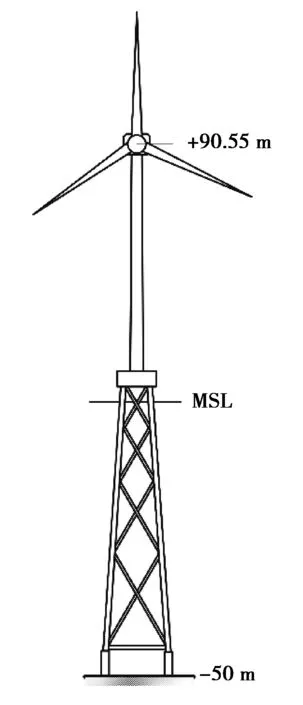
图2 导管架式海上风机示意图Fig.2 Schematic diagram of jacket supported offshore wind turbine

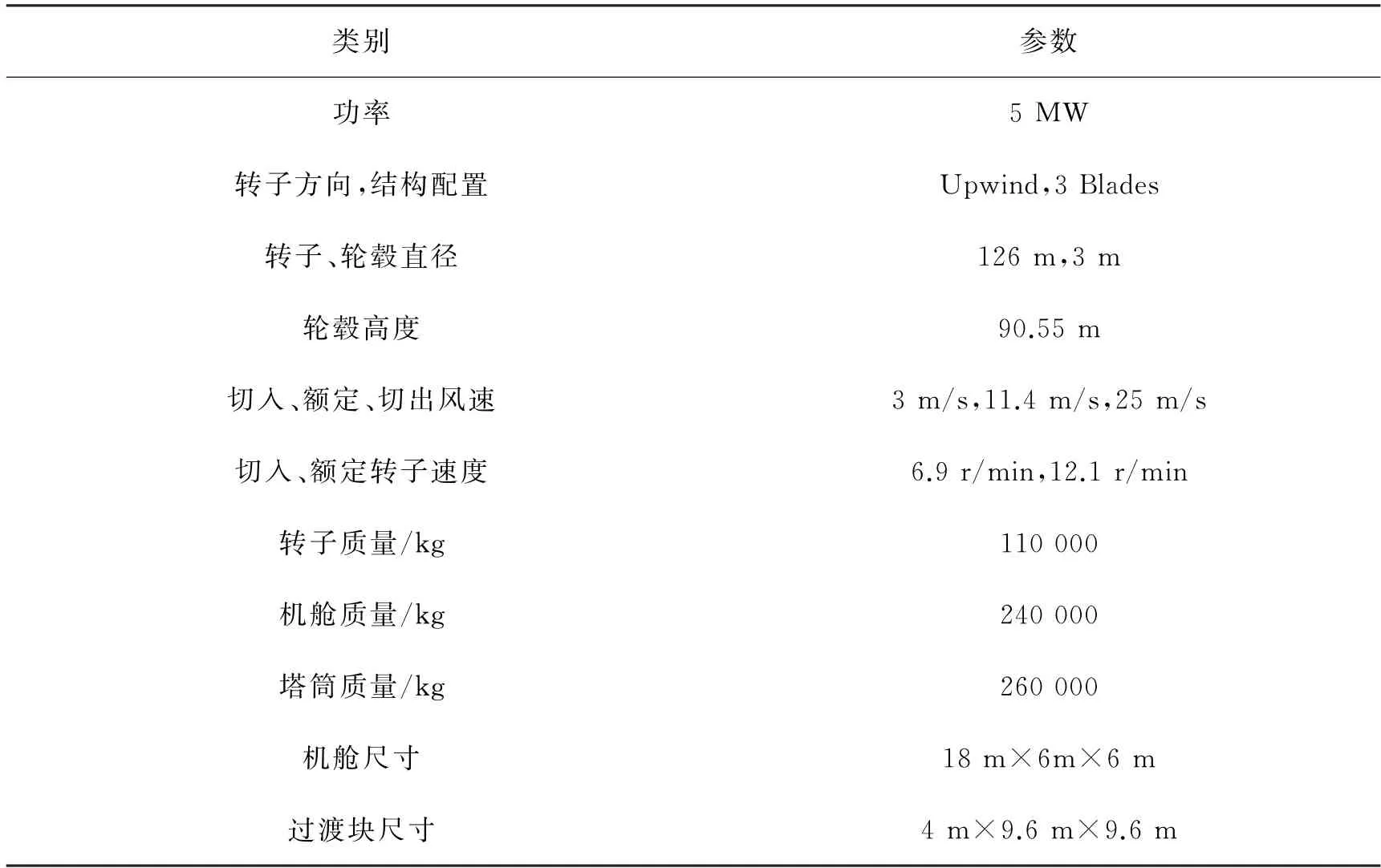
表2 NREL 5MW 导管架式海上风机参数Table 1 Parameters of NERL 5MW jacket supported offshore wind turbine

应用有限元软件ANSYS,建立NREL 5MW 导管架式海上风机有限元模型。叶片和机舱简化为集中质量,单元类型为MASS21单元,塔筒采用SHELL181单元,连接塔筒和导管架基础的过渡块采用SOLID95单元,导管架结构采用PIPE59单元,泥桩结构采用PIPE16单元。建立的导管架式海上风机有限元模型如图3所示。

图3 导管架式海上风机有限元模型Fig.3 Finite element model of jacket supported offshore wind turbine

2.2 海上风机环境荷载分析

海上风机工作环境复杂,受风、冰、流、波浪和地震等荷载作用。文中主要研究风载荷、波浪载荷和地震3种载荷的联合作用。

2.2.1 风载荷

由于将风机模型简化为多自由度集中质量模型,只考虑作用在风机塔筒上的风载荷,不考虑风机叶片上的作用力。作用在风机塔筒上的风载荷为

式中:Cd为空气阻力系数;ρa为空气密度;A为塔筒的迎风面积;v-(t)为平均风速;v＇(t)为脉动风速,采用Davenport脉动风速谱通过谐波叠加法模拟求得;仿真的风载荷工况为机舱位置平均风速25 m/s。

2.2.2 波浪载荷

波浪是一个随机过程,组成波浪的能量分布可以用波谱来描述。利用JONSWAP 谱模拟波浪高程。JONSWAP谱[17]为

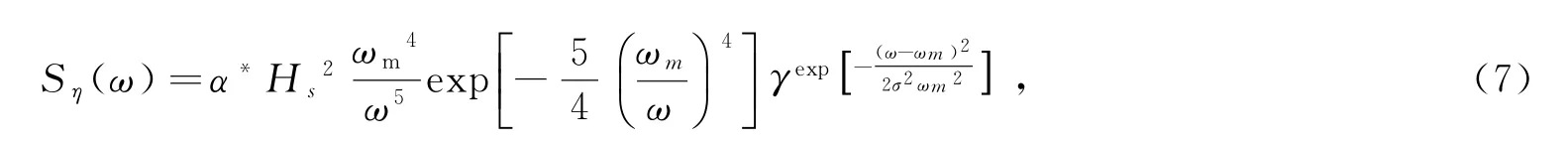
式中:Hs为波高;γ为峰值系数(文中取γ=3.3);g为重力加速度;σ为峰形因子和α*计算如下:

根据莫里森方程,单位高度dz上的波浪力为

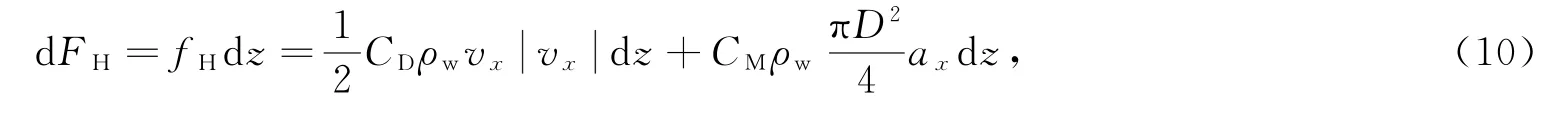
式中,CD和CM分别为拖曳力系数和惯性力系数,取CD=0.65,CM=2,ρw为海水密度,取1 030 kg/m3。波浪工况为,Hs=9.4 m/s,Tp=10.47 s。

2.2.3 地震载荷

处于地震带的海上风机,地震荷载是极端工况载荷。以Kobe(1995)为地震波输入,其地震加速度时程和加速度谱如图4和图5所示。

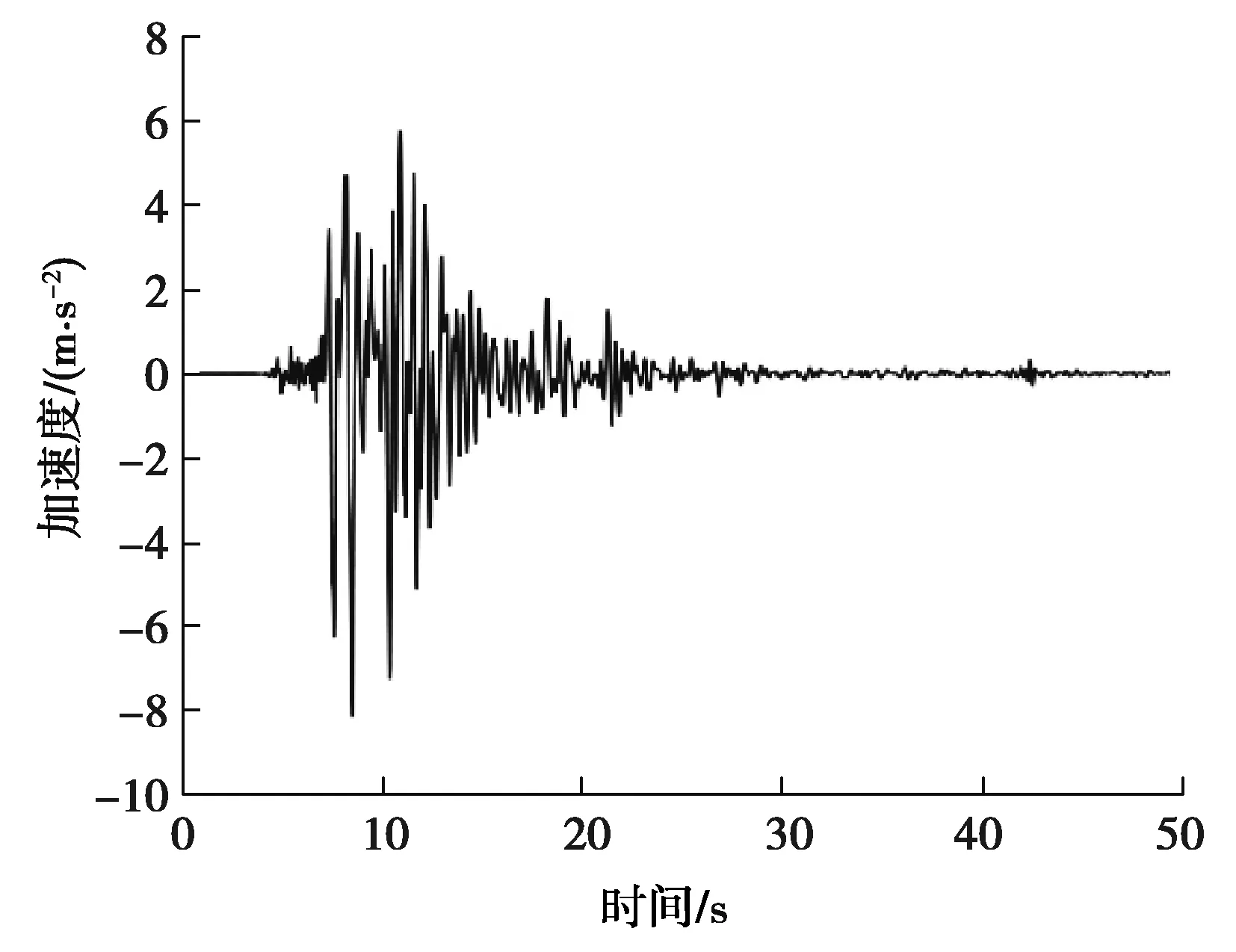
图4 Kobe地震加速度时程Fig.4 Acceleration time history of Kobe earthquake

图5 Kobe地震加速度谱Fig.5 Acceleration response spectra of Kobe earthquake

2.3 海上风机-MRE-TMD系统动力学建模

建立风机-MRE-TMD 动力学模型,运动方程为

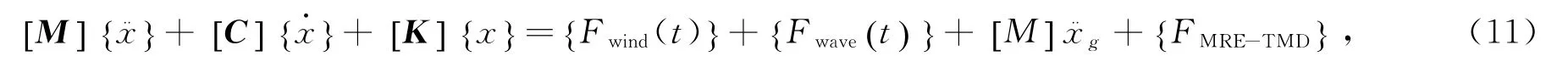
式中:{x},分别为位移向量、速度向量和加速度向量;[M],[C],[K]分别为风机-MRE-TMD 系统的质量矩阵、阻尼矩阵和刚度矩阵;{Fwind(t)}为风载荷向量;{Fwave(t)}为波浪载荷向量为地震加速度;{FMRE-TMD}为MRE-TMD 产生的作用力。

图6为MRE-TMD 安装在风机机舱内的示意图。

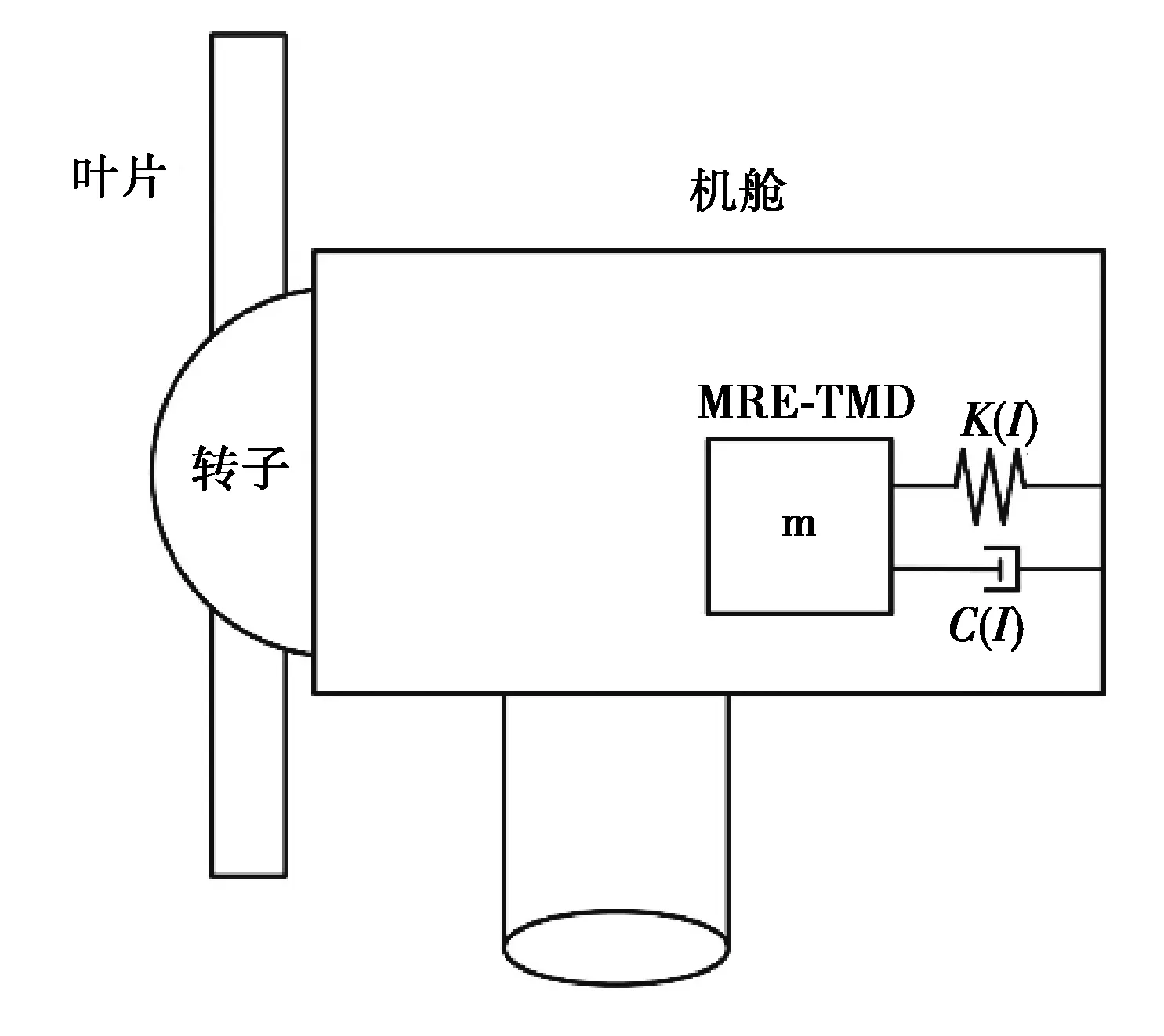
图6 MRE-TMD在机舱的布局示意图Fig.6 Schematic diagram of MRE-TMD in the nacelle

根据结构设计原理和海上风机主要参数,可以确定MRE-TMD 的变刚度范围,[kMRE-TMD-min,kMRE-TMD-max]。文中MRE-TMD 关键参数如表3所示。采用多次非线性拟合[18-19],获得刚度、阻尼与电流之间的关系。其中,作为对比的被动TMD 是根据系统的一阶主频设计得到的,其各个参数为MRE-TMD 在刚度最小时的参数。

表3 MRE-TMD参数Table 3 Parameters of MRE-TMD

2.4 半主动控制系统

TMD 装置由质量、阻尼器和附在结构上的弹簧组成,MRE-TMD 是基于MRE 材料的TMD 装置,其刚度和阻尼由MRE提供。该装置的主要特点是通过改变外加磁场来改变MRE 的刚度进而调节MRE-TMD装置的频率,使其频率跟随风机结构的主频,从而在外部激励作用时通过质量块的振动耗能,达到降低结构振动的目的。

文中基于短时傅里叶变换(short-time fourier transform,STFT)对风机塔筒顶层(机舱位置)响应的频率进行识别,实时计算MRE-TMD 所需刚度,根据MRE刚度与电流的对应关系确定控制电流的大小,最后输出时变控制力对风机进行减振。

短时傅里叶变换的基本原理为[20]

式中:x(τ)为源信号;h(τ-t)为窗函数。

t时刻功率谱密度为

因此,t时刻的瞬时频率为

基于短时傅里叶变换半主动控制,尽可能实时识别风机塔筒顶端的响应频率,根据频率实时调节MRETMD 的刚度。实时控制流程如图7所示。

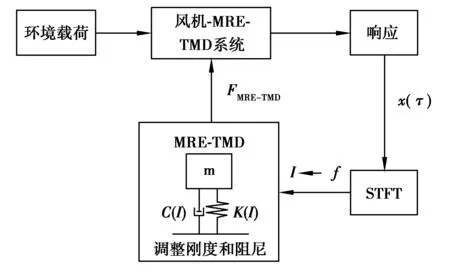
图7 半主动控制流程Fig.7 Flowchart of semi-active control

3 海上风机振动控制结果

海上风机工作环境复杂,容易受到风、波浪、地震等载荷的作用,文中研究对象为固定式海上风机,单独的波浪载荷对风机的影响相对风载荷和地震载荷来说较小,因此,仿真了在风、地震单独作用及风浪联合作用的工况下,海上风机在被动和半主动控制下的响应时程结果如图8～图11所示。

图8 风载荷作用下的塔筒顶层位移响应时程Fig.8 Tower top displacement time history under wind loading

由图8和图9的时程结果可知,风载荷单独作用和风浪作用下,风机塔筒顶层位移半主动控制略优于被动控制,这个结果是合理的,因为风载荷和波浪载荷是低频载荷,只会激起风机的一阶振型,被动TMD 就是根据系统的一阶主频设计的,有很好的减振效果。从图10和图11的仿真结果可知,在地震单独作用下,半主动控制效果明显优于被动控制,这是由于地震属于宽频载荷,会激起风机的高阶振型,此时,半主动MRETMD 通过变刚度调节,实时跟踪风机系统的频率,达到了更好的减振效果。为了对海上风机进行详细分析,从时域和频域对海上风机在风、波浪和地震3种载荷联合作用下的被动控制和半主动控制的仿真结果进行了分析,如图12～图14所示。

图9 风浪联合载荷作用下的塔筒顶层位移响应时程Fig.9 Tower top displacement time history under wind and wave loadings

图11 地震作用下加速度响应时程Fig.11 Acceleration time history under earthquake

图12 位移响应时程Fig.12 Displacement time history

图13 加速度响应时程Fig.13 Acceleration time history

图14 加速度幅值对比Fig.14 Comparison of acceleration amplitude

在3种载荷作用下,风机塔筒顶层和塔筒底层的位移、加速度在被动控制和半主动控制2种方式下的响应时程结果,如图12和图13所示。为说明文中风机-MRE-TMD 系统的半主动控制效果,以被动控制结果作为参考对比。由图12和图13结果可知,半主动控制下的塔筒顶层和底层的位移和加速度响应均小于被动控制下对应的响应结果。由表4和表5可知,被动控制对塔筒顶层和底层的位移减振率分别为50.92%和22.35%,对塔筒顶层和底层的加速度减振率分别为24.53%和4.78%。而在半主动控制下,位移减振率为70.4%和35.71%,加速度减振率分别为99.97%和29.43%,半主动控制减振效果明显优于被动控制。

表4 位移均方根(RMS)Table 4 RMS displacement

表5 加速度均方根Table 5 RMS acceleration

为了进一步验证MRE-TMD 在地震激起的高阶模态下的响应的减振效果,风机塔筒顶端和底端的加速度幅频响应如图14所示。当有地震作用时,风机的高阶模态会被激发,因此对于高阶模态响应的抑制至关重要。从图14可以看出,半主动控制对于抑制风机系统的二阶模态响应效果明显,根据表6中结果,被动控制和半主动控制对于风机系统一阶模态的控制效果相当,降幅均在80%以上,而对于第二阶模态响应,半主动控制对塔筒顶层和底层的加速度幅值的降幅分别为64.3%和48.81%,而被动控制的效果不明显,分别为3.88%和5.79%。结果表明,MRE-TMD 半主动控制能够有效减轻多种载荷作用下风机系统的振动。

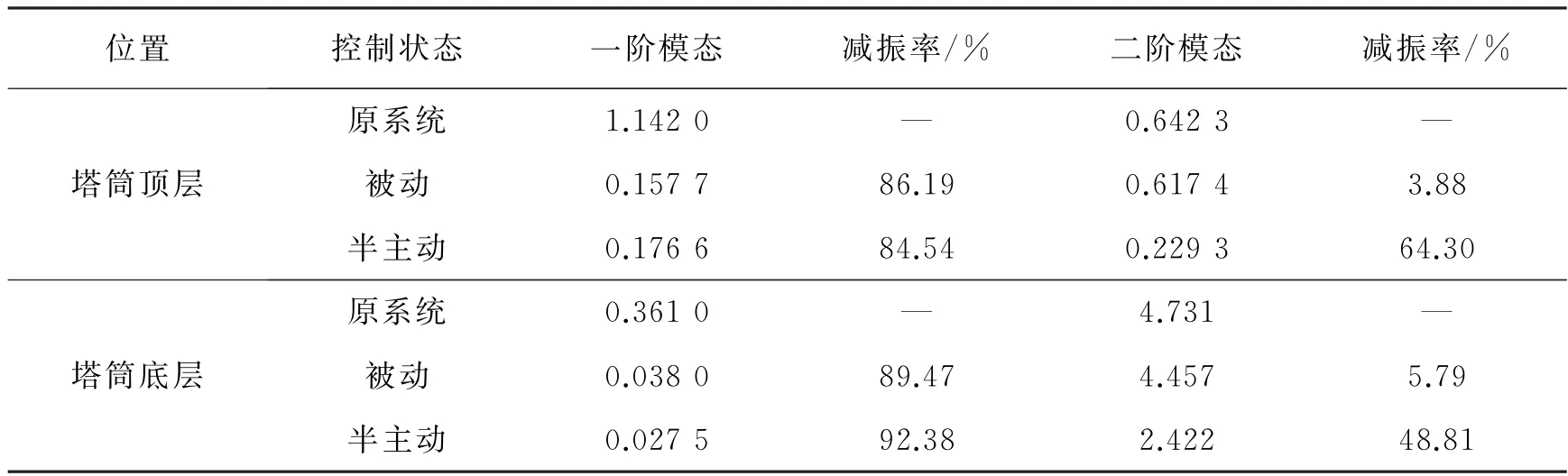
表6 加速度幅值Table 6 Amplitude of acceleration

4 结束语

通过磁流变弹性体调谐质量阻尼器MRE-TMD 对导管架式海上风机进行了半主动控制,对比分析了被动控制和半主动控制2种方式作用下,海上风机在风、波浪和地震3种载荷作用时的位移和加速度响应;结果表明,MRE-TMD 半主动控制可有效降低风机的动力学响应振动,塔筒顶层和底层的位移RMS减振率分别为70.4%和35.71%,加速度幅值一阶减振率分别为84.54%和92.38%,二阶减振率分别为64.3%和48.84%,对于地震激发的高阶模态的减振效果较被动TMD 效果更好。