锂电池电极纳米颗粒和粘结剂在充电放电循环中的应力计算

张富亮 ,阳如坤 ,张 强 ,刘金铭 ,何 红 ,于洪杰

(1.北京化工大学 机电工程学院,北京 100029;2.深圳吉阳智能科技有限公司,广东 深圳 518101)

锂离子电池作为可充电电池在动力电池领域发展迅速,使大容量、更高循环次数电池的需求和发展愈发突出。锂离子电池核心组成部分有正负电极活性材料和电解液,电池充电工作过程是锂离子从正极材料脱出嵌入负极材料的过程,而放电过程与之相反,期间锂离子不破环电极活性材料的晶格结构,仅引起晶格间距的变化,导致活性材料宏观体积的变化,从而在电池内部产生应力。

粘结剂是电池正负极板制造过程的重要材料,与其他材料按一定比例将颗粒状电极活性材料粘结起来形成电极复合膜,使电极活性材料、导电剂和电极集流体之间具有良好的电子导电网络。有研究显示粘结剂对锂离子电池的循环性能有重要的影响[1],有许多研究聚焦改进现有的粘结剂或者开发新的粘结剂配方,Munaoka等[2]研制自愈合聚合物作为粘结剂用于改善锂离子电池硅负极循环性能;Rajeev等[3]开发了壳聚糖接枝聚苯胺共聚物(CS-g-PANIs)作为硅阳极聚合物粘合剂材料;Yang等[4]为了保持高电子传导性、机械粘附性、延展性和电解质吸收开发了一种具有多功能的粘结剂聚合物。但这些研究很少关注粘接剂的基本应力应变行为。粘结剂在锂离子电池中的用量虽然较少,但它却是整个电极力学性能的主要承担者,对电极的生产制造和电池的电化学性能有重要影响[5-6]。粘结剂的机械失效是造成锂离子电池电极容量衰减的主要原因之一。在充电/放电过程中,活性颗粒的体积变化会在粘结剂粘结面处引起显著的应力应变[7],达到某一阈值时,粘结剂将经历永久变形,导致一些活性粒子产生电隔离,阻止它们积极参与电化学反应,从而导致不可逆的电池容量损失。当前的多种粘结剂中,聚偏氟乙烯(PVDF)有较好的抗氧化还原能力,热稳定性和易分散等优点,是目前锂离子电池中最常用的粘结剂。

电极材料,相比传统的石墨基电极(比容量为372 m Ah/g),硅拥有更高的理论比容量3 579 m Ah/g,是理想的优质高密度储能负极材料。然而,在锂嵌入/脱出反应中,硅的大体积膨胀(约300%)收缩特性不仅会导致复合电极活性颗粒内产生应力,甚至可能导致活性颗粒断裂,粘结剂从界面剥离,最终导致电池失效,一直是制约其广泛使用的主要障碍。

目前开展的粘结剂方面的研究主要是实验测试粘接强度,如撕裂和刻划测试[7-9],这种宏观尺度的测试方法可以半定量地评价粘结强度[10-12],但是对于微米及纳米尺度的活性颗粒间的粘结强度很难计算。研究发现纳米硅颗粒直径小于150 nm 时在电化学循环过程中能适应硅的大体积膨胀不易发生颗粒断裂[13],Hertzberg等人报道了锂离子嵌入/脱出第一个周期中硅管在纳米空间内形状的不可逆变化[14],Takahashi等[15]将粘结剂层假设为线弹性材料,研究了石墨/聚偏氟乙烯复合电极的机械失效,Higa[16]研究了嵌锂硅颗粒与粘结材料之间的力学相互作用,Lee等[17]结合电化学 力学模型和内聚区模型研究嵌锂过程中的界面脱粘,Takahashi等[18]研究了石墨/聚偏二氟乙烯(PVDF)复合电极的机械失效模式;Lee等[19]研究了粘结剂特征对电极机械响应的影响。以上研究都将粘结剂层假设为为线弹性材料,这样假设会使计算结果出现一定偏差,甚至会造成计算结果与实际不相符。Mattos[20]的实验表明电池中最常用的粘结剂PVDF不是简单地线弹性行为,而具有强烈的非线性特点,Nadimpalli[21]的实验测量表明PVDF 符合弹粘塑性模型,其模拟研究表明将粘结剂处理为线弹性模型会到导致复合电极模型的计算不准确。也有研究者用Neo-Hooke超弹性模型描述粘接剂的力学行为[22-23]。Vinogradov等[24]经过测试发现PVDF粘结剂符合粘弹性行为,但是将充放电过程发生大形变的粘结剂加入复合电极中计算循环性能的研究较少。因此选择硅颗粒与PVDF粘结剂作为研究对象,通过有限元方法,研究锂离子电池在充电/放电过程中活性材料硅和粘结剂PVDF的应力应变演化,以便找到适合描述粘结剂形变的本构模型,探索粘结剂含量对于粘结剂/硅界面应力的影响,进一步理解锂离子电池工作失效机理,提高其使用寿命、指导粘结剂选择和有助新型粘结剂材料的开发。

1 粘结剂材料的本构方程描述

对于粘结剂材料,目前多数学者均假设为线弹性材料[12,25],满足广义胡克定律率。

式中:σij为应力分量;εij为应变分量(i=1,2,3);λ为常量;G为剪切模量。

PVDF膜的单轴拉伸等实验研究表明粘结剂材料本身较为复杂[26-27]。常温下PVDF 为半结晶聚合物,杨氏模量大约在1.5 GPa～2.5 GPa之间,PVDF聚合物在吸收电解质有机溶液并熔融以后,杨氏模量降低而形成橡胶状固体。因而粘结剂的本构行为假设为超弹性或粘弹性较符合实际,Neo-Hookean超弹性模型应变能密度函数W如公式(2),粘弹性本构方程,则以材料的无量纲松弛模量表示的prony级数为公式(3)为

式中:I1是左Cauchy-Green变形张量的第一不变量;J是变形梯度的雅可比行列式。

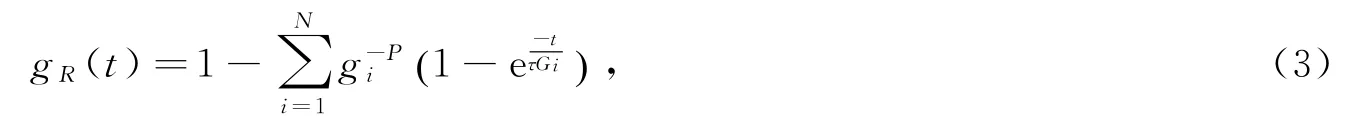
式中:g R(t)是松弛模量;N、、τG i是材料参数。也有对PVDF 蠕变特性测试[28]发现PVDF 粘结剂行为为粘弹性行为,可用粘弹性本构模型来描述。

虽然线弹性假设计算方便,但对于较复杂的粘结剂,特别是大体积膨胀收缩负极硅,其间的粘结剂被压缩变形量较大,可能超过80%,再采用适用于小形变的线弹性假设显得过于简单,不足以反应粘结剂的流变学行为,容易造成误差大,从而导致结果不准确性,因此研究选择粘弹和超弹性本构方程,同时与线弹性对比,根据PVDF的力学实验[26],其应力应变曲线拟合,得到以下PVDF的线弹性本构模型参数杨氏模量和泊松比、Neo-Hookean超弹性本构模型参数和粘弹性数模型参数,如表1所示。从表中可以看出,用prony级数表示的粘弹性模型在3个模型中与实验曲线的吻合最好,相对误差最小,采用该模型更符合实际。

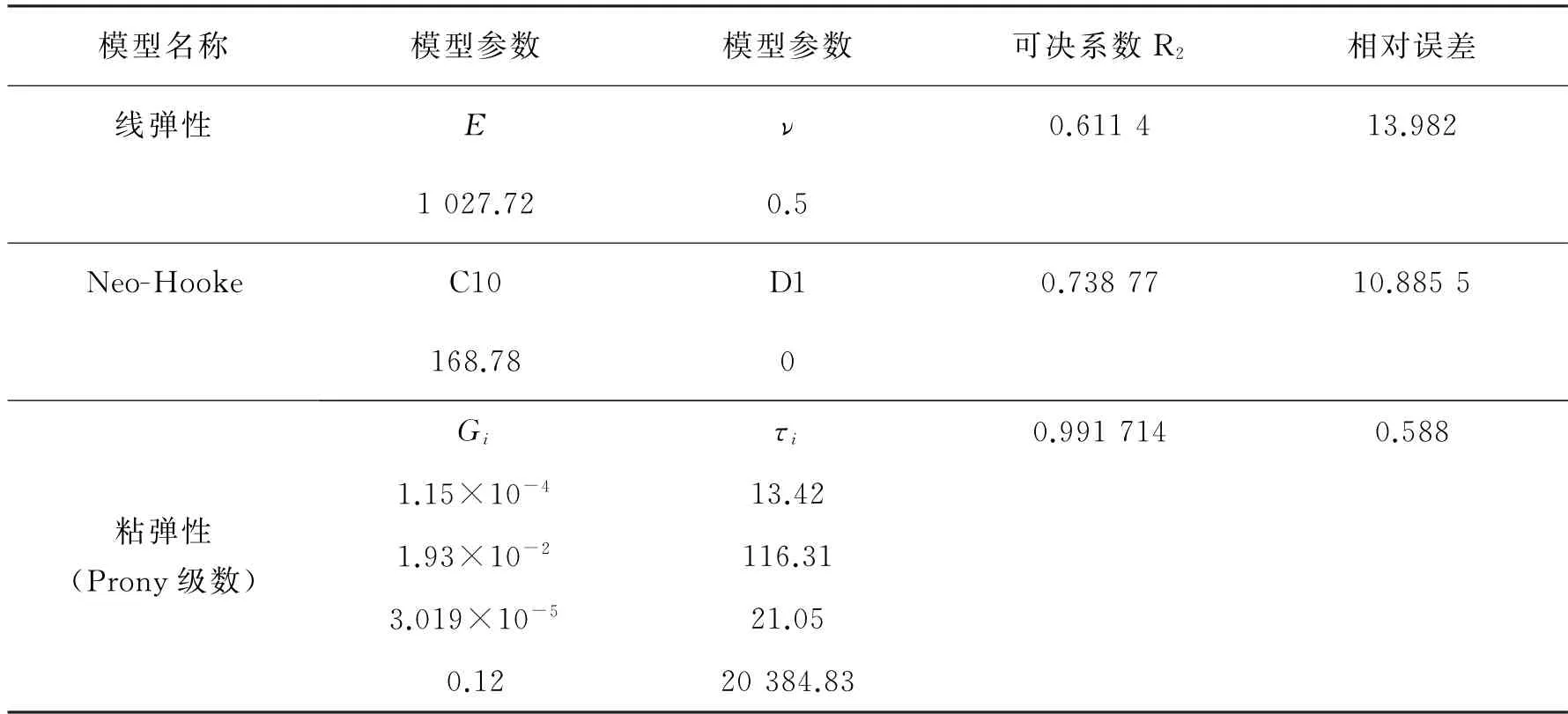
表1 PVDF粘结剂的模型和参数Table 1 Model and parameters of PVDF binder

2 锂离子扩散方程与求解

锂离子遵守扩散方程和弗里克扩散定律

式中:j为扩散电流;D为扩散系数;t为时间;C和C分别为锂离子浓度和归一化的锂离子浓度。方程(4)、(5)与热传导方程和傅里叶热传导定律的表达式相似

式中:q是热流密度;k是导热系数;u温度;c p和ρ分别是导体的比热和密度。对比方程(4)、(5)和(6)、(7),可以发现,如果设置k=D和c p·ρ=1,则扩散电流j、扩散系数D和锂离子浓度C分别对应于热流密度q、导热系数k和温度u。由此锂离子扩散问题可以等价于传热问题的求解,可以借助传热工具等效求解锂离子在极片硅颗粒间的扩散,充电和放电过程分别对应于加热和散热过程。

根据体积膨胀和锂化度之间的关系,V=V0(1+βC),其中β为体膨胀系数,β取2.7[9],由此可以得到硅的线膨胀系数α

采用有限元方法中的温度位移耦合模式等效锂离子嵌入和脱出时硅的膨胀。硅的锂化杨氏模量Es、锂化泊松比νs屈服应力σy可以通过完全锂化和纯硅的杨氏模量E1、E0和泊松比v1和v0屈服应力计算[28-30]

3 硅颗粒和粘结剂在充电和放电过程的有限元模拟

为了计算复合硅电极颗粒和粘结剂在充放电循环过程中的应力,不考虑硅颗粒因膨胀、收缩产生的应力而引起锂的不均匀扩散。假定粘结剂层均匀的分布在2个活性颗粒之间;影响锂扩散的因素只有锂离子浓度,在锂浓度梯度的作用下锂离子自由扩散,取扩散常数[26]D=10-16(m2·s-1);由于实际中的粘结剂往往添加了诸如乙炔黑的导电添加剂,并且被电解液浸泡,因此认为粘结剂是良好的锂离子导体,即锂离子通过粘结剂层完全没有阻碍,即颗粒表面的锂离子浓度与粘结剂外表层的锂离子浓度相同。建立如图1所示的轴对称有限元模型。选取活性颗粒半径[31]为R=100 nm,粘结剂层厚40 nm,计算恒定通量锂离子扩散情况。

图1 硅颗粒和有粘结剂层的复合硅电极轴对称有限元模型Fig.1 Axisymmetric finite element model of composite silicon electrode with silicon particles and adhesive layer

3.1 硅颗粒在充电放电过程的应力变化

在硅颗粒表面施加恒定的锂通量,硅在室温下的理论容量Cmax=29.89×109C/m3,以0.096 5 A/m2的电流密度将硅锂化到平均浓度=0.425,充电过程中硅颗粒的Mises应力变化如图2,Mises应力是基于3个主应力的等效应力。硅颗粒自由端的半径R1、颗粒间接触半径R2在3次充电放电循环中的变化见图3和图4所示。硅颗粒间的接触应力计算结果见图5所示,接触应力方向为颗粒接触面的法线方向。

图2 第一次充电放电循环中活性颗粒经历的应力变化云图Fig.2 Cloud diagram of stress change experienced by active particles in the first charge discharge cycle

图3 颗粒自由端半径R1 在3次充电放电循环中的变化Fig.3 Variation of particle free end radius R1 in three charge discharge cycles

图4 硅颗粒接触半径R2 在3次充电放电循环中的变化Fig.4 Variation of contact radius R2 of silicon particles in three charge discharge cycles

当2颗粒相互挤压应力超过屈服应力时,两活性硅颗粒便会发生永久的塑性变形如图2(c)、(d)、(e)。充电前自由端半径R1、接触半径R2与粒子的初始半径R相等,随着充电过程进行硅颗粒的自由端半径R1膨胀,而接触半径由于颗粒接触界面的存在基本保持不变,见图3和图4所示。多次循环中的2颗粒间最大的接触应力发生在第一个循环中,随后循环中的最大接触应力较第一次循环小,见图5所示,随着锂浓度引起的颗粒膨胀变化导致颗粒间相互作用的接触应力变化,在第一次充电过程中锂浓度增加使膨胀颗粒相互挤压加剧,接触应力表现为急剧升高达到峰值,接触应力超过屈服应力后会发生硅颗粒永久塑性变形,产生能量损耗;随着放电过程锂浓度的下降,接触应力降低,当相互挤压的硅颗粒脱离接触时,接触应力迅速下降,因此锂电池的第一次充电过程是最危险的过程,在第一次充电过程的硅颗粒模型里硅的相互挤压产生的很大接触应力会引起整个电极乃至整个锂电池都会产生大应力,这极易引发活性颗粒的粉碎性破裂,造成锂电池的失效。巨大的塑性应变不仅会使电池容量造成损失,还可能会造成电池内阻增大,枝晶析出等一系列问题。

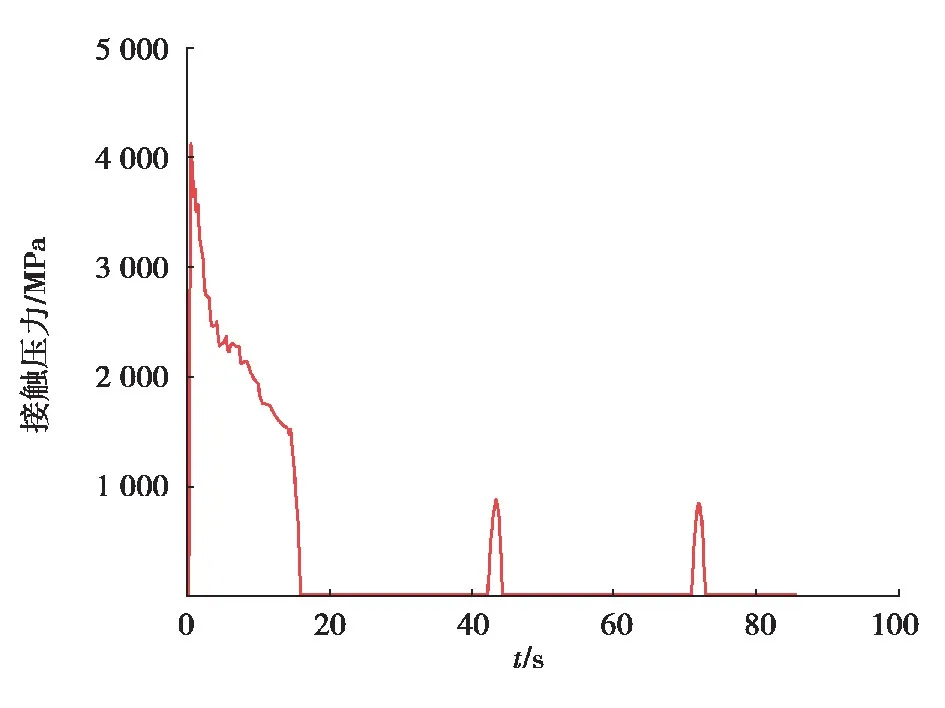
图5 硅颗粒间接触应力在3次充电放电过程的变化Fig.5 Variation of contact stress between silicon particles during three times of charge and discharge

3.2 粘结剂/颗粒界面的应力变化

充电放电过程中粘结剂用3种流变本构模型(线弹性、超弹性和粘弹性)的计算得到的应力和应变、硅颗粒与粘结剂接触界面的厚度结果分别见如图6～图9所示,这里分别以2.79×10-2A/m2、8.37×10-2A/m22种电流密度将硅锂化到平均归一化浓度=0.083、=0.238,粘结剂层的厚度指2个硅颗粒间的最近的距离,粘结层初始厚度h0为40 nm。

图6 三次充电放电循环过程的界面接触应力(线弹性、NeoHooke超弹性和粘弹性三种本构模型)Fig.6 Interfacial contact stress during three charge discharge cycles(three constitutive models:linear elasticity,neohooke hyperelasticity and viscoelasticity)

从图6粘结层接触应力的结果可以看出,3种流变模型中线弹性模型的应力变化很大,Neo-Hooke超弹性模型得到的应力变化次之,粘弹性模型得到的应力变化最小。从图6(a)可以看到充电过程t=5 s时,线弹性本构方程计算得到的Mises应力约是超弹性本构方程结果的2倍,可见选用不同的本构方程对应力预测会产生很大的影响,采用符合粘合剂流变行为的本构方程很重要,图6中粘弹性模型得到的应力变化小,其大小量级与实验结果相符[23],因此选用粘弹性模型描述PVDF粘结剂的流变行为比较符合实际,即形变较大时采用粘弹性本构方程比采用适于小形变的线弹性本构方程更合理。粘弹模流变类粘结剂承受的应力小于超弹性类和线弹类流变行为的粘结剂,这一点可供锂电池粘结剂选择时参考。

从图7、图8可以看出硅的平均锂化程度C=0.083时,充电使粘结剂层经历较大的变形,粘结层的压缩量近80%,从而使粘结剂层出现了较大的应力,并且在靠近底部接触点附近的圆环形区域产生的应力和应变大于底部接触中心点的应力和应变,见图8和9(c)和(h)t=10 s,计算结果可以解释粘结剂先从最大环状应变位置开始脱落的原因。如果粘结剂的弹性小,就会在粘结剂/硅界面处产生很大的接触应力,影响粘结剂和硅颗粒间界面机械损伤性能,可见粘结剂的性能对界面应力有显著影响,无疑力学性能优良的粘结剂是锂电池技术进步所需的。

图7 3次充电放电循环过程中粘结剂层的厚度变化(粘弹模型,电流密度8.37×10-2 A/m2)Fig.7 Thickness change of adhesive layer during three charge discharge cycles(viscoelastic model,current density 8.37×10-2 A/m2)

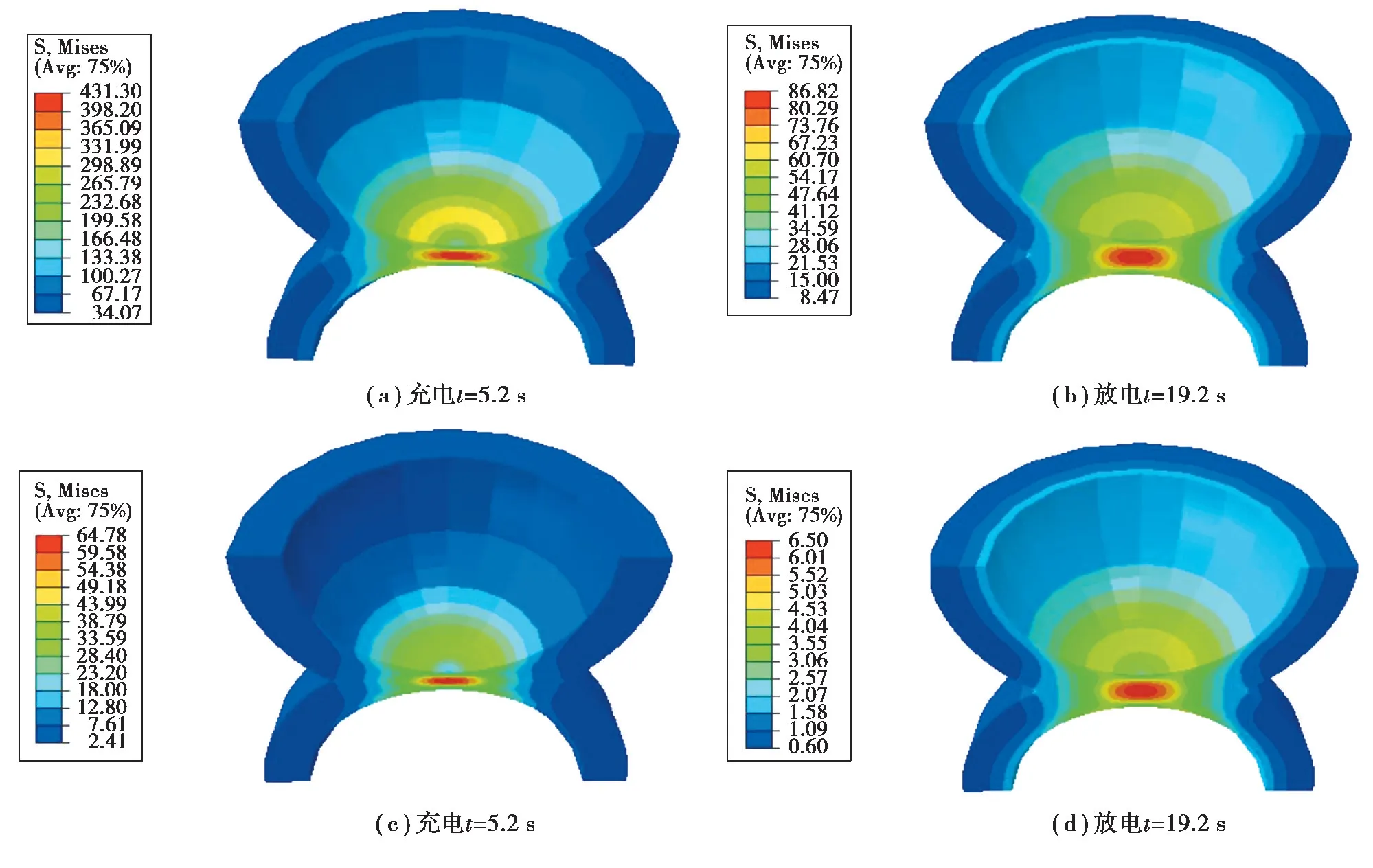
图8 充放电循环过程硅颗粒与粘结层受挤压的应力云图,电流密度8.37×10-2 A/m2Fig.8 Stress nephogram of silicon particles and bonding layer squeezed during charge discharge cycle,current density 8.37×10-2 A/m2

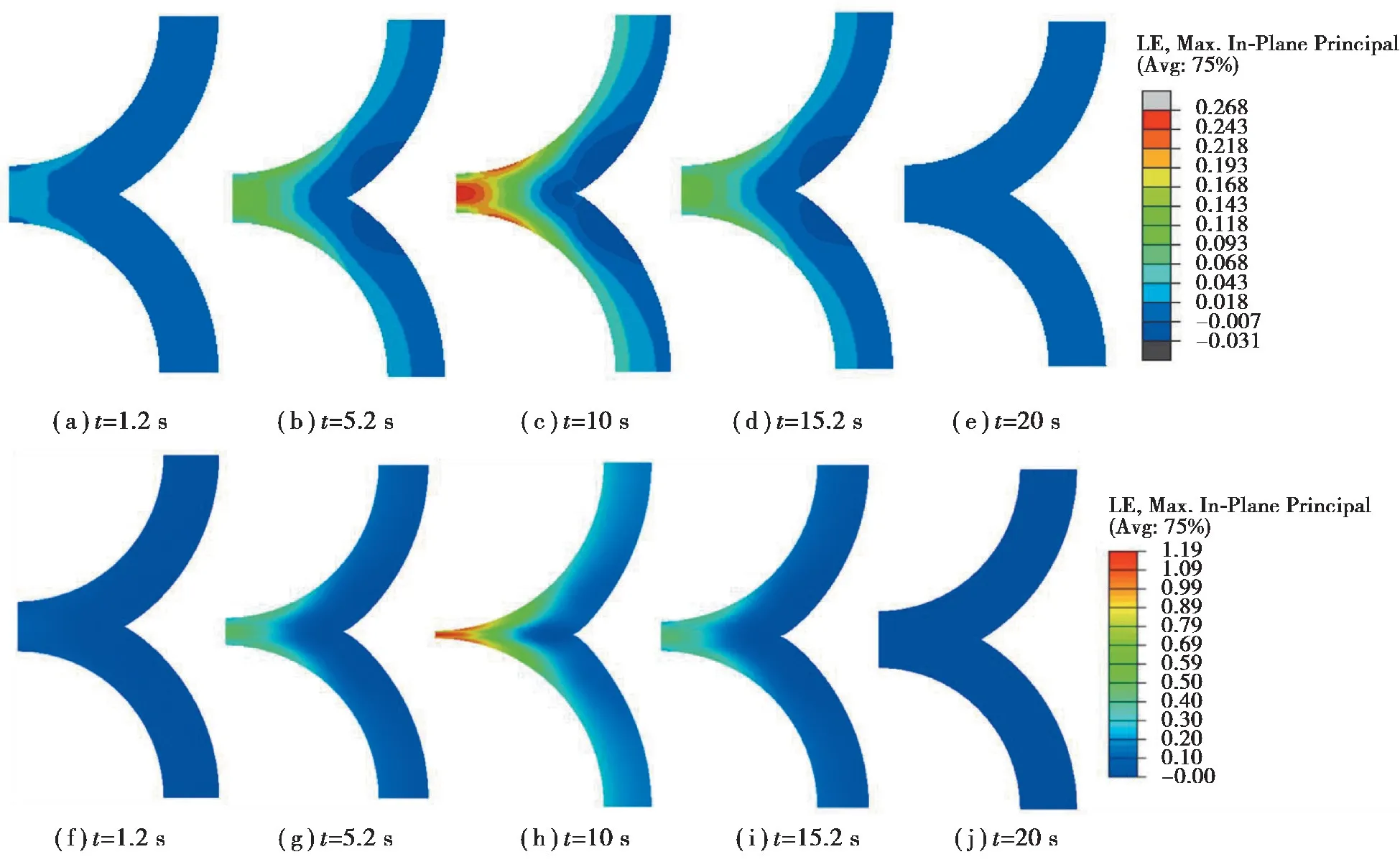
图9 充放电循环过程粘结剂层的应变演变云图Fig.9 Cloud diagram of strain evolution of binder layer during charge discharge cycle

从图9、图6的结果可以看出,充放电速率对应力、应变大小有影响。其它条件相同时,较快充电速率下的粘结剂应力和应变要大于充电速率慢的结果。

粘结剂含量是电池生产中1个重要参量,优化粘结剂含量会延长电池的使用年限。表2表示的是电流密度2.79×10-2A/m2下不同PVDF粘结剂层厚度40 nm、50 nm、60 nm、70 nm、80 nm 时,即不同粘结剂含量时粘结剂最大接触应力,最大的接触应力仍然发生在充放电循环的第一次充电过程中。可以看出,随着粘结剂层厚度的增加,粘结层界面的最大应力逐渐降低,但应力降低幅却逐渐减小。由于粘结剂为非活性材料,会降低电池的总容量,所以在不引起电池重量增加总容量减下的前提下,可适当增加粘结剂厚度来降低相应的应力,避免机械失效。

表2 粘结剂与颗粒界面层厚度与粘结剂最大接触应力Table 2 The thickness of interface layer between binder and particle and the maximum contact stress of binder

4 结论

针对锂电池复合负极极片中2个球形硅颗粒以及含有PDVF的粘结剂的两种情形,借助有限元温度 位移耦合模式,模拟了锂化硅颗粒及其与PVDF粘接层界面层在充电放电循环过程中的应力和变形,得到的结论如下:

硅颗粒锂化时主要的塑性变形发生在第1个充电放电循环过程中,这些形变引起了颗粒形状的不可逆变化,颗粒的永久形状变化会影响随后循环中的应力演化,硅颗粒体积膨胀过大会使粘结剂层产生较大的变形,易引起粘结剂层机械性能下降;充放电时2个硅颗粒的接触力峰值也发生在第1次的锂化/脱锂循环中,随后的循环中最大接触应力会下降,如果第1次的循环应力超过屈服应力,有可能导致颗粒破裂甚至电池失效。粘接层与颗粒间界面的最大应力变化与以上颗粒间接触应力变化类似,最大应力仍然发生在充放电循环的第1次充电过程中,随着粘结剂剂厚度的增加,粘结层界面的最大应力逐渐降低,第1次之后的循环中应力降低幅度会逐渐减小,因此可以在不引起电池重量增加总容量减下的前提下,适当增加粘接剂的厚度来降低相应的应力,避免锂电池机械失效。对于PVDF型粘结剂采用粘弹性模型更符合其实际的流变行为,这在较大行变下尤为如此。