两相低速非达西渗流模型及相对渗透率曲线求取方法

2022-04-01赵国忠董大鹏肖鲁川

油气地质与采收率 2022年2期

赵国忠，董大鹏，肖鲁川

（1.中国石油大庆油田有限责任公司勘探开发研究院，黑龙江大庆 163712；2.黑龙江省油层物理与渗流力学重点实验室，黑龙江大庆 163712）

在将达西定律应用于石油领域的过程中，两相相对渗透率曲线的获取是个重要环节。1959 年，JOHNSON 等建立了利用岩心一维非稳定流驱替数据求取两相相对渗透率曲线的方法［1-2］，已被石油行业标准所采用，适用于渗透率大于5 mD的岩样。

流体在特低渗透-致密油藏中的流动并不遵从达西定律［3-4］。闫庆来等依据低渗透岩心单相渗流实验结果推测，当压力梯度较小时渗流速度和压力梯度呈曲线关系［5］，通过将近似直线段延长交于压力梯度轴上而得到拟启动压力梯度，可以构建拟启动压力梯度模型［6］。然而，如何把单相流模型推广到多相流尚未形成广泛认同的做法，通常把单相流拟启动压力梯度直接用于多相流［7-10］，但这种做法缺乏实验和理论依据。开展两相非达西稳定流实验发现，两相流体整体的拟启动压力梯度并不等于单相时的值，且与含水率有关［11-13］。在此认识基础上建立了两相非达西渗流模型，认为两相情况下不同相的拟启动压力梯度相等且受控于空气渗透率和相分流率（或饱和度）［14］。目前为止，基于拟启动压力梯度依赖含水率的两相非达西渗流模型的相对渗透率曲线求取方法尚未严格建立起来［15-17］。

以两相低速非达西稳定流实验为依据，分析各相拟启动压力梯度相等假设的合理性，给出油水两相非达西渗流模型，并采用JBN方法的思路，从源头出发严格给出非达西情况下理论推导的条件，依据恒速法非稳定流驱替实验数据，建立求取两相低速非达西渗流相对渗透率曲线的方法。

1 油水两相低速非达西稳定流实验

采用稳态法，对大庆油田特低渗透岩心进行实验，研究油水两相的渗流特征。实验条件包括：实验温度为45 ℃；实验用油为模拟油，45 ℃时黏度为9.426 mPa·s；实验用水为质量分数为3%的KCl 溶液，45 ℃时黏度为0.639 mPa·s。

实验步骤如下：①对岩样依次进行抽真空饱和水、称重、测定孔隙体积、油驱造束缚水。②在束缚水饱和度下改变5 次不同的油相渗流速度，记录稳定时的压差，测定束缚水时油相拟启动压力梯度。③依次改变油水流速比为4∶1，1∶1，1∶4，在每一个油水流速比下改变5 次总的渗流速度，记录稳定时的压差，测定不同流速比下的油水拟启动压力梯度。④水驱至残余油，在残余油饱和度下改变5 次不同的水相渗流速度，记录稳定时的压差，测定残余油时水相拟启动压力梯度。

应用上述方法测试得到7块岩样不同含水率下的拟启动压力梯度，由岩样参数和实验结果（表1）可见，同一岩样在不同含水率下的拟启动压力梯度明显不同。所以两相情况下拟启动压力梯度不能直接使用单相的测试结果，必须考虑含水率的影响。随着含水率的增加，3号和4号岩样的拟启动压力梯度呈现先增后降的规律；而对于其他样品，虽然中间有个别波动，但总体也是呈现先增后降的变化趋势。

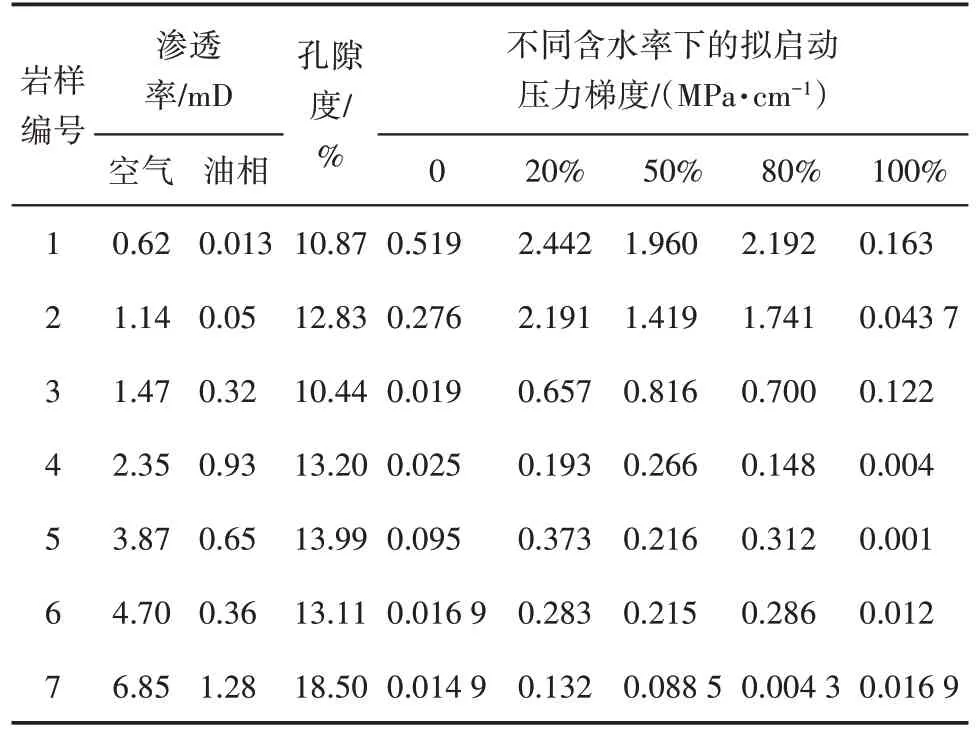
表1 不同含水率下的拟启动压力梯度Table1 Pseudo threshold pressure gradient at different water cut

应用表1 实验结果，建立最大拟启动压力梯度与空气渗透率的关系式，对每块岩样的拟启动压力梯度进行归一化处理，最终得到油水两相渗流时拟启动压力梯度的经验关系式为：

对于不同空气渗透率岩样，（1）式可用于计算油水两相流体在任意含水率下的拟启动压力梯度。此关系式并非普适的和唯一的，实验数据增多或岩石、流体类型改变，可重复以上步骤得到不同的近似解析关系式，且所得关系式只能用于油水两相低速非达西渗流模型之中。基于不同的渗流模型也会得到不同的关系式，但显然不可互用。曾有学者采用类似的实验方法得到两相启动压力梯度与含水饱和度的线性关系［18-19］，但所用岩样与本文实验不同，且如何从不同流速下两相稳定流实验结果得到两相启动压力梯度的方法不详。因其考虑的是二次非线性渗流，其应用也必须基于这种渗流模型而建立起来的渗流理论，但目前还未形成相应的完整理论体系。

2 油水两相低速非达西渗流模型

两相低速非达西稳定流动规律可描述为：两相不可压缩流体按一定比例通过岩石介质时总流速与压力梯度的关系，其表达式为：

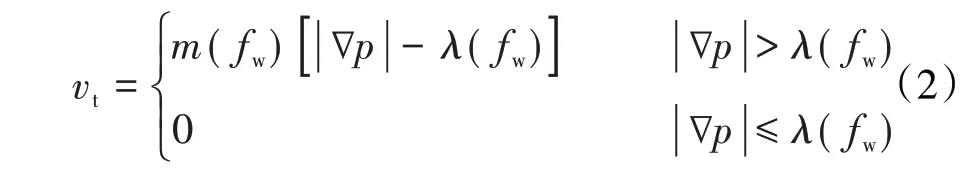
由于油、水按一定比例通过，等价于水按一定分流率通过，所以水相流速与压力梯度的关系为：

由（2）和（3）式知，2 条直线在 ||∇p轴上的截距，即拟启动压力梯度相等。类似的关系也适用于油相。这就是说，在一定的分流率下，各相的拟启动压力梯度都与两相总拟启动压力梯度相等，只是流动直线关系的斜率不同。

既然通过实验可以在一定的分流率条件下建立两相低速非达西稳定流，若把实验岩心看成油藏内的单元体，考虑实验持续时间相对油藏尺度下流体流动时间很短，可以认为油藏内任一点在一小段时间内的两相流动可以达到稳定。油藏内流体的非稳定流是由这样的无数稳定流构成的。其实达西条件下的两相流模型就是在此思想下建立的。因此，有理由假设两相低速非达西渗流各相的拟启动压力梯度相等，但其值与发生渗流位置的渗透率和当时的含水率有关。有学者在研究两相非线性渗流启动压力梯度时并未区分各相的启动压力梯度，已隐含了两相启动压力梯度相等的假设［18］。本文的研究使用的是相拟启动压力梯度这个参量，并假设其相等，这与文献［18］隐含假设是类似的，具有同样的道理。在该假设条件下，一维均质不考虑毛管压力情况下油水两相不互溶流体低速非达西渗流模型可表示为：

选取基准渗透率为束缚水时非达西流条件下的油相有效渗透率，等价于定义束缚水时油相相对渗透率为1，即：

多孔介质的渗透率是由达西定律定义的。须指出的是，在非达西模型下流动不再满足达西定律，渗透率的定义也该相应作出关联（3）或（4）式且形如（5）式的调整，才能构成完整理论体系，单相的情况也类似。这样定义的渗透率的量纲不变，且在忽略拟启动压力梯度时即为原达西流时的定义。

3 油水两相非达西渗流情况下JBN方法的适用条件

JBN 方法是建立在巴克利-列维里特前缘推进方程和威尔奇积分的基础之上，利用岩心一维非稳定流驱替数据获取两相相对渗透率曲线的方法［1］。由低速非达西渗流模型（4）式，可得出发生两相流动条件下含水率的表达式为：

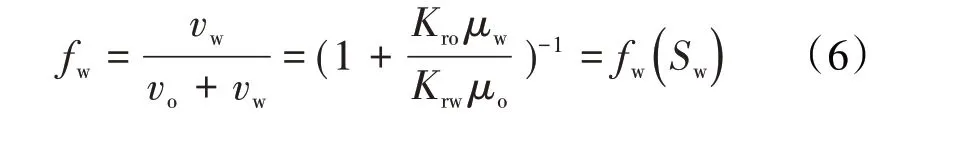
这表明非达西渗流情况下水相分流率仍然可表示为含水饱和度的函数，而黏度比只是参数，对于确定的流体其为常数。考虑不可压条件，由相连续性方程和饱和度约束方程仍然可以得到巴克利-列维里特前缘推进方程［20］：

（7）式表征了一维驱替过程中t时刻含水饱和度为Sw的推进规律。可将其用于横截面积为A、长度为L的一维均质岩心内，忽略毛管压力的油水两相不互溶流体低速非达西驱替实验。

忽略毛管压力是在特定条件下研究渗流单一影响因素的常用做法，也是建立基于非稳定流驱替实验数据求取相对渗透率曲线方法的前提条件。在使用驱替实验数据求取相对渗透率曲线的过程中，所涉及的出口端饱和度范围处于前缘饱和度和残余油时水相饱和度之间（这是非稳定流法求取相对渗透率曲线的局限性，达西流时也是如此），而入口端饱和度一直等于残余油时水相饱和度。日常由特低渗透岩样退汞曲线可转换得到油水两相毛管压力曲线，在此饱和度区间的毛管压力一般小于0.1 MPa，远低于特低渗透驱替实验的驱替压差，所以用于研究特低渗透岩心驱替的模型可忽略毛管压力。在应用本文方法所得相对渗透率曲线开展油藏工程研究或数值模拟计算时，可根据具体情况在模型中随时考虑毛管压力、重力等其他项的作用。

对（7）式积分可得t时刻含水饱和度为Sw的推进距离为：

由（8）式可得t时刻含水饱和度分布剖面，此剖面存在一个前缘饱和度Sw*，满足的条件是［20］：

而剖面上的饱和度范围为：

由于JBN方法求取的相对渗透率与含水饱和度的关系曲线是针对驱替实验出口端，由（10）式知，理论上讲JBN 方法只能得到前缘饱和度Sw*后的数据点。这一点是无论达西流与否都应该注意的适用范围，在此之外都没有理论依据，是不可信的。

由（8）式还可看出，在水驱前缘到达出口后的任意时刻，含水饱和度、含水率、含水率导数和坐标x具有一一对应（映射）关系，即它们之间都是两两单值函数关系。（8）式用于出口端可得［1］：

为后续推演方便，（8）式可进一步写成［1］：

基于低速非达西流模型即（4）式，由于以上诸条件的成立，威尔奇积分仍然成立，亦即存在岩心出口端含水饱和度与平均含水饱和度的关系为［2］：

平均含水饱和度可依据驱替数据确定：

而岩心出口端水相分流率或含水率可表示为：

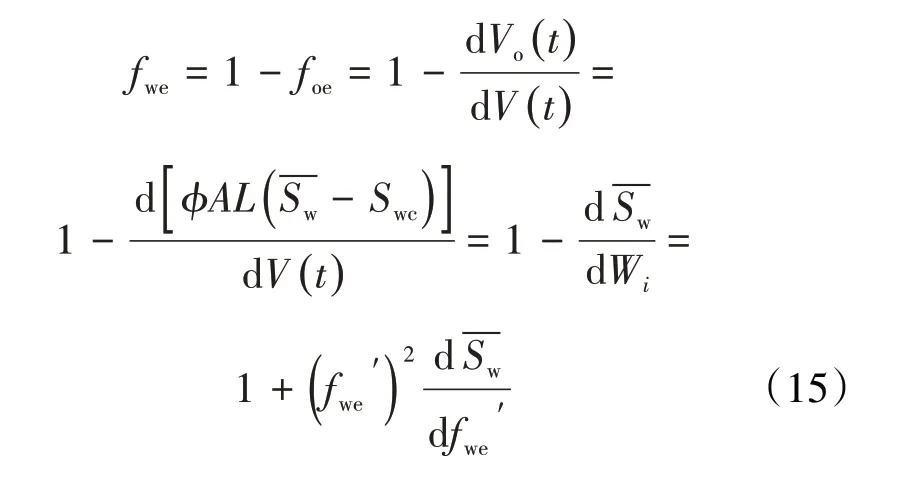
4 油水两相低速非达西流相对渗透率公式及应用实例

JBN 方法的关键是把流动方程运用于岩心驱替，通过积分得到岩心两端压差与出口端流动特征的关系，并由此定义一个可称为相对注入能力的时间变量，然后再对注入孔隙体积倍数的倒数，即求导，从而得到出口端相流度与相对注入能力的关系。在此基础上进行了公式推导及应用。

4.1 相对渗透率曲线计算公式

由（4）式可把非达西渗流模型在流动发生时刻t的水相方程（亦可选油相方程）表示为：

对（16）式沿岩心长度积分可得岩心两端压差为：

利用（12）式对（17）式换元可得：

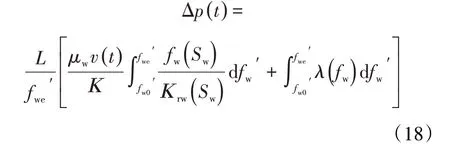
把（4）式用于驱替开始时的油相，再考虑（5）式，得：

若驱替实验采用恒速法，即v(t)=v(0)且为常数，则：

定义相对注入能力为：

则（18）式可表示为：

将（23）式代入（6）式，可求得：

4.2 相对渗透率曲线求取步骤

综合两相非达西渗流模型及相对渗透率计算公式，计算步骤可归纳为：①由（14）式利用驱替过程中的产油量数据计算并回归得到平均含水饱和度与注入孔隙体积倍数倒数的解析关系，即。②由（15）式求得出口端含水率与注入孔隙体积倍数倒数的解析关系，即。③由（20）式利用前期实验得到的拟启动压力梯度经验公式λ=λ()fw和驱替实验起始压差计算参考压力梯度λr。④由（21）式利用驱替过程中的压差数据计算并回归得到相对注入能力与注入孔隙体积倍数倒数的解析关系，即。⑤由（23）和（24）式求得出口端两相相对渗透率与注入孔隙体积倍数倒数的解析关系，即。⑥利用步骤①的结果由（13）式求得出口端含水饱和度与注入孔隙体积倍数倒数的解析关系，即。⑦依据步骤⑤和⑥得到的解析关系算出一系列注入孔隙体积倍数倒数对应的出口端含水饱和度和相对渗透率，作图得到两相相对渗透率曲线。

以上步骤与达西流情况的经典JBN 方法相比，步骤③是增加的，步骤④和⑤是不同的。

需要指出的是，不同于达西流的情况，如果未采用恒速法驱替实验，则不能由（22）式对fwe'微分而推导出（23）式。所以非达西流的相对渗透率求取须使用恒速法驱替实验数据。

4.3 相对渗透率曲线求取实例

以大庆油田某特低渗透岩心为例验证算法的可行性。实验基本参数包括：岩心长度为8.08 cm，直径为2.52 cm，孔隙体积为4.92 mL，孔隙度为12.20%，气测渗透率为1.131 mD，束缚水饱和度为42.07%，束缚水时达西流油相有效渗透率为0.047 6 mD，对应的束缚水时非达西流油相有效渗透率即本文所选基准渗透率为0.051 6 mD，油的黏度为5.20 mPa·s，水的黏度为0.57 mPa·s。所记录的实验数据见表2。

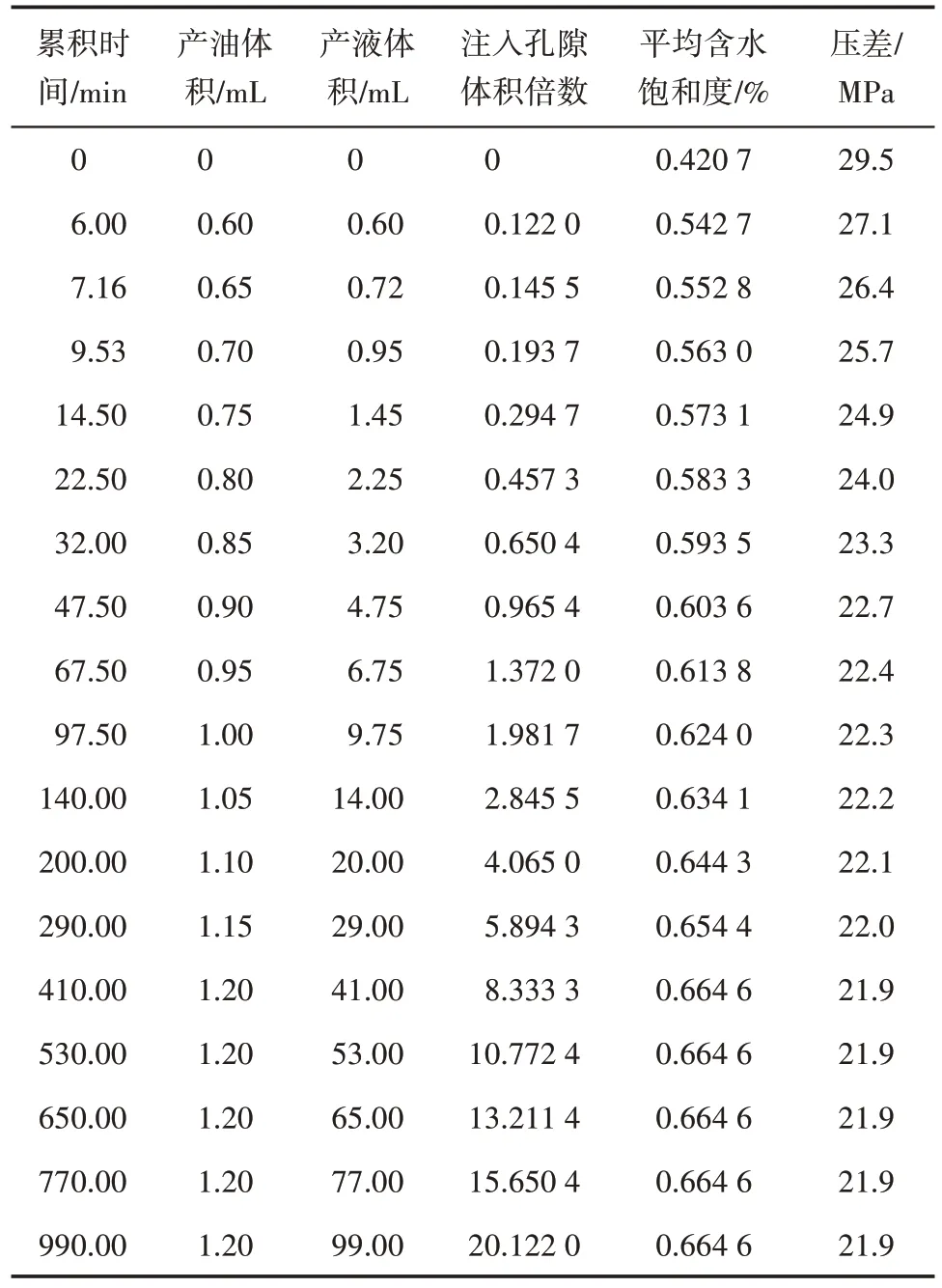
表2 大庆油田某特低渗透岩心实验数据Table2 Experimental data of a ultra-low permeability core from Daqing Oilfield

分别采用本文非达西流算法和达西流JBN 方法，计算得到相对渗透率曲线，结果如图1所示。在计算过程中，平均含水饱和度与注入孔隙体积倍数倒数的拟合函数关系为：

图1 非达西流与达西流相对渗透率曲线对比Fig.1 Comparison between relative permeability curves of non-Darcy flow and Darcy flow

其中，a1=0.592，a2=-0.005 55，a3=0.081 8，a4=1.5。

非达西流情况下，相对注入能力与注入孔隙体积倍数倒数的拟合函数关系为：

其中，b1=7.34，b2=0.36，b3=0.766，b4=-0.068 3。

对于达西流，考虑与非达西流情况的对比需要，基准渗透率仍然选择非达西流条件下的油相有效渗透率，则相对注入能力应为：

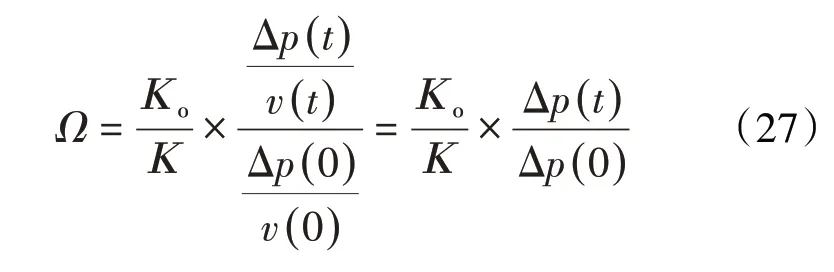
达西流时相对注入能力与注入孔隙体积倍数倒数的拟合函数关系式与非达西流情况相同，但对应的b1=0.684 5，b2=0.033 6，b3=0.766，b4=-0.006 37。

平均含水饱和度及相对注入能力与注入孔隙体积倍数倒数的拟合函数关系有个共同的特点，即当注入孔隙体积倍数倒数趋于0或注入孔隙体积倍数无穷大时，拟合函数的极限存在。这对相对渗透率端点值残余油饱和度及其对应的水相相对渗透率的确定提供了合理可行的办法，因为残余油饱和度是极限驱替条件下的含油饱和度［21-26］，实验达不到这个理想状态［27-28］。

计算结果表明，对于特低渗透岩心，考虑两相渗流拟启动压力梯度的影响后，油相和水相相对渗透率在等渗点之前都变高了；在等渗点之后油相近乎相同，而水相略微降低。这里应指出，非达西流相对渗透率曲线只可以用在基于非达西流模型的相关研究或应用中；而达西流相对渗透率曲线只可以用在基于达西流模型的相关研究或应用中。二者不应混淆。