电塑性效应中的磁场对金属流动应力的影响
2022-04-01刘武东李大龙王晨光宋建争
刘武东,李大龙,*,王晨光,宋建争
(1. 燕山大学 机械工程学院,河北 秦皇岛 066004;2. 燕山大学 环境与化学工程学院,河北 秦皇岛 066004)
0 引言
电塑性效应是指在金属塑性变形过程中向其塑性变形区通电导致的金属变形抗力急剧下降,塑性显著提高的现象。这种现象是前苏联学者Troitskii[1]于1963年首次在研究表面涂汞的锌单晶拉伸实验中发现,此后在金属加工过程中电塑性效应得到了广泛的应用。俄罗斯研究人员[2-3]通过电塑轧制生产了符合世界最高标准的钨片。唐国翌等研究了电塑性效应在轧制[4]和拉伸[5-6]中的应用,发现通过金属变形区的脉冲电流减小了拉伸和轧制所需的力,同时显著提高了塑性。电塑性效应在复合材料制备领域的应用也得到了广泛的研究,例如应用电塑性效应可以实现铜热浸镀铝界面扩散层厚度的定量化控制[7]。虽然目前金属的电塑性加工技术已取得较好的实验研究成果,但对电塑性效应的作用机理的研究一直处在探索之中,因此,开展电塑性效应的理论研究对于促进电流辅助制造工艺发展具有十分重要的意义[8]。
有三种主要理论试图解释金属中的电塑性效应:电子风效应、焦耳热效应和磁致塑性效应。在电子风效应理论中[9],当高密度脉冲电流流经金属材料时,材料内部将形成漂移电子,这种漂移电子作用在位错上时,会加快位错运动速率,打开位错间的缠结,促进位错脱离钉扎中心,并克服其滑移面上的障碍,从而导致流动应力的减少,延展性的增加,成形力的减少以及回弹的减少。焦耳热效应理论有两种形式:体积均匀焦耳热效应和非均匀微尺度焦耳热效应[10],体积均匀焦耳热效应理论认为由于材料内部电阻的存在,使得流过材料内部的电流与电阻相互作用而产生热量,这种热产生导致金属的热软化,从而提高成形性,降低流动应力、成形力和回弹。因此,体积均匀焦耳热理论的机理是体积均匀热软化,这与在加热炉中对金属进行热处理的机理相同。然而,为了解释超过等温加热所能达到的流动应力降低值,这一理论被扩展到微观尺度焦耳热效应。微观尺度焦耳热效应理论认为,由于金属的位错、晶格缺陷、层错、晶格错位和晶界而引起金属电阻率增加,将导致周围的局部区域非均匀性温度升高,超过了整体观察到的温度,并解释了同一区域内位错运动的改善,这种解释的机理本质仍然是热软化。磁塑性效应理论[11]认为含有顺磁性中心的位错芯和障碍物悬空键之间会形成自由基对,自由基对有单重态(singlet state, S态)和三线态(triplet state,T态)两种电子自旋状态,其中T态自由基对的结合能比S态自由基对高。通过金属的脉冲电流会产生磁场,磁场使得金属中的位错和障碍物形成的自由基对由S态跃迁到T态,间接提高了位错的能量,增大了位错从障碍物中脱钉的概率,从而提高了金属的塑性。
在上述三种主要的金属电塑性效应的机理解释中,电子风效应和焦耳热效应已经有大量的研究,而对于应用磁塑性效应解释金属的电塑性效应的研究很少有学者涉及。实际上早在1968年Hayashi就发现磁场可以提高金属的塑性,其在纯镍的拉伸过程中施加交变磁场发现了拉伸过程中的流动应力下降现象[12],并在1971年将这种由交变磁场引发的金属流动应力下降的现象命名为磁致塑性效应[13]。Strizhalo[14]在拉拔BrKh08Tsr青铜过程中施加脉冲磁场,Nembach[15]在拉拔纯铜过程中施加交变磁场,均观察到磁场使流动应力减小的现象,减小值随磁感应强度的增加而增大。
李桂荣[16]在脉冲磁场冲击铝合金的实验中发现,铝合金中的位错密度增加了16.3倍。Pamyatnykh[17]发现磁场可以促进铁磁性金属中的位错迁移,Bosin[18]发现磁场可以促进铜和铝中的位错运动。以上实验结果表明,磁场对金属中位错的运动有很大的影响。Molotskii[19-20]的自旋塑性理论认为,磁场改变了位错核和顺磁障碍物悬挂键形成的自由基对的自旋多重性,从而使脱钉变得更为可能,即磁塑性效应的本质是磁场促进位错从顺磁障碍物中脱钉。由位错核和障碍悬挂键形成的自由基对可能处于不同的自旋态,具有不同的结合能。通常强键结合只存在于S态,电子自旋状态是反平行的。在具有平行自旋的激发T态中,键结合能较弱。因此,S-T跃迁将导致键结合能的减弱和分子离解的概率增加。在没有磁场的情况下,S-T跃迁是严格禁止的。在磁场中,S-T跃迁成为可能。由于电子自旋和磁场的相互作用非常弱,只有在S态和T态的能量几乎一致的情况下,S-T跃迁才可能发生。这个条件只有在自由基对形成的非平衡态下才能满足。Golovin[21]已经证明在微观层面上,磁场通过促进位错-障碍体系中的S-T跃迁来影响金属的塑性。这导致T态自由基对数量增加,由于T态自由基对结合能低于S态,位错从障碍物中脱钉的可能性增大,金属的塑性增加。
从上述研究中可以发现磁场引发金属拉伸过程中流动应力减小的现象与电塑性效应有相似的地方,因而本文研究目的是从电流激发的磁致塑性效应的角度研究电塑性效应的微观机理,提供了一种计算电流诱导金属流动应力下降值的方法,促进电塑性效应理论的发展和电流辅助金属成形技术在加工工艺中的应用。
1 磁场下的位错动力学模型
由顺磁性障碍物钉扎的自由位错段的平均长度取决于磁场,即[11]
(1)
其中,B是磁感应强度,B0是位错有效脱钉的磁场特征值。
对于圆柱形试样,施加电流产生的磁感应强度为
(2)
其中,J是电流密度,μ是材料的磁导率,r是试件半径。
将式(2)代入式(1)可得
(3)
对于给定的位错段长度L(J)移动Δr的距离,位错扫过的面积为L(J)Δr。这导致了激活化面积A*的增加,即
(4)
在已知临界应力和激活面积的情况下,假设应变速率恒定,利用式(4)可以求得电流作用下的应力降方程
(5)
其中,σ*是有效应力。
试件在拉伸过程中施加电流时,在外力作用下的流动应力为
(6)
其中,σ是拉伸应力。
式(6)是Molotskii[11]根据自旋电子学得到的电流作用下金属流动应力下降的表达式,但是由于在式(6)的推导过程中没有考虑能量的变化,其计算值与实验值有较大的差异。因此,本文基于Molotskii的磁塑性效应理论,从电流引起金属中位错的激活能变化和激活面积变化的角度,推导一种计算电流引起金属中流动应力下降值的方法。
根据Molotskii的磁致塑性效应理论,磁场使得金属中的自由基对由S态跃迁到T态,S-T跃迁增加了金属中T态的总体数量。T态位错与顺磁中心之间的结合能明显低于自由基对的S态。因此,当外加磁场时,位错获得的激活能[22]
(7)
其中,μB是玻尔磁子,Δg是自由基对状态的g因子之差。
在通电时间t内,通过障碍物的自由基对数为t/τ0,位错获得的能量为
(8)
其中,τ0是自由基对通过共振区域的平均时间。
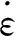
(9)
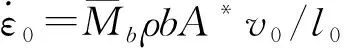
在金属拉伸过程中施加高密度脉冲电流会激发强磁场,位错从磁场中获得能量,使得位错自由能ΔH增大,此时,金属拉伸应变速率为
(10)
下标e表示电流脉冲相关的参数。将式(9)与式(10)两边同时取对数并相减
(11)
(12)
2 实验
2.1 金属本构方程的建立
为了研究电流对金属流动应力的影响,根据试验数据,通过多元回归研究了纯铜的流动应力、温度、应变速率和应变之间的关系,得到了纯铜的本构方程。铜丝的纯度为99.99%,直径为0.6 mm,长度为100 mm。在测试前,铜丝进行了退火,晶粒尺寸为25 μm。在高温万能拉伸试验机的帮助下,进行了应变速率范围(0.01、0.001和0.000 1 s-1)和温度范围(20、90和160 ℃)的单轴拉伸实验,结果如图1所示。
如图1所示,利用得到的实验数据,采用非线性最小二乘法回归优化方法确定了纯铜线的本构方程为
(13)

施加脉冲电流后铜的本构方程为
(14)

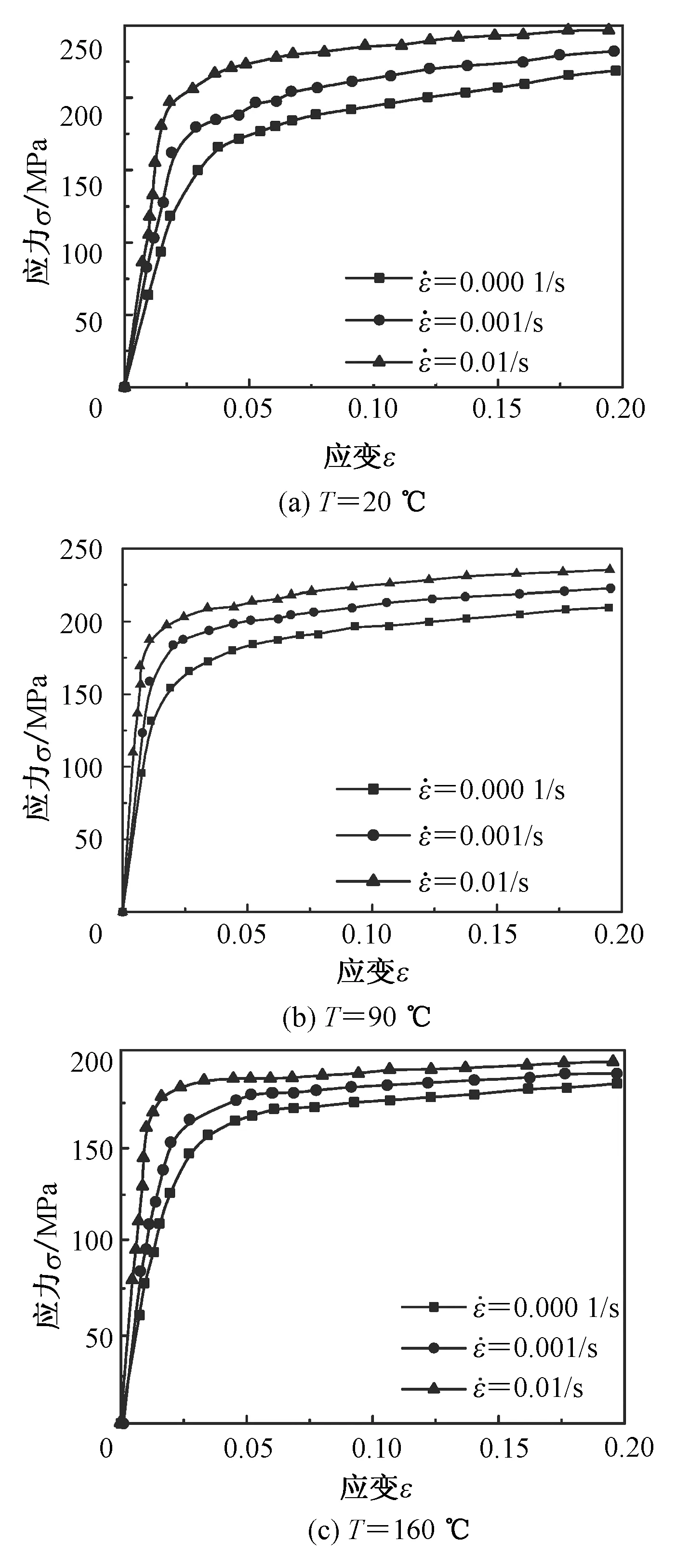
图1 纯铜流动应力-应变曲线Fig.1 The flow stress-strain curves of pure copper
电塑性效应必然伴随着电热效应,金属温度的升高也会导致金属流动应力的下降。因而在考虑电热作用下金属铜的流动应力和电流之间的函数关系为
(15)
2.2 电塑性拉伸实验
在美国Instron公司生产的型号为5848微力材料拉伸试验机上进行了电塑性拉伸试验,该拉伸机集成了闭环控制系统和数据采集电子系统。由电流脉冲引起的流动应力的稳定下降由计算机记录下来。由于试验机的惯性,单个电流脉冲后的负载降无法测量。因此,首先在1×10 s-1的标称应变速率下对试样进行塑性变形,达到13%的应变水平,然后施加40个连续的电流脉冲,相同的脉冲宽度为60 μs,相同的电流频率为8 Hz通过试样,产生应力降。在不同电流密度条件下对10组实验数据进行评估。电塑性拉伸实验装置示意图如图2所示,图3是铜丝流动应力随脉冲电流变化图。
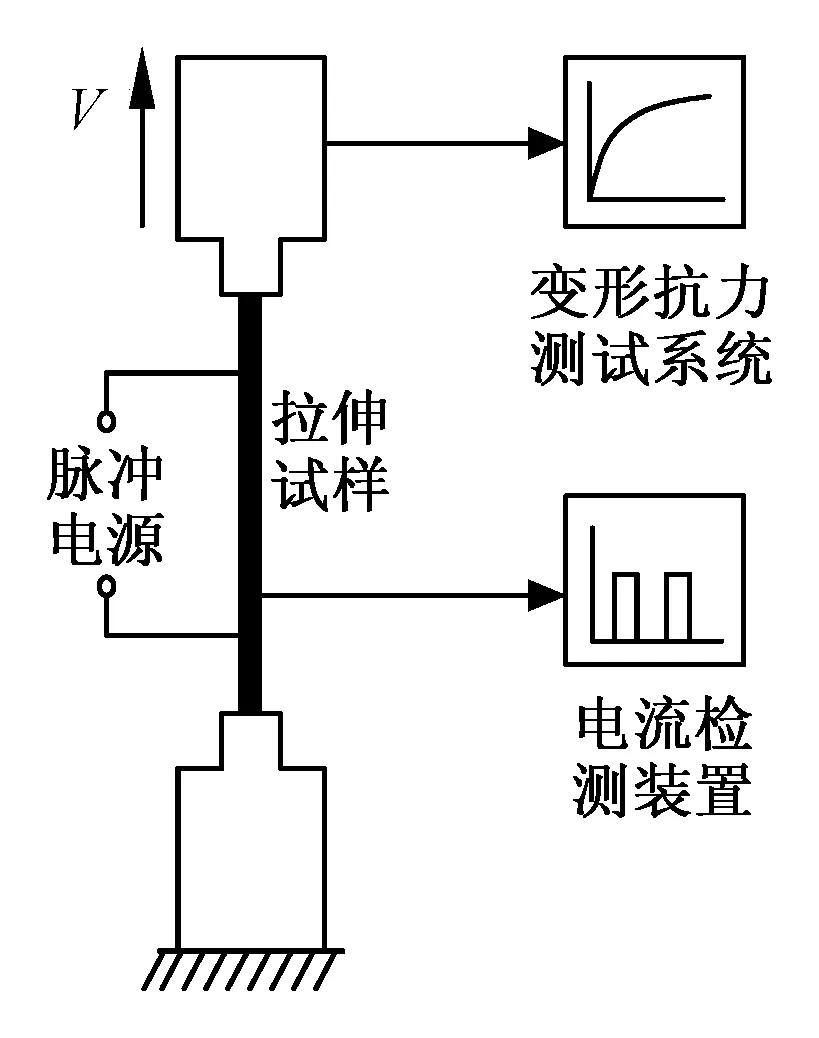
图2 实验系统示意图Fig.2 Configuration of the experiment system
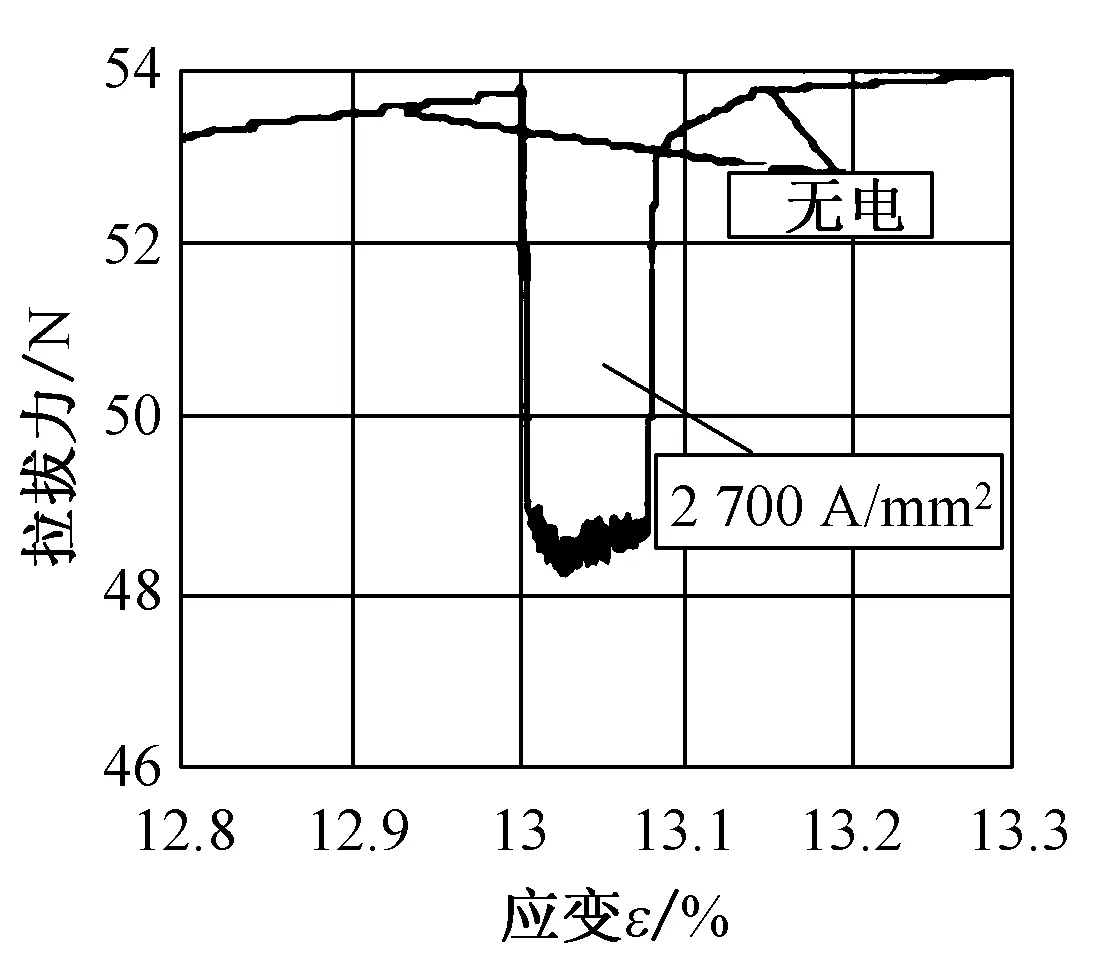
图3 铜丝拉伸力随脉冲电流作用的变化情况Fig.3 Diagram of the tensile force variations for copper wire with current pulses
在本文的试验条件下,其他电塑性二次效应(如集肤挤压)要小得多。因此,电流脉冲引起的流动应力下降是纯电塑性效应和电热效应共同作用的结果。
2.3 电热仿真实验
为了排除电热效应对金属拉伸应力试验值的影响,本文采用ANSYS有限元软件的热-电耦合分析模块对拉伸试样进行了电热效应模拟,得出了对流换热条件下的丝材温度升高量,模拟结果中包含了空气自然对流散热因素对试样温升的影响。当金属塑性变形达到13%的应变水平时电流对金属温度的影响如图4所示。将模拟的电热结果代入到式(13)中,可得出电热对金属拉伸应力的影响值。
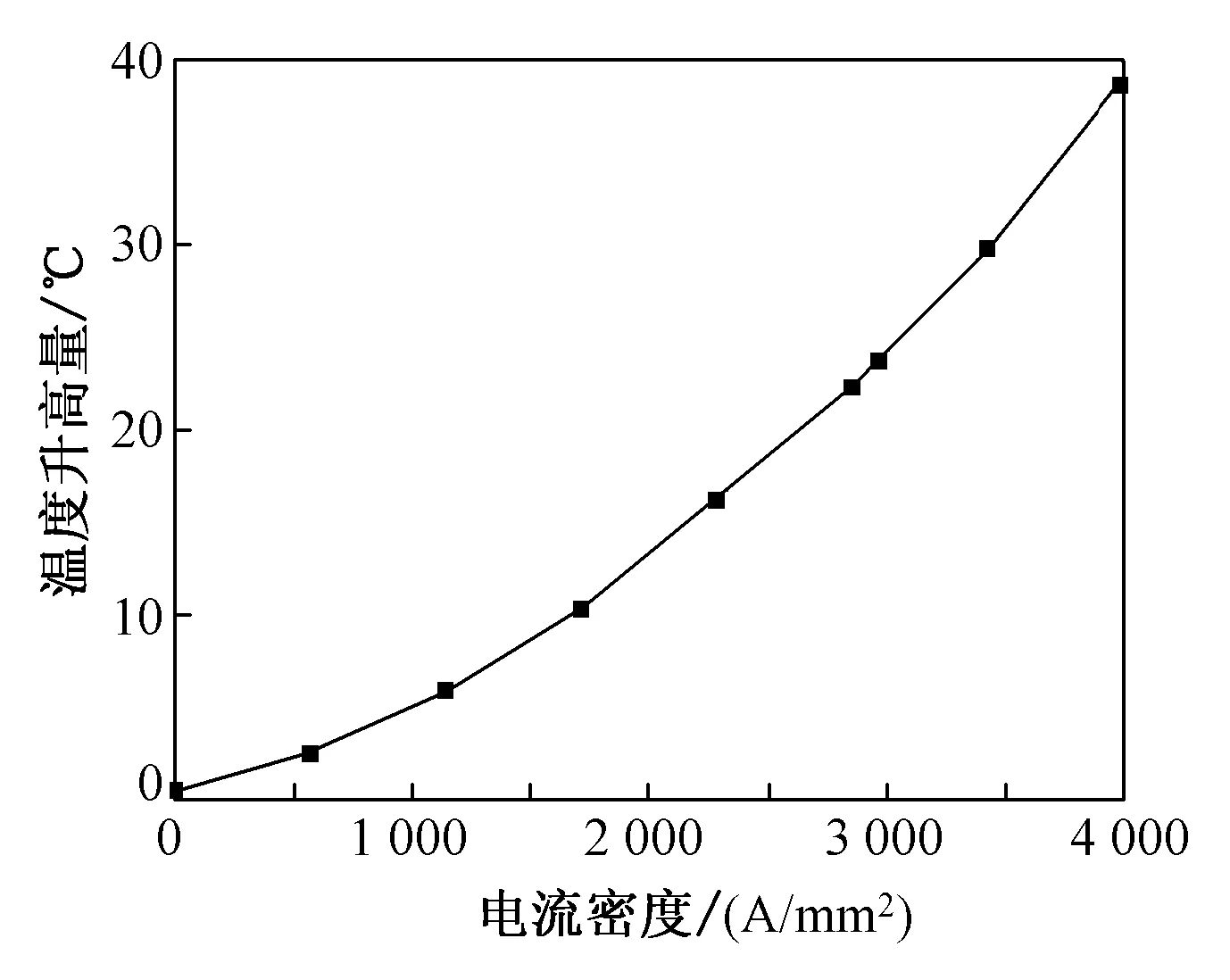
图4 试件温升随电流密度变化曲线图Fig.4 Relationship of increased temperature of specimen versus current density
3 实验结果分析和讨论
3.1 实验结果分析
根据式(13)和图4中的数据,计算出电热过程产生的流动应力的降低值,然后从实验值中减去得到纯电塑性效应对金属流动应力的影响如图5所示,图5中实验值表示微力材料试验机上显示的值。为通常金属铜的有效应力为实际拉伸应力的0.16倍,即σ*≈0.16σ。代入到式(6)中,其结果如图4中的σFe1所示。对于金属铜[19],Δg≈103,τ0≈10-7s,μ=1.257×10-6N/A,J0≈3 300A/mm2。将上述数据代入式(15)和式(12)中,由磁致塑性效应引起的流动应力减小值如图5中的σFe2所示。
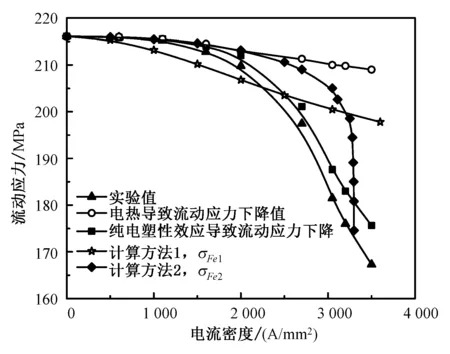
图5 流动应力的减小与电流密度的关系Fig.5 Relationship of decreasing amount of flow stress versus current density
3.2 实验结果讨论
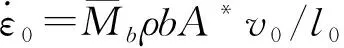
Conrad等[23]研究了单个高密度电流脉冲对金属流动应力的影响,他们利用理论推导和经验数据计算了施加脉冲电流时金属流动应力的减少量。本文提出的电塑性效应热激活观点与Conrad理论相吻合。在公式推导过程中,Conrad推导分析了漂移电子除了施加电子风外,如何影响位错热激活运动的其他参数,而本文根据磁致塑性效应理论计算了位错自由能的变化和激活面积的变化,得出了电塑性成形过程中流动应力的解析表达式。
最后从图5的实验和计算结果可以看到,当电流密度超过2 000 A/mm2时,理论计算结果和实验结果相差较大,出现这种现象的原因为本文从电流激发了磁场从而引发金属流动应力下降的角度出发,在结合磁塑性理论和热激活理论推导了计算方法2的表达式,在推导过程中并没有考虑电子风力的影响,大量的研究显示电子风力也会对金属纯电塑性效应产生较大的影响[9],电流密度越大电子风力的影响也越强,因而会出现当电流密度超过2 000 A/mm2时,计算方法2与实验值相差较大的现象。
4 结论
本文将位错滑移热活化理论与磁塑性效应理论相结合,研究了纯铜电塑性拉伸过程中,电流产生的磁场对金属流动应力的影响,得到了电流作用下金属拉伸应变速率与电流密度的函数关系,并将其代入到铜常规拉伸的本构方程中,计算得出了电塑性拉伸过程中铜丝的流动应力值。在电流密度0~2 000 A/mm2范围内,流动应力的计算结果与实验值有很好的吻合性,当电流密度超过2 000 A/mm2时,流动应力的理论计算结果和实验结果相差较大,产生这种现象的可能的原因为公式推导过程只考虑了磁场对金属塑性的影响,没有考虑电子风力对金属流动应力的影响所造成的。当电流密度增大到一定程度电子风力对流动应力的影响会更加明显,因此在将来的研究中需进一步考虑电流引起的电子风力和磁塑性效应的共同作用对电塑性效应的影响,用以提高电塑性效应的理论研究的准确性和全面性,为电流辅助金属塑性成形工艺提供理论依据。
