再入覆盖区域面积计算的一种球面矢量方法

淡 鹏，石 峰，王 丹，王 奥

(1 宇航动力学国家重点实验室，西安 710043；2 西安卫星测控中心，西安 710043)

0 引言

航天器升力式再入返回地球过程中，其制导和控制能力受到动力学系统的强扰动性、大气模型参数不确定性等因素制约，因而再入滑翔技术已经开始在一些航天器返回过程中进行应用，这使得此类航天器能够到达的地表位置区域呈现出较大的范围。将航天器再入过程能够到达的着陆或交班区域范围称作再入覆盖区域。

随着再入过程位置速度的变化，再入覆盖区域也在不断的变化中。为了评估实际飞行能力或必要时对航天器进行安控操作，常常需要计算再入覆盖区域的面积，以及该区域进入某个指定区域内的面积。

航天器再入覆盖区域一般可用一系列点围成的不规则的多边形来进行区域边界描述，这样覆盖区面积实际上就转化为这一多边形区域面积。而覆盖区进入指定区域内部分面积可转化为两个不规则多边形相交部分的面积计算。张海涛等提出了一种不规则区域面积四等分割计算法，通过逐次将目标区域所在的矩形四等分割，直到满足精度阈值要求为止，将区域内所有有效值相加得出区域总面积。葛伟华等提出了一种基于边界跟踪的区域面积计算方法，根据图像边界跟踪时下一次和上一次跟踪方向，确定图像左右边界，利用边界像素的横坐标进行加权求和计算，得到图像区域面积。但这些方法主要针对平面图形，应用到球面上时还需要一些改进。

而对于相交区域面积计算问题，魏许青利用Weiler-Atherton多边形裁剪算法实现了平面多边形的交集计算,但其也主要针对平面多边形。

对于球面上的计算问题，施一民等给出了一种用三顶点测地坐标计算椭球面上三角形面积方法来计算凸多边形面积；齐澄宇等提出了一种基于地球网格剖分的区域面积计算方法；刘洋等提出了一种基于抛物线拟合的椭球面区域面积计算方法。

文中从航天器再入覆盖区域面积及进入特定区域部分面积计算的实际情况出发，基于一般矢量运算及面积矢量概念，结合球面三角形运算法则，实现了一种再入覆盖区面积及相交面积的计算方法。

1 覆盖区面积计算

1.1 面积计算方法

以逆时针顺序排列的一系列经纬度点来表示再入覆盖区的边界。考虑到飞行器高度较高时，再入覆盖区范围可能较大，因而使用传统的平面上区域面积计算方法将会存在较大偏差，故计算时需要考虑球面形状。

在计算球面多边形面积时，一种有效的方法就是将多边形分割成多个三角形，然后利用球面三角形面积公式进行计算。

设如图1所示的球面上,,三个点的经纬度坐标分别为[,]、[,]、[,]，地球半径为，边,,所对应的地心张角分别为,,。

图1 球面三角形示意图

由球面上两点距离公式可计算出：

(1)

再由球面三角余弦公式可计算出点处三角形内角为:

=arccos[(cos-coscos)(sinsin)]

(2)

同样可计算出点,处的三角形内角,。

则由球面三角形面积公式可得到三角形的面积为:

=(++-π)

(3)

将表示再入覆盖区的多边形分割成多个三角形，即可通过累加这些三角形面积得到可达区面积。但是由于再入覆盖区是不规则的，且常常是凹多边形，直接分割算法有时不便使用。

为此，借鉴面积矢量的定义，在三角形分割及面积计算时，将计算的面积定义为有向面积。

具体计算方法为:对如图2所示的由个点组成的球面多边形再入覆盖区，将逆时针顺序排列的各个顶点依次标记为,,,…,-1，以第0个点为基准点(为便于后续表达，同时将点标记为)，逆时针方向遍历其它点，每两个相邻的点与基准点组成三角形，计算其有向面积，并进行累加。

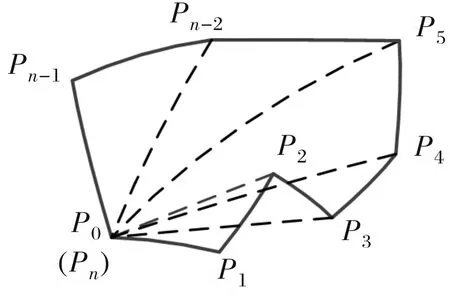
图2 球面多边形三角划分示意图

设,,组成的球面三角的有向面积为;,,球面三角的有向面积为，依次类推，则整个球面多边形面积为:

=|++…+0-(-2)-(-1)|

(4)

1.2 球面上面积正负判断

使用式(4)计算时的重要一点是进行面积的正负符号判断。根据有向面积的定义，当三角形第三个点出现在逆时针方向时为正，反之为负。

为了简化顺逆的判断，一种思路是采用平面图上矢量运算的判断方法。以经度方向为方向，纬度方向为方向，建立各点经纬度坐标的平面图。对平面图中某个三角形Δ+1，则由矢量运算定律，在平面图上，若点到矢量0叉乘点到+1的矢量0(+1)，所得结果大于0，则由右手法则，点+1在矢量0的逆时针方向，反之在其顺时针方向。这样即可判断出各三角形的正负号。

但该方法对球面三角形有误判的可能，为此改用球面上矢量关系运算。

如图1所示，对点序列,,，判断点在点序列,逆时针方向方法为:首先计算出逆时针遍历的前两点与球心所在平面的法向量,然后计算向量在该法向量上投影值,若其大于0，则在逆时针方向；若小于0，则在顺时针方向，等于0时不构成球面三角形。

2 相交区域面积计算

对再入可达区评估计算中，需要计算可达区与一个指定的目标区域相交部分的面积，也就是两个球面多边形相交部分的面积计算。

2.1 相交部分计算

对球面上相交部分的计算，最简单的是当两个球面多边形区域都是三角形的情况。

如图3所示为两个球面三角形，计算其相交区域，多边形边界点集可采用切割算法。

具体实现方法为：以逆时针点序遍历第一个三角形每两个相邻顶点构成的连线，循环判断第二个多边形各个顶点位置，若该顶点在连线逆时针方向，则保留；若在顺时针方向，则舍弃；若一个顶点与上一个顶点在不同方向，则计算当前连线与这两个顶点连线的交点，保留该交点；对第二个多边形遍历完后，即可得到对用当前连线切割第二个多边形一次后的剩余多边形包络点集。循环进行此切割,即可最终得到两个三角形相交部分包络点集。

图3 三角形相交部分计算示意图

切割算法也可扩充到两个凸多边形的情况，但是当多边形为凹多边形时就不再适用。为此，继续使用有向面积算法，先将两个多边形以各自的一个基准点进行三角划分(如图4所示)；然后遍历第一个多边形各三角面片，分别计算其与第二个多边形各三角面片的相交部分的面积，然后累加这些面积即可得到两个多边形相交部分面积。

图4 球面多边形相交部分计算示意图

具体地，对第一个多边形中一个三角面片Δ+1，首先判定该面片的正负号(符号记作Sign)，若为负值，则交换与+1坐标，形成临时三角形1；若为非负数，则直接作为临时三角形1。同样对第二个多边形中一个三角面片Δ+1(其符号记为Sign)，使用上述方法形成第二个临时三角形2。然后计算临时三角形1与2相交部分面积(记作，为正数)，则两个三角面片相交部分有向面积为：

(Δ+1,Δ+1)=Sign·Sign·

(5)

进而得到两个多边形相交部分面积为：

(6)

式中:,分别为,两个多边形顶点数。

2.2 两条弧线交点计算

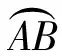
设球面上一点的经纬度分别为,，则其在地球固连系下的直角坐标为:

·[coscos,sincos,sin]

(7)

式中为地球半径。

则由点，，及球心可确定一个平面，设该平面方程为:

++=0

(8)

系数,,计算方法参见解析几何相关内容，此处不再赘述。

由,及球心形成的平面方程为：

++=0

(9)

同样，对半径为的球体，有

++=

(10)

联立式(7)～式(10)可计算出交点的直角坐标，进而计算出其经纬度值。

但该方法编程实现较为复杂，此处仍采用矢量运算的方法。

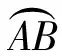
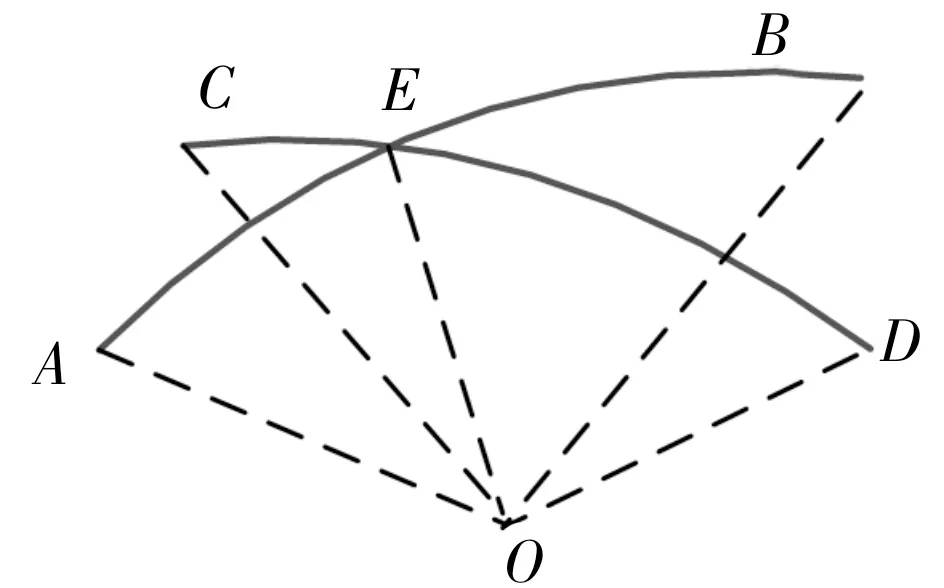
图5 两条弧线交点计算示意图

此方法解出的点有两个解。解选择方法为：分别计算出两个解离，,,四个点的球面距离和，取距离和最小的点作为所选择的点。

2.3 仅一个相交区域时的简化处理

上面的相交区域计算方法实现较为复杂。当覆盖区与目标区域的相交部分仅为一个封闭区域，不可能有两个或多个不相连接的封闭区域时，可以进一步作简化处理。

如图6所示，两个多边形只有一块相交区域时，简化处理方法为：逆时针顺序遍历第一个多边形各边，若判断出该边与第二个多边形某边有交点时，记录下该交点，将其作为两个多边形交集的第一个点；然后继续遍历第一个多边形的下一个边，若与第二个没交点，将该边第一个顶点加入交集定点序列；若有交点，计算出交点加入交集序列；然后将第二个多边形该交点后的所有顶点加入交集序列，直到到达第一个交点处时结束，将多边形顶点序列作首尾相接处理，这样即可得到相交部分多边形顶点序列。进而通过此多边形面积计算即可得到交集部分面积。

3 算法验证

为了验证该球面上覆盖区面积算法的可行性，以多边形面积计算中常用的网格分割算法为比较对象，将球面多边形在经度、纬度方向进行等间隔分割并计算各网格的面积，进而累加出可达区及其与目标区域交集部分面积，然后与文中方法进行比较。

考虑到网格分割算法在边界处可能存在面积多算的问题，故对结果的比较只要求近似即可。

计算时为了简化处理，将地球半径设置为1。对比如表1所示。由表中数据可见，两种算法计算结果较为接近。

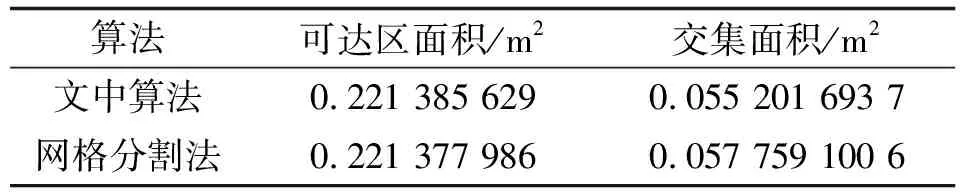
表1 计算结果对比(球半径设为1)

4 结论

通过将平面上多边形计算常用的有向面积概念扩充到球面上，给出了一种再入覆盖区面积及其与目标区域交集部分面积的计算方法，计算结果表明该方法是可行的。

需要注意的是，因该算法使用了球面三角形面积公式，而球面三角形的边是通过球心的大圆上一段弧线，但通过两点的弧线可以存在很多条，因而使用时多边形顶点个数不能过少，应能控制各边走势为宜。同时为了提高精度，应适当增加控制顶点的数量及减小间隔。

应该看到，此算法实现还是稍显复杂，下一步将重点在算法的简化处理及性能改进上进行研究。