气动加热环境下壁面热响应的快速分析方法

洪 元，刘亮堂，杨立明，祝成民

(1 航天恒星科技有限公司，北京 100086；2 北京航空航天大学宇航学院，北京 102206)

0 引言

飞行器的热防护设计需要计算壳体的温度分布。计算的关键是得到准确的输入热流等边界条件信息。对气动加热的分析方法主要包括经验公式、数值分析和风洞实验。风洞实验得到的数据最准确，但实验费用昂贵，且受条件限制，实验的相似准则参数在很多情况下达不到实际飞行时的参数值，只能在少数情况下使用。经验公式方法计算简单，但是适用范围窄。数值分析方法可以得到详细的热流分布数据，在通过实验校正的情况下也有较高的精度，是目前使用比较广泛的气动热分析方法。已有的研究结果表明，气动热计算会受到物体表面温度的影响，而物体表面温度是气动加热和物体内部传热与蓄热互相平衡的结果。所以只有将气动加热与被加热物体传热耦合计算才能保证计算结果与实际情况相符。但是，气动热数值分析计算量大、耗时长，造成耦合计算的代价太大，不适合工程设计。为了解决这个问题，研究人员提出了快速计算方法，但是这些方法还没有在飞行器热防护设计中实际应用，其有效与否仍需通过实践检验。如何在保证分析精度的基础上加快计算速度仍然是气动加热热防护设计中急需解决的问题。

文中借鉴经验公式方法的原理，提出了一种气动热与壁面传热的松耦合计算方法，该方法应用于气动加热热防护工程设计取得了较好的效果。

1 理论描述

1.1 物理模型

假设壳体为等厚度平板结构，内部热源为恒温热源，其外壁面承受均匀的气动加热，内壁面通过对流和辐射与内部热源进行热交换。由于壳体上下表面传热均匀，壳体内相同深度处的温度在任何时刻都相同，所以只需考虑热量沿深度方向的传递，壳体热响应可简化为一维非稳态问题，如图1所示。

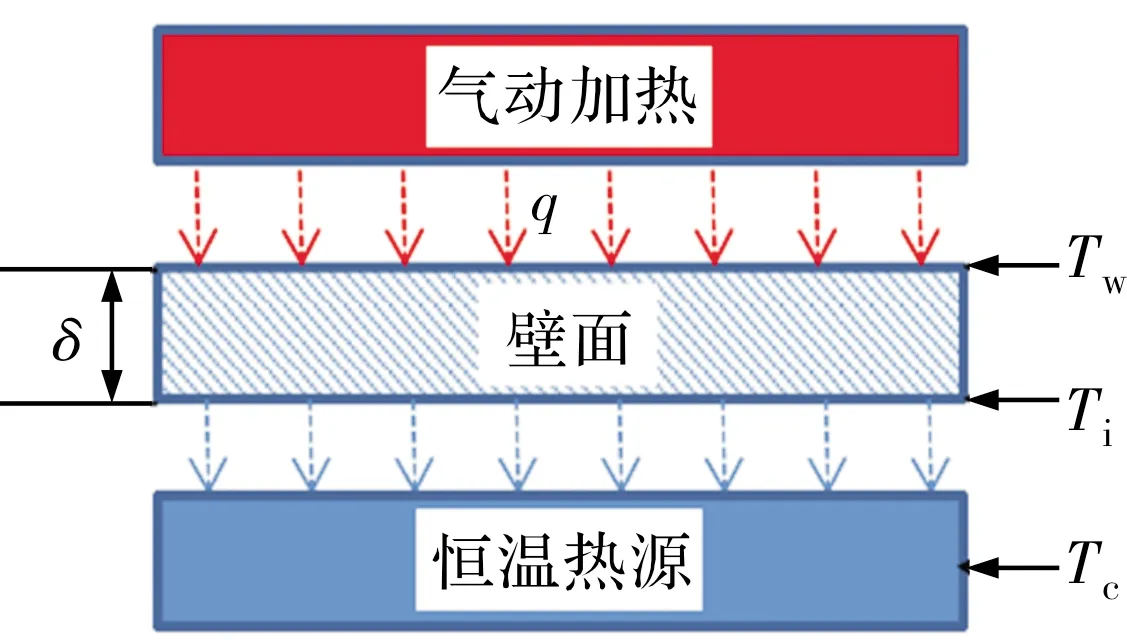
图1 物理模型示意图

1.2 气动加热计算模型

根据边界层传热有关理论，通过边界层对壁面的对流换热可表示为：

=(-)

(1)

式中:气体对壁面的热流密度;,为边界层外缘的气体密度和速度;为斯坦顿数;为恢复焓;为壁面处气体的焓。令=，则式(1)可简化为：

=(-)

(2)

由式(2)可以看出，气动加热中的对流换热计算可以归结为如何确定恢复焓和换热系数的问题。为了解决这一问题，需要使用数值分析方法求解气动热问题。首先设置气动热计算的壁面边界条件为绝热壁得到恢复焓；然后设置壁面为恒温边界得到参考温度下的壁面热流，将这两个计算得到的和代入式(2)可求得到换热系数值。在得到恢复焓和换热系数后，再计算壁面温度因内部传热而改变的最终情况。该热流作为壁面热传导方程的边界条件给出，从而实现气动热与物体内部传热的松耦合计算。

1.3 传热方程

根据上述物理模型假设，物体内部热传导控制方程为：

(3)

式中:为时间;为深度;(,)为物体内部深度为的点在时刻的温度;=()为热扩散系数;为物体的导热系数;为物体密度;为物体的比热容。

1.4 边界条件

边界条件包括外壁面边界和内壁面边界，具体如下：

1)外壁面边界条件

壳体外壁面承受气动加热的作用，考虑到辐射散热的影响，外壁面边界为：

(4)

式中:=，为空气定压比热容;为外表面辐射系数。

2)内壁面边界条件

壳体内壁面边界条件分为两种情况：一种内壁面与恒温热源直接接触，则有:

=，=

(5)

另一种内壁面与恒温热源通过对流和辐射进行换热，则有:

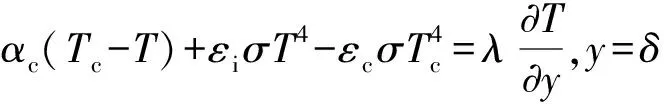
(6)

式中:为壳体厚度;为恒温热源;为内壁面与恒温热源的对流换热系数;为内表面辐射系数;为恒温源辐射系数。

2 数值计算

2.1 计算方法

热传导控制方程，即式(3)为二阶抛物型偏微分方程，可以采用经典的显式中心差分格式求解。

如图2所示，将由空间坐标和时间坐标构成的计算域划分为均匀网格。空间方向的网格间距为，时间方向上的网格间距为。图中圆点代表上一时间步的已知量，叉代表待求量。

图2 差分网格示意图

经典显式中心差分格式的计算公式为：

,+1=(-1,-2,++1,)+,

(7)

式中,=，称为网格比。根据偏微分方程数值稳定性分析，当≤12时，数值格式是稳定的。

2.2 边界条件处理

1)外壁面边界

对于外壁面边界条件，设：

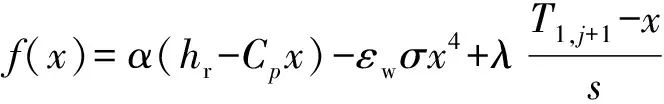
则根据式(4)有(0,+1)=0。采用牛顿迭代法求解该方程：

(8)

式中′(·)为(·)的导数。迭代过程中选择1,+1为初始条件。

2)内壁面边界

对于内壁面边界条件，设边界节点所对应=。如果内壁面直接与恒温热源接触，则有：

,+1=

(9)

如果内表面通过对流和辐射与恒温热源进行热交换，设：

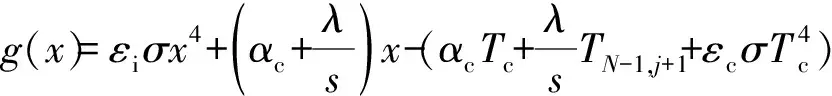
则根据式(6)有(,+1)=0。采用牛顿迭代法求解该方程：

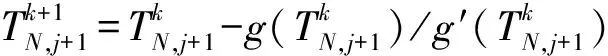
(10)

式中′(·)为(·)的导数。

3 计算结果及有效性分析

为验证文中分析方法的有效性，以型号1、型号2两种导弹的天线窗为例，选取其经过飞行验证的样本数据与文中计算结果进行对比分析。两导弹的天线窗均采用石英聚酰亚胺材料，其物性参数如表1所示。

表1 天线窗材料物性参数

3.1 案例1

型号1导弹天线窗厚度为5 mm，包含37 s、140 s、240 s三种飞行工况：

1)飞行工况1

飞行时间37 s，计算结果如图3所示。从图中可以看出，整个气动加热过程存在两个峰值，本模型计算结果与样本数据基本一致，二者最大偏差为24.5 ℃，其相对误差约为4.9%。

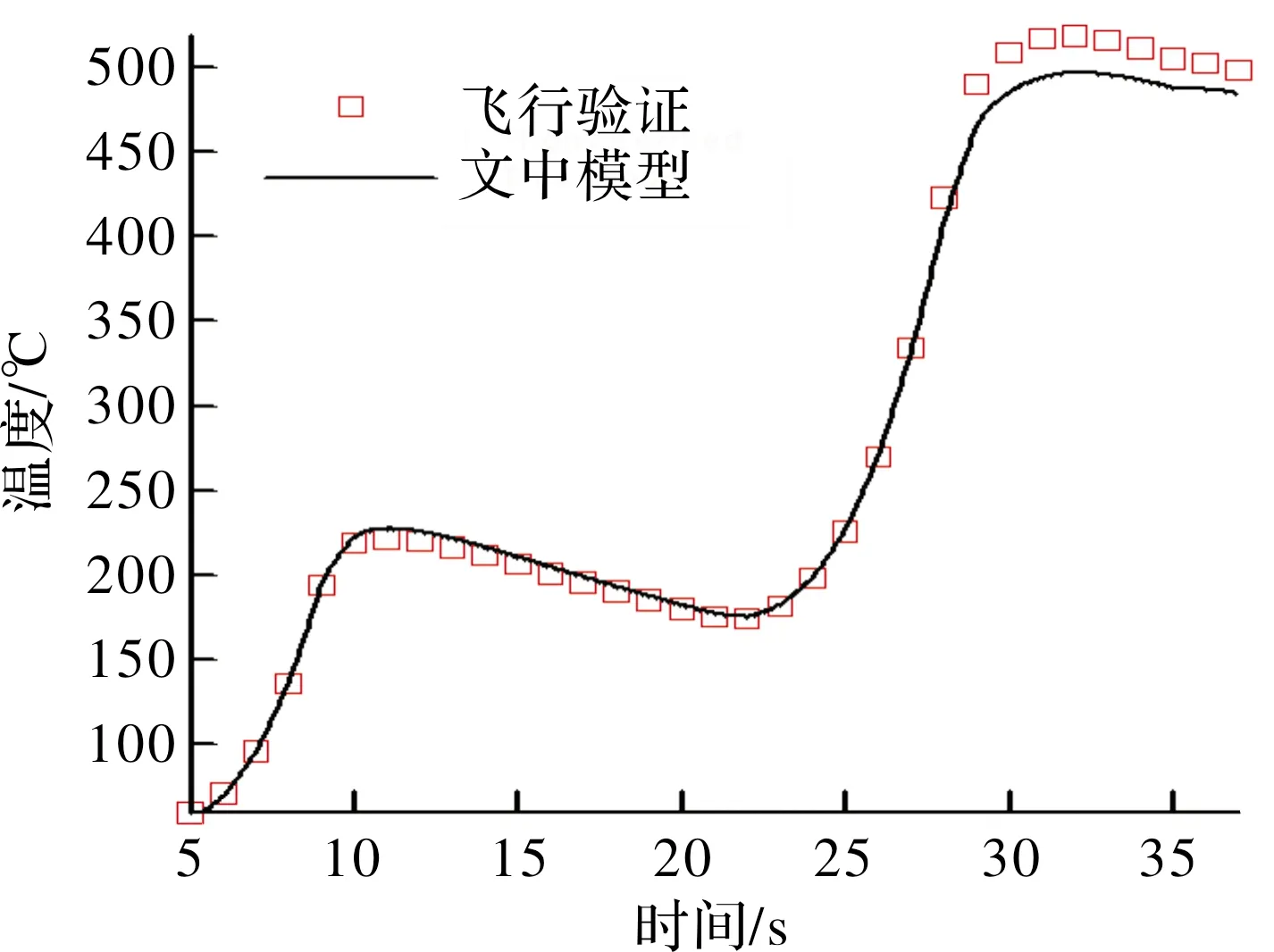
图3 型号1天线窗壁温计算结果对比图(飞行工况1)

2)飞行工况2

飞行时间140 s，计算结果如图4所示。从图中可以看出，整个气动加热过程存在3个峰值，本模型计算结果与样本数据基本一致，二者最大偏差为5 ℃，其相对误差约为2%。

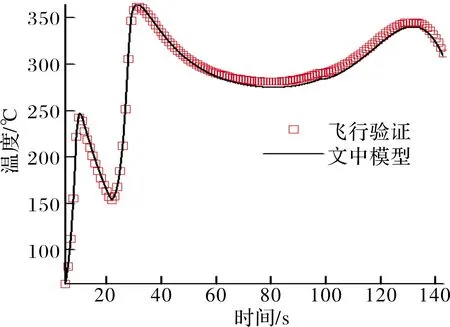
图4 型号1天线窗壁温计算结果对比图(飞行工况2)

3)飞行工况3

飞行时间240 s，计算结果如图5所示。从图中可以看出，整个气动加热过程存在两个峰值，本模型计算结果与样本数据基本一致，二者最大偏差为7 ℃，其相对误差约为3.3%。

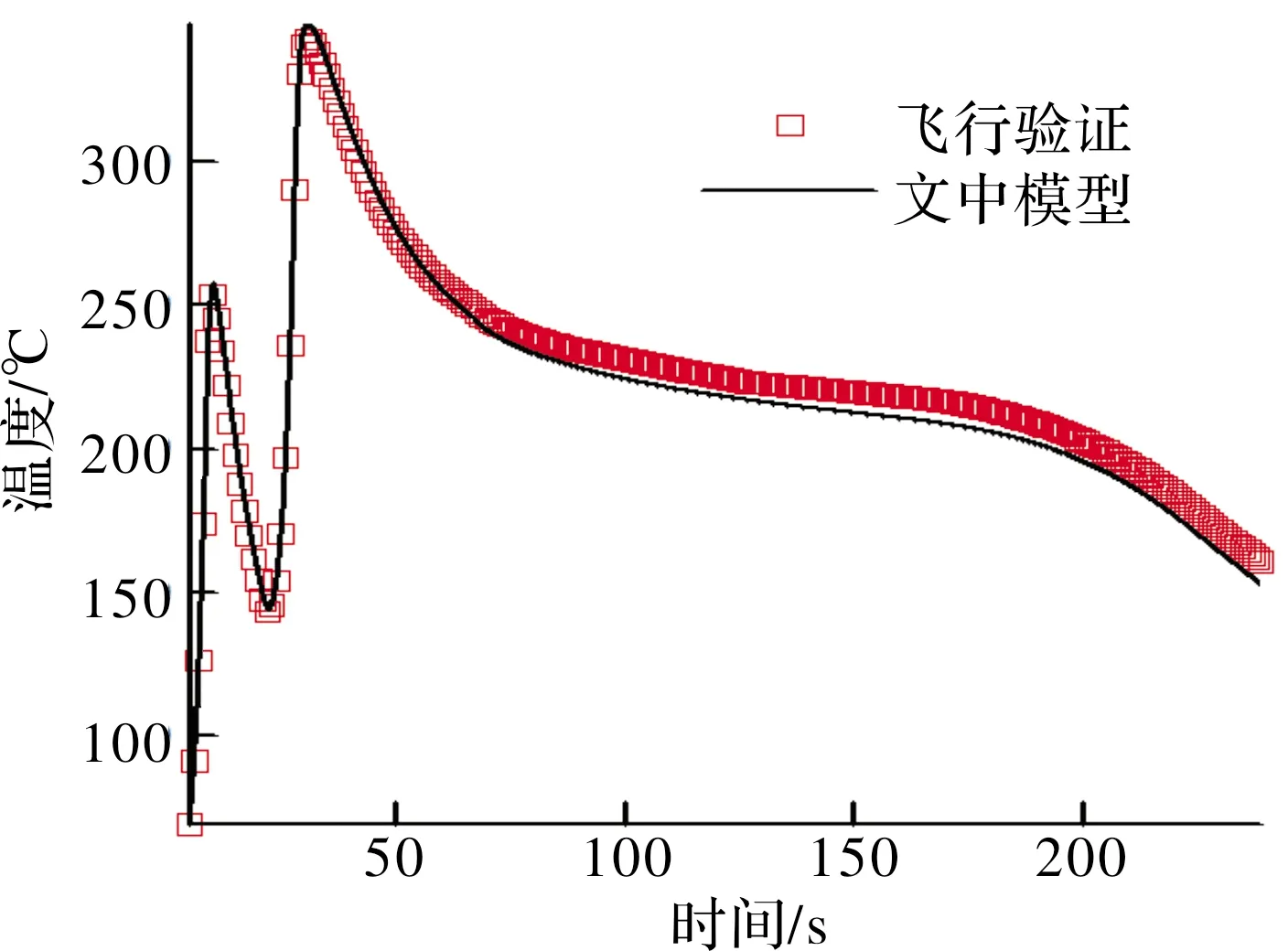
图5 型号1天线窗壁温计算结果对比图(飞行工况3)

3.2 案例2

导弹天线窗厚度为7 mm，其飞行时间为418 s，计算结果如图6所示。

从图中可以看出，整个气动加热过程存在3个峰值，本模型计算结果与样本数据基本一致，二者最大偏差为24 ℃，其相对误差约为5%。

图6 型号2天线窗壁温计算结果对比图

3.3 结果分析

通过对比可以看出，文中模型的计算结果与样本数据整体符合性较好，计算误差可控制在5%以内，满足工程设计的需求，证明了文中模型的正确性及工程应用的可行性。

此外，文中模型采用气动热与物体热传导的松耦合计算方式，其计算资源和计算时间主要集中在恢复焓和恒壁温热流的计算；传热计算基于一维传热模型完成，资源占比较小，计算时间一般不超过1 min。在气动热防护设计时，由于气动外形变化很小，工程上可假定恢复焓和恒壁温热流等气动热环境数据一定。在这种情况下，每次迭代设计采用文中模型可在几分钟内完成计算。相比于气动热与热传导的紧耦合计算模型，文中模型可将计算效率提高一个量级，非常适合气动热防护设计的工程应用。

4 结论

文中建立的松耦合计算方法可以正确评估气动加热对飞行器壳体等相关部件的热响应问题；使用恢复焓和传热系数解耦气动热与物体热传导计算的方法具有极高的计算效率，相比于传统紧耦合计算方法效率提高一个量级，满足气动热防护工程设计需求，并为高超声速飞行器的气动热防护优化设计提供技术支撑。