基于反正切函数的LMS自适应滤波算法及应用

张晓亚，刘建勋，倪元相，吴 亮，彭金奇

(1 广东工贸职业技术学院机电学院,广州 510510;2 东南大学机械工程学院，南京 211189; 3 广东理工学院科技处,广东 肇庆 526200)

0 引言

无线电引信是依靠无线电波来获取目标物信息，进而获得准确的引爆时机。环境中的噪声对无线电波的干扰较大，所以对无线电波的信号滤波问题成为研究的重点。早在20世纪80年代，LMS理论就已经被提出。基于这种理论的自适应滤波器算法被广泛应用于通信、故障诊断、雷达引信滤波等领域。然而在收敛性能和稳态特性方面，存在不能同时兼顾的矛盾。为此研究人员对LMS算法进行了改进和优化。汪潮等基于分段的方法，提出了一种变步长数学模型，该模型虽然能够有效缓解这种矛盾，但是增加了算法的复杂度和应用的局限性，导致实用性能很低。Li等、Ao等考虑了迭代过程中的步长与误差的非线性关系，但忽略了相邻步长之间的关系对算法滤波性能的影响。张红梅等虽然改善Li等的不足，但步长算法太复杂，导致计算量非常大，算法的实用性不高。

为了完善上述不足，文中依据LMS原理和反馈控制原理，构建了本次步长和本次误差与前一次误差的比率关系。同时为了避免算法失去迭代性，有必要在迭代的过程中，动态的约束步长的变化。引入一个约束因子，当迭代次数比较小时，该因子几乎不起作用；当迭代次数较大时，该约束因子对步长具有一定的约束作用。最后再将新算法模型应用到无线电引信的滤波处理中，以验证其特性。

自适应滤波器的基本原理如图1所示。

图1 自适应滤波器简图

其中：()为输入信号；()为输出信号；()为与()不相关的输入信号；()为期望信号；()=()-()。图1的滤波器是最常用的FIR数字滤波器。LMS的迭代公式为：

()=()()

(1)

()=()-()

(2)

(+1)=()+2u()()

(3)

式中：为步长因子。

满足算法的收敛条件为：0≤≤1，是()的自相关矩阵最大特征值。

1 自适应滤波算法

变步长的算法模型为：

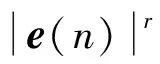
(4)

式中,,均为常量，其最佳取值为：=50,=02,=2。在此算法模型的基础上，引入反馈控制函数和步长函数幅度因子。即当为常数时，将作为跟当前与前一次误差值的比率的平方呈正相关的动态变量；将当是迭代次数成非线性关系的动态变量。其表达式为：

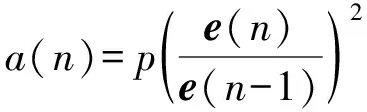
(5)

()=exp()

(6)

改进的步长与误差关系的新模型为：

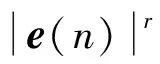
(7)

2 新算法滤波仿真及参数确定

在新算法模型中，共有4个待确定的参数：，，，；自适应滤波器阶数为2。滤波器系数在仿真的过程中具有两个值，开始预设值是=[08 05]，当采样点数为500时，重置预设值=[04 02]。初设采样点数为1 000，独立仿真次数为200次。

2.1 确定参数b对新算法滤波性能的影响

取=100,=0001,=2时,自适应滤波算法的收敛曲线如图2所示。

图2 不同b值的算法收敛曲线

由图2可知：值对滤波性能的影响主要体现在收敛速度上。当=001时，收敛速度慢；当=002时，收敛速度明显加快；当=004时，收敛速度与=002时相比，收敛速度更快。当=008时，收敛速度最快，但是其稳态误差最大。当分别取001，002，004时,曲线的稳态误差基本没有变化。综合考虑，取=004

所谓的外汇资金池，就是可以自由兑换外币经营项目账户和资金账户的管理模式。外汇资金池的构建以委托贷款作为基础，在其作用下，境内企业外汇资金的运用更加便利，外汇资金经营更加高效。

2.2 确定参数f对新算法滤波性能的影响

当=004，=100，=2时，取不同值时，自适应滤波算法的收敛曲线如图3所示。

图3 不同f值的算法收敛曲线

由图可知，当采样点数小于500时，取不同值几乎不影响对收敛曲线的收敛速度和稳态误差。当采样点数大于500时，的取值对收敛曲线的稳态误差和收敛速度都有影响。在稳态误差方面，当分别取-0001，-0002，-0003时，曲线的稳态误差大小基本一样;当=-0004时，曲线的稳态误差明显变大。在收敛速度方面，=-0004时，曲线的收敛速度最慢；当=-0003时，曲线的收敛速度有所加快；当=-0002时，收敛速度明显加快；当=-0001时收敛速度最快。综合考虑曲线的收敛速度和稳态误差，因此取=-0001。

2.3 确定参数p对新算法滤波性能的影响

当=004，=-0001，=2时，取不同值时，自适应滤波算法的收敛曲线如图4所示。

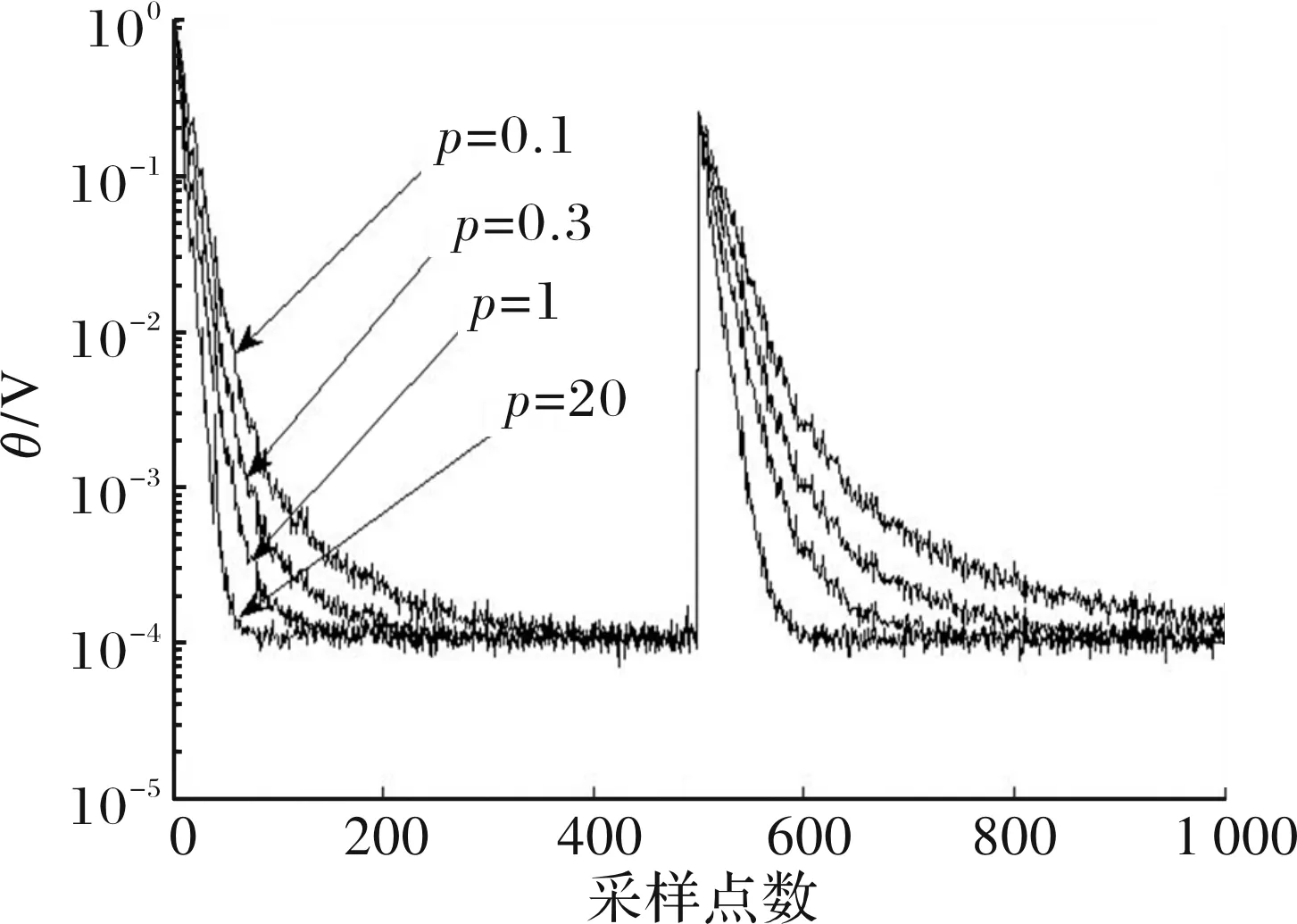
图4 不同p值的算法收敛曲线

由图可知，的取值对收敛曲线稳态误差的影响不明显。当=01时，曲线的收敛速度最慢；当=03时，曲线的收敛速度与=01时相比收敛速有所加快；当=1时，曲线的收敛速度比=03时的更快；当=20时，曲线的收敛速度最快。综合考虑曲线的稳态误差与收敛速度，取=20。

2.4 确定参数r对新算法滤波性能的影响

当=004,=-0001,=20时，取不同值时，自适应滤波算法的收敛曲线如图5所示。

图5 不同r值的算法收敛曲线

由图可知，的取值对收敛曲线的稳态误差和收敛速度的影响较大。在收敛速度方面，当=4时，曲线的收敛速度最慢；当=3时，曲线的收敛速度加快；当=2时，曲线的收敛速度明显加快；=1时，收敛速度最快。在稳态误差方面，当=4时，曲线的稳态误差最大。当=3,=2,=1时，曲线的稳态误差没有明显差别。综合考虑，取=1。

2.5 新算法与文献[11]算法滤波性能对比

由图6可知：与文献[11]算法相比，从收敛速度上可以看出，新算法的收敛性能明显比较好。从稳态误差方面看，新算法的稳态误差值也明显低于文献[11]的。综合以上分析，文中提出的新算法能够有效改善LMS算法滤波性的不足。

图6 算法的收敛曲线对比

3 新算法模型在引信中的应用

对文献[13]中的超宽带无线电引信回波信号进行分析，其时域的数学模型如下：

(8)

式中：为无线电引信的中心频率；为无线电引信的脉冲宽度。为了使得信号在输出时刻近似为零，设置为08。根据实际回波信号的波形特点。设置=2 GHz，=5 ns。仿真结果如图7、图8所示。

图7 文献[11]算法和新算法处理后的回波信号

图8 文献[11]算法与新算法对回波信号的误差性能

由图7可知：在=4 ns时，图7(d)子图更加接近理想信号，图7(c)子图相比于理想信号有明显的失真。新算法滤波的逼真度、滤波性能明显优于文献[11]。

由图8可知：在=2 ns处误差开始产生一次明显的尖峰效果。此时，两种算法产生的尖峰最高点对应的纵坐标值约为：新算法误差约为0.02；文献[11]算法误差约为0.09。即：新算法的抗干扰能力是文献[11]的4.5倍。

4 结论

综合考虑LMS算法的迭代步长与误差的关系，前一次迭代步长与当前迭代步长的关系以及当前步长随着迭代次数的变化情况，提出了一种能够涵盖上述3个因素的数学模型。通过对高斯白噪声和引信滤波信号的实验，验证了文中提出的算法具有较好的稳态特性和收敛特性，极大的改善了LMS算法滤波性能的不足。